
第五章多元线性▣归分析 Chapter 5:Multiple Regression
第五章 多元线性回归分析 Chapter 5: Multiple Regression

很多时候,我们研究的问题是受多个因素影响的, 需要建立多元回归方程,进行多元回归分析: >确定各个自变量对依变量的单独效应和综合效应 >对单独效应和综合效应的显著性进行测验,在自变 量中选择对依变量有显著效应的自变量,建立最优多 元回归方程 >评定各个自变量对依变量的相对重要性,以便抓住 关键因素,分析它们对所研究问题的影响程度
很多时候,我们研究的问题是受多个因素影响的, 需要建立多元回归方程,进行多元回归分析: ➢确定各个自变量对依变量的单独效应和综合效应 ➢对单独效应和综合效应的显著性进行测验,在自变 量中选择对依变量有显著效应的自变量,建立最优多 元回归方程 ➢评定各个自变量对依变量的相对重要性,以便抓住 关键因素,分析它们对所研究问题的影响程度

y =b0+blxl +b2x2+b3x3+.+xmbm 按照最小二乘法,分别对b1、b2、b3、.、bm求偏导, 并令之等于0,建立方程组为: blLl1+b2L12+.+bnLlm Lly b1121+b2122+.+bnL2m L2y bILml+b2Lm2+.+bnLmm=Lby
y = b0+b1x1+b2x2+b3x3+.+ xmbm 按照最小二乘法,分别对b1、b2、b3、.、bm求偏导, 并令之等于0,建立方程组为: + + + = + + + = + + + = b Lm b Lm bnLmm Lby b L b L bnL m L y b L b L bnL m L y 1 1 2 2 . . 1 21 2 22 . 2 2 1 11 2 12 . 1 1

按照矩阵的写法,可将上述方程组写为: L11L12L13.L1m L21L22L23.L2m b2 Lm1 Lm2 Lm3.Lmm bm 个 个 L X B=Y LLB=LY
按照矩阵的写法,可将上述方程组写为: L11 L12 L13 . L1m b1 L1y L21 L22 L23 . L2m b2 L2y Lm1 Lm2 Lm3. Lmm bm Lmy + = L × B=Y L-1LB= L-1Y
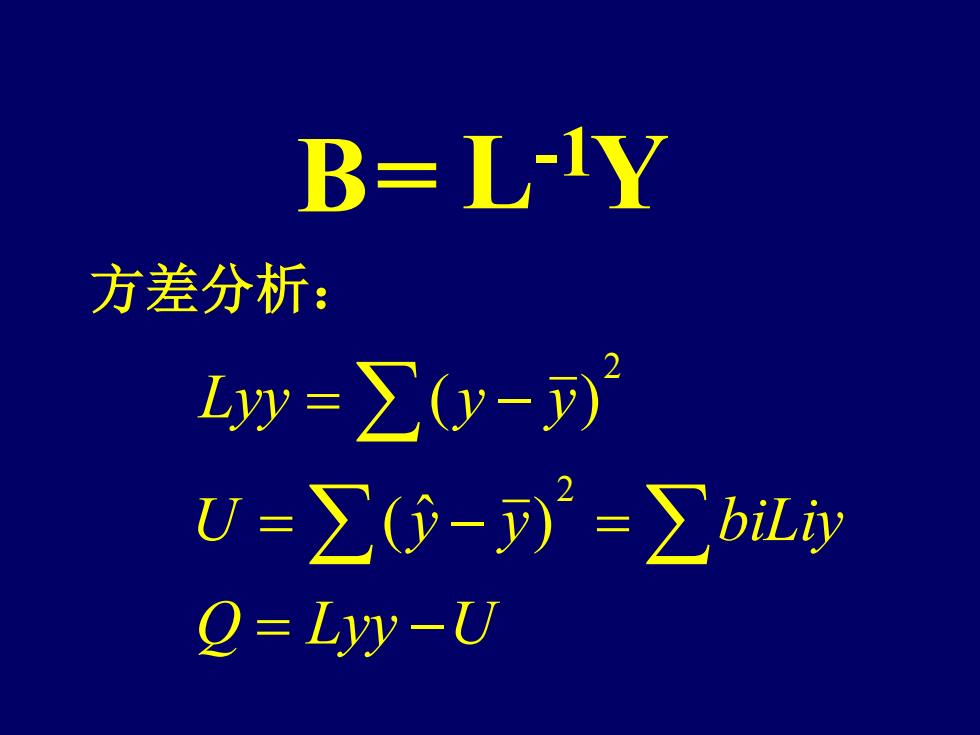
B=L-Y 方差分析: Lw=∑-)1 U=∑(5-)=∑by Q=Lyy-U
B= L-1Y 方差分析: Q Lyy U U y y biLiy Lyy y y = − = − = = − 2 2 ( ˆ ) ( )
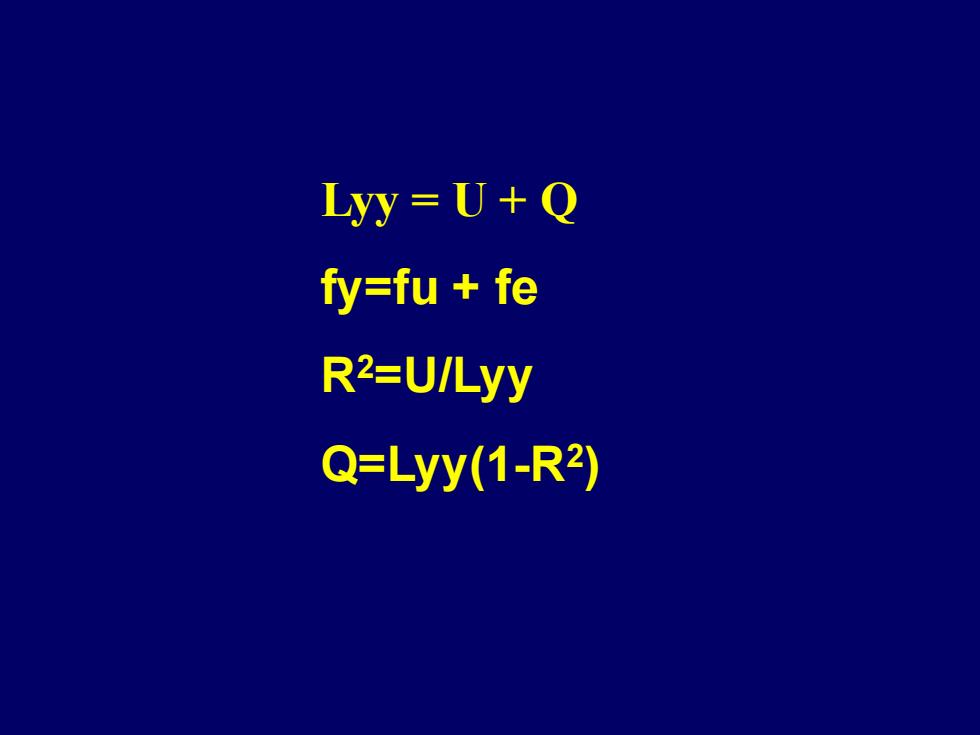
Lyy=U+Q fy=fu fe R2=U/Lyy Q=Lyy(1-R2)
Lyy = U + Q fy=fu + fe R2=U/Lyy Q=Lyy(1-R2 )

方差分析表 Source DF SS MS F Reg m U U/m U/(mS) Res N-m-1Q Q/(N-m-1)=S Total N-1 Lyy
方差分析表 Source DF SS MS F Reg m U U/m U/(mS) Res N-m-1 Q Q/(N-m-1)=S Total N-1 Lyy
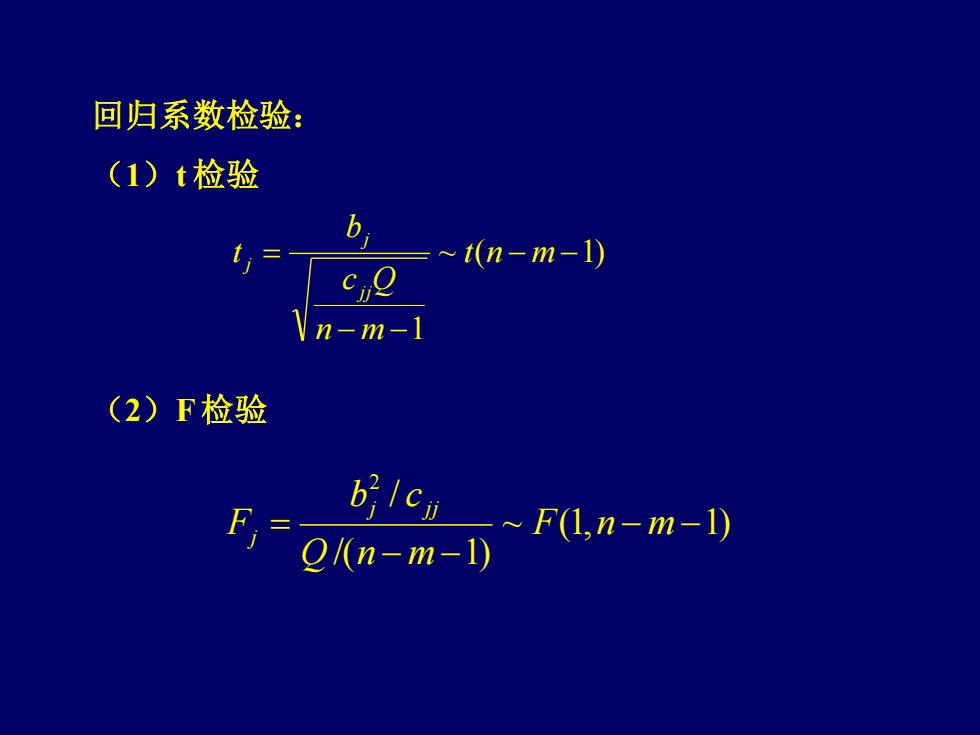
回归系数检验: (1)t检验 b ≈t(n-m-1) n-m- (2)F检验 blcy F,=OK(n-m-1) 。一FL,n-m-1)
回归系数检验: (1)t 检验 (2)F 检验 ~ ( 1) 1 − − − − = t n m n m c Q b t j j j j ~ (1, 1) /( 1) / 2 − − − − = F n m Q n m b c F j j j j

多元相关或称复相关(Multiple Correlation):是在m+1 个变量中,m个变量的综合和一个变量的相关。 偏相关(Partial Correlation):是在其余M一2个变量皆 固定时,指定的两个变量间的相关
多元相关或称复相关(Multiple Correlation):是在m+1 个变量中,m个变量的综合和一个变量的相关。 偏相关(Partial Correlation):是在其余M-2个变量皆 固定时,指定的两个变量间的相关

偏回归系数i不能反映自变量的相对重要性,因为: 1.bi带有具体的单位,单位不同无法比较; 2.即使单位相同,的变异程度不同,也不能比较。 但可以采用标准化的偏回归系数,也称通径系数(Path coefficient): 1/VSS,(n=1) P,=b 1/SS,/(n-1) 即对分子和分母分别除以Y和X的标准差,就可以消除单 位和变异度的影响,其统计学意义是若增加一个标准差单 位,Y将增加或减少P个标准差单位
偏回归系数bi不能反映自变量的相对重要性,因为: 1. bi 带有具体的单位,单位不同无法比较; 2. 即使单位相同,Xi的变异程度不同,也不能比较。 但可以采用标准化的偏回归系数,也称通径系数(Path coefficient): 即对分子和分母分别除以Y和Xi的标准差,就可以消除单 位和变异度的影响,其统计学意义是若增加一个标准差单 位,Y将增加或减少Pi个标准差单位。 y xi i x y i i SS SS b SS n SS n P b = − − = 1/ /( 1) 1/ /( 1)