
第四章样本及抽样分布 。引言un ·随机样本 ·抽样分布
第四 章 样本及抽样分布 l 引言 l 随机样本 l 抽样分布 run

4.1随机样本 一、总体与样本 1.总体:研究对象的全体。 通常指研究对象的某项数量指标。 组成总体的元素称为个体。 从本质上讲,总体就是所研究的随机变量或 随机变量的分布
4.1 随机样本 一 、总体与样本 1. 总体:研究对象的全体。 通常指研究对象的某项数量指标。 组成总体的元素称为个体。 从本质上讲,总体就是所研究的随机变量或 随机变量的分布

2.样本:来自总体的部分个体X1,.,Xm 如果满足: (1)同分布性:X, 如何抽样】 i=1,.,n与总体同分布. (2)独立性: 桶内装有总体 X1,.,X相互独立; 的所有个体 则称为容量为n的简单随 机样本,简称样本。 而称X,.,X的一次 实现为样本观察值,记为
2. 样本:来自总体的部分个体X1, . ,Xn 如果满足: (1)同分布性: Xi, i=1,.,n与总体同分布. (2)独立性: X1,. ,Xn 相互独立; 则称为容量为n 的简单随 机样本,简称样本。 而称X1,. ,Xn 的一次 实现为样本观察值,记为 x1,. ,xn

来自总体X的随机样本X1,.,Xn可记为 iid X1,.,Xn~X或f(x),F(x)2. 显然,样本联合分布函数或密度函数为 F(x1,x2,.,xn)=ΠF(x,) =1 或∫(x1,x2,.,xn)=门f(x,)
来自总体X的随机样本X1, . ,Xn可记为 , , ~ ( ), ( ),. 1 X X X f x F x iid n 或 显然,样本联合分布函数或密度函数为 n i n i F x x x F x 1 1 2 * ( , , , ) ( ) 或 n i n i f x x x f x 1 1 2 * ( , , , ) ( )
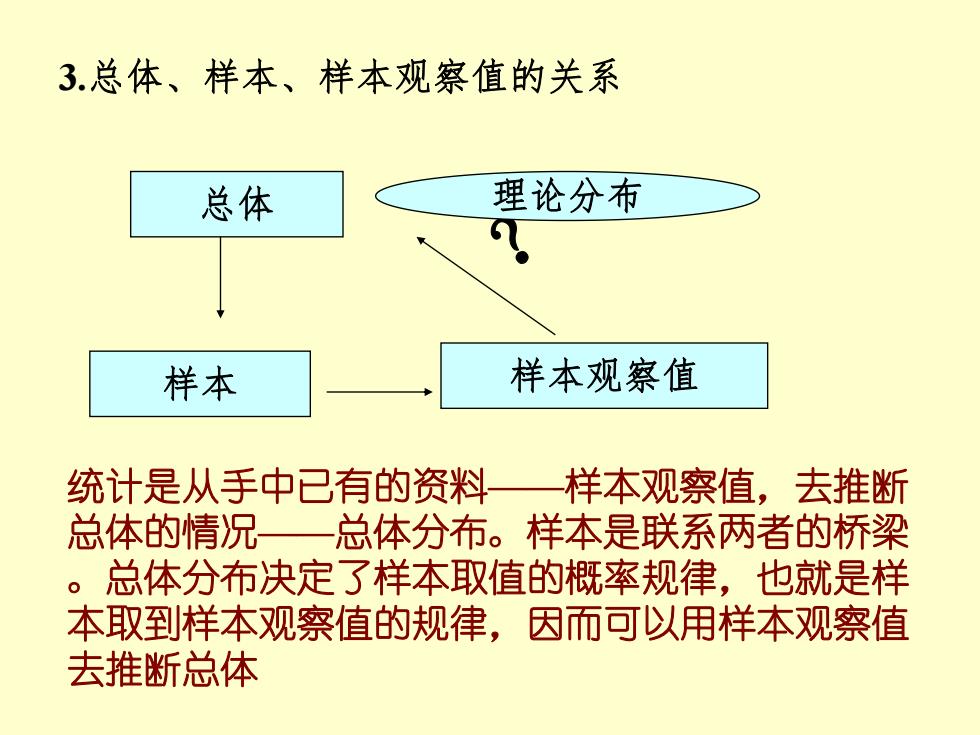
3.总体、样本、样本观察值的关系 总体 理论分布 0。 样本 样本观察值 统计是从手中已有的资料一样本观察值,去推断 总体的情况一总体分布。样本是联系两者的桥梁 。总体分布决定了样本取值的概率规律,也就是样 本取到样本观察值的规律,因而可以用样本观察值 去推断总体
3.总体、样本、样本观察值的关系 总体 样本 样本观察值 理论分布 统计是从手中已有的资料——样本观察值,去推断 总体的情况——总体分布。样本是联系两者的桥梁 。总体分布决定了样本取值的概率规律,也就是样 本取到样本观察值的规律,因而可以用样本观察值 去推断总体

二、统计量 定义:称样本X,.,Xn的函数 g(X1,.,Xn)是总体X的一个统计量,如果 g(X1,.,Xn)不含未知参数 几个常用的统计量: 1样本均值X=1之X n i= 2样本方差s2=1x-x n-li 样本均方差(标准差)S=VS2
二、统计量 定义:称样本X1, . ,Xn的函数 g(X1, . ,Xn )是总体X的一个统计量,如果 g(X1, . ,Xn )不含 未知 参数 , 1 1. 1 n i Xi n 样本均值 X ( ) , ( ) 1 1 2. 2 1 2 2 S S X X n S n i i 样本均方差 标准差 样本方差 几个常用的统计量 :

3样本k阶矩 原点矩= n i=l 中心矩B=1x,-万 i
n i k i k n i k i k X X n B X n A 1 1 ( ) , 1 1 中心矩 原点矩 3.样本k阶矩

4.2抽样分布 统计量的分布称为抽样分布。数理统 计中常用到如下三个分布: X2一分布、t一分布和F一分布。 一、 x2一分布 iid 1.构造 设X,.,X.N0,),则x2=∑X?x2(m) 称为自由度为n的x2-分布
4.2 抽样分布 一 、 2—分布 统计量的分布称为抽样分布。数理统 计中常用到如下三个分布: 2—分布、 t —分布和F—分布。 . 1. , , ~ (0,1), ~ ( ). 2 2 1 2 2 1 称为自由度为 的 分布 构造 设 则 n X X N X n n i i iid n

2.x2一分布的密度函数fy)曲线 -1-y 0, y≤0 0.4 0.35 2=1 0.3 0.25 0.2 2=4 0.15 22=10 0.1 2=20 0.05 10 20 30
2.2—分布的密度函数f(y)曲线 0, y 0 y e , y 0 f(y) 2 y 1 2 n 2 (n / 2) 1 n / 2
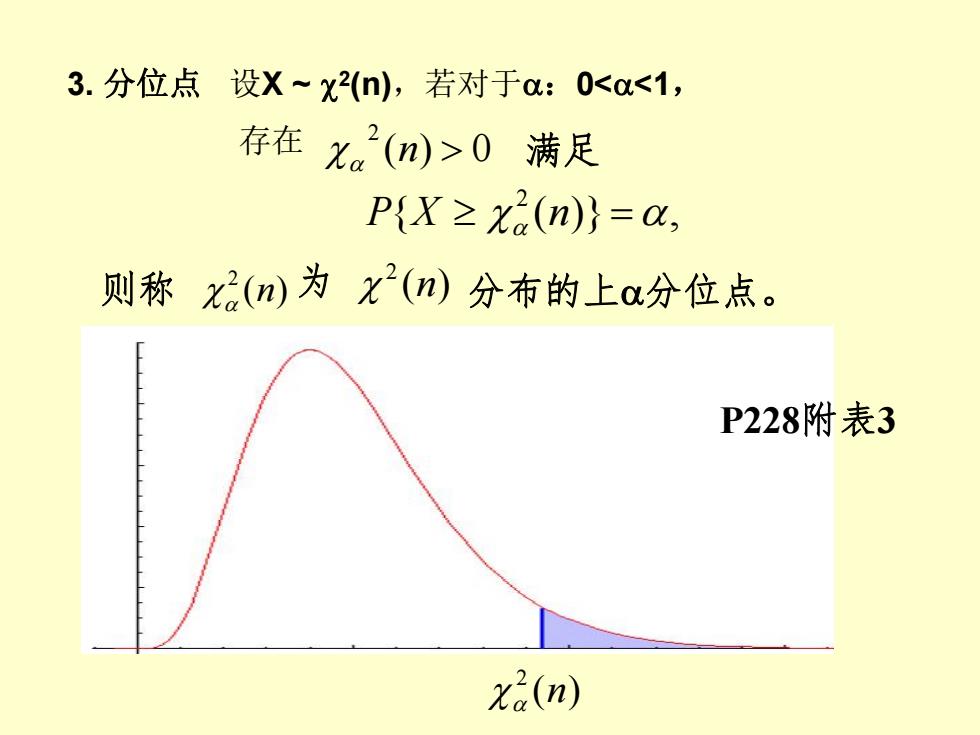
3.分位点设X~x2n),若对于:00满足 P{X≥x2(n)}=&, 则称x(n)为Y(n)分布的上ou分位点。 P228附表3 x(n)
3. 分位点 设X ~ 2(n),若对于:0<<1, 存在 ( ) 0 2 n 满足 { ( )} , 2 P X n 则称 ( ) 2 n 为 ( ) 2 n 分布的上分位点。 ( ) 2 n P228附表3