
概率论是研究什么的? 随机现象:不确定性与统计规律性 概率论 —研究和示随机现象 的统计规律性的科学
序 言 概率论是研究什么的? 随机现象:不确定性与统计规律性 概率论——研究和揭示随机现象 的统计规律性的科学

第一章随机事件及其概率 。随机事件及其运算 概率的定义及其运算 $条件概率 事件的独立性
第一章 随机事件及其概率 随机事件及其运算 概率的定义及其运算 条件概率 事件的独立性

1.1随机事件及其概率 一、随机试验(简称“试验”) 随机试验的特点(p2) 1.可在相同条件下重复进行; 2.试验可能结果不止一个,但能确定所有的可能结果; 3.一次试验之前无法确定具体是哪种结果出现。 随机试验可表为E
1.1随机事件及其概率 一、随机试验(简称“试验”) 随机试验的特点(p2) 1.可在相同条件下重复进行; 2.试验可能结果不止一个,但能确定所有的可能结果; 3.一次试验之前无法确定具体是哪种结果出现。 随机试验可表为E

随机实验的例 E1:抛一枚硬币,分别用“H”和“T”表示出正面和反面; E2:将一枚硬币连抛三次,考虑正反面出现的情况; E,将一枚硬币连抛三次,考虑正面出现的次数; E4掷一颗骰子,考虑可能出现的点数; E5:记录某网站一分钟内受到的点击次数; E6在一批灯泡中任取一只,测其寿命; E:任选一人,记录他的身高和体重。 随机事件
E1 : 抛一枚硬币,分别用“H” 和“T” 表示出正面和反面; E2 : 将一枚硬币连抛三次,考虑正反面出现的情况; E3 :将一枚硬币连抛三次,考虑正面出现的次数; E4 :掷一颗骰子,考虑可能出现的点数; E5 : 记录某网站一分钟内受到的点击次数; E6 :在一批灯泡中任取一只,测其寿命; E7 :任选一人,记录他的身高和体重 。 随机实验的例 随机事件

二、样本空间(p2) 1、样本空间:实验的所有可能结果所组成的 集合称为样本空间,记为S={e}; 2、样本点:试验的每一个结果或样本空间的 元素称为一个样本点,记为e. 3由一个样本点组成的单点集称为一个基本事 件,也记为e %拾出E1-E7的样幸空间 幻灯片6
二、样本空间(p2) 1、样本空间:实验的所有可能结果所组成的 集合称为样本空间,记为S={e}; 2、样本点: 试验的每一个结果或样本空间的 元素称为一个样本点,记为e. 3.由一个样本点组成的单点集称为一个基本事 件,也记为e. EX 给出E1-E7的样本空间 幻灯片 6

随机事件 1.定义(p3定义1.1.2)试验中可能出现或可能不出现的情 况叫“随机事件”,简称"事件”记作A、B、C等 任何事件均可表示为样本空间的某个子集, 称事件A发生当且仅当试验的结果是子集A中的元素 2.两个特殊事件:必然事件S、不可能事件φ.(p3) 例如对于试验E,以下A、B、C即为三个随机事件: A=“至少出一个正面” =HHH,HHT,HTH,THH,HTT,THT,TTH; B=“两次出现同一面”={HHH,TTT} C=恰好出现一次正面”={HTT,THT,TTH} 再如,试验E6中D=“灯泡寿命超过1000小时” ={x:1000<x<T(小时)}
随机事件 1.定义 (p3定义1.1.2) 试验中可能出现或可能不出现的情 况叫“随机事件”, 简称“事件”.记作A、B、C等 任何事件均可表示为样本空间的某个子集. 称事件A发生当且仅当试验的结果是子集A中的元素 2.两个特殊事件: 必然事件S 、不可能事件.(p3) 例如 对于试验E2,以下A 、 B、C即为三个随机事件: A=“至少出一个正面” ={HHH, HHT, HTH, THH,HTT,THT,TTH}; B=“两次出现同一面”={HHH,TTT} C=“恰好出现一次正面”={HTT,THT,TTH} 再如,试验E6中D=“灯泡寿命超过1000小时” ={x:1000<x<T(小时)}

可见,可以用文字表示事件,也可以将事件表示为样本空 间的子集,后者反映了事件的实质,且更便于今后计算概 率 还应注意,同一样本空间中,不同的事件之间有一定的关 系,如试验邻,当试验的结果是HHH时,可以说事件A和B 同时发生了,但事件B和C在任何情况下均不可能同时发生 。易见,事件之间的关系是由他们所包含的样本点所决定 的,这种关系可以用集合之间的关系来描述。 三、事件之间的关系
三、事件之间的关系 可见,可以用文字表示事件,也可以将事件表示为样本空 间的子集,后者反映了事件的实质,且更便于今后计算概 率 还应注意,同一样本空间中,不同的事件之间有一定的关 系,如试验E2,当试验的结果是HHH时,可以说事件A和B 同时发生了;但事件B和C在任何情况下均不可能同时发生 。易见,事件之间的关系是由他们所包含的样本点所决定 的,这种关系可以用集合之间的关系来描述
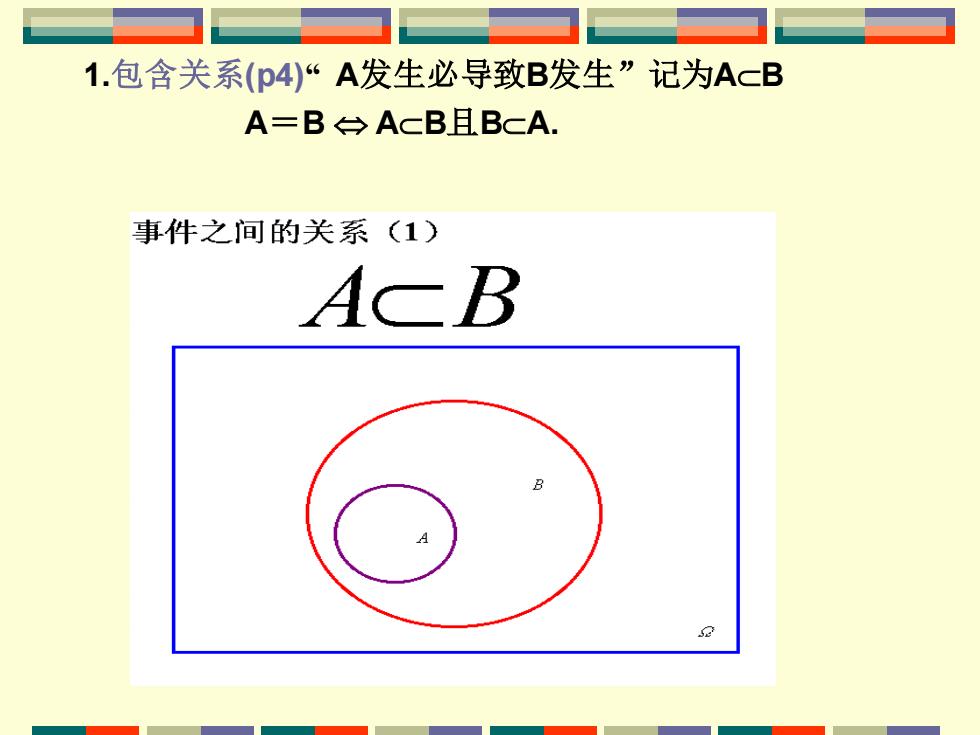
1.包含关系(p4)“A发生必导致B发生”记为AcB A=B台ACB且BCA. 事件之间的关系(1) ACB
1.包含关系(p4)“ A发生必导致B发生”记为AB A=B AB且BA
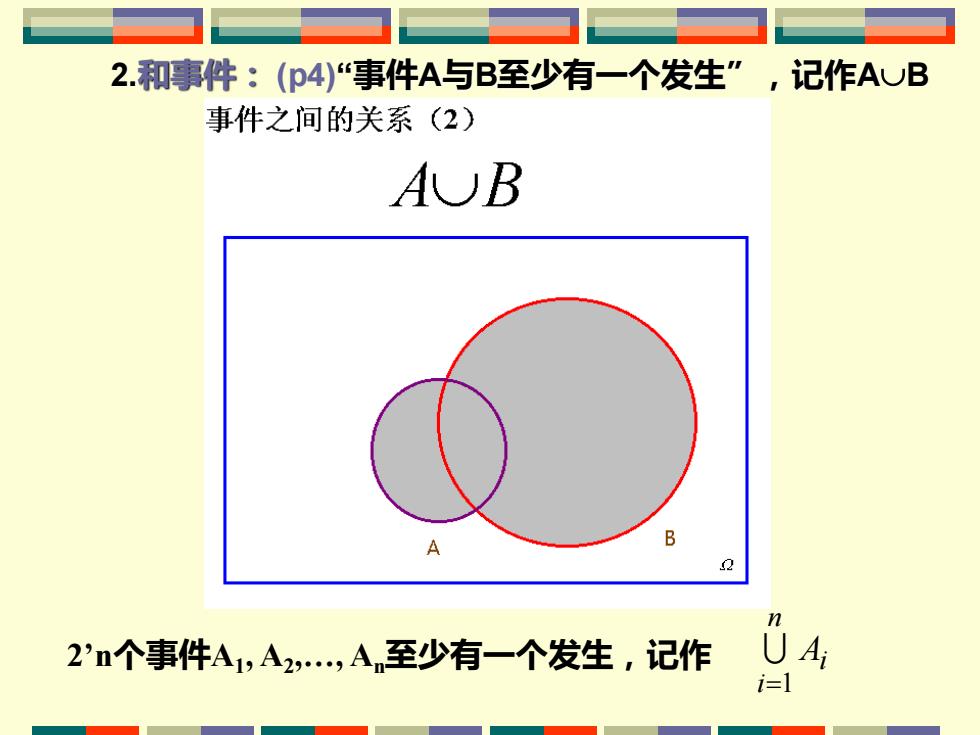
2.和事件:(p4)事件A与B至少有一个发生”,记作AUB 事件之间的关系(2) AUB B 2 n 2'n个事件A1,A2,A至少有一个发生,记作 i=l
2.和事件: (p4)“事件A与B至少有一个发生”,记作AB 2’n个事件A1 , A2 ,., An至少有一个发生,记作 i n i A =1
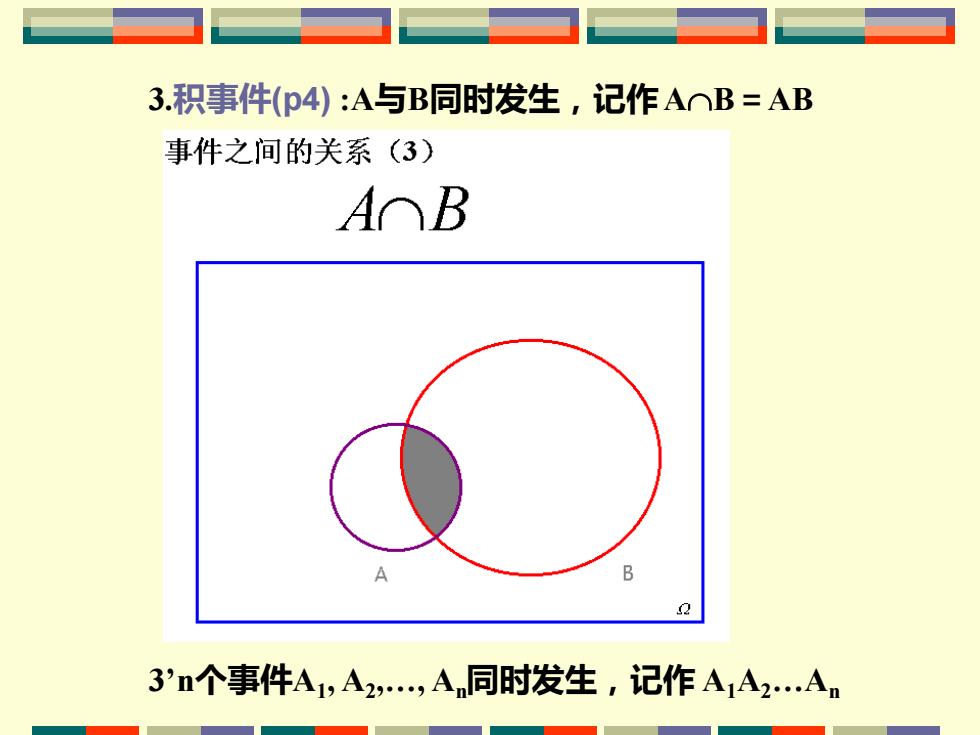
3.积事件(p4):A与B同时发生,记作A⌒B=AB 事件之间的关系(3) A⌒B B 2 3'n个事件A1,A2,A同时发生,记作A1A2An
3.积事件(p4) :A与B同时发生,记作AB=AB 3’n个事件A1 , A2 ,., An同时发生,记作 A1A2.An