
从本章开始,介绍一些常用的假设检验方法。 第5章:对单个和两个平均数的假设检验 第6、7章:方差分析
从本章开始,介绍一些常用的假设检验方法。 第5章:对单个和两个平均数的假设检验 第6、7章:方差分析

假设检验的基本步骤: 1、提出假设 H0:原假设或零假设,被直接检验的假设,否定 或接受 HA:备择假设,一旦否定原假设就接受备择假设 2、计算统计量 利用原假设所提供的信息,而且其抽样分布已知
假设检验的基本步骤: 1、提出假设 H0:原假设或零假设,被直接检验的假设,否定 或接受 HA:备择假设,一旦否定原假设就接受备择假设 2、计算统计量 利用原假设所提供的信息,而且其抽样分布已知
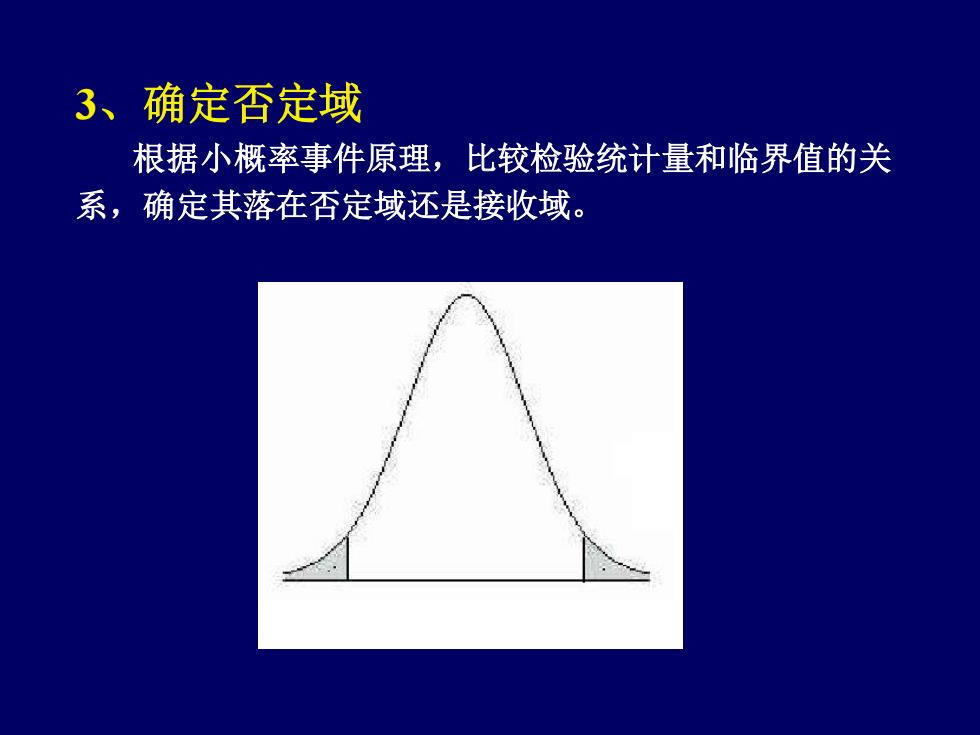
3、确定否定域 根据小概率事件原理,比较检验统计量和临界值的关 系,确定其落在否定域还是接收域
3、确定否定域 根据小概率事件原理,比较检验统计量和临界值的关 系,确定其落在否定域还是接收域

4、对假设进行统计推断 显著水平:0.01;0.05 (1)差异不显著:接受原假设 (2)差异显著:在 0.05 水平下,否定原假设, 接受备择假设 (3)差异极显著:在 0.01 水平下,否定原假 设,接受备择假设
4、对假设进行统计推断 显著水平:0.01;0.05 (1)差异不显著:接受原假设 (2)差异显著:在 0.05 水平下,否定原假设, 接受备择假设 (3)差异极显著:在 0.01 水平下,否定原假 设,接受备择假设
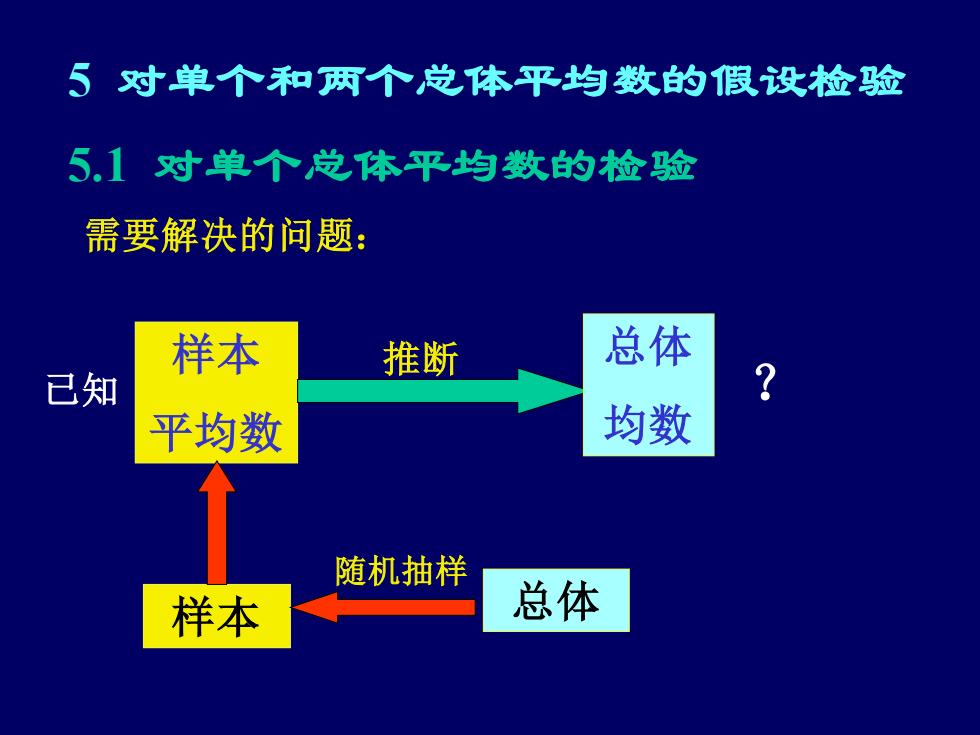
5 对单个和两个总体平均数的假设检验 需要解决的问题: 5.1 对单个总体平均数的检验 样本 平均数 总体 均数 推断 已知 ? 样本 随机抽样 总体
5 对单个和两个总体平均数的假设检验 需要解决的问题: 5.1 对单个总体平均数的检验 样本 平均数 总体 均数 推断 已知 ? 样本 随机抽样 总体

5.1.1 Z检验-总体的方差σ 2 已知 利用 Z 统计量进行检验,Z统计量服从标准正态 分布,因而称为Z检验。 检验步骤如下: 1、提出假设:针对不同的具体情况,有3中假设。 (1) H0:μ=μ0;HA:μ≠μ0 双侧检验 (2) H0:μ=μ0;HA:μ μ0 单侧检验
5.1.1 Z检验-总体的方差σ 2 已知 利用 Z 统计量进行检验,Z统计量服从标准正态 分布,因而称为Z检验。 检验步骤如下: 1、提出假设:针对不同的具体情况,有3中假设。 (1) H0:μ=μ0;HA:μ≠μ0 双侧检验 (2) H0:μ=μ0;HA:μ μ0 单侧检验

2、计算统计量Z 5.1.1 Z检验-总体的方差σ 2 已知 ( ,) :样本含量; :总体标准差 :样本平均数; ~ 0 1 0 Z N n X n X X Z X − = − =
2、计算统计量Z 5.1.1 Z检验-总体的方差σ 2 已知 ( ,) :样本含量; :总体标准差 :样本平均数; ~ 0 1 0 Z N n X n X X Z X − = − =

5.1.1 Z检验-总体的方差σ 2 已知 3、确定否定域并做统计推断 对于给定的显著性水平,针对3种不同的假设, 原假设的否定域分别为: a a a Z Z Z 2 2 3 2 1 − ( ) ( ) () μa 和μ2a:分别为标准正态分布 两尾概率为a和2a时 的分位点。 见附表2。a=0.05时,μa =1.96 μ2a=1.64 a=0.01时,μa =2.58 μ2a=2.33
5.1.1 Z检验-总体的方差σ 2 已知 3、确定否定域并做统计推断 对于给定的显著性水平,针对3种不同的假设, 原假设的否定域分别为: a a a Z Z Z 2 2 3 2 1 − ( ) ( ) () μa 和μ2a:分别为标准正态分布 两尾概率为a和2a时 的分位点。 见附表2。a=0.05时,μa =1.96 μ2a=1.64 a=0.01时,μa =2.58 μ2a=2.33

5.1.2 t 检验-总体的方差σ 2未知 在实际情况下,总体方差 σ 2 一般是未知的,因 此无法计算Z 统计量,不能采用Z 检验。 这时,用样本方差 S 2 代替总体方差。 ( ) :样本含量; :样本标准差 :样本平均数; ~ 1 0 − − = − = t t n n S X n S X S X t X
5.1.2 t 检验-总体的方差σ 2未知 在实际情况下,总体方差 σ 2 一般是未知的,因 此无法计算Z 统计量,不能采用Z 检验。 这时,用样本方差 S 2 代替总体方差。 ( ) :样本含量; :样本标准差 :样本平均数; ~ 1 0 − − = − = t t n n S X n S X S X t X
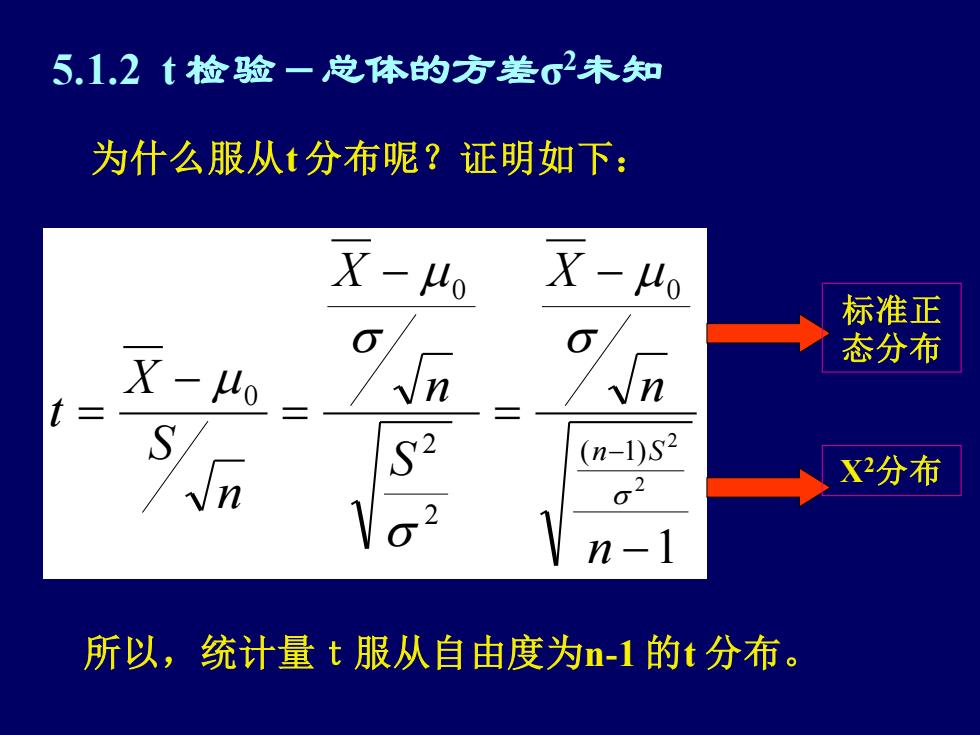
1 2 2 ( 1) 0 2 2 0 0 − − = − = − = − n n X S n X n S X t n S 5.1.2 t 检验-总体的方差σ 2未知 为什么服从t 分布呢?证明如下: 标准正 态分布 Χ2分布 所以,统计量t服从自由度为n-1 的t 分布
1 2 2 ( 1) 0 2 2 0 0 − − = − = − = − n n X S n X n S X t n S 5.1.2 t 检验-总体的方差σ 2未知 为什么服从t 分布呢?证明如下: 标准正 态分布 Χ2分布 所以,统计量t服从自由度为n-1 的t 分布