
第三章随机变量的数字特征 4随机变量的数学期望 随机变量的方差 随机变量的协方差和相关条数 大数定律 中心极限定理
第三章 随机变量的数字特征 随机变量的数学期望 随机变量的方差 随机变量的协方差和相关系数 大数定律 中心极限定理

3.1数学期望 一.数学期望的定义 数学期望—描述随机变量取值的平均特征 例1设某班40名学生的概率统计成绩及得分 人数如下表所示: 分数 140 6070 80 90 100 人数 1 6 9 15 7 2 则学生的平均成绩是总分÷总人数(分)。即 1×40+6×60+9×70+15×80+7×90+2×100 =76.5分) 1+6+9+15+7+2
3.1数学期望 一.数学期望的定义 例1 设某班40名学生的概率统计成绩及得分 人数如下表所示: 分数 40 60 70 80 90 100 人数 1 6 9 15 7 2 则学生的平均成绩是总分÷总人数(分)。即 76.5( ) 1 6 9 15 7 2 1 40 6 60 9 70 15 80 7 90 2 100 = 分 + + + + + + + + + + 数学期望——描述随机变量取值的平均特征

定义1.若X~P{X=k=pk,k=1,2,.n,则称 E(X)=∑xkP k=1 为r.v.X的数学期望,简称期望或均值。 定义2.(p73)若X~P{X=Xk}=pk,k=1,2,.,且 00 ∑xP<0,则称 k= ●● E(X)=∑xPk k=1 为r.v.X的数学期望
定义 1. 若X~P{X=xk }=pk , k=1,2,.n, 则称 =1 | | k k pk x = = n k k pk E X x 1 ( ) 定义 2. (p73)若X~P{X=xk }=pk , k=1,2,.,且 为r.v.X的数学期望,简称期望或均值。 ,则称 ( ) . 1 = = k k pk E X x 为r.v.X的数学期望

例2掷一颗均匀的骰子,以X表示掷得的点数,求X 的数学期望。 定义3若X-fx,o<x<o,|x|f(x)d<o 则称 E(X)=[xf(x)dx. 为X的数学期望。P(74)
例2 掷一颗均匀的骰子,以X表示掷得的点数,求X 的数学期望。 2 7 6 1 ( ) 6 1 = = i= E X k 定义 3 若X~f(x), -<x<, − E(X) = xf(x)dx. − | x | f (x)dx 为X的数学期望。P(74) 则称

例3.若随机变量X服从拉普拉斯分布,其密度函数为 试求EX). 麻-益 令- epk油-=A 00
例3. 若随机变量X服从拉普拉斯分布,其密度函数为 试求E(X). − = − x f x exp 2 1 ( ) 解 dx x x E X − = − − exp 2 ( ) t dt t x t exp | | 2 − + = − − 令 = = − = exp t dt 0

二.几个重要rv.的期望 1.0-1分布的数学期望 0 Pp 1-p → EX=p 2.二项分布B(n,p) P{X==Cp(1-p)”-R k=0.1,.n )-o
二.几个重要r.v.的期望 1.0-1分布的数学期望 P p − p X 1 1 0 EX=p 2. 二项分布B(n, p) = − − − = n k k n k p p k n k n E X k 1 (1 ) !( )! ! ( ) P X k C p p k n k k n k n { = } = (1− ) = 0.1,. −
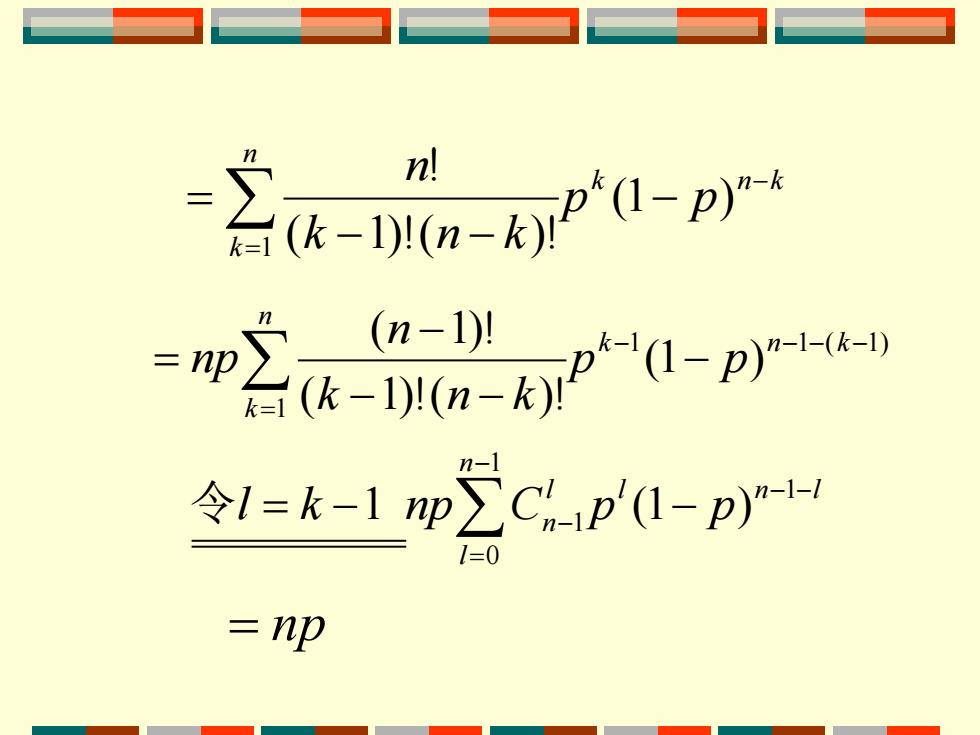
三-内p产 nl =w空a- 令1=k-1p∑Cgp(0-p)H np
k n k n k p p k n k n − = − − − = (1 ) ( 1)!( )! ! 1 1 1 ( 1) 1 (1 ) ( 1)!( )! ( 1)! − − − − = − − − − = k n k n k p p k n k n np= np l n l n l l l k np Cn p p − − − = = − − − 1 1 0 1 令 1 (1 )

3.泊松分布 X-PX=k= 2e,k=0,1,2, n- =, k-0 4.均匀分布U(a,b) 1 &aBa守 a<x<b, 0, 其他 x)-6“生
3.泊松分布 , 0, 1, 2, . ! ~ { = } = = − e k k X P X k k 4. 均匀分布U(a, b) = − 0, , , , 1 ~ ( ) 其他 a x b X f x b a = = − − − = − = = 0 1 1 ; ! ( 1)! ( ) k k k k k e e k E X k + = − = b a a b dx b a x E X ; 2 ( )

5.指数分布 x>0 x≤0 P E(X)=jxie=-jxde和 -xefe
5.指数分布 = − 0 0 0 ( ) x e x f x x 1 = E X x e dx x − = 0 ( ) − = − 0 x xde x e e dx x x − − = − + 0 0

6.正态分布N(,σ) X~f(x)= 1 ,-0<X<0 /2元 -(x-4)2 2o2 dx o =u
6. 正态分布N(, 2 ) − = − − e , x 2 1 X ~ f(x) 2 2 2 (x ) e dx x E X x 2 2 2 ( ) 2 ( ) − − − = ; 2 2 2 e dt x t t t − − − + 令 = =