
第二章随机变量 离散型随机变量 随机变量的分布函数 连续型随机变量 一维随机变量函数的分布 号二维随机变量的联合分布 多维随机变量的边缘分布与独立性 号条件分布 “多维随机变量函数的分布
第二章随机变量 离散型随机变量 随机变量的分布函数 连续型随机变量 一维随机变量函数的分布 二维随机变量的联合分布 多维随机变量的边缘分布与独立性 条件分布 多维随机变量函数的分布

关于随机变量及向量的研究,是概率论的 中心内容.这是因为,对于一个随机试验,我 们所关心的往往是与所研究的特定问题有关的 某个或某些量,而这些量就是随机变量。也可 以说:随机事件是从静态的观点来研究随机现 象,而随机变量则是一种动态的观点,一如数 学分析中的常量与变量的区分那样.变量概念 是高等数学有别于初等数学的基础概念.同样, 概率论能从计算一些孤立事件的概念发展为一 个更高的理论体系,其基础概念是 随机变量
关于随机变量(及向量)的研究,是概率论的 中心内容.这是因为,对于一个随机试验,我 们所关心的往往是与所研究的特定问题有关的 某个或某些量,而这些量就是随机变量.也可 以说:随机事件是从静态的观点来研究随机现 象,而随机变量则是一种动态的观点,一如数 学分析中的常量与变量的区分那样.变量概念 是高等数学有别于初等数学的基础概念.同样, 概率论能从计算一些孤立事件的概念发展为一 个更高的理论体系,其基础概念是 随机变量

2.1随机变量的概念 (p24)定义.设S={e}是试验的样本空 间,如果量X是定义在$上的一个单 A(e 值实值函数即对于每一个e∈S,有一 实数X=X(e)与之对应,则称X为随机 变量。 随机变量常用X、Y、Z或、 等表示。 随机变量的特点: 1X的全部可能取值是互斥且完备的 2X的部分可能取值描述随机事件
2.1随机变量的概念 (p24)定义. 设S={e}是试验的样本空 间,如果量X是定义在S上的一个单 值实值函数即对于每一个eS,有一 实数X=X(e)与之对应,则称X为随机 变量。 随机变量常用X、Y、Z 或 、、 等表示。 随机变量的特点: 1 X的全部可能取值是互斥且完备的 2 X的部分可能取值描述随机事件

7 请举几个实际中随机变量的例子 EX.引入适当的随机变量描述下列事件: ①将3个球随机地放入三个格子中, 事件A={有1个空格},B={有2个空格}, C={全有球}。 ②进行5次试验,事件D={试验成功一次}, F={试验至少成功一次},G={至多成功3次}
EX.引入适当的随机变量描述下列事件: ①将3个球随机地放入三个格子中, 事件A={有1个空格},B={有2个空格}, C={全有球}。 ②进行5次试验,事件D={试验成功一次}, F={试验至少成功一次},G={至多成功3次}
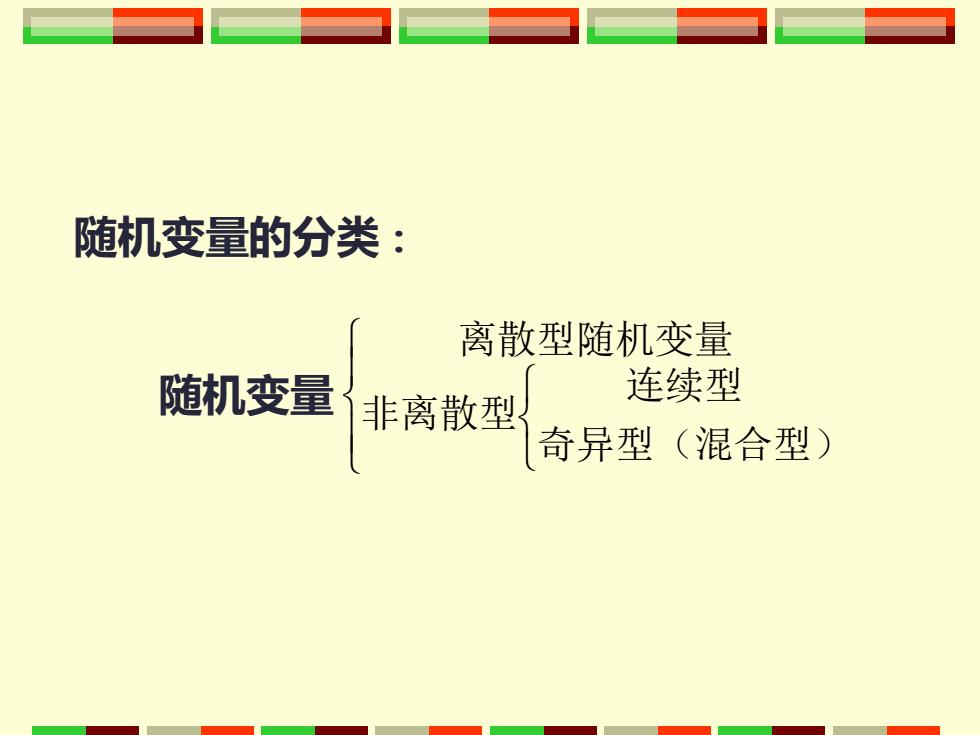
随机变量的分类: 离散型随机变量 随机变量 连续型 非离散型 奇异型(混合型)
奇异型(混合型) 连续型 非离散型 离散型随机变量 随机变量的分类: 随机变量

2.2离散型随机变量 (P25)定义若随机变量X取值x1,X2,X,. 且取这些值的概率依次为P1,P2,P,.,则称 X为离散型随机变量,而称 P{X=X}=Pk,(k=1,2,.) 为X的分布律或概率分布。可表为 X~P{X=xk}=pk,(k=1,2,.), 或. X X1 X2 XK X~ Pk p2
2.2离散型随机变量 (P25)定义 若随机变量X取值x1 , x2 , ., xn , . 且取这些值的概率依次为p1 , p2 , ., pn , ., 则称 X为离散型随机变量,而称 P{X=xk }=pk , (k=1, 2, . ) 为X的分布律或概率分布。可表为 X~ P{X=xk }=pk , (k=1, 2, . ), 或. X ~ X x1 x2 . xK . Pk p1 p2 . pk

2.分布律的性质 (1)pk≥0,k=1,2,.; (2) ∑P1. k> 例1设袋中有5只球,其中有2只白3只黑。】 现从 中任取3只球(不放回),求抽得的白球数X为k的 概率。 解k可取值0,1,2 P{X==
(1) pk 0, k=1, 2, . ; (2) 1 1. k pk = { } . 3 5 3 2 3 C C C P X k k −k = = 例1 设袋中有5只球,其中有2只白3只黑。现从 中任取3只球(不放回),求抽得的白球数X为k的 概率。 解 k可取值0,1,2 2. 分布律的性质

例2.某射手对目标独立射击5次,每次命中目标的概 率为p,以X表示命中目标的次数,求X的分布律。 解:设A一第i次射击时命中目标,i=1,2,3,4,5 则A1,A2.A5,相互独立且 P(A)=p,i=1,2,.5.Sx={0,1,2,3,4,5} PX=0}=P(A1A2A3A4A5)=(1-p)5 P{X=1}=P{4A2A3A4A5UA1A2A3A4A5U.=5p(1-p)4 P{X=2}=P4142A3A4A5UA1A243A4A5U.=C3P2(1-P) P(X=k)=Cp(1-p) k=0,12,5
例2.某射手对目标独立射击5次,每次命中目标的概 率为p,以X表示命中目标的次数,求X的分布律。 解:设Ai⎯第i次射击时命中目标,i=1,2,3,4,5 则A1 ,A2,.A5,相互独立且 P(Ai )=p,i=1,2,.5. SX={0,1,2,3,4,5}, (1-p)5 P{X = 0} = P(A1 A2 A3 A4 A5 ) = { 1} { 3 4 5 . P X = = P A1 A2 A3 A4 A5 A1A2 A A A 4 = 5p(1− p) { } (1 ) 0,1,.,5 5 = = 5 − = − P X k C p p k k k k P{X = 2} = P{A1 A2 A3 A4 A5 A1 A2A3 A4 A5 . = 2 2 3 5 C P (1− P)

“几个常用的离散型分布 (一)贝努里Bernoulli概型与二项分布 1.(0-1)分布(p26) 若以X表示进行一次试验事件A发生的次数,则称 X服从(0-1)分布(两点分布) X~PX=k3=pk(1-p)1-k,(0<p<1)k=0,1 或 X Pk p 1-p
·几个常用的离散型分布 (一)贝努里(Bernoulli)概型与二项分布 1. (0-1)分布(p26) 若以X表示进行一次试验事件A发生的次数,则称 X服从(0-1)分布(两点分布) X~P{X=k}=pk (1-p)1-k , (0<p<1) k=0,1 或 X k p 1 0 p 1− p

2.(p27)定义设将试验独立重复进行n次,每次试 验中,事件A发生的概率均为p,则称这n次试验 为n重贝努里试验. (P27)若以X表示n重贝努里试验事件A发生的次 数,则称X服从参数为np的二项分布。 记作X~B(np) ,其分布律为: P{X=k}=Cp*(I-p)”-k,(k=0,1,n)
(P27)若以X表示n重贝努里试验事件A发生的次 数,则称X服从参数为n,p的二项分布。 记作X~B(n,p) ,其分布律为: 2.(p27)定义 设将试验独立重复进行n次,每次试 验中,事件A发生的概率均为p,则称这n次试验 为n重贝努里试验. P{X k} p (1 p) ,(k 0,1,.,n) k n k k Cn = = − = −