
第三节平均数的假设检验 Hypothesis Testing for Mean M、t Distribution 2、单个样本平均数的假设测验 3、两个样本平均数相比较的假设测验
第三节 平均数的假设检验 Hypothesis Testing for Mean 1、t Distribution 2、单个样本平均数的假设测验 3、两个样本平均数相比较的假设测验

l、t Distribution t分布是W.S.Gosset于1908年首先提出的, 又称为学生氏分布(Studentstdistribution)。它是 一组对称的密度函数,具有一个单独参数 v(自由度)的特定分布。 t分布条件:样本容量不太大(n<30),且 02为未知
1、t Distribution t 分布是W. S. Gosset于1908年首先提出的, 又称为学生氏分布(Student`s t distribution)。它是 一组对称的密度函数,具有一个单独参数 ν(自由度)的特定分布。 t 分布条件:样本容量不太大(n<30),且 σ2为未知

条件:当样本容量不太大(30),t分布趋向于正态分布。 当v0时,与正态分布重合
条件:当样本容量不太大(n30),t 分布趋向于正态分布。 当v→∞时,与正态分布重合。 式中,S 为样本标准差,n 为样本容量。 x x u ( − ) = 正态分布
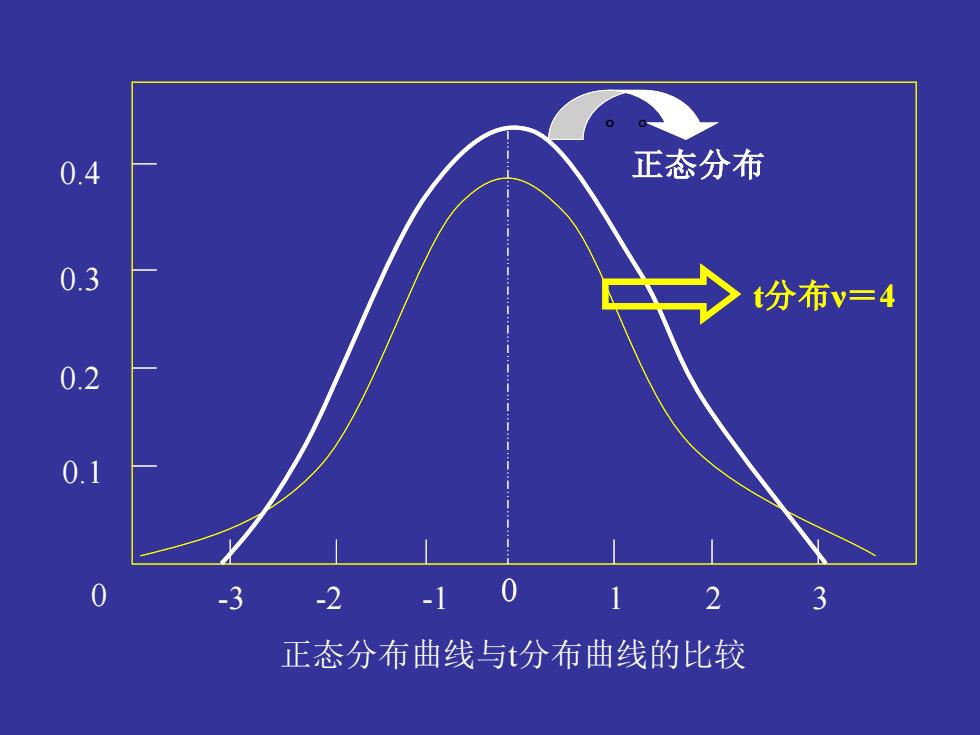
0.4 正态分布 0.3 t分布v=4 0.2 -3 -2-10 2 正态分布曲线与t分布曲线的比较
。 正态分布 t分布ν=4 0 。 正态分布 t分布ν=4 0 0 0.1 0.2 0.3 0.4 -3 -2 -1 1 2 3 正态分布曲线与t分布曲线的比较

2、单个样本平均数的假设测验 例:某春小麦良种的千粒重0=34g,现自外地引入一高产品 种,在8个小区种植,得其千粒重为:35.6、37.6、33.4、35.1、 32.7、36.8、35.9、34.6,问新引入品种的千粒重与当地良种有无 显著差异? 分析:因总体方差未知,又是小样本,故需用t测验。 假设H6:W=u0=34g,HA:U≠34g。 显著水平a=0.05
2、单个样本平均数的假设测验 例:某春小麦良种的千粒重μ0=34g,现自外地引入一高产品 种,在8个小区种植,得其千粒重为:35.6、37.6、33.4、35.1、 32.7、36.8、35.9、34.6,问新引入品种的千粒重与当地良种有无 显著差异? 分析:因总体方差未知,又是小样本,故需用 t 测验。 假设H0: μ= μ0=34g, HA: μ≠ 34g。 显著水平α=0.05

依据:t=氏-四=(-) W0=34g SIn x=(35.6+37.6+.+34.6)/8=35.2(g) SS=∑x2+(∑x)2/8=18.83 SS 18.83 S= Vn-1 =1.64(g) 7 S 1.64 Sx- n 8 =0.58(g) 35.2-34 t= =2.069 0.58
2.069 0.58 35.2 34 0.58( ) 8 1.64 1.64( ) 7 18.83 1 ( ) / 8 18.83 (35.6 37.6 . 34.6)/ 8 35.2( ) 2 2 = − = = = = = = − = = + = = + + + = t g n S S g n SS S SS x x x g x S n x S x t x / ( ) ( − ) = − 依据: = μ0=34g
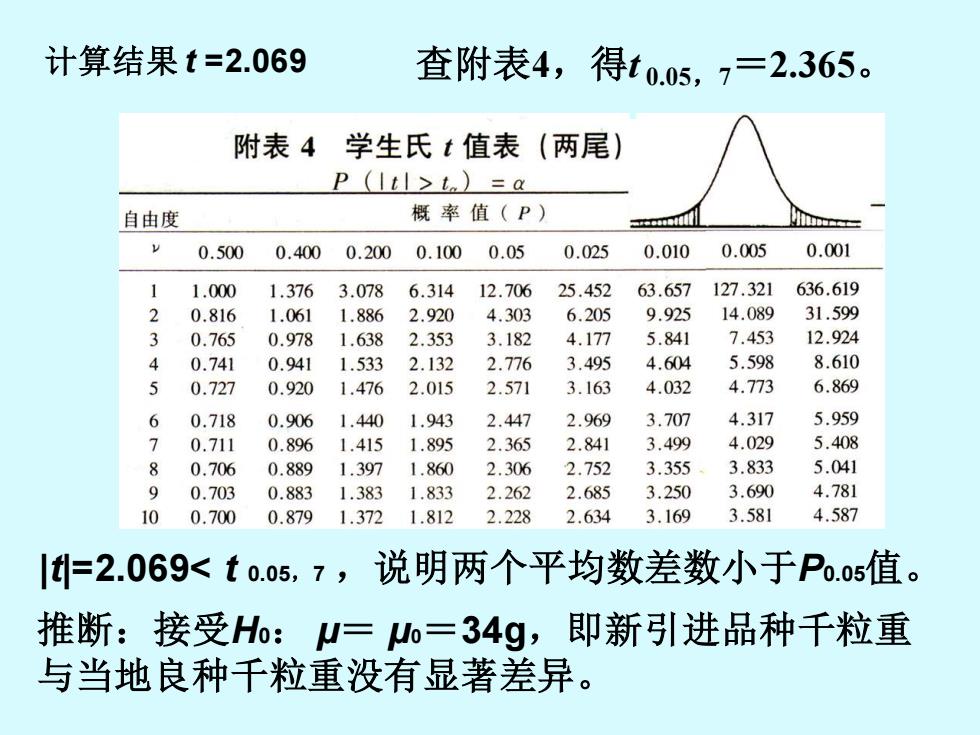
计算结果t=2.069 查附表4,得t0.05,7=2.365。 附表4学生氏t值表(两尾) P (lilzt)=a 自由度 概率值(P) 0.500 0.400 0.200 0.100 0.05 0.025 0.010 0.005 0.001 1.000 1.376 3.078 6.314 12.706 25.452 63.657127.321 636.619 2 0.816 1.061 1.886 2.920 4.303 6.205 9.925 14.089 31.599 3 0.765 0.978 1.6382.353 3.182 4.177 5.841 7.453 12.924 4 0.741 0.9411.533 2.132 2.776 3.495 4.604 5.598 8.610 5 0.727 0.920 1.4762.015 2.571 3.163 4.032 4.773 6.869 6 0.718 0.906 1.4401.943 2.447 2.969 3.707 4.317 5.959 > 0.711 0.8961.415 1.895 2.365 2.841 3.499 4.029 5.408 0.706 0.889 1.3971.860 2.306 2.752 3.355. 3.833 5.041 9 0.703 0.883 1.3831.833 2.262 2.685 3.250 3.690 4.781 10 0.700 0.8791.372 1.812 2.228 2.634 3.169 3.581 4.587 |t=2.069<to.o5,7,说明两个平均数差数小于Po.o5值。 推断:接受Ho:W=Wo=34g,即新引进品种千粒重 与当地良种千粒重没有显著差异
查附表4,得t 0.05,7=2.365。 推断:接受H0: μ= μ0=34g,即新引进品种千粒重 与当地良种千粒重没有显著差异。 |t|=2.069< t 0.05,7 ,说明两个平均数差数小于P0.05值。 计算结果 t =2.069

3、两个样本平均数相比较的假设测]验 (1)成组数据的平均数处比较 如果两个处理完全随机设计,而处理间的 各供试单位彼此独立,则不论两个处理的样本 容量是否相同,所得数据皆为成组数据。成组 数据的平均数的比较又依两个样本所属总体方 差是否已知和样本大小而采用不同的测验方法。 A:O1,o2已知,用U测验。 B:1, 2未知,但可假设δ,=δ2=δ,且两个样本为小样本时,用t测验。 C:01, 02未知, 但不能假设δ1=δ2,用t测验
3、两个样本平均数相比较的假设测验 如果两个处理完全随机设计,而处理间的 各供试单位彼此独立,则不论两个处理的样本 容量是否相同,所得数据皆为成组数据。成组 数据的平均数的比较又依两个样本所属总体方 差是否已知和样本大小而采用不同的测验方法。 (1)成组数据的平均数比较 A:σ1,σ2已知,用U测验。 B: σ1,σ2未知,但可假设δ1=δ2= δ,且两个样本为小样本时,用 t 测验。 C: σ1,σ2未知,但不能假设δ1=δ2,用t 测验

A:δ1,2已知时,用U测验。 2 n U=医-)-(4-4)=天-五 0x-) 0x-
1 2 1 2 1 2 1 2 1 2 ( ) ( ) x x x x x x x x U − − − = − − − = A:δ1, δ2已知时,用U测验。 2 2 2 1 2 1 1 2 n n x x − = +

例1:己知某小麦品种每平方米产量的方差为0.4斤。 今在该品种的一块地上用A、B两法取样,A法取12 个样点,产量为1.2斤/m2;B法取8个样点,产量为 1.4斤/m。试比较两法每平方米的产量是否有显著 差异? 分析:总体方差己知,故采用U测验。 假设:H0:41=2;HA:1≠2 显著水平:0=0.05
例1:已知某小麦品种每平方米产量的方差为0.4斤。 今在该品种的一块地上用A、B两法取样,A法取12 个样点,产量为1.2斤/m2;B法取8个样点,产量为 1.4斤/m2。试比较两法每平方米的产量是否有显著 差异? 分析:总体方差已知,故采用U测验。 假设:H0:μ1= μ2;HA: μ1≠ μ2。 显著水平:α=0.05