
第三章方差分析 Chapter 3 ANOVA (Analysis of Variance)
第三章 方差分析 Chapter 3 ANOVA (Analysis of Variance)

第三章方差分析 方差是平方和除以自由度的商。 02= ∑(xi-4)2 o2=02/n N 方差分析是判断多组数据(3)之间平均数差异是 否显著的一种假设测验方法。2个样本平均数可用t或测验 的方法来评定其差数的显著性。如果有K个平均数,且3, 若仍然用两两比较的方法来测验,则需要作K(K-1)/2次测验, 如果K=10,则需要45次测验,不但测验程序繁琐,而且在 理论上,其显著水平已经扩大了。因此,对于多样本平均数 的假设测验,需采用一种更为合适的统计方法,即方差分析 法(Fisher,1923)
方差分析是判断多组数据(K≥3 )之间平均数差异是 否显著的一种假设测验方法。2个样本平均数可用t 或U测验 的方法来评定其差数的显著性。如果有K个平均数,且K≥3, 若仍然用两两比较的方法来测验,则需要作K(K-1)/2次测验, 如果K=10,则需要45次测验,不但测验程序繁琐,而且在 理论上,其显著水平已经扩大了。因此,对于多样本平均数 的假设测验,需采用一种更为合适的统计方法,即方差分析 法(Fisher, 1923)。 第三章 方差分析 方差是平方和除以自由度的商。 N x i− = 2 2 ( ) n x / 2 2 =

第三章方差分析 例如,若有5组数据要比较,则共需要比较(5×4)/2=10次。 若H0正确,每次接受的概率为1一a=0.95,10次都接受的 概率为0.9510≈0.60,因此,a'=1一0.60=0.40,即犯第一类 错误的概率为0.40,这显然是不能接受的。 方差分析是将总变异分裂为各个因素的相应变异,作 出其数量估计,从而发现各个因素在变异中所占的重要程 度,而且除了可控制因素所引起的变异后,其剩余变异又 可提供试验误差的准确而无偏的估计,作为统计假设测验 的依据
方差分析是将总变异分裂为各个因素的相应变异,作 出其数量估计,从而发现各个因素在变异中所占的重要程 度,而且除了可控制因素所引起的变异后,其剩余变异又 可提供试验误差的准确而无偏的估计,作为统计假设测验 的依据。 第三章 方差分析 例如,若有5组数据要比较,则共需要比较(5×4)/2=10次。 若H0正确,每次接受的概率为1-α=0.95,10次都接受的 概率为0.9510≈0.60,因此,α’=1-0.60=0.40,即犯第一类 错误的概率为0.40,这显然是不能接受的

第三章方差分析 本章主要内容: 第一节方差分析的基本原理和方法。 第二节单向分组资料的方差分析。 第三节两向分组资料的方差分析
本章主要内容: 第一节 方差分析的基本原理和方法。 第二节 单向分组资料的方差分析。 第三节 两向分组资料的方差分析。 第三章 方差分析

第三章方差分析 第一节方差分析的基本原理和方法 1.自由度和平方和的分解 2.F分布(F Distribution) 3.多重比较(multiple comparisons) 4.方差分析的基本假定 5.数据转换
第一节 方差分析的基本原理和方法 1. 自由度和平方和的分解 2. F分布(F Distribution) 3. 多重比较(multiple comparisons) 4. 方差分析的基本假定 5. 数据转换 第三章 方差分析
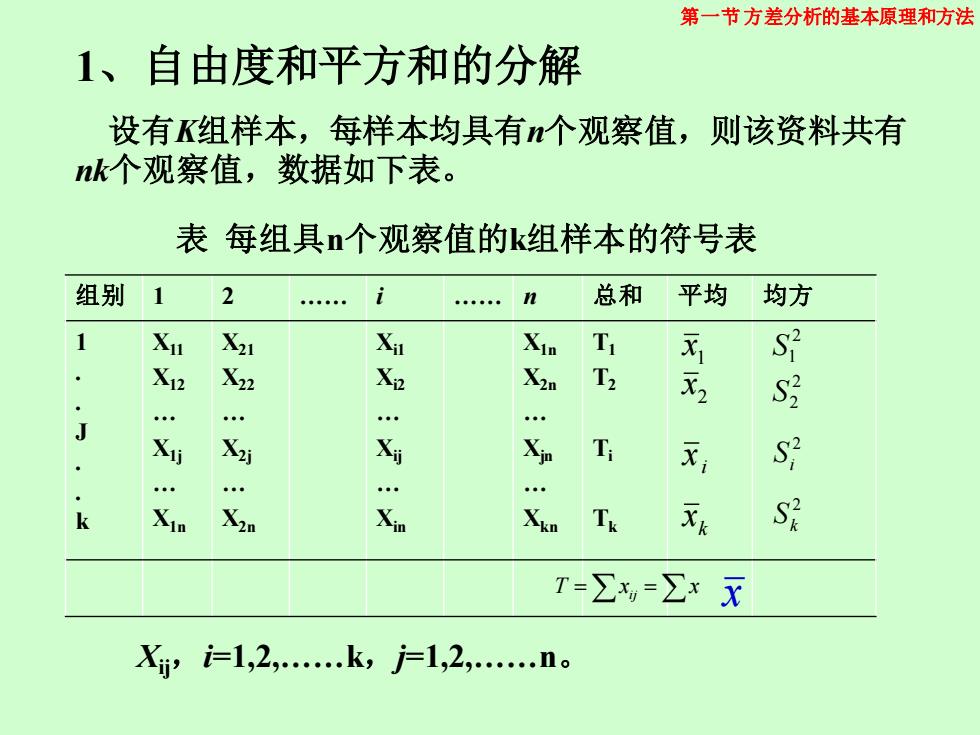
第一节方差分析的基本原理和方法 1、自由度和平方和的分解 设有K组样本,每样本均具有个观察值,则该资料共有 nk个观察值,数据如下表。 表每组具个观察值的k组样本的符号表 组别 . 总和 平均 均方 1 Xu X21 X Xin T 1 S X12 Xi2 X2n T2 X2 S . . J X X Xin T S k Tk Xk S T=∑,=∑xX Xyi=1,2,.k,j-1,2,.n
1、自由度和平方和的分解 设有K组样本,每样本均具有n个观察值,则该资料共有 nk个观察值,数据如下表。 组别 1 2 . i . n 总和 平均 均方 1 . . J . . k X11 X12 . X1j . X1n X21 X22 . X2j . X2n Xi1 Xi2 . Xij . Xin X1n X2n . Xjn . Xkn T1 T2 Ti Tk 表 每组具n个观察值的k组样本的符号表 1 x 2 x i x k x T =x =x ij x 2 1 S 2 2 S 2 i S 2 k S 第一节方差分析的基本原理和方法 Xij,i=1,2,.k,j=1,2,.n

第一节方差分析的基本原理和方法 总平方和(SS 总变异是nk个观察值的变异,故其自由度为 nk一1,平方和SS为: s,-220-Σ nk nk (T-c 式中,C称为矫正数。 nk -Σr-g-∑-c
总变异是nk个观察值的变异,故其自由度为 nk-1,平方和SST为: nk T x nk x SS x x x T 2 2 2 2 2 ( ) ( ) = ( − ) = − = − 式中,C 称为矫正数。 总平方和 (SST ) 第一节方差分析的基本原理和方法 C nk T = 2 ( ) x C nk T SS x T = − = − 2 2 2 ( )

总平方和SS的计算: 气-,-元+年-到 =26-+22X怎-0+2x- =∑(x,-x+民-x 5,=2x,-立2(x,-产+n2,- 总平方和SST=组内平方和SSe十处理平方和SSt
= = − = − + − n j i j i i n j i j x x x x x x 1 2 1 2 ( ) ( ) = = = = − + − − + − n j i n j i j i i n j i j i x x x x x x x x 1 2 1 1 2 ( ) 2( )( ) ( ) 2 1 2 (x x ) n(x x) i n j = ij − i + − = = = = = = = − = − + − k i i k i n j i j i k i n j T i j SS x x x x n x x 1 2 1 1 2 1 1 2 ( ) ( ) ( ) 总平方和SST=组内平方和SSe+处理平方和SSt 总平方和SST的计算:

第一节方差分析的基本原理和方法 上述总变异的自由度和平方和可分解为组间和组内两个 部分。组间变异即k个平均数的变异,故其自由度为k一1, 平方和SSt为: SS,=n∑(c-x)2 组内的变异为各组内观察值与组平均数的相差,故每组 具有一1个自由度,平方和为∑(s,-x)》,而总共有k组资料, 故组内自由度为k(n一1),而组内平方和SSe为: w-空s-
组内的变异为各组内观察值与组平均数的相差,故每组 具有n-1个自由度,平方和为 ,而总共有k 组资料, 故组内自由度为k(n-1),而组内平方和SSe为: 2 ( − ) ij i x x t k i T n j SSe xi j xi = SS − SS = − =1 =1 2 ( ) 第一节方差分析的基本原理和方法 上述总变异的自由度和平方和可分解为组间和组内两个 部分。组间变异即k个平均数的变异,故其自由度为k-1, 平方和 SSt 为: = − 2 SS n (x x) t i

第一节方差分析的基本原理和方法 因此,上述资料的自由度和平方和的分解式为: 总自由度=组间自由度十组内自由度 (nk-1)=(k-1)+k(n-1) 总平方和=组间平方和十组内平方和 ∑馬到=应属-区馬门
因此,上述资料的自由度和平方和的分解式为: 总自由度=组间自由度 + 组内自由度 (nk-1)=(k-1)+ k(n-1) 总平方和=组间平方和 + 组内平方和 = = = − = − + − k i n j i j i k i i n k i j x x n x x x x 1 1 2 1 2 1 2 ( ) ( ) [ ( ) ] 第一节方差分析的基本原理和方法