
第二节统计假设测验 Test of statistical hypothesis 1、统计假设测验的基本步骤 2、两尾测验与一尾测验 3、假设测验的两类错误
第二节 统计假设测验 Test of statistical hypothesis 1、统计假设测验的基本步骤 2、两尾测验与一尾测验 3、假设测验的两类错误

·问题的提出:试验结果能否反映实际情况? 概念: 样本:试验研究的一组数据。 表面效应:观察到的现象(试验结果) 。 统计假设(statistical hypothesis):假设某一试验结果与原 来设想的“不一样”或“一样”,称为统计假设 。 统计假设测验(Test of statistical hypothesis):先设置处理 (Treatment)(水平Level)无效(无效假设),再依据假设 的概率大小来判断接受或否定该假设的过程。 统计推断是:将试验的表面效应与误差大小相比较,由表 面效应可能属于误差的概率作出推断的方法
• 问题的提出:试验结果能否反映实际情况? • 概念: 样本:试验研究的一组数据。 表面效应:观察到的现象(试验结果), • 统计假设(statistical hypothesis):假设某一试验结果与原 来设想的“不一样”或“一样”,称为统计假设。 • 统计假设测验(Test of statistical hypothesis):先设置处理 (Treatment)(水平Level)无效(无效假设),再依据假设 的概率大小来判断接受或否定该假设的过程。 • 统计推断是:将试验的表面效应与误差大小相比较,由表 面效应可能属于误差的概率作出推断的方法

1、统计假设测验的基本步骤 1.1提出无效假设 无效假设(HoNull hypothesis),Ho:W=Wo或 1=2,总体平均数(Wo) 备择假设(H Alternative hypothesis),Ha:W≠ 0或1≠2。 1.2确定显著水平a值(significance level) 确定接受区或否定区的范围。 记做a=0.05或a=0.01
1、统计假设测验的基本步骤 1.1 提出无效假设 无效假设(H0 Null hypothesis),H0:µ=µ0 或 µ1=µ2,总体平均数(µ0) 备择假设(HA Alternative hypothesis),HA:µ ≠ µ0 或µ1 ≠ µ2 。 1.2 确定显著水平α值 (significance level) 确定接受区或否定区的范围。 记做α=0.05 或α=0.01

·显著水平(Significant leve):用来测验假设的概率 标准,常用a来表示,如a=0.01,a=0.05。其取 值的大小由我们的试验材料、试验结果的要求、 我们希望最大可容忍的下错误结论的危险性等所 决定的
• 显著水平(Significant level):用来测验假设的概率 标准,常用α来表示,如α=0.01,α=0.05。其取 值的大小由我们的试验材料、试验结果的要求、 我们希望最大可容忍的下错误结论的危险性等所 决定的
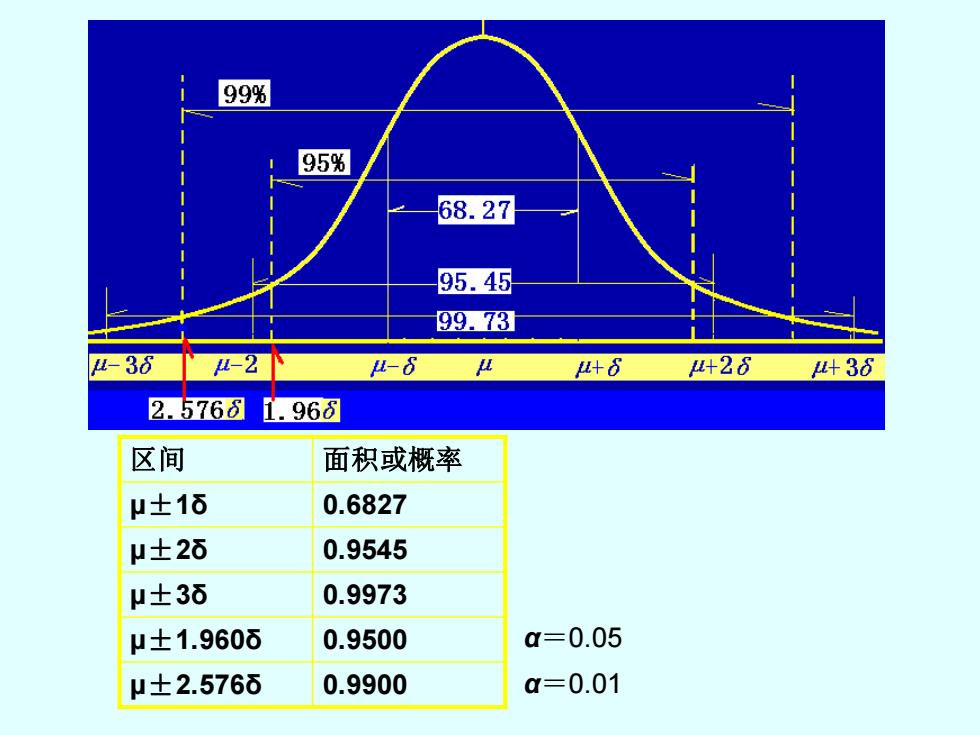
99% 95% 68.27 95.45 99.73 -38 -2N u-68 μ u+6 +28 U+36 2.5768 1.968 区间 面积或概率 μ士1δ 0.6827 μ士2δ 0.9545 μ士3δ 0.9973 μ±1.960δ 0.9500 a=0.05 μ±2.576δ 0.9900 a=0.01
区间 面积或概率 μ±1δ 0.6827 μ±2δ 0.9545 μ±3δ 0.9973 μ±1.960δ 0.9500 μ±2.576δ 0.9900 α=0.05 α=0.01

1.3区间估计(Confidence interval timation) 区间估计是在一定概率保证下,某一参数的取值范围 。1 获得平均数的抽样分布,计算假设正确的概率 ·一个样本与总体的比较用测验。 u=年-H Ox ·查u测验表,要求x≤4+1.96o或x≥4-1.96o 1.4依据“小概率事件实际不可能发生”原理 接受或否定无效假设 1% -<-1.96=
1.3区间估计(Confidence interval timation) • 区间估计是在一定概率保证下,某一参数的取值范围 • 获得平均数的抽样分布,计算假设正确的概率 • 一个样本与总体的比较用 u 测验。 • 查u 测验表,要求 或 x x u − = = − 1.96 x x p = − − 1.96 x x p 1.4 依据“小概率事件实际不可能发生”原理 接受或否定无效假设 x +1.96 x −1.96
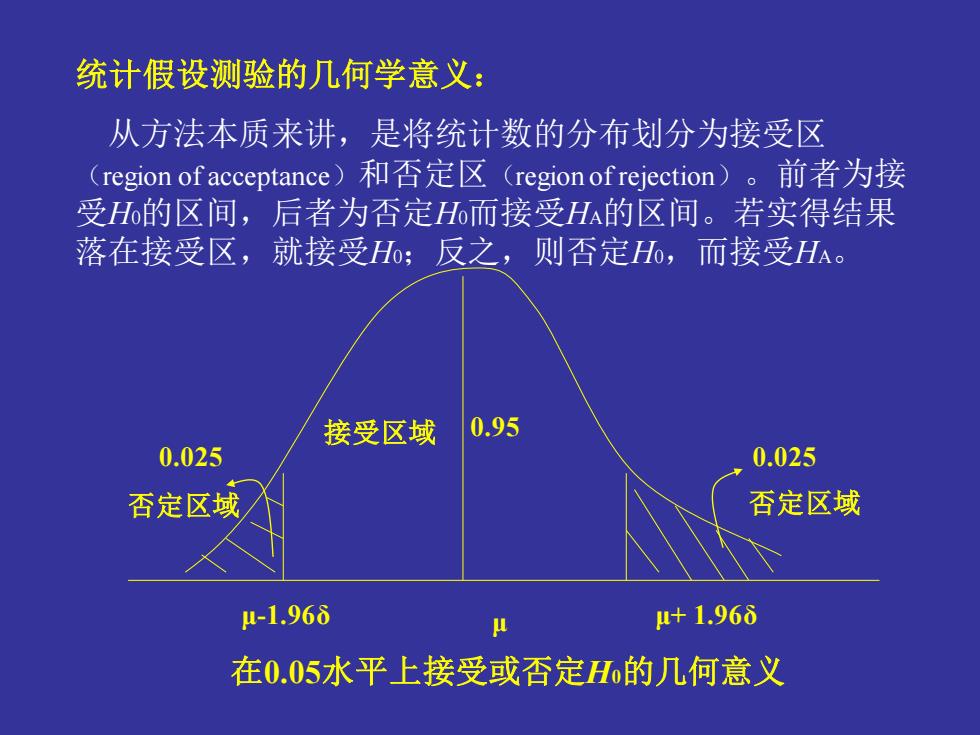
统计假设测验的几何学意义: 从方法本质来讲,是将统计数的分布划分为接受区 (region of acceptance)和否定区(region of rejection)。前者为接 受H的区间,后者为否定H6而接受H的区间。若实得结果 落在接受区,就接受Ho;反之,则否定o,而接受HA。 接受区域 0.95 0.025 0.025 否定区域 否定区域 1-1.966 单 +1.966 在0.05水平上接受或否定H的几何意义
统计假设测验的几何学意义: 从方法本质来讲,是将统计数的分布划分为接受区 (region of acceptance)和否定区(region of rejection)。前者为接 受H0的区间,后者为否定H0而接受HA的区间。若实得结果 落在接受区,就接受H0;反之,则否定H0,而接受HA。 μ-1.96δ μ μ+ 1.96δ 0.95 0.025 0.025 接受区域 否定区域 否定区域 在0.05水平上接受或否定H0的几何意义

例题: 某地小麦品种的一般产量为300kg/667m2, 标准差为75kg。现有一新品种试种后产量为 330kg/6672(样本),试问这个新品种是否较当地 般品种的产量高或不高? 分析:o=300kg,S=75kg,W=330kg。 要求判断W>6或Wo
例题: 某地小麦品种的一般产量为300kg/667m2 , 标准差为75kg。现有一新品种试种后产量为 330kg/667m2 (样本),试问这个新品种是否较当地 一般品种的产量高或不高? 分析:μ0=300kg, S= 75kg,μ=330kg 。 要求判断μ>μ0或μ≯μ0

分析1: ·①、观察从这样一个总体中抽出一个X=330kg的样本所代表 的群体(W与原群体(o)是否一致? 。 ②、设立无效假设=0=300kg。 备择假设≠0。 ③、如果抽取(W1)这种可能性很小,我们只能认为W与W1差别 不大,即W=很可能成立。说明在假设=1成立的条件下, 抽出这样一个样本的事件是一个小概率事件。 ④、小概率事件在一次观察中是不应发生的,但它现在发生 了,一个合理的解释是我们的调查工作有问题,出现这个 现象的原因是取样误差,即应该接受W=0。换句话说,该 新品种的产量与当地原品种没有明显差异
分析1: • ①、观察从这样一个总体中抽出一个 =330kg的样本所代表 的群体(μ)与原群体(μ0)是否一致? • ②、设立无效假设μ=μ0=300kg。 备择假设μ≠ μ0。 ③、如果抽取(μ1)这种可能性很小,我们只能认为μ与μ1差别 不大,即μ=μ1很可能成立。说明在假设μ=μ1成立的条件下, 抽出这样一个样本的事件是一个小概率事件。 ④、小概率事件在一次观察中是不应发生的,但它现在发生 了,一个合理的解释是我们的调查工作有问题,出现这个 现象的原因是取样误差,即应该接受μ=μ0。换句话说, 该 新品种的产量与当地原品种没有明显差异。 x

分析2: 。 ①、观察从这样一个总体中抽出一个元=330kg的样本所代表 的群体(W与原群体(o)是否一致? ·②、设立无效假设=W0=300g。 备择假设≠0。 ③、如果抽取(W)这种可能性很大,我们只能认为与W1差别 不大,即w=不可能成立。说明在假设=1成立的条件下, 抽出这样一个样本的事件是一个小概率事件。 ④、小概率事件在一次观察中是不应发生的,但它现在发生 了,一个合理的解释是我们的调查工作有问题,出现这个 现象的原因是取样误差,即应该接受=0。换句话说,该 新品种的产量确实比当地原品种的产量高
分析2: • ①、观察从这样一个总体中抽出一个 =330kg的样本所代表 的群体(μ)与原群体(μ0)是否一致? • ②、设立无效假设μ=μ0=300kg。 备择假设μ≠ μ0。 ③、如果抽取(μ1)这种可能性很大,我们只能认为μ与μ1差别 不大,即μ=μ1不可能成立。说明在假设μ=μ1成立的条件下, 抽出这样一个样本的事件是一个小概率事件。 ④、小概率事件在一次观察中是不应发生的,但它现在发生 了,一个合理的解释是我们的调查工作有问题,出现这个 现象的原因是取样误差,即应该接受μ=μ0。换句话说, 该 新品种的产量确实比当地原品种的产量高。 x