
第四章统计分布的数值特征 一、判断题 1.全距数值愈小,反映变量值越分散,标志变动度愈小。() 2.众数是总体中出现最多的次数。( 3.平均差与标准差都表示各标志值对算术平均数的平均距离。 4.在钟型分布的情况下,中位数一般介于众数与算术平均数之间。() 5.均值是最常用的集中趋势的测度值之一,它也是一组数据的均衡点所在,因此 它不受极端值的影响。() 6.对同一数列,同时计算平均差和标准差,两者数值必然相等。() 7.均值和调和平均数只是使用了不同的数据,因此调和平均数可以看成是均值的 定类数据可以计算众数,也可以计算中位数。 9.测试集中趋势就是寻找数据的一般水平的代表值或中心值。() 10.不同类型的数据可以用不同类型的集中趋势测度值。() 1山.低层次数据的集中趋势的测度值适用于高层次的测量数据。反过来高层次的 集中趋势的测度 并不适用低层次的测量数据」 1 7差为9,离散系数为30% 则其平均数等于30。 13.调和平均数同均值一样不能用于定类数据和定序数据,可以用于定量数据。 14.定序数据可以计算众数、中位数和分位数。() 15.中位数和众数都不受极端值的影响。 16.交替标志的乎 均数等于P。 17.当均值<中位数<众数时,总体呈左偏分布。() 18.当均值=中位数=众数时,总体呈正态分布。() 19.均值主要用于数值型数据。() 二、单项选择题 1.总量指标按其反映时间状况不同,可以分为() A.总体总量和标志总量 B.总体总量和时期指标 C.标志总量和时期指标 D.时点指标和时期指标。 2.总量指标按其反映内容的不同,可以分为() A村占指标和村期指标 B村期指标和标志总量 C总体单位总量和总体标志总量 D.总体总量和时点指标 3.2002年某地区下岗职工已安置了13.7万人,安置率达80.6%,安置率是() A.总量指标 B.相对指标 C.平均指标D.变异指标 4.产品合格率,设备利用率这两个相对数是() A.结构相对数B.强度相对数C.比例相对数 D.出较相对数 5.我国第四次人口普查结果,我国男女之间的对比关系为1.063:1,这个指标是 A.比较相对数B.比例相对数C.强度相对数D.结构相对数 6.加权算术平均数x的大小() A.受各组次数f的影响最大 B.受各组标志值x的影响最大
1 第四章 统计分布的数值特征 一、判断题 1.全距数值愈小,反映变量值越分散,标志变动度愈小。( ) 2.众数是总体中出现最多的次数。( ) 3.平均差与标准差都表示各标志值对算术平均数的平均距离。( ) 4.在钟型分布的情况下,中位数一般介于众数与算术平均数之间。( ) 5.均值是最常用的集中趋势的测度值之一,它也是一组数据的均衡点所在,因此 它不受极端值的影响。( ) 6.对同一数列,同时计算平均差和标准差,两者数值必然相等。( ) 7.均值和调和平均数只是使用了不同的数据,因此调和平均数可以看成是均值的 变形( ) 8.定类数据可以计算众数,也可以计算中位数。( ) 9.测试集中趋势就是寻找数据的一般水平的代表值或中心值。( ) 10.不同类型的数据可以用不同类型的集中趋势测度值。( ) 11.低层次数据的集中趋势的测度值适用于高层次的测量数据。反过来高层次的 集中趋势的测度值,并不适用低层次的测量数据。( ) 12. 已知一组数列的方差为 9,离散系数为 30%,则其平均数等于 30。( ) 13. 调和平均数同均值一样不能用于定类数据和定序数据,可以用于定量数据。 ( ) 14.定序数据可以计算众数、中位数和分位数。( ) 15.中位数和众数都不受极端值的影响。( ) 16.交替标志的平均数等于 P。( ) 17.当均值<中位数<众数时,总体呈左偏分布。( ) 18.当均值=中位数=众数时,总体呈正态分布。( ) 19.均值主要用于数值型数据。( ) 二、单项选择题 1.总量指标按其反映时间状况不同,可以分为( ) A.总体总量和标志总量 B.总体总量和时期指标 C.标志总量和时期指标 D.时点指标和时期指标。 2.总量指标按其反映内容的不同,可以分为( ) A.时点指标和时期指标 B.时期指标和标志总量 C.总体单位总量和总体标志总量 D.总体总量和时点指标。 3.2002 年某地区下岗职工已安置了 13.7 万人,安置率达 80.6%,安置率是( ) A.总量指标 B.相对指标 C.平均指标 D.变异指标 4.产品合格率,设备利用率这两个相对数是( ) A.结构相对数 B.强度相对数 C.比例相对数 D.比较相对数 5.我国第四次人口普查结果,我国男女之间的对比关系为 1.063:1,这个指标是 ( ) A.比较相对数 B.比例相对数 C.强度相对数 D.结构相对数 6.加权算术平均数 x 的大小( ) A.受各组次数 f 的影响最大 B.受各组标志值 x 的影响最大

C.只受各组标志值x的影响D.受各组标志值x和次数f的共同影响 7.权数对算术平均数的影响作用,决定于() A.权数本身数值的大小 B.作为权数的单位数占总体单位数的比重大小 C.各组标志的大小 D.权数的经济意义 8.分配数列中,当标志值较小,而权数较大时,计算出来的算术平均数() A.接近于标志值大的一方 B.接近于标志值小的一方 C.接近于大小合适的标志值 D不受权粉影向 9.平均指标反映 A.总体分布的集中趋势 B.总体分布的特征 C.总体单位的集中趋势 D.总体变动趋势。 10.某公司下属5个企业,共有2000名工人。已知每个企业某月产值计划完成百 分比和实际产值,要计算该公司月平均产值计划完成程度,应采用加权调和平均 数的方法计算,其权数是( 1.计划产值 B.实际产值 C.工人数 D.企业数 11.某副食品公司所属3个商店1990年计划规定销售额分别为500万元、600万 元、800万元,其执行结果分别完成计划104%、105%、105%,则该公司所属的3 个商店平均完成计划的百分数是() A.101%1+105%x2-=10467% B.104%×500+105%x60+105%×80-104.74% 00+600+8 C.- 500+600+800 D.31049%×105%×105%=10467% 500 600 800 1049%+105%+1059% 12.标志变异指标中易受极端数值影响的是() A.全距 B平均差 C标准差 D.标准差系数 13.用是非标志计算平均数,其计算结果为() A.D十 B.p-a ,1一D D.D 14.某单位职工的平均年龄为32岁,这是对()的平均。 A变最 B.变量值 C.数量标志 D.数量指标 15.平均差的主要缺占是() A.与标准差相比计算复杂 B.易受极端数值的影响 C.不符合代数演算方法 D.计算结果比标准差数值大 16.两个总体的平均数不等,但标准差相等,则( A.平均数小,代表性大 B.平均数大,代表性大 C.两个平均数代表性相同D.无法进行正确判断 17.在变量数列中,计算标准差的公式为( ∑x-xf ∑x-xf n B.Σf ∑-x/ - C.∑f D. 18.标准差数值越小,则反映变量值() A.越分散,平均数代表性越低 B越集中,平均数代表性越高
2 C.只受各组标志值 x 的影响 D.受各组标志值 x 和次数 f 的共同影响 7.权数对算术平均数的影响作用,决定于( ) A.权数本身数值的大小 B.作为权数的单位数占总体单位数的比重大小 C.各组标志的大小 D.权数的经济意义 8.分配数列中,当标志值较小,而权数较大时,计算出来的算术平均数( ) A.接近于标志值大的一方 B.接近于标志值小的一方 C.接近于大小合适的标志值 D.不受权数影响 9.平均指标反映了( ) A.总体分布的集中趋势 B.总体分布的特征 C.总体单位的集中趋势 D.总体变动趋势。 10.某公司下属 5 个企业,共有 2000 名工人。已知每个企业某月产值计划完成百 分比和实际产值,要计算该公司月平均产值计划完成程度,应采用加权调和平均 数的方法计算,其权数是( ) A.计划产值 B.实际产值 C.工人数 D.企业数 11.某副食品公司所属 3 个商店 1990 年计划规定销售额分别为 500 万元、600 万 元、800 万元,其执行结果分别完成计划 104%、105%、105%,则该公司所属的 3 个商店平均完成计划的百分数是( ) A. 104.67% 3 101% 1 105% 2 = + B. 104.74% 500 600 800 104% 500 105% 600 105% 800 = + + + + ; C. 105% 800 105% 600 104% 500 500 600 800 + + + + D. 3 104%105%105% =104.67%。 12.标志变异指标中易受极端数值影响的是( ) A.全距 B.平均差 C.标准差 D.标准差系数 13.用是非标志计算平均数,其计算结果为( ) A. p+q B. p-q C. 1-p D. p 14.某单位职工的平均年龄为 32 岁,这是对( )的平均。 A.变量 B. 变量值 C.数量标志 D. 数量指标 15. 平均差的主要缺点是( ) A.与标准差相比计算复杂 B.易受极端数值的影响 C.不符合代数演算方法 D.计算结果比标准差数值大 16.两个总体的平均数不等,但标准差相等,则( ) A.平均数小,代表性大 B.平均数大,代表性大 C.两个平均数代表性相同 D.无法进行正确判断 17.在变量数列中,计算标准差的公式为( ) A. ( ) n x−x f 2 B. ( ) − f x x f 2 ; C. ( ) − f x x f D. ( ) n x − x 。 18.标准差数值越小,则反映变量值( ) A.越分散,平均数代表性越低 B.越集中,平均数代表性越高

C.越分散,平均数代表性越高 D.越集中,平均数代表性越低 19.标准差属千() A强度相对指标 B.绝对指标 C相村指标 D平的指标 20,若把全部产品分为合格品与不合格品,所采用的标志属于 A.不变标志 B.是非标志 C.品质标志 D.数量标志 21,在甲乙两个变量数列中,若甲<σ乙,则两个变量数列平均数的代表性程度 相比较() A.两个数列的平均数代表性相同 B.甲数列的平均数代表性高于乙数列: C.乙数列的平均数代表性高于甲数列: D.不能确定哪个数列的平均数代表性好一些。 22.总量指标又称为() A.相对数指标 B.平均数指标 C.绝对数指标 D.中位数指标 23.总量指标是认识现象总体数量特征的( A.派生指标 B.基础指标 C.分析指标 D.平均指标 24.下列各项中属于总量指标的是() A.工资总额 B.平均工资 C.人口密度 D.性别比例 25.每百户居民拥有由任机数最是() A总量指标 平均指标 C.强度相对指标 D.比例相对指标 26.动态相对指标计算公式中的分子所代表的时期称为() A.基期 B.报告期 C.标准时间 D.计划期 27.中位数的标志值是总体中( A.出现次数最多的 B.外干列中点位智的 C.调和平均数 D.任一位置的 三、多项选择题 1.总量指标的计量单位有() A.实物单位 B.劳动时间单位 C.价值单位 D百分比知千分出 E.倍数、系数和成数 2.在社会经济中计算总量指标有着重要意义,是因为总量指标是( A.对社会经济现象认识的起点 B.实行社会管理的依据之 C.计算相对指标和平均指标的基础 D.唯一能进行统计推算的指标 E.没有统计误差的统计指标 3.在相对指标中,分子和分母可以互相对换的有0 A.比较相对指 B.比例相对指标 C.动态相对指标 D.结构相对指标 E.强度相对指标 4.下列指标中属于强度相对指标的有( A.按人口计算平均每人占有国民收入 B.人口自然增长率 C.人口密度 D.按人口计算平均每人占有粮食产最 E.人口性别出 5.时点指标的特点是) 实 B.数值只能间断计算 C.数值可以连续相加 D.数值不能直接相加 E.数值大小与所属时间长短无关。 6.标准差和平均差的共同点是0。 3
3 C.越分散,平均数代表性越高 D.越集中,平均数代表性越低 19.标准差属于( ) A.强度相对指标 B.绝对指标 C.相对指标 D.平均指标 20.若把全部产品分为合格品与不合格品,所采用的标志属于( ) A.不变标志 B.是非标志 C.品质标志 D.数量标志 21.在甲乙两个变量数列中,若 甲 ﹤ 乙 ,则两个变量数列平均数的代表性程度 相比较( ) A.两个数列的平均数代表性相同; B.甲数列的平均数代表性高于乙数列; C.乙数列的平均数代表性高于甲数列; D.不能确定哪个数列的平均数代表性好一些。 22. 总量指标又称为( ) A.相对数指标 B.平均数指标 C.绝对数指标 D. 中位数指标 23. 总量指标是认识现象总体数量特征的( ) A.派生指标 B.基础指标 C. 分析指标 D. 平均指标 24. 下列各项中属于总量指标的是( ) A.工资总额 B.平均工资 C.人口密度 D.性别比例 25.每百户居民拥有电话机数量是( ) A 总量指标 B.平均指标 C.强度相对指标 D. 比例相对指标 26.动态相对指标计算公式中的分子所代表的时期称为( ) A.基期 B.报告期 C.标准时间 D.计划期 27.中位数的标志值是总体中( ) A.出现次数最多的 B.处于数列中点位置的 C.调和平均数 D.任一位置的 三、多项选择题 1.总量指标的计量单位有( ) A.实物单位 B.劳动时间单位 C.价值单位 D.百分比和千分比 E.倍数、系数和成数 2.在社会经济中计算总量指标有着重要意义,是因为总量指标是( ) A.对社会经济现象认识的起点 B.实行社会管理的依据之一 C.计算相对指标和平均指标的基础 D.唯一能进行统计推算的指标 E.没有统计误差的统计指标 3.在相对指标中,分子和分母可以互相对换的有() A.比较相对指标 B.比例相对指标 C.动态相对指标; D.结构相对指标 E.强度相对指标 4.下列指标中属于强度相对指标的有( ) A.按人口计算平均每人占有国民收入 B.人口自然增长率 C.人口密度 D.按人口计算平均每人占有粮食产量 E.人口性别比 5.时点指标的特点是( ) A.数值可以连续计算 B.数值只能间断计算 C.数值可以连续相加 D.数值不能直接相加 E.数值大小与所属时间长短无关。 6. 标准差和平均差的共同点是()

A.两者都以平均数为中心来测定总体各单位标志值的离散程度 B.两者在反映总体标志变异程度方面都比全距准确 C.两者都考虑了总体的所有变量值的差异程度 D.两者都受极端值较大影响 E.两者都计算方便 7.加权算术平均数等于简单算术平均数是在() A.各组变量值不相同的条件下B.各组次数相等的条件下 C名细权数都为1的条件下 D.在分细细数较少的条件下 E,各组次数不相签的条件下 8.下列各项中 可以应用加权算术平均法计算平均数的有 A.由各个工人的工资额计算平均工资 B.由工人按工资分组的变量数列计算平均工资 C.由工人总数和工资总额求平均工资 D.由各个环比发展速度求平均发展速度 E.由各产品等级及各级产品产量求平均等级 9.下面关于权数的描述,正确的是0 A.权数是衡量相应的变量对总平均数作用的强度: B.权数起作用在于次数占总次数的比重大小: C.权数起作用在干次数本身绝对值大小: D.权数起作用的前提之一是各组的变量值必须互有差异 王.权数起作用的前提之 是各组的频率必须有差别。 10.某城市表明经济状况的结构相对指标 A.非公经济占49% B.第二产业产值占61% C.人均GNP45000元 D.人均居住面积15f E.在居民中人均月收入1500元以上的有32% 1山.标志变异指标可以反映( A.平均数代表性大小 B.总体单位标志值分布的集中趋势 C.总体单位标志值的离中趋势 D.社会生产过程的均衡性 E.产品质量的稳定性 12.在如下的指标中,平均指标是 A.人均占有国内生产总值 B.人均占有绿化面积 C.平均工资 D.单位产品原材料耗用量 E.居民平均每人生活费支出 13.是非标志的标准差是() A.q+p B.√p C.√p-g D.1-9X1-p) E.p(1-9) 14.众数是() A.处于数列中点位置的标志值 B.总体中出现次数最多的标志信 C.用从表示 D.用M表示 E.不受分配数列中极端值的影向 15.在下列项目中属于时点指标的有() A.全国人口12.5亿人 B.我田粮食4.9亿吨 C年末“网民”1000万 D.全国耕地19.51亿亩 E.1999年邮政亏损144 元 16.两组工人加工同样的零件,第一组工人每人加工零件数为:32、25、29、28 26:第二组工人每人加工零件数为:30、25、22、26、27。这二组工人加工零 件数的变异程度(
4 A.两者都以平均数为中心来测定总体各单位标志值的离散程度 B.两者在反映总体标志变异程度方面都比全距准确 C.两者都考虑了总体的所有变量值的差异程度 D.两者都受极端值较大影响 E.两者都计算方便 7.加权算术平均数等于简单算术平均数是在( ) A.各组变量值不相同的条件下 B.各组次数相等的条件下 C.各组权数都为 1 的条件下 D.在分组组数较少的条件下 E.各组次数不相等的条件下 8.下列各项中,可以应用加权算术平均法计算平均数的有() A.由各个工人的工资额计算平均工资 B.由工人按工资分组的变量数列计算平均工资 C.由工人总数和工资总额求平均工资 D.由各个环比发展速度求平均发展速度 E.由各产品等级及各级产品产量求平均等级 9.下面关于权数的描述,正确的是() A.权数是衡量相应的变量对总平均数作用的强度; B.权数起作用在于次数占总次数的比重大小; C.权数起作用在于次数本身绝对值大小; D.权数起作用的前提之一是各组的变量值必须互有差异; E.权数起作用的前提之一是各组的频率必须有差别。 10.某城市表明经济状况的结构相对指标( ) A.非公经济占 49% B.第二产业产值占 61% C.人均 GNP45000 元 D.人均居住面积 15M2 E.在居民中人均月收入 1500 元以上的有 32% 11.标志变异指标可以反映( ) A.平均数代表性大小 B.总体单位标志值分布的集中趋势 C.总体单位标志值的离中趋势 D.社会生产过程的均衡性 E.产品质量的稳定性 12.在如下的指标中,平均指标是( ) A.人均占有国内生产总值 B.人均占有绿化面积 C.平均工资 D.单位产品原材料耗用量 E.居民平均每人生活费支出 13.是非标志的标准差是( ) A. q + p B. pq C. p − q D. (1− q)(1− p) E. p(1− q) 14.众数是( ) A.处于数列中点位置的标志值 B.总体中出现次数最多的标志值 C.用 MO 表示 D.用 Me 表示 E.不受分配数列中极端值的影响 15.在下列项目中属于时点指标的有( ) A.全国人口 12.5 亿人 B.我国粮食 4.9 亿吨 C.年末“网民”1000 万人 D.全国耕地 19.51 亿亩 E.1999 年邮政亏损 144 亿元 16.两组工人加工同样的零件,第一组工人每人加工零件数为:32、25、29、28、 26;第二组工人每人加工零件数为:30、25、22、26、27。这二组工人加工零 件数的变异程度( )

A.第一组变异程度大于第二组 B.第二组变异程度大于第一组 C.只有A正确 D.只有B正确 E.无法比较。 17.时点指标的数值是( 不能加 B可以加总 C.大小和时点间隔长短有关 D.连续登记的 E.大小和时点间隔长短无关 四、填空题 1.综合指标按其反映现象总体数量特征不同分为总量指标 总量指标是反映社会经济现象总体规模或水平的指标,它是计 和 的堡础。 2.相对指标和平均指标一般都是由两个有关系的 _计算出来的。它 们是总量指标的 指标 3.根据研究目的和比较标准的不同,相对指标可分为 4.不同时点的时点指标不具有 ,数值大小与其 长短无关 5.统计中的变量数列是以 为中心面左右波动,所以平均数反映了 总体分布的」 而标志变异指标则说明变量的 6.权数对算术平均数的影响作用,不决定于权数 的大小,而决 的比面大小 7.相对指标有 和 两种表现形式 8.标志变异指标的大小与平均数代表性的大小成 关系。 9.是非标志的平均数为 ,标准差为 10.某企业职工按工资额分组,最高组为140~150元,最低组为50~60元,其 全距为 五、名词解释 3.平均指标 4.标志变异指标 5.成数 六、简答题 1.什么叫总量指标?计算总量指标有什么作用?总量指标的种类如何分法? 2.什么是相对指标?相对指标的种类、作用有哪些? 3.加权算术平均数和加权调和平均数在计算上有什么不同? 4.简述平均指标的 种 平均指标的计算原则是什么?有何作用? 5.简述标志变异指标的作用。 6.用全距测定标志变异度有哪些优缺点? 7.什么是标志变动度?测定它的方法有几种? 8.简述时点指标和时期指标的特点
5 A.第一组变异程度大于第二组 B.第二组变异程度大于第一组 C.只有 A 正确 D.只有 B 正确 E.无法比较。 17.时点指标的数值是( ) A.不能加总 B.可以加总 C. 大小和时点间隔长短有关 D.连续登记的 E.大小和时点间隔长短无关 四、填空题 1.综合指标按其反映现象总体数量特征不同分为总量指标、_、_。 总量指标是反映社会经济现象总体规模或水平的指标,它是计算 和 的基础。 2.相对指标和平均指标一般都是由两个有关系的 计算出来的。它 们是总量指标的 指标。 3.根据研究目的和比较标准的不同,相对指标可分为 、 、 、 、 和 等六种。 4. 不同时点的时点指标不具有_,数值大小与其_长短无关。 5.统计中的变量数列是以 为中心面左右波动,所以平均数反映了 总体分布的 。而标志变异指标则说明变量的 。 6.权数对算术平均数的影响作用,不决定于权数 的大小,而决 定于权数 的比重大小。 7.相对指标有_和_两种表现形式。 8.标志变异指标的大小与平均数代表性的大小成 关系。 9.是非标志的平均数为 ,标准差为 。 10.某企业职工按工资额分组,最高组为 140~150 元,最低组为 50~60 元,其 全距为 。 五、名词解释 1.总量指标 2.相对指标 3.平均指标 4.标志变异指标 5.成数 六、简答题 1.什么叫总量指标?计算总量指标有什么作用?总量指标的种类如何分法? 2.什么是相对指标?相对指标的种类、作用有哪些? 3.加权算术平均数和加权调和平均数在计算上有什么不同? 4.简述平均指标的种类。平均指标的计算原则是什么?有何作用? 5.简述标志变异指标的作用。 6.用全距测定标志变异度有哪些优缺点? 7.什么是标志变动度?测定它的方法有几种? 8. 简述时点指标和时期指标的特点

七、计算题 1.某百货公司6月份日销售额数据(单位:万元)如下: 销售额数据 257276297252238310240236265278 271 292261281301274267 280291258 272284268303273263322249269295 要求:(1)计算该百货公司日销售额的均值、中位数和四分位数: (2)计算日销售额的标准差。 2.对某地区120家企业按利润额进行分组,结果如下: 表2 利润额分组数据 按利润额分组/万元 企业数/个 200-~300 19 300~400 30 400-500 42 500~600 18 600以上 11 合i计 120 要求:计算120家企业利润额的众数、中位数和均值 一项关于大学生体重状况的研究发现,男生的平均体重为60水g,标准差为 5kg:女生的平均体重为50kg,标准差为5kg。请回答下面的问题: 要求:(1)男生的体重差异大还是女生的体重差异大?为什么?(2)以磅为单 位(1磅=2.2kg)求体重的平均数和标准差。(3)粗略地估计一下,男生中有百 分之几的人体重在55kg 65kg之间? (4)粗略地估计 下,女生中有百分之几 的人体重在40kg~60kg之间。 4.数百万计的美国人每天早上起来会在自己家的办公室里进行工作。个人电脑的 广泛应用是使戴来戴多的人能铭在家里工作的原因之一·。下面是一个样本,它显 示的是在家工作的人的年龄的数据。 表3 年龄数据 22582450295257313041 44404629313732444929 要求:(1)计算平均数和众数。 (2)对于所有成人的总体 其年龄的中位数为35.1岁(美国统计局,199 年11月)。用上面的数据来说明这些在家工作的人的年龄与所有成人的总体相 比是大是小? (3)计算第1和第30分位数 (4)计算第32 百分位数 5.夏威夷旅游局搜集了来当地观光的旅游者的数据。下面的数据来自1994年11
6 七、计算题 1.某百货公司 6 月份日销售额数据(单位:万元)如下: 表 1 销售额数据 257 276 297 252 238 310 240 236 265 278 271 292 261 281 301 274 267 280 291 258 272 284 268 303 273 263 322 249 269 295 要求:(1)计算该百货公司日销售额的均值、中位数和四分位数; (2)计算日销售额的标准差。 2.对某地区 120 家企业按利润额进行分组,结果如下: 表 2 利润额分组数据 按利润额分组/万元 企业数/个 200~300 19 300~400 30 400~500 42 500~600 18 600 以上 11 合计 120 要求:计算 120 家企业利润额的众数、中位数和均值。 3. 一项关于大学生体重状况的研究发现,男生的平均体重为 60kg,标准差为 5kg;女生的平均体重为 50kg,标准差为 5kg。请回答下面的问题: 要求:(1)男生的体重差异大还是女生的体重差异大?为什么?(2)以磅为单 位(1 磅=2.2kg)求体重的平均数和标准差。(3)粗略地估计一下,男生中有百 分之几的人体重在 55kg~65kg 之间?(4)粗略地估计一下,女生中有百分之几 的人体重在 40kg~60kg 之间。 4.数百万计的美国人每天早上起来会在自己家的办公室里进行工作。个人电脑的 广泛应用是使越来越多的人能够在家里工作的原因之一。下面是一个样本,它显 示的是在家工作的人的年龄的数据。 表 3 年龄数据 22 58 24 50 29 52 57 31 30 41 44 40 46 29 31 37 32 44 49 29 要求:(1)计算平均数和众数。 (2)对于所有成人的总体,其年龄的中位数为 35.1 岁(美国统计局,1997 年 11 月)。用上面的数据来说明这些在家工作的人的年龄与所有成人的总体相 比是大是小? (3)计算第 1 和第 3 四分位数。 (4)计算第 32 百分位数。 [ 5.夏威夷旅游局搜集了来当地观光的旅游者的数据。下面的数据来自 1994 年 11
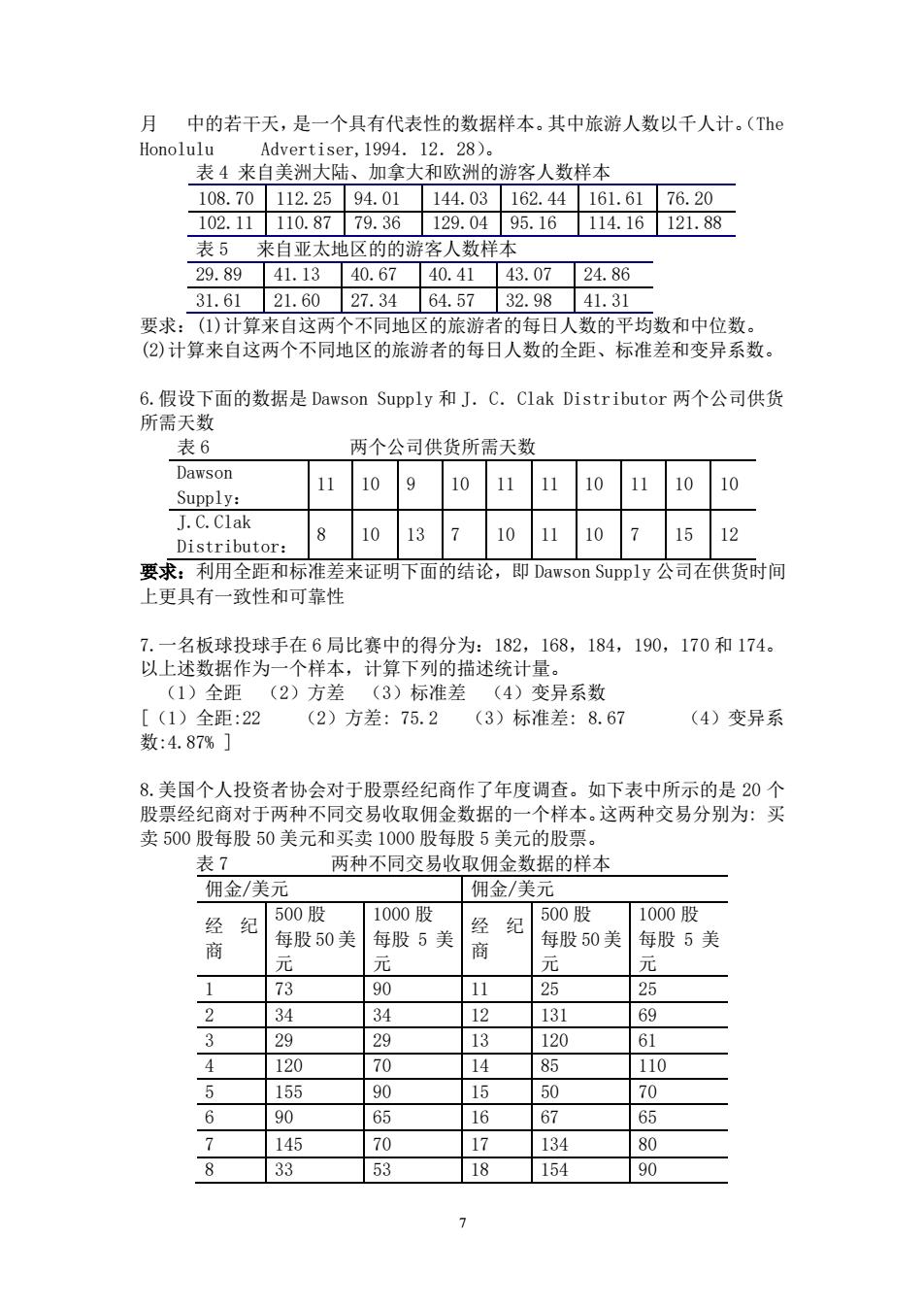
月中的若干天,是一个具有代表性的数据样本。其中旅游人数以千人计。(Te Honolulu Advertiser.1994 12.28) 表4来自美洲大陆、加拿大和欧洲的游客人数样本 108.70112.2594.01144.03162.44161.6176.20 102.11110.8779.36129.0495.16114.16121.88 表5来白亚太地风的的游客人粉样本 29.8941.1340.6740.4143.0724.86 31.6121.6027.3464.5732.9841.31 要求:()计算来自这两个不同地区的旅游者的每日人数的平均数和中位数。 (②)计算来自这两个不同地区的旅游者的每日人数的全距、标准差和变异系数 6.假设下面的数据是Dawson Supply和J.C.Clak Distributor两个公司供货 所需天数 6 两个公司供货所需天数 Dawson 11 10 910 1010 Supply: I C.Clak Distributor: 8 1013710111071512 要求:利用全距和标准差来证明下面的结论,即Dawson Supply公司在供货时间 上更具有一致性和可靠性 7.一名板球投球手在6局比赛中的得分为:182,168,184,190,170和174。 以上述数据作为一个样本,计算下列的描述统计量。 (1)全距(2)方差 (3)标准差(4)变异系数 [(1)全距:22 (2)方差:75.2 (3)标准差:8.67 (4)变异系 数:4.87%] 8.美国个人投资者协会对于股票经纪商作了年度调查。如下表中所示的是20个 股严经纪商对于两种不同交易收取用金数据的一个样本。这两种交易分别为:买 卖500股每股50美元和买卖1000股每股5美元的股票 7 两种不同交易收取佣金数据的样本 佣金/美元 佣金/美元 经纪 500股 1000股 500股 1000股 商 每股50美 每股5美 经纪 每股50美 每股5美 73 90 11 25 25 24 34 12 131 69 29 13 120 61 120 70 14 85 110 155 90 15 50 70 65 16 67 65 145 70 17 134 80 33 53 18 154 90 7
7 月 中的若干天,是一个具有代表性的数据样本。其中旅游人数以千人计。(The Honolulu Advertiser,1994.12.28)。 表 4 来自美洲大陆、加拿大和欧洲的游客人数样本 108.70 112.25 94.01 144.03 162.44 161.61 76.20 102.11 110.87 79.36 129.04 95.16 114.16 121.88 表 5 来自亚太地区的的游客人数样本 29.89 41.13 40.67 40.41 43.07 24.86 31.61 21.60 27.34 64.57 32.98 41.31 要求:(1)计算来自这两个不同地区的旅游者的每日人数的平均数和中位数。 (2)计算来自这两个不同地区的旅游者的每日人数的全距、标准差和变异系数。 6.假设下面的数据是 Dawson Supply 和 J.C.Clak Distributor 两个公司供货 所需天数 表 6 两个公司供货所需天数 Dawson Supply: 11 10 9 10 11 11 10 11 10 10 J.C.Clak Distributor: 8 10 13 7 10 11 10 7 15 12 要求:利用全距和标准差来证明下面的结论,即 Dawson Supply 公司在供货时间 上更具有一致性和可靠性 7.一名板球投球手在 6 局比赛中的得分为:182,168,184,190,170 和 174。 以上述数据作为一个样本,计算下列的描述统计量。 (1)全距 (2)方差 (3)标准差 (4)变异系数 [(1)全距:22 (2)方差: 75.2 (3)标准差: 8.67 (4)变异系 数:4.87% ] 8.美国个人投资者协会对于股票经纪商作了年度调查。如下表中所示的是 20 个 股票经纪商对于两种不同交易收取佣金数据的一个样本。这两种交易分别为: 买 卖 500 股每股 50 美元和买卖 1000 股每股 5 美元的股票。 表 7 两种不同交易收取佣金数据的样本 佣金/美元 佣金/美元 经 纪 商 500 股 每股 50 美 元 1000 股 每股 5 美 元 经 纪 商 500 股 每股 50 美 元 1000 股 每股 5 美 元 1 73 90 11 25 25 2 34 34 12 131 69 3 29 29 13 120 61 4 120 70 14 85 110 5 155 90 15 50 70 6 90 65 16 67 65 7 145 70 17 134 80 8 33 53 18 154 90
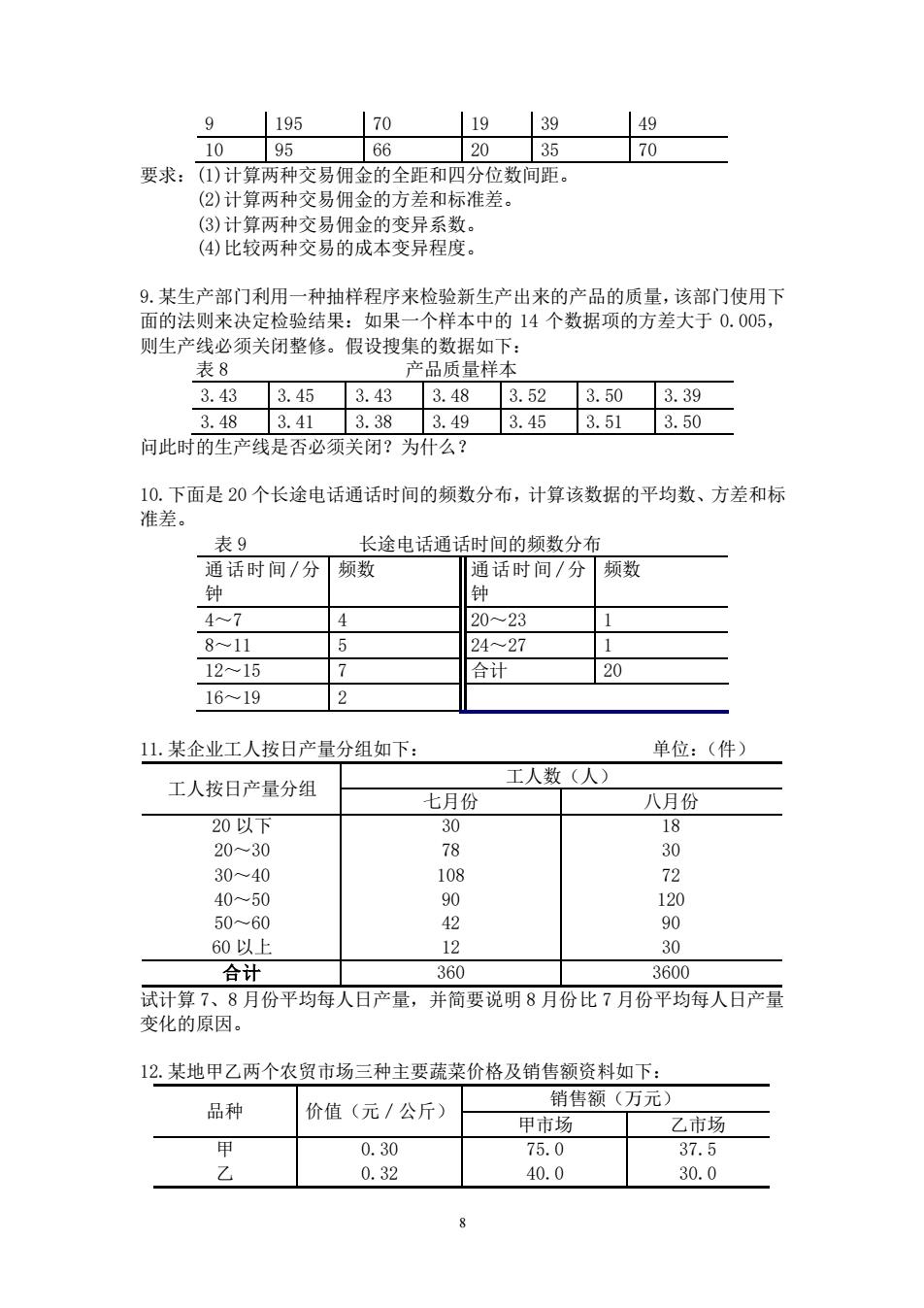
9 |195 170 119|39 49 10 05 66 12035 70 要求:()计算两种交易佣金的全距和四分位数间距。 (2)计算两种交易佣金的方弟和标准差 (3)计算两种交易佣金的变异系数 (4)出较两种衣易的成太变异程府 9.某生产部门利用一种抽样程序来检验新生产出来的产品的质量,该部门使用下 面的法则来决定检验结果:如果一个样本中的14个数据项的方差大于0.005, 则牛产线必须关闭整修。假设博集的数据如下: 表8 产品质量样 3.433.453.43 3.48 3.523.503.39 3.483.41 3.38 3.493.453.513.50 问此时的生产线是否必须关闭?为什么? 10.下面是20个长途电话通话时间的频数分布,计算该数据的平均数、方差和标 准差。 表9 长途电话通话时间的频数分布 通话时间/分频数 通话时间/分频数 47 4 20一23 1 8-11 5 2427 1215 20 16✉19 2 山,某企业工人按日产量分组如下: 单位:(件) 工人按日产量分组 工人数(人) 七月份 八月份 20以下 180 30-40 10s 72 4050 90 120 50-60 90 60以上 合计 360 3600 试计算7、8月份平均每人日产量,并简要说明8月份比7月份平均每人日产量 变化的原因 12.某地甲乙两个农贸市场三种主要蔬菜价格及销售额资料如下: 品种 价值(元/公斤) 销售额(万元) 甲市场 了场 0.30 37. 0.32 40.0 30.0
8 9 195 70 19 39 49 10 95 66 20 35 70 要求:(1)计算两种交易佣金的全距和四分位数间距。 (2)计算两种交易佣金的方差和标准差。 (3)计算两种交易佣金的变异系数。 (4)比较两种交易的成本变异程度。 9.某生产部门利用一种抽样程序来检验新生产出来的产品的质量,该部门使用下 面的法则来决定检验结果:如果一个样本中的 14 个数据项的方差大于 0.005, 则生产线必须关闭整修。假设搜集的数据如下: 表 8 产品质量样本 3.43 3.45 3.43 3.48 3.52 3.50 3.39 3.48 3.41 3.38 3.49 3.45 3.51 3.50 问此时的生产线是否必须关闭?为什么? 10.下面是 20 个长途电话通话时间的频数分布,计算该数据的平均数、方差和标 准差。 表 9 长途电话通话时间的频数分布 通话时间 /分 钟 频数 通话时间 /分 钟 频数 4~7 4 20~23 1 8~11 5 24~27 1 12~15 7 合计 20 16~19 2 11.某企业工人按日产量分组如下: 单位:(件) 工人按日产量分组 工人数(人) 七月份 八月份 20 以下 20~30 30~40 40~50 30 18 78 30 108 72 90 120 50~60 42 90 60 以上 12 30 合计 360 3600 试计算 7、8 月份平均每人日产量,并简要说明 8 月份比 7 月份平均每人日产量 变化的原因。 12.某地甲乙两个农贸市场三种主要蔬菜价格及销售额资料如下: 品种 价值(元/公斤) 销售额(万元) 甲市场 乙市场 甲 乙 0.30 75.0 37.5 0.32 40.0 30.0
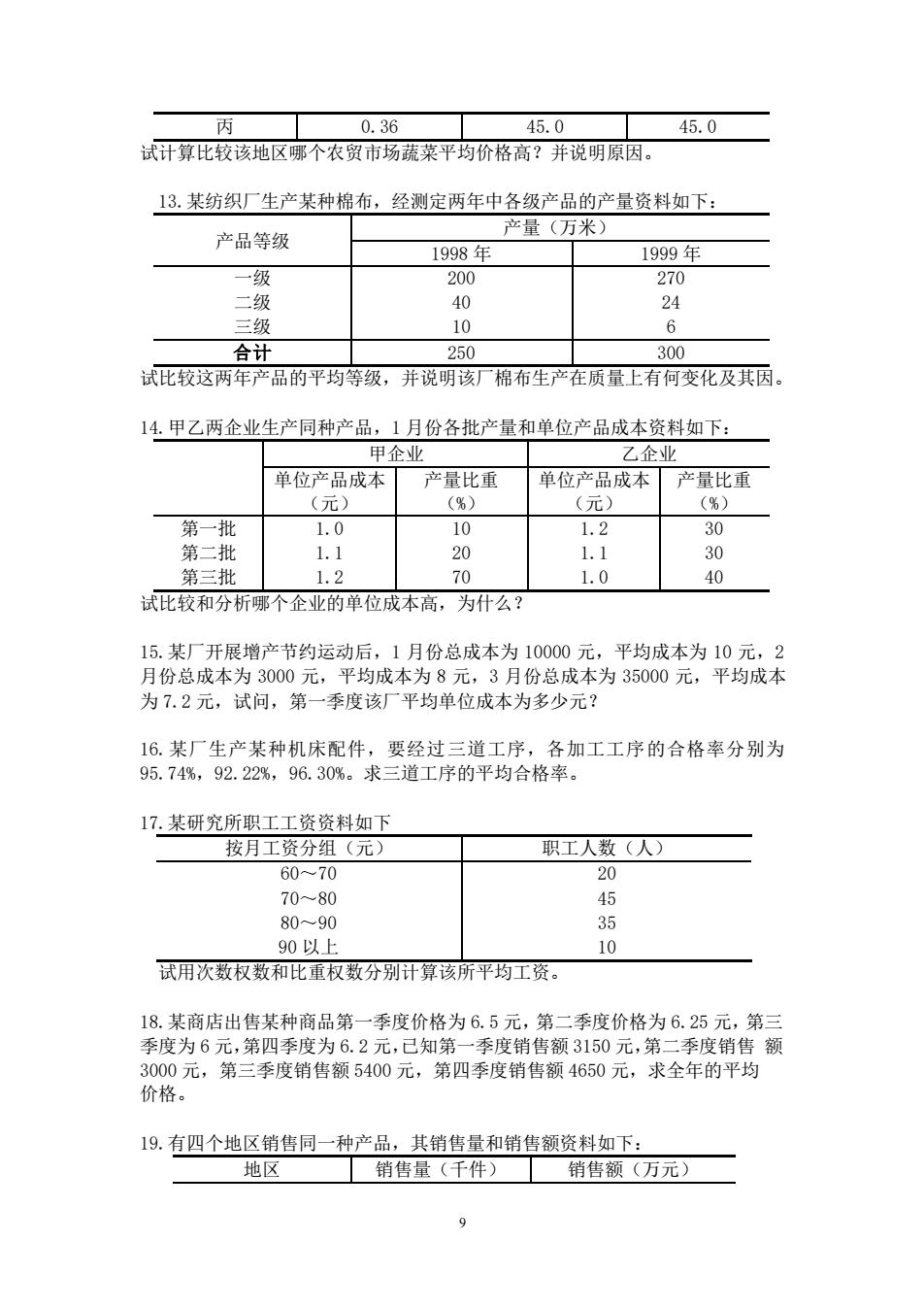
丙 0.36 45.0 45.0 试计算比较该地区哪个农贸市场蔬菜平均价格高?并说明原因。 13.某纺织厂生产某种棉布,经测定两年中各级产品的产量资料如下: 产品等级 产量(万米) 1998年 1999年 一级 200 270 一级 40 24 二成 10 6 合计 250 300 试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。 14.甲乙两企业生产同种产品,1月份各批产量和单位产品成本资料如下 甲企业 乙企业 单位产品成本 产量比重 单位产品成本产量比重 (元) (第) (元) %) 第一批 10 第二批 1.1 20 1.1 30 第三批 1.2 70 1.0 40 试比较和分析哪个企业的单位成本高,为什么? 15.某厂开展增产节约运动后,1月份总成本为10000 平均成本为10元, 月份总成本为3000元,平均成本为8元,3月份总成本为35000元,平均成本 为7.2元,试问,第一季度该厂平均单位成本为多少元? 16.某厂生产某种机床配件,要经过三道工序,各加工工序的合格率分别为 95.74%,92.22%,96.30%。求三道工序的平均合格率 17.某研究所职工工资资料如下 按月工资分组(元) 职工人数(人) 60~70 20 70-80 80-90 35 90以上 10 试用次数权数和比重权数分别计算该所平均工资。 18.某商店出售某种商品第一季度价格为6.5元,第二季度价格为6.25元,第三 季度为6元,第四季度为6.2元,已知第一季度销售额3150元,第二季度销售额 3000元,第三季度销售额5400元,第四季度销售额4650元,求全年的平均 价格。 19.有四个地区销售同一种产品,其销售量和销售额资料如下: 地风 销售量(千件)销售额(万元) 9
9 丙 0.36 45.0 45.0 试计算比较该地区哪个农贸市场蔬菜平均价格高?并说明原因。 13.某纺织厂生产某种棉布,经测定两年中各级产品的产量资料如下: 产品等级 产量(万米) 1998 年 1999 年 一级 二级 200 270 40 24 三级 10 6 合计 250 300 试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。 14.甲乙两企业生产同种产品,1 月份各批产量和单位产品成本资料如下: 甲企业 乙企业 单位产品成本 (元) 产量比重 (%) 单位产品成本 (元) 产量比重 (%) 第一批 第二批 1.0 10 1.2 30 1.1 20 1.1 30 第三批 1.2 70 1.0 40 试比较和分析哪个企业的单位成本高,为什么? 15.某厂开展增产节约运动后,1 月份总成本为 10000 元,平均成本为 10 元,2 月份总成本为 3000 元,平均成本为 8 元,3 月份总成本为 35000 元,平均成本 为 7.2 元,试问,第一季度该厂平均单位成本为多少元? 16.某厂生产某种机床配件,要经过三道工序,各加工工序的合格率分别为 95.74%,92.22%,96.30%。求三道工序的平均合格率。 17.某研究所职工工资资料如下 按月工资分组(元) 职工人数(人) 60~70 20 70~80 45 80~90 35 90 以上 10 试用次数权数和比重权数分别计算该所平均工资。 18.某商店出售某种商品第一季度价格为 6.5 元,第二季度价格为 6.25 元,第三 季度为 6 元,第四季度为 6.2 元,已知第一季度销售额 3150 元,第二季度销售 额 3000 元,第三季度销售额 5400 元,第四季度销售额 4650 元,求全年的平均 价格。 19.有四个地区销售同一种产品,其销售量和销售额资料如下: 地区 销售量(千件) 销售额(万元)

200 00 80 384 试计算各地区平均价格和此种商品在四个地区总的平均价格。 20.某地区20个商店某年第四季度资料: 商品销售计划完 商店数目 实际商品销售 流通费用率 成程度分组(%) 额 (%) (万元) 80~90 45.9 14.8 90100 4 68.4 13.2 100110 8 34.4 12.0 110120 043 110 试计算该地区20个商店平均完成销售计划指标以及总的流通费用率(提示 流通费用率=流通费用额/实际销售额)。 21.某市场上某种蔬菜早市每斤0.25元,中午每斤0.2元,晚市每斤0.1元, 现在早、中、晚各买一元,求平均价格。 22.某商店售货员的工资资料如下: 工资额(元) 售货员人数(人) 375 430 510 37 590 3 690 根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准 差系数。 23.某厂400名职工工资资料如下: 按月工资分组(元) 职工人数(人) 45~5 60 55~65 100 65~75 140 7585 60 8595 合计 400 试根据上述资料计算该厂职工平均工资和标准差。 24.某工厂生产一批零件共10万件 为了解这批产品的质量,采取不重复抽样 的方法抽取1000件进行检查,其结果如下: 使用寿命(小时) 零件数(件)
10 甲 50 200 乙 40 176 丙 60 300 丁 80 384 试计算各地区平均价格和此种商品在四个地区总的平均价格。 20.某地区 20 个商店某年第四季度资料: 商品销售计划完 成程度分组(%) 商店数目 实际商品销售 额 (万元) 流通费用率 (%) 80~90 3 45.9 14.8 90~100 4 68.4 13.2 100~110 8 34.4 12.0 110~120 5 94.3 11.0 试计算该地区 20 个商店平均完成销售计划指标以及总的流通费用率(提示: 流通费用率=流通费用额/实际销售额)。 21.某市场上某种蔬菜早市每斤 0.25 元,中午每斤 0.2 元,晚市每斤 0.1 元, 现在早、中、晚各买一元,求平均价格。 22.某商店售货员的工资资料如下: 工资额(元) 售货员人数(人) 375 4 430 3 510 7 590 3 690 3 根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准 差系数。 23. 某厂 400 名职工工资资料如下: 按月工资分组(元) 职工人数(人) 45~55 60 55~65 100 65~75 140 75~85 60 85~95 40 合计 400 试根据上述资料计算该厂职工平均工资和标准差。 24.某工厂生产一批零件共 10 万件,为了解这批产品的质量,采取不重复抽样 的方法抽取 1000 件进行检查,其结果如下: 使用寿命(小时) 零件数(件)