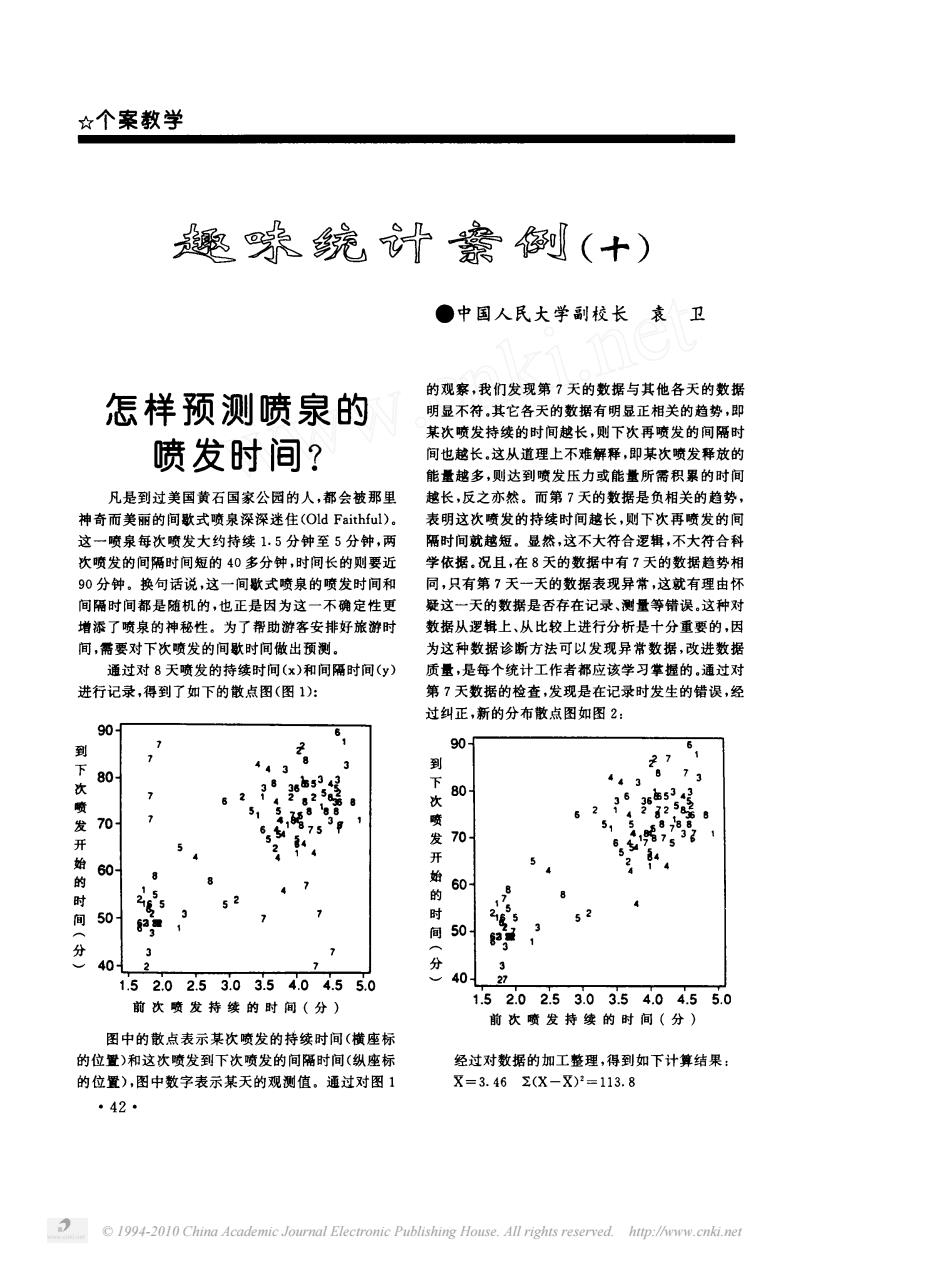
☆个案教学 通味统计案例(十) ●中国人民大学副校长衰卫 的观察,我们发现第?天的数据与其他各天的数据 怎样预测喷泉的 明显不符其它各天的数据有明显正相关的趋势,即 某次喷发持续的时间越长,则下次再喷发的间隔时 喷发时间? 间也越长,这从道理上不难解释,即某次喷发释放的 能量越多,则达到喷发压力或能量所需积累的时间 凡是到过美国黄石国家公园的人,都会被那里 越长,反之亦然。而第?天的数据是负相关的趋势 神奇面警丽的间败式暗良深深米住(O1 d Faithful) 表明这次喷发的持续时间越长,则下次再喷发的间 这一喷泉每次喷发大约持续1.5分钟至5分钟,两 隔时间就短 是然,议不大符合罗, 不大符合刊 次喷发的间隔时间短的40多分钟,时间长的则要近 学依据.况且,在8天的数据中有7天的数据趋势 90分钟,换句话说,这一间歇式喷泉的喷发时间和 同,只有第7天一天的数据表现异常,这就有理由怀 间隔时间都是哺机的,也正是因为 天的数据是否存在记录,测量等错误这种对 增添了喷泉的神秘性。为了帮助 客安排好旅游 数据从逻辑上、从比较上进行分析是十 分重要的,因 间,需要对下次喷发的间歌时间嫩出预剩 为这种数据诊断方法可以发现异常数据,改进数据 通过对8天喷发的持续时间()和同隔时间y) 质量,是每个统计工作者都应该学习掌握的,通过对 进行记录,得到了如下 的散点图(图1): 第7天数据的检克,发现是在记录时发生的错识 ,经 过纠正,新的分布散点图如图2 90 90 到 7 压5 发70 75p 73 60 时 间 0* 52 向50 7 40 152.0253.03.54.04.55.0 40 前次喷发持续的时间(分) 1.52.02.53.03.54.04.55.0 前次喷发持线的时间(分) 图中的散点表示某次喷发的持续时间(横座粉 的位置)和这次喷发到下次喷发的间隔时间(纵座标 经过对数据的加工整理,得到如下计算结果: 的位置),图中数字表示某天的观测值,通过对图1 X=3.462(X-X)2=113.8 *42· 1994-2010 China Academic Journal Electronic Publishing House.All rights reserved.hup://www.cnki.net
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net ☆个案教 学 瘫翅味 统 计 素 例 中 国人 民大 学副 校 长 哀 卫 怎样预 测喷泉 的 喷发时 间 凡是到过美国黄石 国家公 园的人 , 都会被那里 神奇而美丽的间歇式喷泉深深迷住 。 这一喷泉每次 喷发大 约 持续 分钟 至 分钟 , 两 次喷发的间隔时间短 的 多分钟 , 时间长 的则要近 。分钟 。 换句话说 , 这 一间歇式 喷泉的喷发时间和 间隔 时 间都是 随机 的 , 也正是 因为这 一不 确 定 性更 增添 了喷泉的神秘性 。 为了帮助游客安排好旅游时 间 , 需要对下次喷发的间歇 时间做出预测 。 通过对 天喷发的持续时 间 和 间隔时间 进行记录 , 得到 了如下的散点图 图 的观察 , 我 们发现第 天 的数据与其他各天 的数据 明显不符 其它各天 的数据有 明显正相关的趋势 , 即 某次喷发持续 的时间越长 , 则下次再 喷发 的 间隔时 间也越长 。 这从道理上不难解释 , 即某次喷发释放的 能量越 多 , 则达到 喷发压力或能量所需积 累 的时 间 越长 , 反之亦然 。 而第 天的数据是 负相关的趋势 , 表明这次喷发的持续 时间越 长 , 则 下次再喷发的 间 隔时间就越短 。 显然 , 这不大符合逻辑 , 不大符合科 学依据 。 况且 , 在 天的数据 中有 天的数据趋 势相 同 , 只有第 天一天的数据表现异常 , 这就有理 由怀 疑这一天 的数据是否存在记录 、 测量等错误 。 这种对 数据从逻辑上 、 从 比较上进行分析是十分重要的 , 因 为这种数据诊断方法可 以发现异 常数据 , 改进数据 质量 , 是每个统计工作者都应该学 习掌握 的 通过对 第 天数据的检查 , 发现是在记录时发生的错误 , 经 过纠正 , 新的分布散点图如图 字已 呢甘 炸淤 们扮褪 舞 刀 】 门一 月一甲 , 一 丫 甲 前 次 喷 发 持 续 的 时 间 分 下次发始分到喷开时间的︵︶ 矛 日 叹钊‘‘‘,口,﹃ 刁气﹂ , 卜 。 护 味卜, 女 通”, 分始时间发开的次喷下到︶︵ 前 次 喷 发 持 续 的 时 间 分 图 中的散 点表示 某次喷发 的持续 时间 横座标 的位置 和这次喷发到 下次喷发的间隔时间 纵座标 的位置 , 图中数字表示某天的观测值 。 通过对 图 。 · 经过对数据 的加工整理 , 得到 如下计算结果 艺 一
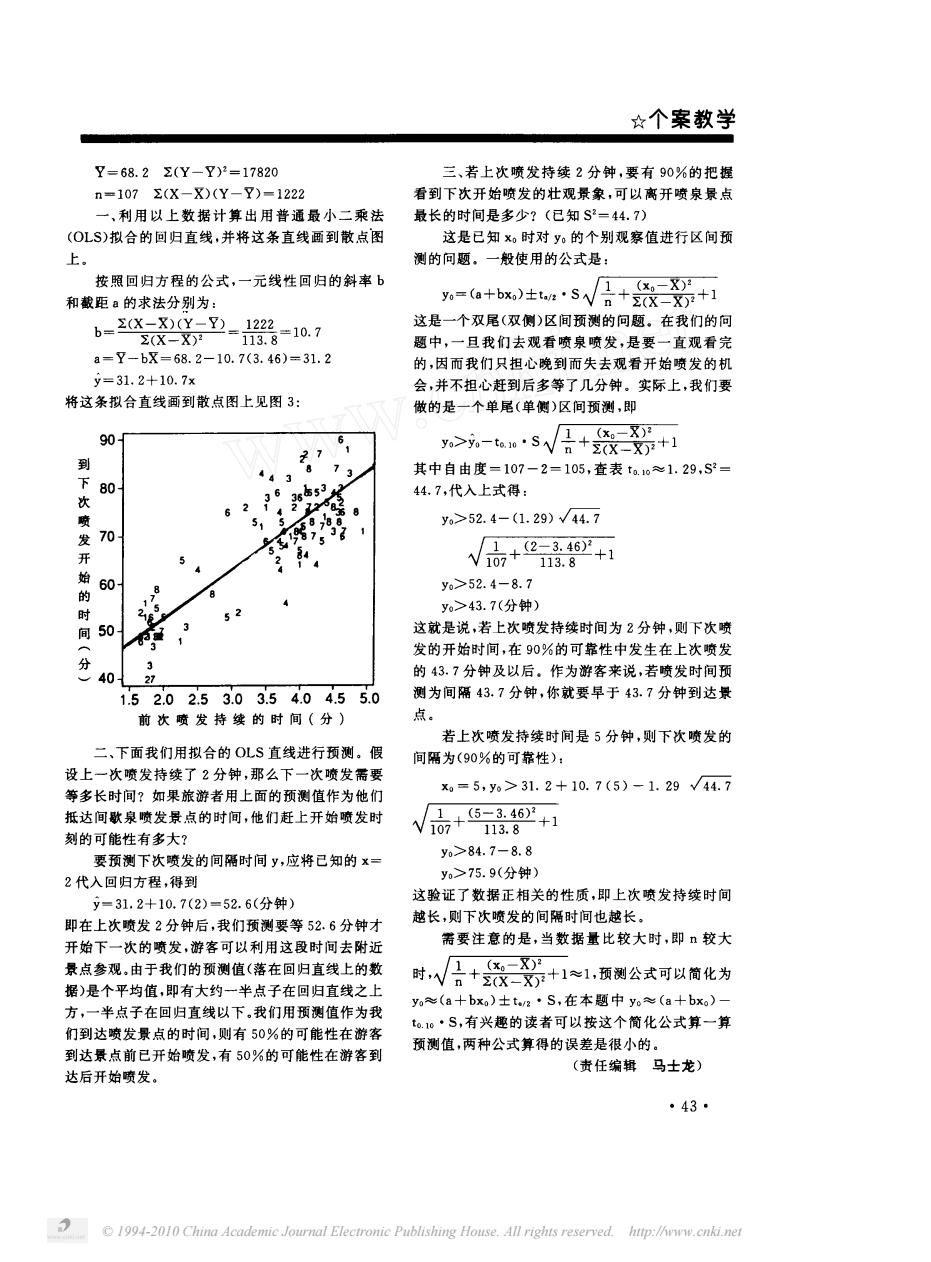
☆个案教学 Y=68.2Σ(Y-Y2=17820 三、若上次喷发持续2分钟,要有90⅓的把握 m=107yX-X)y_7)-1222 看到下次开始喷发的壮观景象,可以离开喷泉景点 一,利用以上数据计算出用普通最小二乘法 最长的时间是多少?(已知S=44.7) (OLS)拉合的回归直线,并将这条直线画到散点图 这是已知x。时对。的个别观襄值进行区间陌 上 测的问题。一般使用的公式是: 按照回归方程的公式,一元性回归的斜率b 和截距。的求法分别为 y%=(a+bx)士aS√合+二3+1 这是一个双尾(双侧)区间预测的问题,在我们的同 题中,一且我们去观看喷泉喷发,是要一直观看完 82-10.7(3.46=31.2 的,因而我们只担心晚到而失去观看开始喷发的机 会,并不担心赶到后多等了几分钟,实际上,我们要 散点图上见图3 做的是一个单尾(单侧)区间预测,即 90 >-t层++ 到 4 73 其中自由度=107-2=105,查表t16≈1.29,S2= 36s53 44.7,代入上式得: 58 y>52.4-(1.29V44.7 √+2+ >52,4-8.7 3.7(分钟 50 这就是说,者上次喷发持续时间为2分钟,则下次 发的开始时间,在90%的可靠性中发生在上次喷发 的43.7分钟及以后。作为游客来说,若喷发时间开 1520253.03.54.04.55.0 测为间隔43.7分钟,你就要早于43.7分钟到达景 前次喷发持续的时间(分) 若上次喷发持续时间是5分钟,则下次喷发的 二下而我们用拟合的O儿S直线井行稻测。假 间隔为(90%的可常性): 母上一次喷发持缕了2分轴,那么下一次喷发需 等多长时间?如果旅游者用上面的预测值作为他们 x0=5,y>31.2+10.7(5)-1.29√44.7 抵达敢泉喷发景点的时间,他们赶上开始喷发时 √+5-3462+1 刻的可能性有多大? 药湖 次喷发的间隔时间y,应将已知的x %>84.7 2代 回归方程,得到 31.2+10.72=52.6(分钟 的性质,即上次喷发持绞时间 即在上次喷发2分钟后,我们 要等52.6分钟才 越长,则下次喷发的间隔时间也越长 始下一次的喷发 段时 希要注意的是,当数据量比较大时,即较大 参观,由于我 们 (落在回 时,层十最十1,溪装公式可以黄化为 我们用 yo(a+bx S,在本题中y(a+bx) 值作为 ,有兴趣的 读者可飞 值,两种公式算的 化公式算 点 可能性在游 开始喷发,有50%的可能性在游客到 差是很小 (责任编辑 马士龙 43 1994-2010 China Academic Journal Electronic Publishing House.All rights reserved.hup:/ww.cnkinet
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net ☆个案教 学 艺 一 艺 一 一 亨 一 、 利 用 以 上 数 据计 算 出用 普 通 最 小 二 乘 法 拟合 的 回归直线 , 并将这条直线画到 散点 图 上 。 按 照 回 归方程 的公式 , 一 元 线性 回 归的斜率 和截距 的求法分别为 三 、 若上 次 喷发持续 分 钟 , 要 有 写的把 握 看到 下次开始喷发 的壮观景象 , 可 以 离 开 喷泉景 点 最长的时间是多少 已知 一 这是 已 知 。 时对 。 的个别观察值进行 区 间预 测 的间题 。 一般使用的公式是 。 十 。 士 。 。 一 又 人 —十 二丁 笼于 飞 十 汤 气人 一 入 少 “ 乏 一 一 艺 一 二 一 又 一 将这条拟合直线画到 散点图上见 图 这是一个双尾 双侧 区 间预测 的问题 。 在我 们的问 题 中 , 一 旦 我 们去观 看 喷泉 喷 发 , 是 要 一 直 观看 完 的 , 因而 我 们只担心 晚到 而 失去观看开 始 喷发 的机 会 , 并不担心赶到后 多等 了几分钟 。 实际上 , 我们要 做 的是一个单尾 单侧 区 间预测 , 即 。 。一 。 。 一 又 人 甲 , 十 芬忿节 , 齐 二 十 石 气人 一 入 其 中 自由度 一 , 查 表 , 。 、 , , , 代入上式得 。 一 丫丽二万 沪 , 声尹 ‘ 大 户叮呀 任 下 几 掌督 ‘ ’‘ ‘ 入 尹 , 一 到下次喷发开始时分的间︵︶ 前 次 喷 发 持 续 的 时 间 分 二 、 下面我们用拟合 的 直线进行预测 。 假 设上一次 喷发持续 了 分钟 , 那么 下 一 次喷发需要 等多长 时间 如果旅游者用 上面的预测值作为他们 抵达 间歇泉 喷发景 点的时 间 , 他们赶上开 始喷发 时 刻的可能性有多大 要预测下次喷发的间隔时间 , 应将 已知 的 代入 回 归方程 , 得到 夕 分钟 即在上次喷发 分钟后 , 我们预测要等 分钟才 开始下一次的喷发 , 游 客可 以 利用这段 时 间去附近 景点参观 。 由于 我们的预测值 落在 回归直线上的数 据 是个平均值 , 即有大约一半点子在 回归直线之上 方 , 一半点子在 回归直线 以下 。 我们用预测值作为我 们到达喷发景点的时间 , 则有 的可能性在游 客 到达景点前 已开始喷发 , 有 的可能性在 游客到 达后开始喷发 。 。 一 。 分钟 这就是说 , 若上次喷发持续时间为 分钟 , 则 下次 喷 发的开始时间 , 在 的可靠性 中发生在 上 次 喷发 的 分钟及 以后 。 作为游客来说 , 若喷发 时间预 测 为间隔 分钟 , 你就要早 于 分钟到 达景 点 。 若上次 喷发持续 时间是 分 钟 , 则 下次 喷发 的 间隔为 的可靠性 。 , 。 一 、石不下 。 一 。 分钟 这验证 了数据正相关的性 质 , 即上次 喷发持续 时 间 越长 , 则下次喷发的间隔时间也越长 。 需要 注 意 的是 , 当 数据量 比较大 时 , 即 较 大 。 一 又 “ 盯 , 人 一 十 二二二二 , 毛六下 十 乙 气人 一 人 少 、 , 预测 公式可 以 简化为 。 、 。 士 。 , · , 在 本 题 中 。 、 。 一 。 · , 有兴趣的读 者可 以 按这个 简化公式算一 算 预测值 , 两种公式算得的误差是很 小的 责任编辑 马士龙