不良贷款因素分析 一家大型商业银行在多个地区设有分行,其业务主要是进行基础设施建设、国家重点项目建设、 固定资产投资等项目的贷款。近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提 高,这给银行业务的发展带来较大压力。为了弄清楚不良贷款形成的原因,希望利用银行业务的有 关数据做些定量分析,以便找出控制不良贷款的办法。2005年该银行所属的25家分行的有关业务数 据如下表所示。 某商业银行2005年的主要业务数据表 分行 不良贷款 各项贷款余额 本年累计应收 贷款项目 本年固定资产投资 (亿元) (亿元) 贷款(亿元) 个数(个加额(亿元)社 1.2 70.6 7.7 54.7 14 1146 207 17 938 51 176.3 86 18 766 35 83.9 8.1 0 18.5 8.2 202.8 17.5 20 66.3 6 20 105 34 40 19 110.7 11.7 17 23.6 127 1889 27.9 8 46.9 9 1.3 99.6 2.6 11 56.1 10 20 761 101 16 67.6 11 0.6 678 31 12 459 12 4.3 135.6 12.1 25 79.8 13 1.1 67.7 6.9 16 25.9 14 38 177.9 136 27 120.1 105 2666 165 35 1499 16 3.3 82.6 9.8 16 32.7 17 0.5 17.9 1.5 4 45.6 18 07 767 68 13 286 1.3 27.8 5.9 16.8 20 143.1 8.1 29 67.8 21 119 3716 17.7 34 167.2 19 002 47 12 47.8 1.5 112.9 11.2 16 70.2 24 7.3 199.8 16.7 18 43.1 25 3.6 105.7 12.9 12 100.2 讨论题: (1)分别绘制不良贷款与贷款余额、应收贷款、贷款项目数、固定资产投资额之间的散点图,并 分析其关系。若有关系,它们之间是一种什么样的关系?关系强度如何?
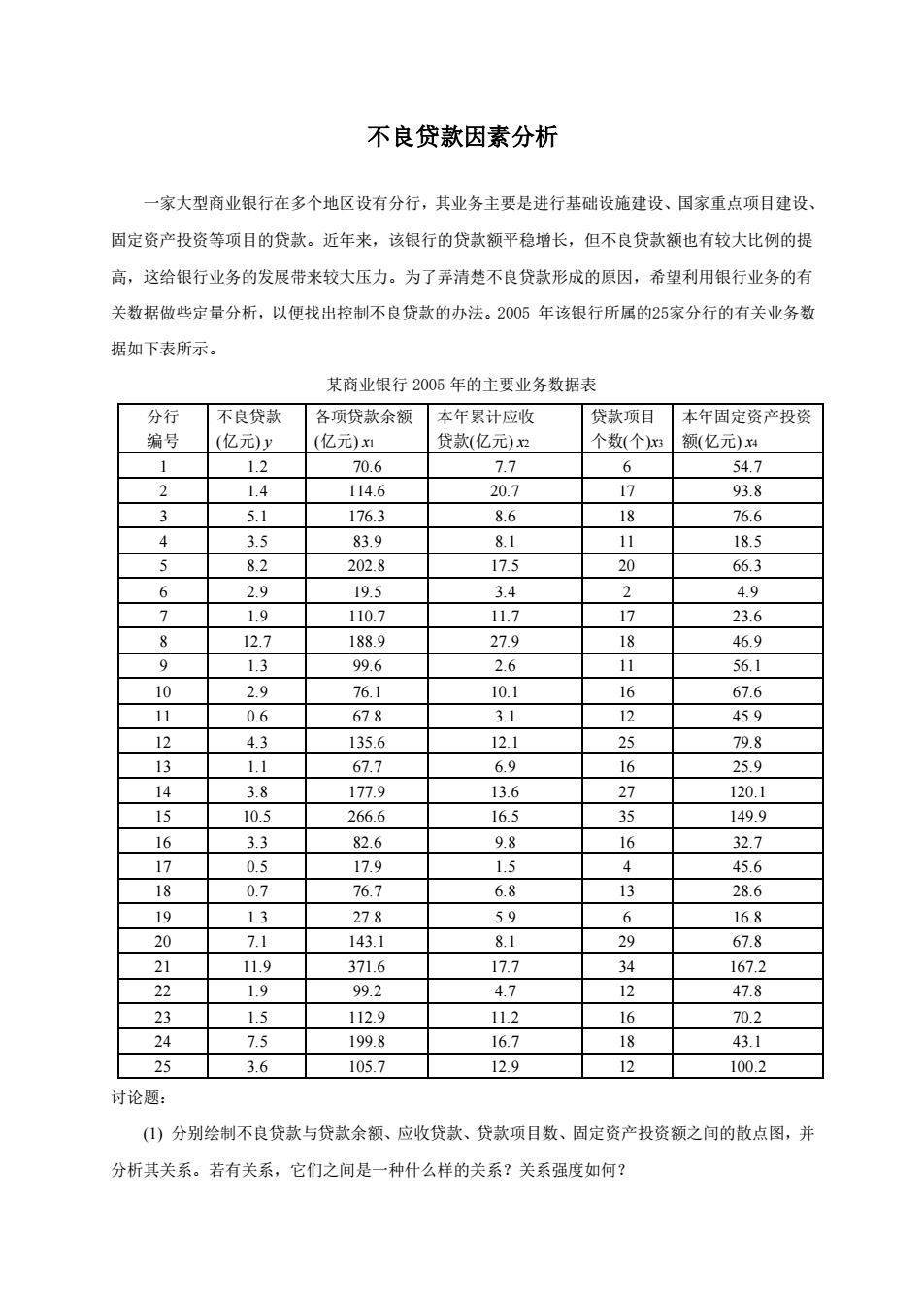
不良贷款因素分析 一家大型商业银行在多个地区设有分行,其业务主要是进行基础设施建设、国家重点项目建设、 固定资产投资等项目的贷款。近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提 高,这给银行业务的发展带来较大压力。为了弄清楚不良贷款形成的原因,希望利用银行业务的有 关数据做些定量分析,以便找出控制不良贷款的办法。2005 年该银行所属的25家分行的有关业务数 据如下表所示。 某商业银行 2005 年的主要业务数据表 分行 编号 不良贷款 (亿元) y 各项贷款余额 (亿元) x1 本年累计应收 贷款(亿元) x2 贷款项目 个数(个)x3 本年固定资产投资 额(亿元) x4 1 1.2 70.6 7.7 6 54.7 2 1.4 114.6 20.7 17 93.8 3 5.1 176.3 8.6 18 76.6 4 3.5 83.9 8.1 11 18.5 5 8.2 202.8 17.5 20 66.3 6 2.9 19.5 3.4 2 4.9 7 1.9 110.7 11.7 17 23.6 8 12.7 188.9 27.9 18 46.9 9 1.3 99.6 2.6 11 56.1 10 2.9 76.1 10.1 16 67.6 11 0.6 67.8 3.1 12 45.9 12 4.3 135.6 12.1 25 79.8 13 1.1 67.7 6.9 16 25.9 14 3.8 177.9 13.6 27 120.1 15 10.5 266.6 16.5 35 149.9 16 3.3 82.6 9.8 16 32.7 17 0.5 17.9 1.5 4 45.6 18 0.7 76.7 6.8 13 28.6 19 1.3 27.8 5.9 6 16.8 20 7.1 143.1 8.1 29 67.8 21 11.9 371.6 17.7 34 167.2 22 1.9 99.2 4.7 12 47.8 23 1.5 112.9 11.2 16 70.2 24 7.5 199.8 16.7 18 43.1 25 3.6 105.7 12.9 12 100.2 讨论题: (1) 分别绘制不良贷款与贷款余额、应收贷款、贷款项目数、固定资产投资额之间的散点图,并 分析其关系。若有关系,它们之间是一种什么样的关系?关系强度如何?

(②)建立不良贷款与贷款余额、累计应收贷款、贷款项目数、固定资产投资额等因素的多元线性 回归方程,并解释各回归系数的实际意义。 (3)在不良贷款的总变差中,被估计的回归方程所解释的比例是多少? (4)根据建立的回归方程,对回归方程线性关系的显著性及各回归系数的显著性进行检验( -0.05)。 (5)当回归模型中两个或两个以上的自变量彼此相关时,我们就说存在多重共线性。在回归分 析中存在多重共线性将会产生某些问题,如可能会给回归的结果造成混乱,甚至会把分析引入歧途: 可能对参数估计值的正负号产生影响,特别是阝的正负号有可能同我们预期的正负号相反。试分析 建立的回归方程是否存在多重共线性,你认为哪些因素应该从模型中剔除。 (6)若贷款余额x,=100、累计应收贷款x:=10、贷款项目个数x,=15和固定资产投资额x,=60,根 据建立的回归方程,求不良贷款(y)的95%置信区间和预测区间
(2) 建立不良贷款与贷款余额、累计应收贷款、贷款项目数、固定资产投资额等因素的多元线性 回归方程,并解释各回归系数的实际意义。 (3)在不良贷款的总变差中,被估计的回归方程所解释的比例是多少? (4)根据建立的回归方程,对回归方程线性关系的显著性及各回归系数的显著性进行检验(a =0.05)。 (5)当回归模型中两个或两个以上的自变量彼此相关时,我们就说存在多重共线性。在回归分 析中存在多重共线性将会产生某些问题,如可能会给回归的结果造成混乱,甚至会把分析引入歧途; 可能对参数估计值的正负号产生影响,特别是 i ˆ 的正负号有可能同我们预期的正负号相反。试分析 建立的回归方程是否存在多重共线性,你认为哪些因素应该从模型中剔除。 (6) 若贷款余额x 1 =100、累计应收贷款x2 =10、贷款项目个数x3 =15 和固定资产投资额x4 =60,根 据建立的回归方程,求不良贷款( y )的95%置信区间和预测区间