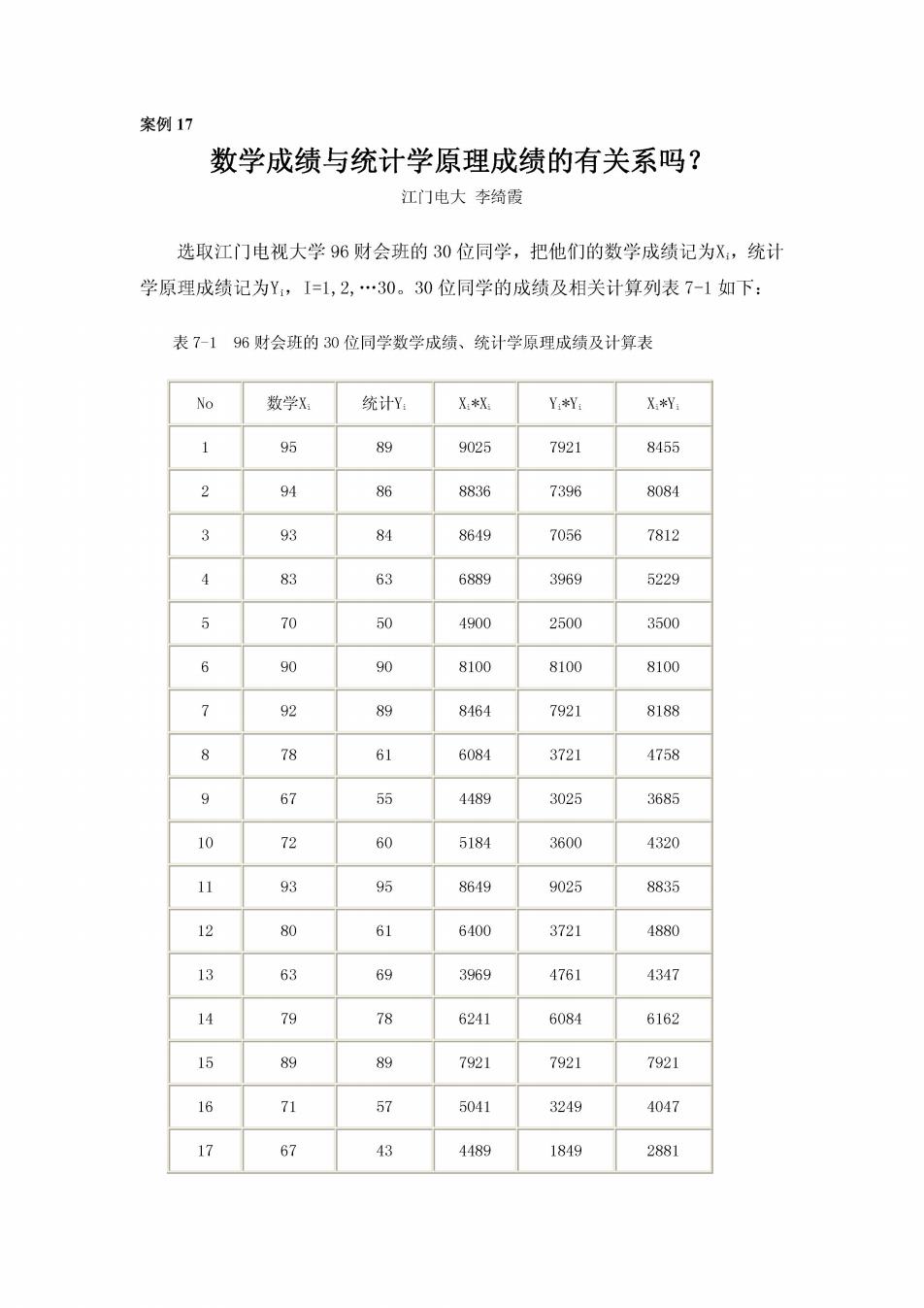
案例17 数学成绩与统计学原理成绩的有关系吗? 江门电大李绮陵 选取江门电视大学96财会班的30位同学,把他们的数学成绩记为X,统 学原理成绩记为Y,I=1,2,.30.30位同学的成绩及相关计算列表7-1如下: 表7-196财会班的0位同学数学成绩、统计学原理成绩及计算表 No 数学X 统计Y X.*X. YY.X.*Y. 95 89 9025 7921 8455 94 86 8836 7396 8084 9 84 8649 7056 7812 63 6889 3969 5229 70 50 4900 2500 3500 90 90 8100 8100 8100 89 8464 7921 8188 78 61 6081 3721 4758 67 55 4489 3025 3685 10 72 60 5184 3600 4320 95 8649 9025 8835 12 80 61 6400 3721 4880 13 63 69 3969 4761 4347 14 78 6241 6084 6162 15 89 89 7921 7921 7921 16 71 57 5041 3249 4047 17 67 43 4489 1849 2881
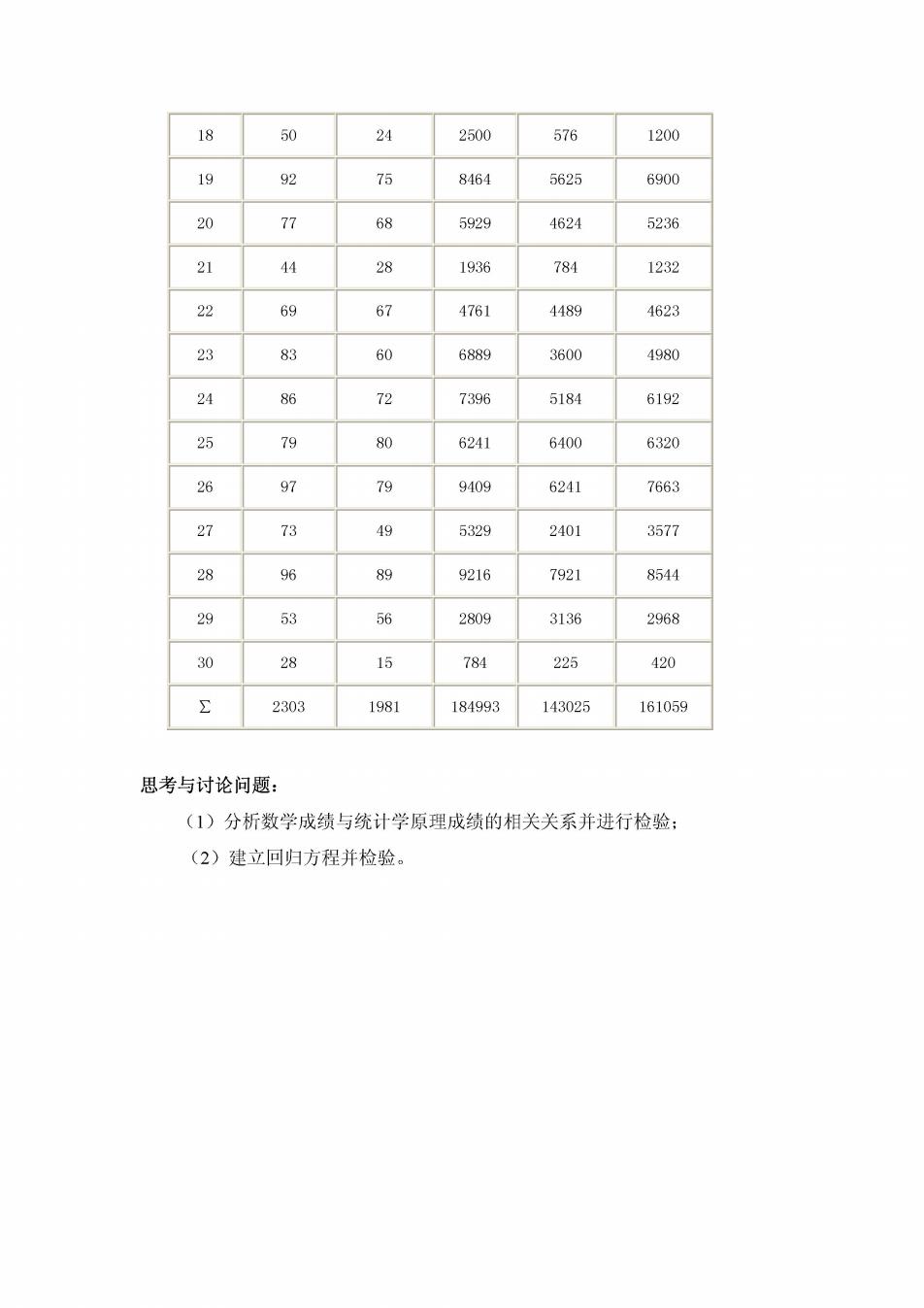
24 2500 576 1200 75 8464 5625 6900 68 5929 4624 5236 44 28 1936 784 1232 2 69 67 4761 4489 4623 23 83 60 6889 3600 4980 24 86 72 7396 5184 6192 25 79 80 6241 6400 6320 26 97 79 9409 6241 7663 27 73 49 5329 2401 3577 28 96 89 9216 7921 8544 29 53 56 2809 3136 2968 30 28 784 225 420 2303 1981 184993 143025 161059 思考与讨论问题: (1)分析数学成绩与统计学原理成绩的相关关系并进行检验: (2)建立回归方程并检验

数学是一门基础课,比较枯燥、抽象,特别是高等数学的一些内容,学生学起来觉得吃力 例如日常生活中很少要用到这些深奥的数学知识。为什么要学好数学呢?经过调查,发现数 学成绩好的学生,其它课程的成绩大多数也好,特别是与数学联系比较密切的课程,如统计 学原理、计算机等。为了找出学生的联系,我们利用统计学中相关分析的方法,找出它们的 内在联系。 标准差6 标准差 相关系数 现在用相关系数的显著性验证从总体上说,数学与统计学原理是否存在相关。 检验的步骤 1)提出假设 H:H 2)选择检验统计量并计算其值 由于n-302.763=,则P>0.01,应在 0.01显若性水平上拒绝零假设, 而接受备择假设。其结论为:样本的0.898与总体零相关 有极其显著性差异。从总体上说,数学分数与统计学原理分数存在正相关。也就是说,大多 数学生的数学成绩好的,他的统计成绩也好。 为了进一步说明数学成绩与统计学成绩的关系,下面作出由数学成绩X估计统计学原理成 绩Y的线性回归方程:Y=a+bX 利用两个样本的标准差及相关系数计算: b= a= 所以其线性回归方和为:Y=.1841+1.10X 由X估计Y回归系数的标准误差为: S=

现检验回归系数b=1.10的显著性。 1)提出假设 H 2)计算检验统计量的值 回归系数的抽样分布呈分布,其检验统计量为 t= -10.78 3)确定检验的形式 采用双侧检验。 4)统计决断 根据自由度=m-2=30-2=28,查t值表找到t=2.763,由于t=10.78>2.763.则P0.01,应在 0.01显若性水平上拒绝零假设,而接受备择假设。其结论为:学生的数学成绩与统计学原理 成绩存在线性关系 综上分析,使我们了解到数学是其它学科的基础,学好数学,对学习其它课程大有帮助