
第3章概率与抽样分布 Probability and Sampling Distributions
第3章 概率与抽样分布 Probability and Sampling Distributions

Section 3.1 Random Variables 随机变量
Section 3.1 Random Variables 随机变量

一、频率与概率frequency and probability 事件的实际发生率称为频率。设在相同 条件下,独立重复进行n次试验,事件A出现 f次,则事件A出现的频率为f升n。 概率:随机事件发生的可能性大小,用 大写的P表示;取值[0,1]
事件的实际发生率称为频率。设在相同 条件下,独立重复进行n次试验,事件A出现 f 次,则事件A出现的频率为f/n。 概率:随机事件发生的可能性大小,用 大写的P 表示;取值[0,1]。 一、频率与概率frequency and probability
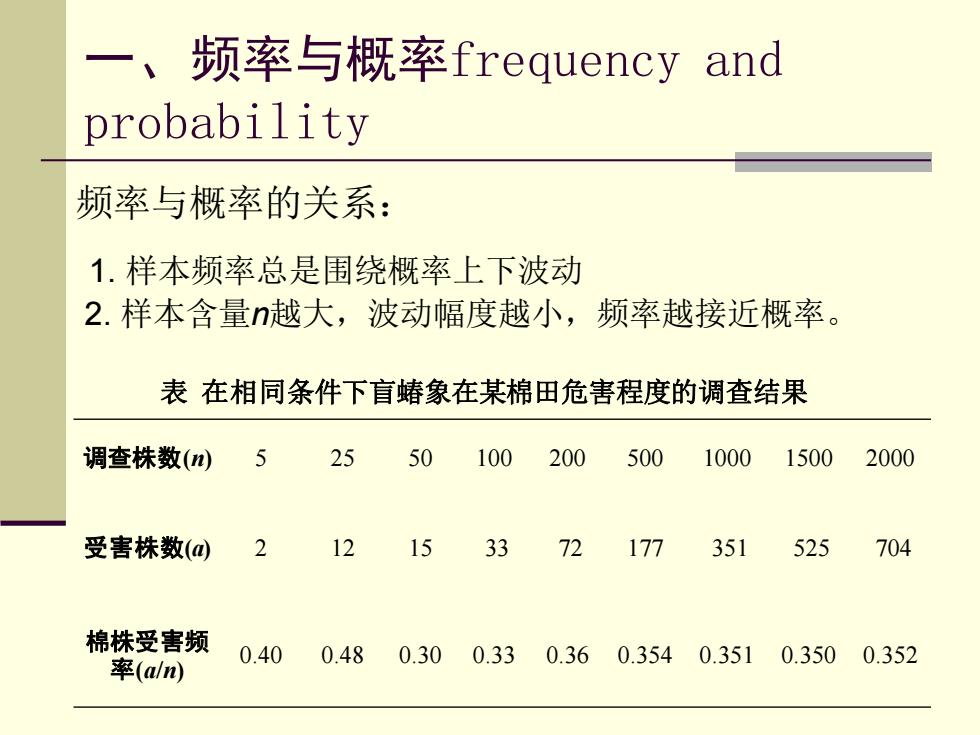
一、频率与概率frequency and probability 频率与概率的关系: 1.样本频率总是围绕概率上下波动 2.样本含量n越大,波动幅度越小,频率越接近概率。 表在相同条件下盲蝽象在某棉田危害程度的调查结果 调查株数(n) 5 25 50100 200 500 1000 1500 2000 受害株数(@ 2 12 153372177 351 525 704 棉株受害频 率(alnm) 0.400.480.300.330.360.3540.3510.3500.352
1. 样本频率总是围绕概率上下波动 2. 样本含量n越大,波动幅度越小,频率越接近概率。 频率与概率的关系: 调查株数(n) 5 25 50 100 200 500 1000 1500 2000 受害株数(a) 2 12 15 33 72 177 351 525 704 棉株受害频 率(a/n) 0.40 0.48 0.30 0.33 0.36 0.354 0.351 0.350 0.352 表 在相同条件下盲蝽象在某棉田危害程度的调查结果 一、频率与概率frequency and probability

一、 频率与概率frequency and probability 小概率原理 若事件A发生的概率较小,如小于0.05或0.01,则认为 事件A在一次试验中不太可能发生,这称为小概率事件实际 不可能性原理,简称小概率原理。这里的0.05或0.01称为小 概率标准,农业试验研究中通常使用这两个小概率标准
一、频率与概率frequency and probability 小概率原理 若事件A发生的概率较小,如小于0.05或0.01,则认为 事件A在一次试验中不太可能发生,这称为小概率事件实际 不可能性原理,简称小概率原理。这里的0.05或0.01称为小 概率标准,农业试验研究中通常使用这两个小概率标准

二、随机变量 >用以记录随机试验结果(outcome))的变量,称 为随机变量(random variable),用大写英文 字母X,Y等代表。 >随机变量X的概率分布,表达X的可能取值 和取这些值的概率规则
二、随机变量 ➢ 用以记录随机试验结果(outcome)的变量,称 为随机变量(random variable),用大写英文 字母X, Y 等代表。 ➢ 随机变量X的概率分布,表达 X 的可能取值 和取这些值的概率规则

二、随机变量 离散型和连续型随机变量 >随机变量的可能取值是离散的数字,如计数型或分类 型等,称为离散型随机变量(discrete random variable)。 ■{0,1,9}。 ·20次实验中成功的次数,二项式分布。 >随机变量的可能取值是某一实数的区间,如“大于0” 或“-22之间”等,称为连续型随机变量 (continuous random variable). ■正态随机变量
离散型和连续型随机变量 ➢ 随机变量的可能取值是离散的数字,如计数型或分类 型等,称为离散型随机变量(discrete random variable)。 ▪ {0, 1,., 9} 。 ▪ 20次实验中成功的次数, 二项式分布。 ➢ 随机变量的可能取值是某一实数的区间,如“大于0” 或“-2~2之间”等,称为连续型随机变量 (continuous random variable)。 ▪ 正态随机变量 二、随机变量

三、离散型随机变量的概率分布 >列出离散型随机变量X的所有可能取值 >列出随机变量取这些值的概率 >通常用下面的表格来表示 X=xi X12.n P(X=x)-Pi P1yP2y.yPn >P(仪=x;)=p:称为离散型随机变量的概率函数 p,≥O
三、离散型随机变量的概率分布 X = xi x1 ,x2,. ,xn P(X =xi )=pi p1 ,p2,. ,pn 1 0 1 i n i i p p = = ➢ 列出离散型随机变量X的所有可能取值 ➢ 列出随机变量取这些值的概率 ➢ 通常用下面的表格来表示 ➢ P(X =xi)=pi称为离散型随机变量的概率函数

四、连续型随机变量的概率密度 >若观察资料数量够大,则直方图(组数适当增 加)的整体形态可用一近似的平滑曲线显示。 >直方图中纵轴改为次数比例,则该平滑曲线 称为密度曲线(density curve)
四、连续型随机变量的概率密度 ➢ 若观察资料数量够大,则直方图(组数适当增 加)的整体形态可用一近似的平滑曲线显示。 ➢ 直方图中纵轴改为次数比例,则该平滑曲线 称为密度曲线(density curve)
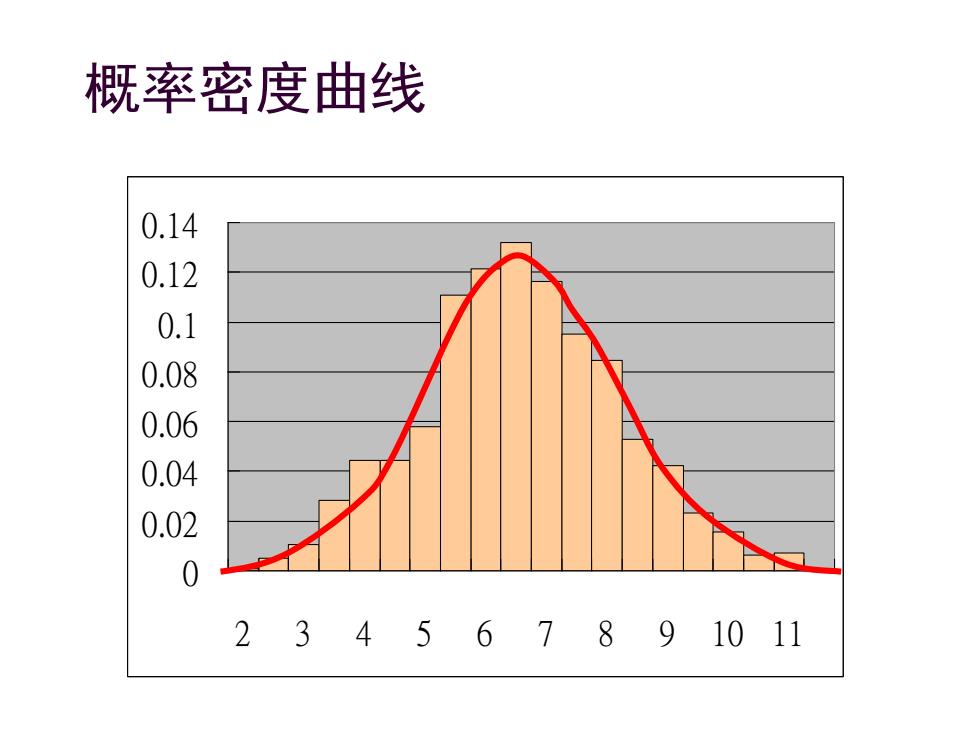
概率密度曲线 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 234567891011
概率密度曲线 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 2 3 4 5 6 7 8 9 10 11