
第7章方差分析 Analysis of Variance (ANOVA)
第7章 方差分析 Analysis of Variance (ANOVA)

Section 7.1 Principle of ANOVA 方差分析的基本原理
Section 7.1 Principle of ANOVA 方差分析的基本原理

什么是方差分析 > ANOVA由英国统计 Ronald Fisher 学家R.A.Fisher首 创,为纪念Fisher 以F命名,故方差 分析又称F检验 (F test)。用于 推断多个总体均数 有无差异
什么是方差分析 ➢ANOVA 由英国统计 学家R.A.Fisher首 创,为纪念Fisher 以F命名,故方差 分析又称 F 检验 (F test)。用于 推断多个总体均数 有无差异
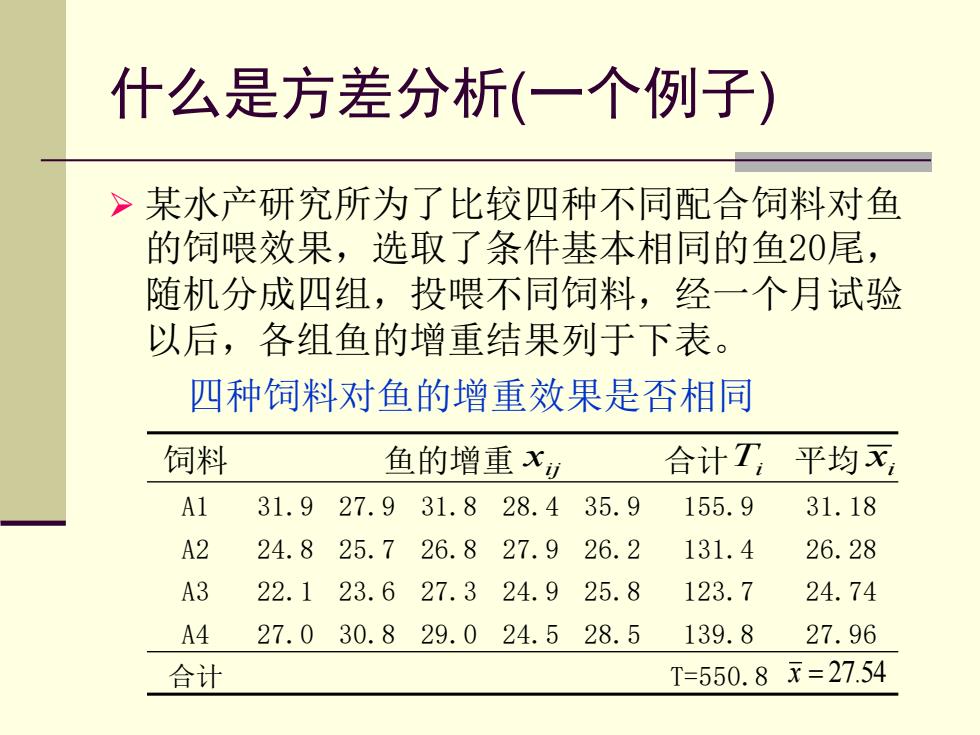
什么是方差分析(一个例子) >某水产研究所为了比较四种不同配合饲料对鱼 的饲喂效果,选取了条件基本相同的鱼20尾, 随机分成四组,投喂不同饲料,经一个月试验 以后,各组鱼的增重结果列于下表。 四种饲料对鱼的增重效果是否相同 饲料 鱼的增重x 合计T 平均 A1 31.927.931.828.435.9 155.9 31.18 A2 24.825.726.827.926.2 131.4 26.28 A3 22.123.627.324.925.8 123.7 24.74 A4 27.030.829.024.528.5 139.8 27.96 合计 T=550.8x=27.54
什么是方差分析(一个例子) ➢ 某水产研究所为了比较四种不同配合饲料对鱼 的饲喂效果,选取了条件基本相同的鱼20尾, 随机分成四组,投喂不同饲料,经一个月试验 以后,各组鱼的增重结果列于下表。 ▪ 四种饲料对鱼的增重效果是否相同 饲料 鱼的增重 合计 平均 A1 31.9 27.9 31.8 28.4 35.9 155.9 31.18 A2 24.8 25.7 26.8 27.9 26.2 131.4 26.28 A3 22.1 23.6 27.3 24.9 25.8 123.7 24.74 A4 27.0 30.8 29.0 24.5 28.5 139.8 27.96 合计 T=550.8 x = 27.54 xij Ti xi

什么是方差分析(例子分析) > 一个因素(factor):饲料 > 四个水平(1eve1):A1、A2、A3、A4 > 每一个水平重复试验四次 > 设μ1为饲料A1的平均增重,2为饲料A2的平均 增重,u3为饲料A3的平均增重,设u4为饲料A4 的平均增重,检验四种饲料对鱼的增重效果 是否相同,也就是检验下面的假设 6:41=2=3=4 H:41,2,山3,4不全相等 检验上述假设所采用的方法就是方差分析
什么是方差分析(例子分析) ➢ 一个因素(factor):饲料 ➢ 四个水平(level):A1、A2、A3、A4 ➢ 每一个水平重复试验四次 ➢ 设1为饲料A1的平均增重,2为饲料A2的平均 增重,3为饲料A3的平均增重,设4为饲料A4 的平均增重,检验四种饲料对鱼的增重效果 是否相同,也就是检验下面的假设 H0 : 1 = 2 = 3 = 4 HA: 1 , 2 , 3 , 4不全相等 ➢ 检验上述假设所采用的方法就是方差分析

方差分析的基本思想 >将所有测量值间的总变异按照其变异的来源分 解为多个部份,然后进行比较,评价由某种因 素所引起的变异是否具有统计学意义
方差分析的基本思想 ➢ 将所有测量值间的总变异按照其变异的来源分 解为多个部份,然后进行比较,评价由某种因 素所引起的变异是否具有统计学意义
离均差平方和的分解 组间变异 组内变异 总变异
离均差平方和的分解 组间变异 总变异 组内变异

离均差平方和的分解(例子分析) >共有三种不同的变异 ·总变异(Total variation):全部测量值x与总 均数x=27.54间的差异 ■组间变异(between group variation ):各组 的均数x,与总均数x=27.54间的差异 ·组内变异(within group variation):每组的每 个测量值X,与该组均数x,的差异 >用离均差平方和(sum of squares of deviations from mean,SS)反映变异的大小
离均差平方和的分解(例子分析) ➢ 共有三种不同的变异 ▪ 总变异(Total variation):全部测量值 与总 均数 间的差异 ▪ 组间变异( between group variation ):各组 的均数 与总均数 间的差异 ▪ 组内变异(within group variation ):每组的每 个测量值 与该组均数 的差异 ➢ 用离均差平方和(sum of squares of deviations from mean,SS)反映变异的大小 x = 27.54 xij x i x = 27.54 xij x i

总变异:所有测量值之间总的变异程度 >计算公式 5-客2-c =2x-C=(nk-l)s好 nk i,1 Vr=nk-1 n (x)2 i=1i=1 T2 >矫正系数 C= nk nk
总变异:所有测量值之间总的变异程度 ➢ 计算公式 ➢ 矫正系数 ( ) 2 2 1 1 1 1 2 2 , 1) k n k n ij ij i j i j nk ij T i j SS x x x C x C s = = = = = − = − = − − T =(nk 2 2 1 1 ( ) k n ij i j x T C nk nk = = = = T = − nk 1

组间变异:各组均数与总均数的 离均差平方和 >计算公式 5双,=立(怎=至-C i=l V=k-1 SS反映了各组均数x:的变异程度 组间变异=①随机误差+②处理因素效应
组间变异:各组均数与总均数的 离均差平方和 ➢ 计算公式 2 2 1 1 ( ) k k i i i i T SS n x x C = = n t = − = − = −k 1 t SSt反映了各组均数 的变异程度 组间变异=①随机误差+②处理因素效应 x i