
第十二章 回归设计 12.1 回归设计的基本概念 12.2 一次回归正交设计 12.3 二次回归的中心组合设计 12.4 二次回归正交设计 12.5 二次回归旋转设计
第十二章 回归设计 12.1 回归设计的基本概念 12.2 一次回归正交设计 12.3 二次回归的中心组合设计 12.4 二次回归正交设计 12.5 二次回归旋转设计

12.1 回归设计的基本概念 回归设计(也称为响应曲面设计) 目的是寻找试验指标与各因子间的定量规律, 考察的因子都是定量的 。 它是在多元线性回归的基础上用主动收集数据的方法获 得具有较好性质的回归方程的一种试验设计方法。 本章主要介绍Box的回归设计方法及其应用,并假定读 者已具有多元线性回归分析的基础知识。为了符号上的统 一 ,在12.1.2中列出了回归分析中的主要公式
12.1 回归设计的基本概念 回归设计(也称为响应曲面设计) 目的是寻找试验指标与各因子间的定量规律, 考察的因子都是定量的 。 它是在多元线性回归的基础上用主动收集数据的方法获 得具有较好性质的回归方程的一种试验设计方法。 本章主要介绍Box的回归设计方法及其应用,并假定读 者已具有多元线性回归分析的基础知识。为了符号上的统 一 ,在12.1.2中列出了回归分析中的主要公式

12.1.1 多项式回归模型 在一些试验中希望建立指标y与各定量因子 (又称变量)间相关关系的定量表达式,即回归方程, 以便通过该回归方程找出使指标满足要求的各因子的范 围 。 可以假定 y与 间有如下关系: 这里 是 的一个函数,常称为响应函 数,其图形也称为响应曲面; 是随机误差,通常假定它服从均值为0,方差为 的 正态分布。 在上述假定下, 可以看作为在给定 后 指标的均值,即 p z ,z , ,z 1 2 p z ,z , ,z 1 2 = ( , , , ) + 1 2 p y f z z z ( , , , ) 1 2 p f z z z p z ,z , ,z 1 2 2 ( , , , ) 1 2 p f z z z p z ,z , ,z 1 2 ( ) ( , , , ) 1 2 p E y = f z z z
12.1.1 多项式回归模型 在一些试验中希望建立指标y与各定量因子 (又称变量)间相关关系的定量表达式,即回归方程, 以便通过该回归方程找出使指标满足要求的各因子的范 围 。 可以假定 y与 间有如下关系: 这里 是 的一个函数,常称为响应函 数,其图形也称为响应曲面; 是随机误差,通常假定它服从均值为0,方差为 的 正态分布。 在上述假定下, 可以看作为在给定 后 指标的均值,即 p z ,z , ,z 1 2 p z ,z , ,z 1 2 = ( , , , ) + 1 2 p y f z z z ( , , , ) 1 2 p f z z z p z ,z , ,z 1 2 2 ( , , , ) 1 2 p f z z z p z ,z , ,z 1 2 ( ) ( , , , ) 1 2 p E y = f z z z

称z 的可能取值的空间为因子空间。我们的 任务便是从因子空间中寻找一个点z 0 使E(y) 满足质量要求。 当f的函数形式已知时,可以通过最优化的方法去寻找z 0 。 在许多情况下f的形式并不知道,这时常常用一个多项式去 逼近它,即假定: ( , , , ) 1 2 = p z z z ( , , , ) 0 0 2 0 1 = p z z z (7.1.1) 2 0 = + + + + + i j i j i j j j j j j j j y z z z z 这里各 为未知参数,也称为回归系数,通 常需要通过收集到的数据对它们进行估计。 若用 表示相应的估计,则称 0 , j , jj , ij , b0 ,bj ,bjj ,bij , y b b z b z b z z j j j jj j j ij i j i j = + + + + 0 2 为y关于 z1 ,z2 , ,z p 的多项式回归方程
称z 的可能取值的空间为因子空间。我们的 任务便是从因子空间中寻找一个点z 0 使E(y) 满足质量要求。 当f的函数形式已知时,可以通过最优化的方法去寻找z 0 。 在许多情况下f的形式并不知道,这时常常用一个多项式去 逼近它,即假定: ( , , , ) 1 2 = p z z z ( , , , ) 0 0 2 0 1 = p z z z (7.1.1) 2 0 = + + + + + i j i j i j j j j j j j j y z z z z 这里各 为未知参数,也称为回归系数,通 常需要通过收集到的数据对它们进行估计。 若用 表示相应的估计,则称 0 , j , jj , ij , b0 ,bj ,bjj ,bij , y b b z b z b z z j j j jj j j ij i j i j = + + + + 0 2 为y关于 z1 ,z2 , ,z p 的多项式回归方程

在实际中常用的是如下的一次与二次回归方程(也称一阶 与二阶模型): = + j j j y b b z 0 ˆ ˆ 2 0 = + + + i j i j i j j j j j j j j y b b z b z b z z 一般p个自变量的d次回归方程的系数个数为 + d p d
在实际中常用的是如下的一次与二次回归方程(也称一阶 与二阶模型): = + j j j y b b z 0 ˆ ˆ 2 0 = + + + i j i j i j j j j j j j j y b b z b z b z z 一般p个自变量的d次回归方程的系数个数为 + d p d

12.1.2 多元线性回归 (12.1.1)是一个多项式回归模型,在对变量作了变换并重新 命名后也可以看成是一个多元线性回归模型。 1.回归模型 设所收集到的n组数据为 假定回归模型为: (xi1 , xi2 , , xi p , yi ), i = 1,2, ,n (7.1.5) ~ (0, ) 1,2, , 2 0 1 1 = + + + + = iid N y x x i n i i i p i p i 各 ,
12.1.2 多元线性回归 (12.1.1)是一个多项式回归模型,在对变量作了变换并重新 命名后也可以看成是一个多元线性回归模型。 1.回归模型 设所收集到的n组数据为 假定回归模型为: (xi1 , xi2 , , xi p , yi ), i = 1,2, ,n (7.1.5) ~ (0, ) 1,2, , 2 0 1 1 = + + + + = iid N y x x i n i i i p i p i 各 ,
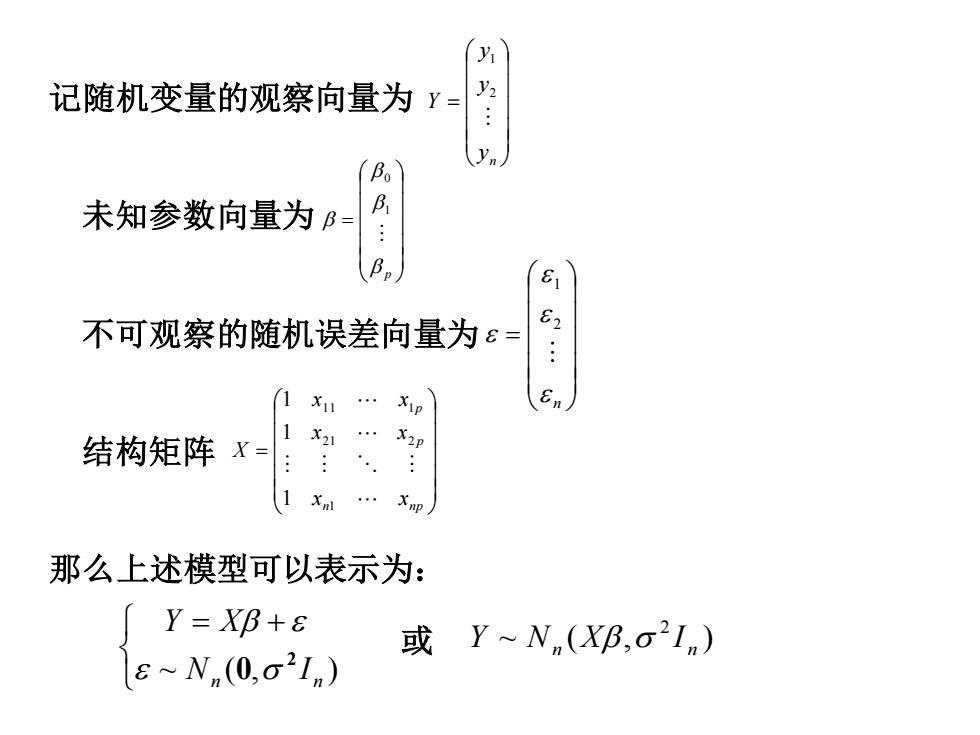
记随机变量的观察向量为 未知参数向量为 不可观察的随机误差向量为 结构矩阵 那么上述模型可以表示为: = n y y y Y 2 1 = p 1 0 = n 2 1 = n np p p x x x x x x X 1 21 2 11 1 1 1 1 = + ~ ( , ) n n N I Y X 2 0 或 ~ ( , ) 2 n n Y N X I
记随机变量的观察向量为 未知参数向量为 不可观察的随机误差向量为 结构矩阵 那么上述模型可以表示为: = n y y y Y 2 1 = p 1 0 = n 2 1 = n np p p x x x x x x X 1 21 2 11 1 1 1 1 = + ~ ( , ) n n N I Y X 2 0 或 ~ ( , ) 2 n n Y N X I

2.回归系数的最小二乘估计 估计回归模型中回归系数的方法是最小二乘法。 记回归系数的最小二乘估计(LSE)为 , 应满足如下正规方程组: 当 存在时,最小二乘估计为 在求得了最小二乘估计后,可以写出回归方程: 今后称 为正规方程组的系数矩阵, 为正规 方程组的常数项向量, 为相关矩阵。 在模型(12.1.5)下,有 ( , , , ) 0 1 = b b b bp XXb = XY ( ) −1 X X b = (X X ) X Y −1 p p y = b + b x ++ b x 0 1 1 ˆ A = X X B = X Y ( ) −1 C = X X ~ ( , ( ) ) 2 −1 b N XX
2.回归系数的最小二乘估计 估计回归模型中回归系数的方法是最小二乘法。 记回归系数的最小二乘估计(LSE)为 , 应满足如下正规方程组: 当 存在时,最小二乘估计为 在求得了最小二乘估计后,可以写出回归方程: 今后称 为正规方程组的系数矩阵, 为正规 方程组的常数项向量, 为相关矩阵。 在模型(12.1.5)下,有 ( , , , ) 0 1 = b b b bp XXb = XY ( ) −1 X X b = (X X ) X Y −1 p p y = b + b x ++ b x 0 1 1 ˆ A = X X B = X Y ( ) −1 C = X X ~ ( , ( ) ) 2 −1 b N XX

若记 C = (X X ) −1 = (cij) ,那么 bj ~ N( j ,cjj ), j 0,1,2, , p 2 = 在通常的回归分析中,由于C非对角阵,所以各回归系数间 是相关的: 2 Cov(bi ,bj ) = cij
若记 C = (X X ) −1 = (cij) ,那么 bj ~ N( j ,cjj ), j 0,1,2, , p 2 = 在通常的回归分析中,由于C非对角阵,所以各回归系数间 是相关的: 2 Cov(bi ,bj ) = cij

3.对回归方程的显著性检验 对回归方程的显著性检验是指检验如下假设: H0: H1: 不全为0 检验方法是作方差分析。 记 则有平方和分解式 其中 为残差平方和,自由度为 为回归平方和,自由度为 当H0为真时,有 对于给定的显著性水平 ,拒绝域为 。 1 = 2 = = p = 0 p , , , 1 2 y ˆ i = b0 + b1 xi1 ++ bp xi p,i = 1,2, ,n E R n i i n i i i n i ST = yi − y = y − y + y − y = S + S = = =1 2 1 2 1 2 ( ) ( ˆ ) ( ˆ ) = − i E i i S y y 2 ( ˆ ) f E = n − p −1 = − 2 S (y ˆ y) R i f R = p ~ ( , ) ( , 1) / / = F f f = F p n − p − S f S f F R E E E R R ( , 1) F F1− p n − p −
3.对回归方程的显著性检验 对回归方程的显著性检验是指检验如下假设: H0: H1: 不全为0 检验方法是作方差分析。 记 则有平方和分解式 其中 为残差平方和,自由度为 为回归平方和,自由度为 当H0为真时,有 对于给定的显著性水平 ,拒绝域为 。 1 = 2 = = p = 0 p , , , 1 2 y ˆ i = b0 + b1 xi1 ++ bp xi p,i = 1,2, ,n E R n i i n i i i n i ST = yi − y = y − y + y − y = S + S = = =1 2 1 2 1 2 ( ) ( ˆ ) ( ˆ ) = − i E i i S y y 2 ( ˆ ) f E = n − p −1 = − 2 S (y ˆ y) R i f R = p ~ ( , ) ( , 1) / / = F f f = F p n − p − S f S f F R E E E R R ( , 1) F F1− p n − p −