
第11章 统计综合评价 学习目标 1、了解综合评价的基本概念、特点及一般程序: 2、学握选择评价指标的几种主要方法: 3、掌握对评价指标进行无量纲处理的几种主要方法 4、徵握平价指标权重的集中计算方法 5、掌握评价项目的几种综合方法。 基本概念 综合评价评价指标体系聚类分析法主成分分析法层次分析法总分评定法 加权平均法距离综合法 11.1统计综合评价概述 11.1.1统计综合评价的概念 统计综合评价简称综合评价就是根据统计分析研究的目的,依据己有的统计资料,借助 统计理论和方法,对研究对象及其组成部分的数量规模大小、水平高低、速度快慢、质量状 况及内部协调状况做出定量的判断,得出概括性的结论,从而揭示事物的本质及其发展规律 的一种统计分析方法。 构成统计综合平价的基本要素有被平价对象、评价指标体系、评价指标的权重系数、筑 合评价模型、评价主 评价原则、 评价环境等有机组合构 一个综合评价系统 综合评价跟单项指标的区别在于,单项指标是利用一个统计指标对事物的某一方面作出 判断:而综合评价则是对被研究的现象总体,通过建立一个统计指标体系,对客观事物进行 多方面或多层次的分析研究,以揭示事物的本质和规律。 综合评价是统计工作的一个重要内容,试统计活动讨程而言,统计综合评价是缘统计调 查、统计整理之后的一项重要的工作,是体现统计职能、发挥统计作用 、实现统计价值的关 键环节。综合评价是统计决策基础,客观科学的评价事物,是正确决策的指导。 11.1.2综合评价的特点 统计综合评价具有以下特点: 一,综合评价包括多个评价指标,并由此构成一个评价指标体系 第 ,综合评价中的多个评价指标是分别描述评价对象系统的各个方面,它们应该包含 被评价对象系统的全部信息 第三,各个评价指标在整个评价指标体系中的重要性是不一样的,因此各个评价指标的 权重也应该有所不同。 第四,各个评价指标的具体最纲是各不相同的,不同量纲的指标值之间无法进行相互比 较,综合评价的前提是必须把不同量纲的 标值转化为无量纲的相 对评价值 第五,依据评价对象系统的属性特点来选择不同的评价方法,建立相应的综合评价模型 把各指标评估值合成在一起,计算出综合评价结果,对评价对象系统进行比较分析,得出一 个整体性的评价
1 第 11 章 统计综合评价 学习目标 1、了解综合评价的基本概念、特点及一般程序; 2、掌握选择评价指标的几种主要方法; 3、掌握对评价指标进行无量纲处理的几种主要方法; 4、掌握评价指标权重的集中计算方法; 5、掌握评价项目的几种综合方法。 基本概念 综合评价 评价指标体系 聚类分析法 主成分分析法 层次分析法 总分评定法 加权平均法 距离综合法 11.1 统计综合评价概述 11.1.1 统计综合评价的概念 统计综合评价简称综合评价就是根据统计分析研究的目的,依据已有的统计资料,借助 统计理论和方法,对研究对象及其组成部分的数量规模大小、水平高低、速度快慢、质量状 况及内部协调状况做出定量的判断,得出概括性的结论,从而揭示事物的本质及其发展规律 的一种统计分析方法。 构成统计综合评价的基本要素有被评价对象、评价指标体系、评价指标的权重系数、综 合评价模型、评价主体、评价原则、评价环境等有机组合构成一个综合评价系统。 综合评价跟单项指标的区别在于, 单项指标是利用一个统计指标对事物的某一方面作出 判断;而综合评价则是对被研究的现象总体,通过建立一个统计指标体系,对客观事物进行 多方面或多层次的分析研究,以揭示事物的本质和规律。 综合评价是统计工作的一个重要内容,就统计活动过程而言,统计综合评价是继统计调 查、统计整理之后的一项重要的工作,是体现统计职能、发挥统计作用、实现统计价值的关 键环节。综合评价是统计决策基础,客观科学的评价事物,是正确决策的指导。 11.1.2 综合评价的特点 统计综合评价具有以下特点: 第一,综合评价包括多个评价指标,并由此构成一个评价指标体系; 第二,综合评价中的多个评价指标是分别描述评价对象系统的各个方面,它们应该包含 被评价对象系统的全部信息; 第三,各个评价指标在整个评价指标体系中的重要性是不一样的, 因此各个评价指标的 权重也应该有所不同。 第四,各个评价指标的具体量纲是各不相同的,不同量纲的指标值之间无法进行相互比 较,综合评价的前提是必须把不同量纲的指标值转化为无量纲的相对评价值; 第五, 依据评价对象系统的属性特点来选择不同的评价方法, 建立相应的综合评价模型, 把各指标评估值合成在一起,计算出综合评价结果,对评价对象系统进行比较分析,得出一 个整体性的评价

11.1.3统计综合评价的一般程序 1,明确评价对象系统和评价目的 行综合评价, 首先必须明确评价谁,即明确综合评价的对象系统。它可以是自然 界的对象系统,也可以是技术对象系统、 人工制造的对象系统或社会经济的对象系统等等 如对某一区域的国民经济发展的评价。其次,对于平价的对象系统在开始具体评价之前,还 必须确定评价的目的,即评价的结果是干什么用的。不同的综合评价目的,所选用的指标体 系也就有所不同,只有日标明确,才有针对性。这是一项基础性的工作, 2.对评价对象系统进行系统分析,明确评价对象系统的主要属性 建立评价指标体系的前提是必须对评价对象系统进行系统分析。要运用系统论的观点 和系统分析方法,通过对评价对象系统的系统分析,搞清楚评价对象系统所包括的范围、构 成要素、数量特征和数量表现等内容,对评价对象系统的现象和本质进行研究,从而明确评 价对象系统的主要屈性,进而为选取评价指标建立评价指标体系奠定良好基础。 3.选取评价指标,构建评价指标体系 选取评价指标 构建评价 标体系是整个综合评价工作的关键 百分 必须明确选取评 价指标的指导思想和应遵循的基本原则:在此基础上,根据评价的目的及其主要属性,将词 价对象系统分解成不同的分目标:然后采用定性分析与定量分析相结合的方法选择合适的 评价指标,最终建立一个能够从不同角度,不同侧面反映评价对象本质特征的评价指标体系。 新物建综合平价指标体系 一定要考虑现象之间的相互联系,即质上联系的逻辑性和量上的度 量性 其联系可以是单一层次的,也可以是多层次的 4.确定各评价指标的权重 评价指标的权重是指各个评价指标在整个评价指标体系中相对重要性的数量表现。 般来说,评价对象系统的各个评价指标在整个评价指标体系中的作用是不一样的,因此各个 评价指标的权重也应该有所不同。尽管权数的表现形式多种多样,但就其主要功能和作用来 说,权数始终起若权衡轻重的作用。 如何根据评 对象系统的特点 科学合理地确定各个评价指标在整个评价指标体系中 的作用对评价结果的合理与否有者至关重要的影响。 确定评价指标权重的方法有主观赋权法和客观武权法两类。 5.对评价指标进行无量纲化处理 综合评价需要运用由多个评价指标组成的评价指标体系,而这些评价指标分别反映评价 对象系统的不同侧面 般具有不同的性质,且计量单位往往也不 样, 因而必须解决不 指标的同度量问题,即对其进行无量纲化处理,消除指标量纲的影响,使不同评价指标之间 具有可比性,以便对评价对象系统作出综合评价。 无量纲化处理即对评价指标数值进行标准化、正规化处理。它是通过一定的数学变换来 消除原始指标量纲影响的方法,即把性质、量纲各异的评价指标值转化为能够进行相互比 较的相对数,即评价值 6.选择评价方法,建立综合评价模型,计算综合评价结果 指标权重的确定和指标值的无量纲处理是计算综合评价结果的准备,在经过上述各项 作之后,还必须选择评价方法,建立一个综合评价模型,将各个自系统有机组合起来,从总 体角度对评价对象系统进行定量分析和综合评价。 综合评价的方法很多, 可以根据评价对象系统的属性特点来选择不同的方法,建立相应 的评价模型,如线性加权和函数 成分 模 评价等 选择不同的方法建立相应的综合评价模型,将指标值或无量纲化处理后的量化值代入相 应的模型,即可得出综合评价结果。 7,根据综合评价结果进行统计分析
2 11.1.3 统计综合评价的一般程序 1.明确评价对象系统和评价目的 要进行综合评价,首先必须明确评价谁,即明确综合评价的对象系统。它可以是自然 界的对象系统,也可以是技术对象系统、人工制造的对象系统或社会经济的对象系统等等, 如对某一区域的国民经济发展的评价。其次,对于评价的对象系统在开始具体评价之前,还 必须确定评价的目的,即评价的结果是干什么用的。不同的综合评价目的,所选用的指标体 系也就有所不同,只有目标明确,才有针对性。这是一项基础性的工作。 2.对评价对象系统进行系统分析,明确评价对象系统的主要属性 建立评价指标体系的前提是必须对评价对象系统进行系统分析。要运用系统论的观点 和系统分析方法,通过对评价对象系统的系统分析,搞清楚评价对象系统所包括的范围、构 成要素、数量特征和数量表现等内容,对评价对象系统的现象和本质进行研究,从而明确评 价对象系统的主要属性,进而为选取评价指标建立评价指标体系奠定良好基础。 3.选取评价指标,构建评价指标体系 选取评价指标,构建评价指标体系是整个综合评价工作的关键。首先必须明确选取评 价指标的指导思想和应遵循的基本原则;在此基础上,根据评价的目的及其主要属性,将评 价对象系统分解成不同的分目标;然后采用定性分析与定量分析 相结合的方法选择合适的 评价指标, 最终建立一个能够从不同角度, 不同侧面反映评价对象本质特征的评价指标体系。 所构建综合评价指标体系一定要考虑现象之间的相互联系, 即质上联系的逻辑性和量上的度 量性。其联系可以是单一层次的,也可以是多层次的。 4.确定各评价指标的权重 评价指标的权重是指各个评价指标在整个评价指标体系中相对重要性的数量表现。一 般来说,评价对象系统的各个评价指标在整个评价指标体系中的作用是不一样的,因此各个 评价指标的权重也应该有所不同。尽管权数的表现形式多种多样, 但就其主要功能和作用来 说,权数始终起着权衡轻重的作用。 如何根据评价对象系统的特点,科学合理地确定各个评价指标在整个评价指标体系中 的作用对评价结果的合理与否有着至关重要的影响。 确定评价指标权重的方法有主观赋权法和客观赋权法两类。 5.对评价指标进行无量纲化处理 综合评价需要运用由多个评价指标组成的评价指标体系, 而这些评价指标分别反映评价 对象系统的不同侧面,一般具有不同的性质,且计量单位往往也不一样,因而必须解决不同 指标的同度量问题,即对其进行无量纲化处理,消除指标量纲的影响,使不同评价指标之间 具有可比性,以便对评价对象系统作出综合评价。 无量纲化处理即对评价指标数值进行标准化、正规化处理。它是通过一定的数学变换来 消除原始指标量纲影响的方法,即把性质 、量纲各异的评价指标值转化为能够进行相互比 较的相对数,即评价值。 6.选择评价方法,建立综合评价模型,计算综合评价结果 指标权重的确定和指标值的无量纲处理是计算综合评价结果的准备, 在经过上述各项工 作之后,还必须选择评价方法,建立一个综合评价模型,将各个自系统有机组合起来,从总 体角度对评价对象系统进行定量分析和综合评价。 综合评价的方法很多, 可以根据评价对象系统的属性特点来选择不同的方法,建立相应 的评价模型,如线性加权和函数、主成分分析法即模糊综合评价等。 选择不同的方法建立相应的综合评价模型, 将指标值或无量纲化处理后的量化值代入相 应的模型,即可得出综合评价结果。 7.根据综合评价结果进行统计分析

综合评价结果是一个综合性的指数体系,按评价指标体系的层次结构划分有总目标指 数、子目标指以及子子目标指数等等,依据各个指数的计算结果即可讲行综合评价结果的 分析。被评价对象系统的综合评价结果指数就是评价目的所要掌据的评价对象所处的实际水 比较分析各个评价对象彼此之间各项准则或子目标的评价结果指数可以找出各自的 势、劣势、差距和不足。 8.作出综合评价的结论 根据综合评价结果,作出综合评价的结论,即明确评价对象在评价目的发的排列顺序或 有关目标的差距,病根据统计分析的结果,找出评价对象系统中目前存在的问题和薄弱环节, 分析问题产生的原因 进而有针对性地提出相应的扬长避短的对策措 11.2.4综合评价的局限性 1.综合评价结果具有相对性 综合评价结果尽管采用了一定的数学模型,其结果用数值来表达,但一般不具有统计指 标的独立意义,而只有相对意义,即只能用于性质相同的对象之间的比较和排序 2.综合评价的结果不具有唯 性 综合评价可采用的方法很多,选择不同的评价方法,可能有不同的结果。即使采用同 种方法,也会由于诸如评语等级的拟定、各等级所赋予的分值的拟定、单因素评价方法的评 定、评价的相对标准的拟定、单因素平价结果的合成等环节上的不同而出现不同的端合评价 结果 3.综合评价结果常带有主观性 在综合评价中,各指标的评价标准以及权数的确定,常常需要依靠有关专家来确定,不 同的专家给出的标准和权重会有所差异,因此,综合评价的结果,往往带来一定的主观性。 4,综合评价结果的可比性存在一定的局限 如前所述,评价对象的比较和排序只能在同一参照系内讲行,评价的结论也只有在同 参照系内才有可比性 那些非数量评判因素进行评判时 般要请 一些专家对评判进行 等级评定及投票。不同的转家进行评判所依据的标准不尽相同,因而,据此得出的不同对象 的评判结果一般不具有可比性。可见,综合评价结果的可比性在范围上有较大的局限性。 由于综合评价分析方法的局限性,使它她的结论只能作为认识事物、分析问题的参考。 而不能作为决策的唯一依据。 11.2综合评价过程 11.2.1评价指标的确定 1.评价指标的选择原则 对客观现象进行统计综合评价,关键是要科学地选择评价项目,建立一个合适的评价指 标体系。选择评价指标体系应遵循如下原则: )目的性原则。评价指标体系的设计要切题,所选择的评价指标应与研究目的相吻合 (2)客观性原则。评价指标体系能正确地把握所要研究问题的本质和内函,能够客观地 反映事物的主要特征。 (3)全面性原则。评价指标体系中的各个评价指标应能从不同的角度综合反映评价对象 系统的全貌 (④敏感性原则。所选择的评价指标应能比较敏感地反映评价对象系统的变化 (⑤)相互独立性原则。尽可能选择相关程度低的指标,各个评价指标之间的关系应该是 互斥与互补的有机统一。 (6)可比性原则。评价指标含义明确,计算口径一致,达到动态可比、横向可比 3
3 综合评价结果是一个综合性的指数体系,按评价指标体系的层次结构划分有总目标指 数、子目标指数以及子子目标指数等等,依据各个指数的计算结果即可进行综合评价结果的 分析。 被评价对象系统的综合评价结果指数就是评价目的所要掌握的评价对象所处的实际水 平,比较分析各个评价对象彼此之间各项准则或子目标的评价结果指数可以找出各自的优 势、劣势、差距和不足。 8.作出综合评价的结论 根据综合评价结果,作出综合评价的结论, 即明确评价对象在评价目的发的排列顺序或 有关目标的差距, 病根据统计分析的结果, 找出评价对象系统中目前存在的问题和薄弱环节, 分析问题产生的原因,进而有针对性地提出相应的扬长避短的对策措施。 11.2.4 综合评价的局限性 1.综合评价结果具有相对性 综合评价结果尽管采用了一定的数学模型,其结果用数值来表达, 但一般不具有统计指 标的独立意义,而只有相对意义,即只能用于性质相同的对象之间的比较和排序。 2.综合评价的结果不具有唯一性 综合评价可采用的方法很多,选择不同的评价方法,可能有不同的结果。即使采用同一 种方法,也会由于诸如评语等级的拟定、各等级所赋予的分值的拟定、单因素评价方法的评 定、评价的相对标准的拟定、单因素评价结果的合成等环节上的不同而出现不同的综合评价 结果。 3.综合评价结果常带有主观性 在综合评价中,各指标的评价标准以及权数的确定,常常需要依靠有关专家来确定,不 同的专家给出的标准和权重会有所差异,因此,综合评价的结果,往往带来一定的主观性。 4.综合评价结果的可比性存在一定的局限 如前所述,评价对象的比较和排序只能在同一参照系内进行,评价的结论也只有在同 一参照系内才有可比性。对那些非数量评判因素进行评判时,一般要请一些专家对评判进行 等级评定及投票。不同的专家进行评判所依据的标准不尽相同,因而,据此得出的不同对象 的评判结果一般不具有可比性。可见,综合评价结果的可比性在范围上有较大的局限性。 由于综合评价分析方法的局限性,使它她的结论只能作为认识事物、分析问题的参考。 而不能作为决策的唯一依据。 11.2 综合评价过程 11.2.1 评价指标的确定 1.评价指标的选择原则 对客观现象进行统计综合评价, 关键是要科学地选择评价项目,建立一个合适的评价指 标体系。选择评价指标体系应遵循如下原则: (1) 目的性原则。 评价指标体系的设计要切题, 所选择的评价指标应与研究目的相吻合。 (2) 客观性原则。评价指标体系能正确地把握所要研究问题的本质和内涵, 能够客观地 反映事物的主要特征。 (3) 全面性原则。 评价指标体系中的各个评价指标应能从不同的角度综合反映评价对象 系统的全貌。 (4) 敏感性原则。所选择的评价指标应能比较敏感地反映评价对象系统的变化。 (5) 相互独立性原则。 尽可能选择相关程度低的指标,各个评价指标之间的关系应该是 互斥与互补的有机统一。 (6) 可比性原则。评价指标含义明确,计算口径一致,达到动态可比、横向可比

(⑦)可操作性原则。评价指标体系要考虑资料收集的可能性,尽可能地利用现有的统计 资料 2评价指标的选择方法 选择评价指标的方法有两种:即定性方法和定量方法。 (1)定性方法 常用的定性方法有:综合法和分析法。 综合法一般是指通过研讨会或征询专家意见的方式,集中专家们的意见,以确定评价指 标。这种方法是借助专家的智力优势和经验以选择评价指标的。根据专家意见的集中和分散 情况,可以采取一次或多次的形式选择确定。当选择指标的意见分散时,还要进行客观分析, 在准确分析问题的基础上,改进征询意见的组织方式,以获得理想的指标选择效果。 分析法是将评价的对象划分为若干各组成部分或不同的侧面,明确各个部分或侧面所要 评价问题的内涵和外延,在此基础上,对每一侧面分别选用一个或着干个指标以反映评价对 象的特征。如何把握各个部分或各个侧面的重点指标是运用分析法的关键。这种方法的运用 与人们的工作经验和求真务实的科学态度密切相关。 (2)定量方法 常用的定量方法有:试算法、聚类分析法和主成分分析法等几种。 第一种方法:试算法是通过历史资料的试算来判断指标的有效性。例如,要评价全国名 地区2005年可持续发展战略的实施绩效,可以2003年和2004年的数据进行试算,通过试 算结果判断所选 省标的合适性 然后对相关指标进行科学 比较,把那些代表性强的指标纳 指标体系的构建之中,然后反复修正指标体系直至满意为止。 第二种方法:聚类分析法 聚类分析在选择指标方面的基本思路是:如果有若干个指标,首先将每一个指标看成 类,然后根据指标间的相似程度,通过比较类间臣离进行并类。每次将距离最近的两类加以 合并金下N1举。再洗择这N-1举中距离最斤的两类加1合并。金下-》米。依次举推 ,每合并 继续这 过程,直至将所有指标合并成为 类为止, 形成 由小到大的分类系统,即暗系。最后整个分类结果画在一张图上,称为聚类图或谱系图,以 此直观地反映各指标间的亲疏关系。聚类分析法的具体实施步骤: ①选择度量指标间相似程度的方法。常用的方法是相关系数法。各指标两两之间都可以 计算相关系数,从而形成一个相关系数矩阵。 ②选择度量指标类间距离的方法。常用的方法有最长距离法 最短距离法、重心法、类 平均法、离差平方和法。由于一般利用相关系数表示指标(类)间的相似程度,所以多采用 相关系数量大法进行聚类。 ③根据聚类结果绘制聚类图。根据聚类结果确定指标体系,必须以相关程度作为划分标 准。至于分类时用的阀值为多少,要视对指标的简约性要求不同而定。若对指标体系的简约 性要求不高,可选择较高的相关系数作为 ,反之亦然 ④根据最后划分的类别确定指标体系。由于同一类中指标的相似程度相高,即信息重复 较多,可以选择其中之一作为代表,从而达到简化指标的目的。 [例11-1]假定我们初步选择了某事物各个不同侧面特征的指标共8个,记为 X,X,·.X。已知各指标之间的相关系数矩阵见表11-1 表11-1指标相关系数矩阵 X X X.X X。 X
4 (7) 可操作性原则。评价指标体系要考虑资料收集的可能性,尽可能地利用现有的统计 资料。 2.评价指标的选择方法 选择评价指标的方法有两种:即定性方法和定量方法。 (1)定性方法 常用的定性方法有:综合法和分析法。 综合法一般是指通过研讨会或征询专家意见的方式, 集中专家们的意见,以确定评价指 标。这种方法是借助专家的智力优势和经验以选择评价指标的。根据专家意见的集中和分散 情况, 可以采取一次或多次的形式选择确定。 当选择指标的意见分散时, 还要进行客观分析, 在准确分析问题的基础上,改进征询意见的组织方式,以获得理想的指标选择效果。 分析法是将评价的对象划分为若干各组成部分或不同的侧面, 明确各个部分或侧面所要 评价问题的内涵和外延,在此基础上,对每一侧面分别选用一个或若干个指标以反映评价对 象的特征。如何把握各个部分或各个侧面的重点指标是运用分析法的关键。 这种方法的运用 与人们的工作经验和求真务实的科学态度密切相关。 (2)定量方法 常用的定量方法有:试算法、聚类分析法和主成分分析法等几种。 第一种方法:试算法是通过历史资料的试算来判断指标的有效性。例如,要评价全国各 地区 2005 年可持续发展战略的实施绩效,可以 2003 年和 2004 年的数据进行试算,通过试 算结果判断所选指标的合适性, 然后对相关指标进行科学比较,把那些代表性强的指标纳入 指标体系的构建之中,然后反复修正指标体系直至满意为止。 第二种方法:聚类分析法 聚类分析在选择指标方面的基本思路是: 如果有若干个指标,首先将每一个指标看成一 类,然后根据指标间的相似程度,通过比较类间距离进行并类。每次将距离最近的两类加以 合并,余下 N-1 类。再选择这 N-1 类中距离最近的两类加以合并,余下 N-2 类。依次类推。 这样,每合并一次,就减少一类,继续这一过程,直至将所有指标合并成为一类为止,形成 由小到大的分类系统,即谱系。最后整个分类结果画在一张图上,称为聚类图或谱系图,以 此直观地反映各指标间的亲疏关系。聚类分析法的具体实施步骤: ①选择度量指标间相似程度的方法。常用的方法是相关系数法。各指标两两之间都可以 计算相关系数,从而形成一个相关系数矩阵。 ②选择度量指标类间距离的方法。常用的方法有最长距离法、最短距离法、重心法、类 平均法、离差平方和法。由于一般利用相关系数表示指标(类)间的相似程度,所以多采用 相关系数量大法进行聚类。 ③根据聚类结果绘制聚类图。根据聚类结果确定指标体系,必须以相关程度作为划分标 准。至于分类时用的阈值为多少,要视对指标的简约性要求不同而定。若对指标体系的简约 性要求不高,可选择较高的相关系数作为阈值,反之亦然。 ④根据最后划分的类别确定指标体系。由于同一类中指标的相似程度相高, 即信息重复 较多,可以选择其中之一作为代表,从而达到简化指标的目的。 [例 11-1]假定我们初步选择了某事物各个不同侧面特征的指标共 8 个,记为 1 2 8 X X L , X 。已知各指标之间的相关系数矩阵见表 11-1。 表 11-1 指标相关系数矩阵 X1 X2 X3 X4 X5 X6 X7 X8
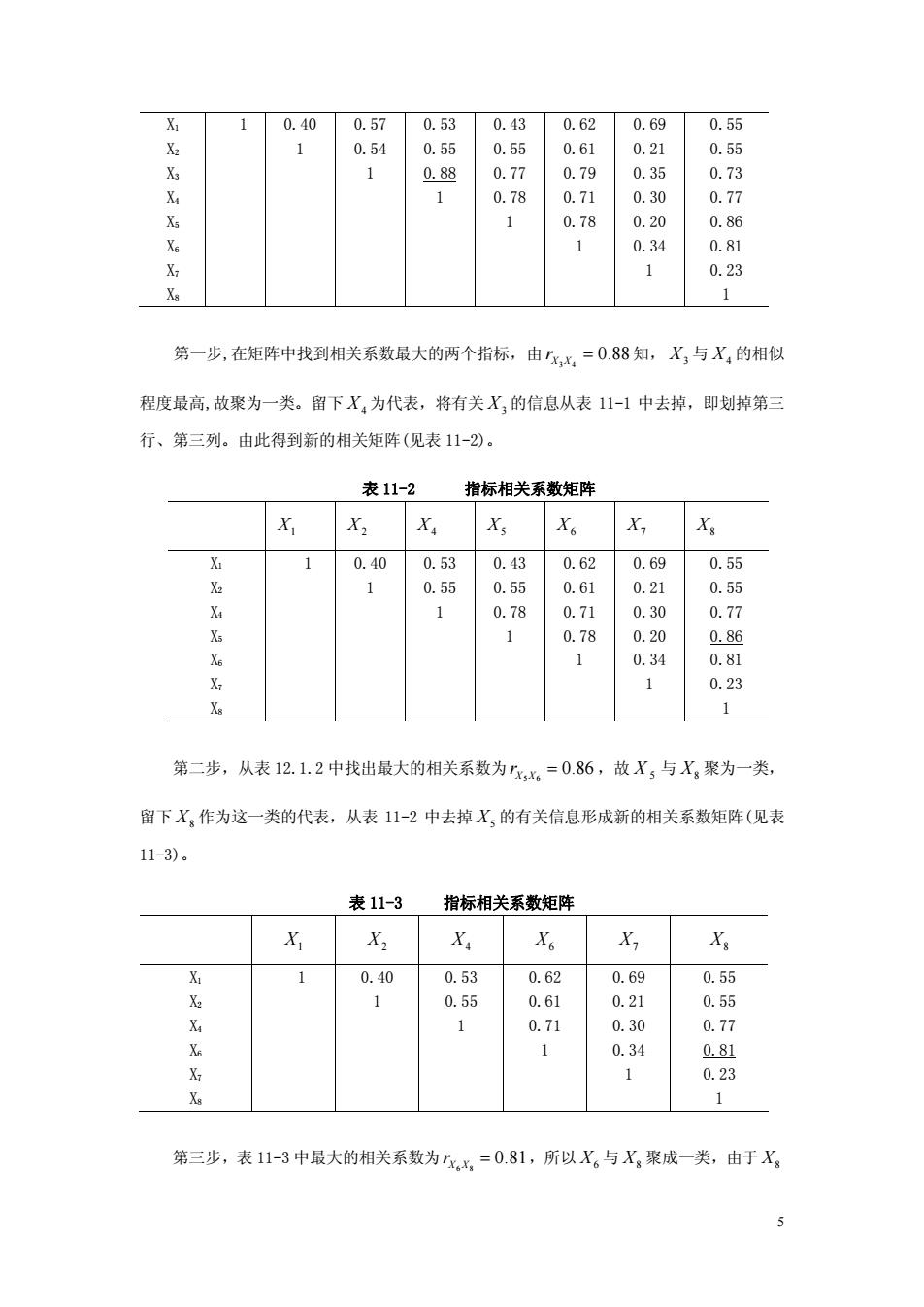
1 0.40 0.57 0.53 0.43 0.62 0.69 0.55 1 0.54 0.55 0.55 0.61 0.2 0.55 1 86 1 0.78 0.20 0.86 0.34 0.81 X 1 0.23 第一步,在矩阵中找到相关系数最大的两个指标,由x,X=0.88知,X,与X,的相似 程度最高,故聚为一类。留下X,为代表,将有关X的信息从表11-1中去掉,即划掉第三 行、第三列。由此得到新的相关矩阵(见表11-2)。 表11-2 指标相关系数矩阵 X X X; Xo X, X. 1 0.40 0.53 0.43 0.62 0.69 0.55 1 0.55 0.55 0.61 0.2 0.55 1 0.78 0.71 0.30 0.77 1 0.78 0.20 0.34 &8 1 0.23 第二步,从表12.1.2中找出最大的相关系数为5,=0.86,故X,与X聚为一类, 留下X,作为这一类的代表, 从表11-2中去掉X,的有关信息形成新的相关系数矩阵(见表 11-3). 表11-3 指标相关系数矩阵 X X X X。 X, X X 0.40 0.53 0.62 0.69 0.55 0.55 0.61 0.21 0.55 0.7 0.30 0.34 0.23 1 第三步,表11-3中最大的相关系数为r,x=0.81,所以X。与X,聚成一类,由于X。 5
5 X1 X2 X3 X4 X5 X6 X7 X8 1 0.40 1 0.57 0.54 1 0.53 0.55 0.88 1 0.43 0.55 0.77 0.78 1 0.62 0.61 0.79 0.71 0.78 1 0.69 0.21 0.35 0.30 0.20 0.34 1 0.55 0.55 0.73 0.77 0.86 0.81 0.23 1 第一步,在矩阵中找到相关系数最大的两个指标,由 3 4 0.88 X X r = 知, X3 与 X4 的相似 程度最高,故聚为一类。留下 X4 为代表,将有关 X3 的信息从表 11-1 中去掉,即划掉第三 行、第三列。由此得到新的相关矩阵(见表 11-2)。 表 11-2 指标相关系数矩阵 X1 X2 X4 X5 X6 X7 X8 X1 X2 X4 X5 X6 X7 X8 1 0.40 1 0.53 0.55 1 0.43 0.55 0.78 1 0.62 0.61 0.71 0.78 1 0.69 0.21 0.30 0.20 0.34 1 0.55 0.55 0.77 0.86 0.81 0.23 1 第二步,从表 12.1.2 中找出最大的相关系数为 5 6 0.86 X X r = ,故 X 5 与 X8 聚为一类, 留下 X8 作为这一类的代表,从表 11-2 中去掉 X5 的有关信息形成新的相关系数矩阵(见表 11-3)。 表 11-3 指标相关系数矩阵 X1 X2 X4 X6 X7 X8 X1 X2 X4 X6 X7 X8 1 0.40 1 0.53 0.55 1 0.62 0.61 0.71 1 0.69 0.21 0.30 0.34 1 0.55 0.55 0.77 0.81 0.23 1 第三步,表 11-3 中最大的相关系数为 6 8 0.81 X X r = ,所以 X6 与 X8 聚成一类,由于 X8

己与X,聚成一类了,所以该步实际上是将X,X。X,聚为一类。 重复这一过程,直至将所有指标聚为一类为止。由于有8个指标,所以需要七步(第 四步至第七步聚类过程从略)。最终形成聚类图(谱系图)如图1-1所示。 0.5 17234658指标序号 图11-1聚类图(谱系图) 利用聚类图,我们就可以对指标进行精简了,若以r=0.8作为分类的阀值,则8个指 标可分为5类,X、X2、X,、(X、X)(X,、X。、X,如果第四类中选X,为 代表,舍掉X,第五类中选X,为代表,舍掉X,和X,那么最终的指标体系包括五个指 标:X、X2、X,、X,、X,。当然,若对指标体系的简约性要求较高,可以选低一些的 阙值,如选r=0.65,那么8个指标可分为三类即(X,、X,)、X2、(X,、X4、X、 X。、X,),第一类和第三类中各选一个代表指标(至于选哪一个,需要根据指标的性质及 经验决定),而将其它的指标删除,则最终的指标体系将由3个指标构成,这藏达到了我们 简化指标体系的目的。 第三种方法 主成分分析法 主成分分析就是设法将原来众多的具有一定相关性的指标(比如P个指标),重新组合成 一组新的相互无关的综合指标来代替原来的指标。通常数学上的处理就是将原米p个指标作 线性组合,若没有限制条件作为新的综合指标,这样的线性组合会有很多,那么如何去选取呢? 主成分分析的基本思想是:如果将选取的第一个线性组合即第一个综合指标记为下1,自然希 望下1尽可能多的反映原来指标的信息 这里的“信息”最经典的方法就 用F1的方差米 表达,即aFI)越大表示F1包含的信息越多。因此在所有的线性组合中所选取的F1应该 方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考 虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不在需要出现在 F2中用数学语言表达就是要求C。w(F12=0,称F2为第二主成分依次类推可以造出第三 四第。个主成分。不难相这此主成分之间 不仅不相关,而且它们的 差依次递减因此在 实际工作中,就挑选前几个最大主成分虽然这 部分信 抓住了主要 矛盾,并从原始数据中进一步提取了某些新的信息,这种既减少了变量的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。 主成分分析计算步骤如下:
6 已与 X5 聚成一类了,所以该步实际上是将 X5 X6 X8 聚为一类。 重复这一过程,直至将所有指标聚为一类为止。由于有 8 个指标,所以需要七步(第 四步至第七步聚类过程从略)。最终形成聚类图(谱系图)如图 1-1 所示。 0.5 1 7 2 3 4 6 5 8 指标序号 图 11-1 聚类图(谱系图) 利用聚类图,我们就可以对指标进行精简了,若以r = 0.8 作为分类的阈值,则 8 个指 标可分为 5 类, X1 、 X2 、 X7 、( X3 、 X4 )、( X5 、 X6 、 X8 ),如果第四类中选 X4 为 代表,舍掉 X3 ,第五类中选 X5 为代表,舍掉 X6 和 X8 ,那么最终的指标体系包括五个指 标: X1 、 X2 、 X7 、 X3 、 X5 。当然,若对指标体系的简约性要求较高,可以选低一些的 阈值,如选r = 0.65 ,那么 8 个指标可分为三类即( X1 、 X7 )、 X2 、( X3 、 X4 、 X5 、 X6 、 X8 ),第一类和第三类中各选一个代表指标(至于选哪一个,需要根据指标的性质及 经验决定),而将其它的指标删除,则最终的指标体系将由 3 个指标构成,这就达到了我们 简化指标体系的目的。 第三种方法:主成分分析法 主成分分析就是设法将原来众多的具有一定相关性的指标(比如 p 个指标),重新组合成 一组新的相互无关的综合指标来代替原来的指标。 通常数学上的处理就是将原来 p 个指标作 线性组合,若没有限制条件作为新的综合指标,这样的线性组合会有很多,那么如何去选取呢? 主成分分析的基本思想是:如果将选取的第一个线性组合即第一个综合指标记为 F1,自然希 望 F1 尽可能多的反映原来指标的信息。这里的“信息”最经典的方法就是用 F1 的方差来 表达,即 Var(F1)越大,表示 F1 包含的信息越多。 因此在所有的线性组合中所选取的 F1 应该是 方差最大的,故称 F1 为第一主成分。如果第一主成分不足以代表原来 p 个指标的信息,再考 虑选取 F2 即选第二个线性组合,为了有效地反映原来信息,F1 已有的信息就不在需要出现在 F2 中,用数学语言表达就是要求 Cov(F1,F2)=0,称 F2 为第二主成分,依次类推可以造出第三, 第四,第 p 个主成分。 不难想象这些主成分之间不仅不相关,而且它们的方差依次递减,因此在 实际工作中,就挑选前几个最大主成分"虽然这样做会损失一部分信息,但是由于抓住了主要 矛盾,并从原始数据中进一步提取了某些新的信息,这种既减少了变量的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。 主成分分析计算步骤如下:
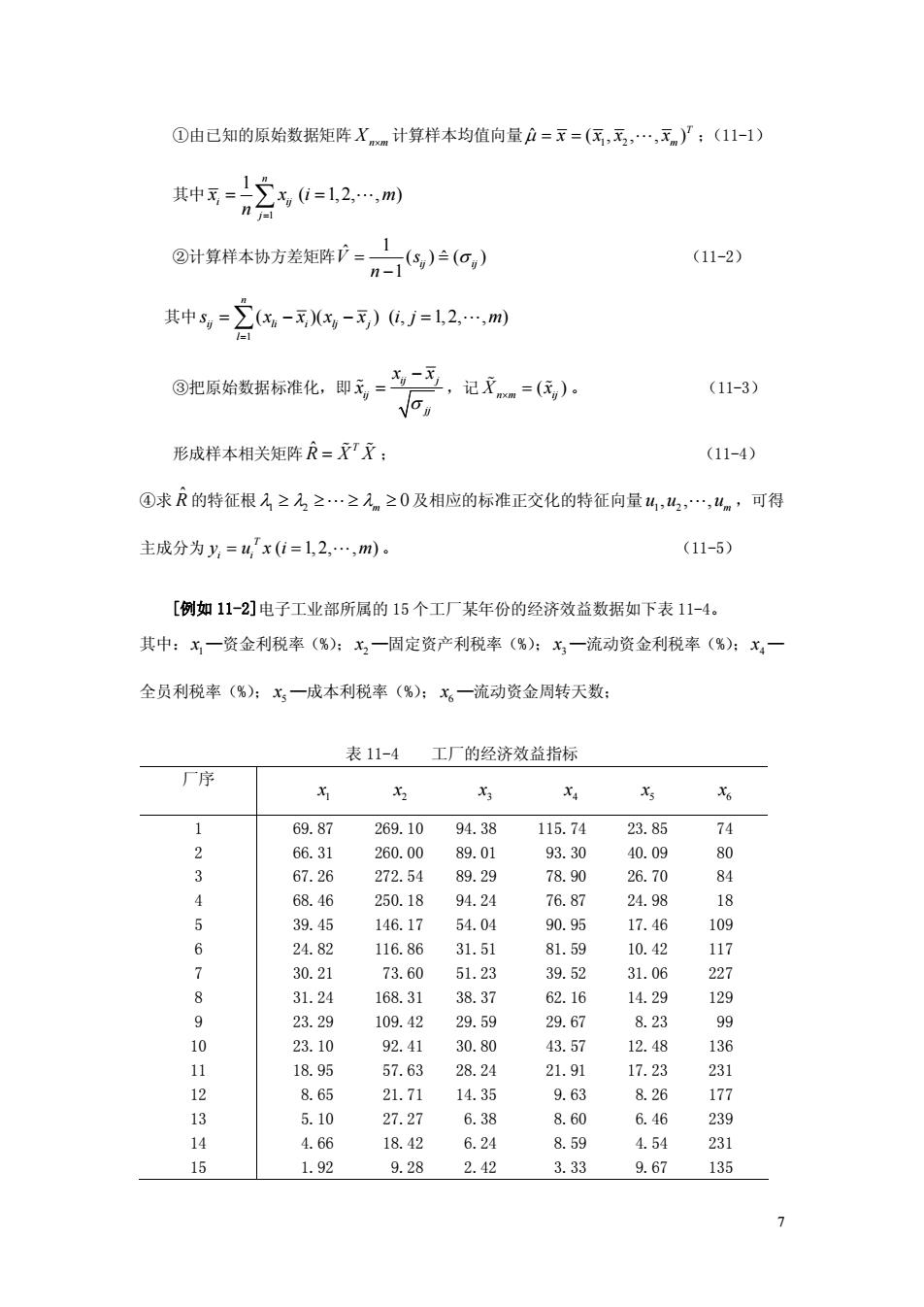
①由己知的原始数据矩阵Xm计算样本均值向量户=x=(民,无,.,x)了;(11-1) 种=2,=12m ②计算样本协方差矩阵严= )(o,) (11-2) 其中号=-,-》j=l2,m) ③把原始数据标准化,即元,-一三,记文=传) (11-3) 形成样本相关矩阵=开: (11-4) ④求R的特征根入≥方≥.≥元≥0及相应的标准正交化的特征向量4,4,4。,可得 主成分为y=4x0=1,2,.,m) (11-5) [例如11-2]电子工业部所属的15个工厂某年份的经济效益数据如下表11-4。 其中:x一资金利税率(%):x,一固定资产利税率(%):x一流动资金利税率(%):x, 全员利税率(%):x,一成本利税率(%):x。一流动资金周转天数: 表11-4工厂的经济效益指标 厂序 69.87 269.10 94.38 115.74 23.85 66.31 260.00 89.01 93.30 40.09 67.26 272.54 89.29 78.90 26.70 号 4 68.46 250.18 94.24 76.87 24.98 39.45 146.17 54.04 90.95 17.46 109 67 81. 10.4 30.21 31.06 8 31.24 168.31 38.37 62.16 14.29 23.29 109.42 29.59 29.67 8.2% 23.10 92.41 30.80 43.57 12.48 136 1123 17.23 826 27.2 6.38 6 239 14 4.66 18.42 6.24 8.59 4.54 231 15 1.92 9.28 242 333 967 135
7 ①由已知的原始数据矩阵 Xn¥m 计算样本均值向量 1 2 ˆ ( , , , ) T m m = x = x x L x ;(11-1) 其中 1 1 ( 1,2, , ) n i ij j x x i m n = = Â = L ②计算样本协方差矩阵 1 ˆ ( ) ˆ ( ) 1 V ij ij s n = = s - (11-2) 其中 1 ( )( ) ( , 1, 2, , ) n ij li i lj j l s x x x x i j m = = Â - - = L ③把原始数据标准化,即 ij j ij jj x x x s - % = ,记 ( ) Xn m ij x ¥ = % % 。 (11-3) 形成样本相关矩阵 ˆ T R = X% X% ; (11-4) ④求 Rˆ 的特征根 1 2 0 l ³ l ³L ³ lm ³ 及相应的标准正交化的特征向量 1 2 , , , m u u L u ,可得 主成分为 ( 1, 2, , ) T i i y = u x i = L m 。 (11-5) [例如 11-2]电子工业部所属的 15 个工厂某年份的经济效益数据如下表 11-4。 其中: 1 x —资金利税率(%); 2 x —固定资产利税率(%); 3 x —流动资金利税率(%); 4 x — 全员利税率(%); 5 x —成本利税率(%); 6 x —流动资金周转天数; 表 11-4 工厂的经济效益指标 厂序 1 x 2 x 3 x 4 x 5 x 6 x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 69.87 269.10 94.38 115.74 23.85 74 66.31 260.00 89.01 93.30 40.09 80 67.26 272.54 89.29 78.90 26.70 84 68.46 250.18 94.24 76.87 24.98 18 39.45 146.17 54.04 90.95 17.46 109 24.82 116.86 31.51 81.59 10.42 117 30.21 73.60 51.23 39.52 31.06 227 31.24 168.31 38.37 62.16 14.29 129 23.29 109.42 29.59 29.67 8.23 99 23.10 92.41 30.80 43.57 12.48 136 18.95 57.63 28.24 21.91 17.23 231 8.65 21.71 14.35 9.63 8.26 177 5.10 27.27 6.38 8.60 6.46 239 4.66 18.42 6.24 8.59 4.54 231 1.92 9.28 2.42 3.33 9.67 135

按照上述步骤,可以计算出样本相关矩阵为 0.978 1 R= 0.995 0.954 0.880 0.895 0.862 1 0.008 0.724 0.842 0.643 1 -0759-0805 -0.720 -0.730-0.4081 R的特征根及相应的标准正交化的特征向量分别为 表11-5特征向量表 特征向量 5.0390 0.441 0.4370.4360.4100.359 -0.358 83.7 0.6230 0.083 -0.092 0.175 -0.184 0.667 0.678 94.5 0.1030 0.013 0.057-0.006 0.737 -0.360 0.568 97.5 -036 -0.401 00.347 0.501 0.502 -0.285 0.17 075 0.554 0.050 -010 -0.095 0.0004 0.796-0.243 -0.551-0.002 -0.0030.006 100 第一个主成分为 =0.441x+0.437x+0.436x+0.41x,+0.359x,-0.358x。 第二个主成分为 =0.083x-0.092x+0.175x-0.184x,+0.677x+0.678x 此主成分主要反映后两个经济指标的效果。 由于前两个主成分的累计贡献率已达94.%,因此可以选取片,片来评价这些工厂的 综合经济效益。 很显然,用Y,乃,两个综合指标来代替原来的6个指标,起到了精简指标的作用。 11.2. 无量纲化处理方法 评价指标体系之后,由于各评价指标的量纲不同而无法进行直接汇总,为此必须在完 成数据收集之后进行消除量纲的处理。比较常用的有以下三种: 1.相对化处理法 相对化处理法是一种比较简单和实用的方法,易于理解,计算简便。这种方法是先对 每一个评价指标确定一个标准值,然后用各评价指标的实际值(X,)与该指标的标准值进行 比较,得到一个无名数的比值。一般可用参评单位某一时期的平均值或最优值作为标准值。 根据研究目的不同,也可以选择国际先进水平、国内先进水平、历史最高水平或计划规定水 平等作为标准值。通过实际值与标准值的比较,可以将不同性质、不能同度量的各种评价指 标换算成可以进行同度量的评价指标
8 按照上述步骤,可以计算出样本相关矩阵为 1 0.978 1 0.995 0.954 1 ˆ 0.880 0.895 0.862 1 0.008 0.724 0.842 0.643 1 0.759 0.805 0.720 0.730 0.408 1 R Ê ˆ Á ˜ Á ˜ Á ˜ = Á ˜ Á ˜ Á ˜ Á ˜ Ë- - - - - ¯ Rˆ 的特征根及相应的标准正交化的特征向量分别为 表 11-5 特征向量表 l i 特征向量 累计贡献率 (%) 5.0390 0.6230 0.1030 0.1030 0.0260 0.0004 0.441 0.437 0.436 0.410 0.359 -0.358 0.083 -0.092 0.175 -0.184 0.667 0.678 0.013 0.057 -0.006 0.737 -0.360 0.568 -0.364 -0.401 -0.347 0.501 0.502 -0.285 0.177 -0.757 0.554 0.050 -0.170 -0.095 0.796 -0.243 -0.551 -0.002 -0.003 0.006 83.7 94.5 97.5 99.5 99.9 100 第一个主成分为 1 1 2 3 4 5 6 y = 0.441x + 0.437x + 0.436x + 0.41x + 0.359x - 0.358x 第二个主成分为 1 1 2 3 4 5 6 y = 0.083x - 0.092x + 0.175x - 0.184x + 0.677x + 0.678x 此主成分主要反映后两个经济指标的效果。 由于前两个主成分的累计贡献率已达 94.5%,因此可以选取 1 y , 2 y 来评价这些工厂的 综合经济效益。 很显然,用 1 2 Y ,Y 两个综合指标来代替原来的 6 个指标,起到了精简指标的作用。 11.2.2 无量纲化处理方法 评价指标体系之后,由于各评价指标的量纲不同而无法进行直接汇总,为此必须在 完 成数据收集之后进行消除量纲的处理。比较常用的有以下三种: 1.相对化处理法 相对化处理法是一种比较简单和实用的方法,易于理解,计算简便。这种方法是先对 每一个评价指标确定一个标准值,然后用各评价指标的实际值( ) Xi 与该指标的标准值进行 比较,得到一个无名数的比值。一般可用参评单位某一时期的平均值或最优值作为标准值。 根据研究目的不同,也可以选择国际先进水平、国内先进水平、历史最高水平或计划规定水 平等作为标准值。通过实际值与标准值的比较,可以将不同性质、不能同度量的各种评价指 标换算成可以进行同度量的评价指标

在比较时,由于评价指标有“正”、“逆”之分,相应的无量纲化处理方法也有两种情 况:1)正指标是指指标数值越大越好的指标,如产值、利润及利润率、全员劳动生产率等 2)逆指标是指指标数值越小越好的指标,如单位产品成木、单位产品能耗、流动资金周转 天数等。若将处理后的值记为X,,则相对化处理的计算公式为: 正指标相对化处理公式:X=立 (11-6) 逆指标相对化处理公式:X=多 (11-7) [例如11-3]假定要对某市五个地区某个时期的工业企业经济效益指标进行相对化处 理。己知这五个地区的工业企业经济效益指标实际值如表11-7所示,假设以该地区同期所 有工业企业各指标平均值作为标准值。 表11-7 工业企业经济效益表 计量 标准值 指标名称及代号 单位 甲地区乙地区丙地区丁地区戊地区所有地区 产品销售率(X)% 96.0195.7298.4293.4395.1697.03 资金利税率(X) 14.99.2113.88 10.7510.25 12.85 成本利润率() 9.5 3.35 7.55 3.99 5.03 6.74 劳动生产率(X,) 元/人 14830 1000415545970814590 13985 流动资金周转 次数(X) 1.68 1.79 1.8 2.21 1.87 1.83 净产值率(X) % 28.426.4825.5622.325.0126.35 现对各指标进行相对化处理。由于表11-7中6个评价指标皆为正指标,故将各工业合 业的各指标实际值与其标准值相比即可。将标准值和处理后的值一并列入表1山-8。 表11-8 相对化处理计算表 计量 标准化值 指标名称及代号 单位 企业1企业2企业3企业4企业5 产品销售率(X) 98.95 98.65 101.43 96.29 98.07 资金利税率(X) 115.95 71.67 108.02 83.6679.77 成本利润率(X) % 140.9549.70112.0259.2074.63 劳动生产率(X,) 106.0471.53111.1569.42104.33 流动资金周转次数(X) 91.8097.8198.36 120.77102.19 净产值率(X) %107.78100.4997.0084.6394.91 2.函数化处理法 函救化外理方法又称为功效系数法其特占是利用特定的方法将每一个指标的实际值 转化为用百分制表示的分值。这种方法不仅可以对每 指标的好坏优劣作出直观的判断,还 可以解决不同性质的指标综合问题。而且不论正指标还是逆指标,都可以用同一个公式去处 理,解决了前一种方法正逆指标必须使用不同公式的不便。函数化处理的步骤如下: ()对每个指标两个阀值(临界值),其中一个为上限值,又称为满意值,记为X上,另 9
9 在比较时,由于评价指标有“正” 、 “ 逆”之分,相应的无量纲化处理方法也有两种情 况:1)正指标是指指标数值越大越好的指标,如产值、利润及利润率、全员劳动生产率等; 2)逆指标是指指标数值越小越好的指标,如单位产品成本、单位产品能耗、流动资金周转 天数等。若将处理后的值记为 X i ,则相对化处理的计算公式为: 正指标相对化处理公式: ' i i m X X X = (11-6) 逆指标相对化处理公式: ' m i i X X X = (11-7) [例如 11-3]假定要对某市五个地区某个时期的工业企业经济效益指标进行相对化处 理。已知这五个地区的工业企业经济效益指标实际值如表 11-7 所示,假设以该地区同期所 有工业企业各指标平均值作为标准值。 表 11-7 工业企业经济效益表 实 际 值 标准值 指标名称及代号 计 量 单 位 甲地区 乙地区 丙地区 丁地区 戊地区 所有地区 产品销售率(X1) % 96.01 95.72 98.42 93.43 95.16 97.03 资金利税率(X2) % 14.9 9.21 13.88 10.75 10.25 12.85 成本利润率(X3) % 9.5 3.35 7.55 3.99 5.03 6.74 劳动生产率(X4) 元/人 14830 10004 15545 9708 14590 13985 流动资金周转 次数(X5) 次 1.68 1.79 1.8 2.21 1.87 1.83 净产值率(X6) % 28.4 26.48 25.56 22.3 25.01 26.35 现对各指标进行相对化处理。由于表 11-7 中 6 个评价指标皆为正指标,故将各工业企 业的各指标实际值与其标准值相比即可。将标准值和处理后的值一并列入表 11-8。 表 11-8 相对化处理计算表 标准化值 指标名称及代号 计 量 单 位 企业 1 企业 2 企业 3 企业 4 企业 5 产品销售率(X1) % 98.95 98.65 101.43 96.29 98.07 资金利税率(X2) % 115.95 71.67 108.02 83.66 79.77 成本利润率(X3) % 140.95 49.70 112.02 59.20 74.63 劳动生产率(X4) % 106.04 71.53 111.15 69.42 104.33 流动资金周转次数(X5) % 91.80 97.81 98.36 120.77 102.19 净产值率(X6) % 107.78 100.49 97.00 84.63 94.91 2.函数化处理法 函数化处理方法又称为功效系数法,其特点是利用特定的方法将每一个指标的实际值 转化为用百分制表示的分值。这种方法不仅可以对每一指标的好坏优劣作出直观的判断,还 可以解决不同性质的指标综合问题。而且不论正指标还是逆指标, 都可以用同一个公式去处 理,解决了前一种方法正逆指标必须使用不同公式的不便。函数化处理的步骤如下: (1)对每个指标两个阈值(临界值),其中一个为上限值,又称为满意值,记为 X上 ,另
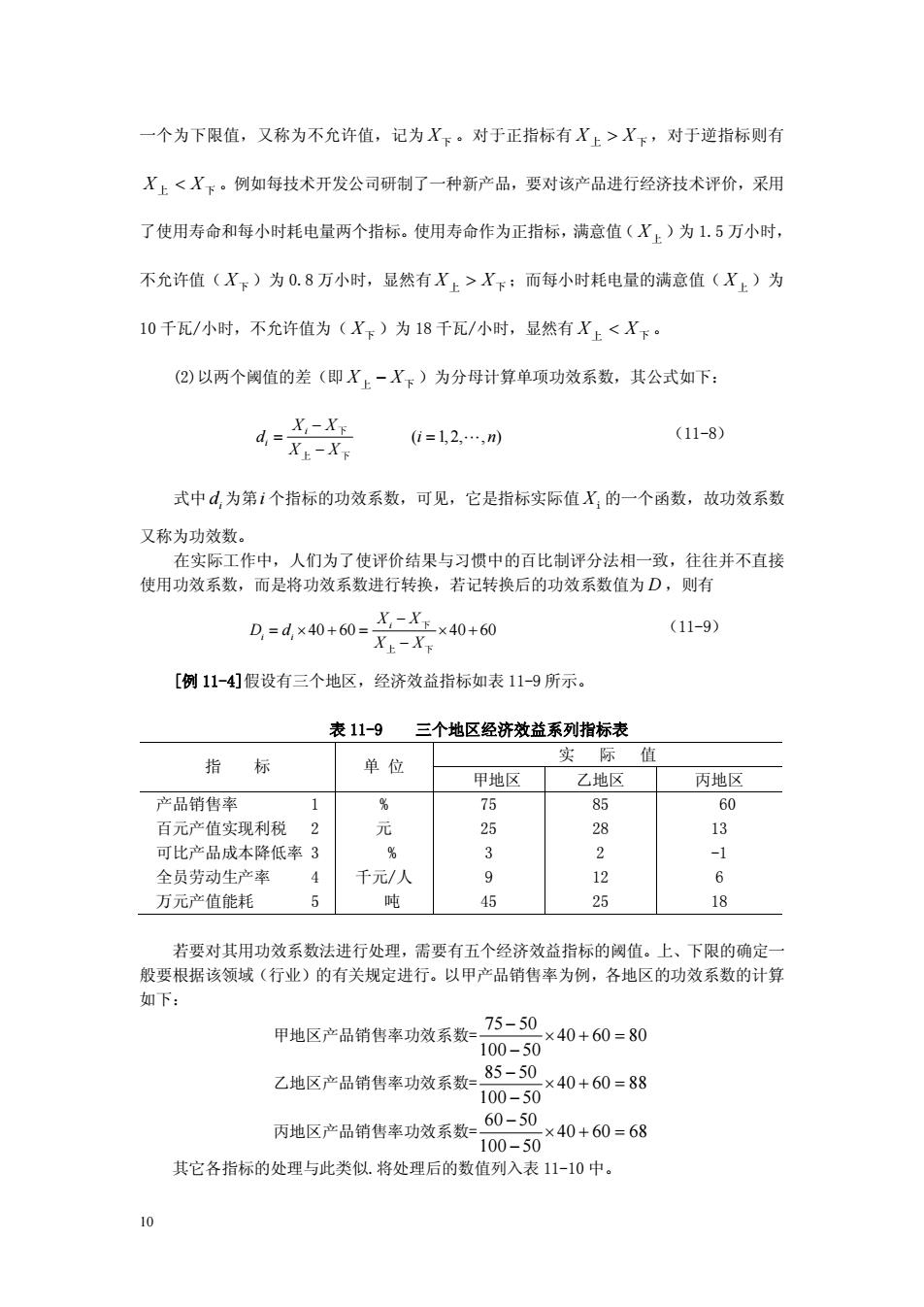
一个为下限值,又称为不允许值,记为X。对于正指标有X,>X。,对于逆指标则有 X上X下:而每小时耗电量的满意值(X上)为 10千瓦/小时,不允许值为(Xx)为18千瓦/小时,显然有X上<Xx。 (②)以两个阅值的差(即X上-X下)为分母计算单项功效系数,其公式如下: X上-XF =12.,n) (11-8) 式中,为第i个指标的功效系数,可见,它是指标实际值X,的一个函数,故功效系数 又称为功效数: 车实际工作中,人们为了使评价结果与习惯中的百比制评分法相一致,往往并不直接 使用功效系数,而是将功效系数进行转换,若记转换后的功效系数值为D,则有 D=d×40+60=X-X×40+60 (11-9) X上-X [例11-4]假设有三个地区,经济效益指标如表11-9所示。 表11-9三个地区经济效益系列指标表 指标 单位 实际值 甲地风 /地区 丙地区 产品销售率 85 百元产值实现利税 25 13 可比产品成本降低率3 3 2 -1 全员劳动生产率 千元/人 9 12 6 万元产值能耗 吨 45 25 18 若要对其用功效系数法进行处理,需要有五个经济效益指标的阅值。上、下限的确定 般要根据该领域(行业)的有关规定进行。以甲产品销售率为例,各地区的功效系数的计算 如下: 甲地区产品销售率功微系数:75-50 40+60=80 100-50 乙地区产品销售率功效系数=85-50×40+60=88 100-50 60-50 丙地区产品销售率功效系数100二0×40+60=68 其它各指标的处理与此类似.将处理后的数值列入表11-10中
10 一个为下限值,又称为不允许值,记为 X下 。对于正指标有 X 上 > X 下 ,对于逆指标则有 X 上 X 下 ;而每小时耗电量的满意值( X上 )为 10 千瓦/小时,不允许值为( X下 )为 18 千瓦/小时,显然有 X 上 < X 下 。 (2)以两个阈值的差(即 X 上 - X下 )为分母计算单项功效系数,其公式如下: ( 1, 2, , ) i i X X d i n X X - = = - L 下 上 下 (11-8) 式中 i d 为第i 个指标的功效系数,可见,它是指标实际值 Xi 的一个函数,故功效系数 又称为功效数。 在实际工作中,人们为了使评价结果与习惯中的百比制评分法相一致,往往并不直接 使用功效系数,而是将功效系数进行转换,若记转换后的功效系数值为 D ,则有 40 60 40 60 i i i X X D d X X - = ¥ + = ¥ + - 下 上 下 (11-9) [例 11-4]假设有三个地区,经济效益指标如表 11-9 所示。 表 11-9 三个地区经济效益系列指标表 实 际 值 指 标 单 位 甲地区 乙地区 丙地区 产品销售率 1 百元产值实现利税 2 可比产品成本降低率 3 全员劳动生产率 4 万元产值能耗 5 % 元 % 千元/人 吨 75 25 3 9 45 85 28 2 12 25 60 13 -1 6 18 若要对其用功效系数法进行处理,需要有五个经济效益指标的阈值。上、下限的确定一 般要根据该领域(行业)的有关规定进行。以甲产品销售率为例,各地区的功效系数的计算 如下: 甲地区产品销售率功效系数= 75 50 40 60 80 100 50 - ¥ + = - 乙地区产品销售率功效系数= 85 50 40 60 88 100 50 - ¥ + = - 丙地区产品销售率功效系数= 60 50 40 60 68 100 50 - ¥ + = - 其它各指标的处理与此类似.将处理后的数值列入表 11-10 中