
第7章统计假设检验 学习目标 1、理解假设检验的基本思想和基本步骤: 2、理解假设检验的两类错误及其关系: 3、熟练掌握总体平均数、总体成数和总体方差的各种假设检验方法 4、利用P一值进行假设检验 基本概念 假设检验单边检验双侧检验P值检验总体平均数的假设检验总体成数的假 设检验总体方差的假设检验 7.1假设检验的基本问题 假设检验是统计推断的另一种形式,和估计一样要通过样本取得数据,对总体做出推断。 估计是通过样本的观察结果来推断未知总体参数的取值范围和做出结论的可靠程度,而假设 检验是预先对总体参数的取值做出假定,然后用样本数据验证,做出接受还是拒绝原来假设 的结论。当然由于样木的随机性,这种推断也同样 一定风险。先提出假设 后加以论证 再决定取合是科学研究中常用的方法之一。统计的假设检验可以作为帮助研究人员和管理 员决策的一种手段。例如工业产品的质量管理就是应用了这一方法。质量控制图假设在正常 的情况下所生产的产品的某一质量指标是围绕其平均值“的上下微小变动,然后每隔一段 时间抽验一定的产品样本,如果符合假设的要求,就视为正常,殊续生产。如样本数据出现 了变化,过高或过低,与原假设不符,那就要停止生产,检查原因,以避免生产次品。 7.1.1假设检验的基本思想 从一个简单的实例谈起。 【例7-1】有一厂家生产了两批灯泡各10000只,其中一批有9999只是好的,仅有 只是坏的,而另一批灯泡恰好相反,有9999只是坏的,仅有1只是好的,现卖给某一商场 据说这是好的那 可商场从这批灯泡中任抽一只发觉是坏的,于是拒绝买下这批货物 商场拒买的理由是什么呢 商场拒买的理由是:假设这批灯泡是好的那批,那么“任抽一只是坏的”这样的随机事 件发生的概率应是0.01%,这样小的概率在一次抽样中几乎不可能发生,而今任抽一只是 坏的,这样的事件居然发生了,于是拒绝接受“这是好的那批”的假设,可以肯定地认为将 买到坏的那批 于是坚决拒买。 统计学中的假设检验(ypothesis Test)的基本思想,就是人们经常在实际中采用的 这样一个朴素道理。这相当于一个带有概率性质的反证法:先假定一个假设是成立的,在这 种假设下,将构成一个小概率事件,根据实际推断原理:“小概率事件在一次试验中几乎是 不可能发生的”。然而这样的事件在一次试验中却发生了,那么我们自然要怀疑“霞设:的 正确性了,于是“拒绝假设”。如果“小概率事件”末发生,则不能拒绝“假设”,而只能接 受它 或许有人要问,如果厂家确实卖的是好的那批灯泡,而恰好(万分之一的可能性)抽取的 是那仅有的一只坏灯泡呢?这里要强调的是,我们用的是实际推断原理,即小概率事件在一 次试验中,实际处理上认为它不可能发生。就好像偶尔有汽车冲到人行道上,但人们照常上
1 第 7 章 统计假设检验 学习目标 1、理解假设检验的基本思想和基本步骤; 2、理解假设检验的两类错误及其关系; 3、熟练掌握总体平均数、总体成数和总体方差的各种假设检验方法; 4、利用 P - 值进行假设检验; 基本概念 假设检验 单边检验 双侧检验 P 值检验 总体平均数的假设检验 总体成数的假 设检验 总体方差的假设检验 7.1 假设检验的基本问题 假设检验是统计推断的另一种形式, 和估计一样要通过样本取得数据, 对总体做出推断。 估计是通过样本的观察结果来推断未知总体参数的取值范围和做出结论的可靠程度, 而假设 检验是预先对总体参数的取值做出假定, 然后用样本数据验证,做出接受还是拒绝原来假设 的结论。当然由于样本的随机性,这种推断也同样有一定风险。先提出假设,后加以论证, 再决定取舍是科学研究中常用的方法之一。 统计的假设检验可以作为帮助研究人员和管理人 员决策的一种手段。例如工业产品的质量管理就是应用了这一方法。质量控制图假设在正常 的情况下所生产的产品的某一质量指标是围绕其平均值 m 的上下微小变动,然后每隔一段 时间抽验一定的产品样本,如果符合假设的要求,就视为正常,继续生产。如样本数据出现 了变化,过高或过低,与原假设不符,那就要停止生产,检查原因,以避免生产次品。 7.1.1 假设检验的基本思想 从一个简单的实例谈起。 【例 7-1】有一厂家生产了两批灯泡各 10 000 只,其中一批有 9 999 只是好的,仅有一 只是坏的,而另一批灯泡恰好相反,有 9 999 只是坏的,仅有 1 只是好的,现卖给某一商场, 据说这是好的那一批,可商场从这批灯泡中任抽一只发觉是坏的,于是拒绝买下这批货物。 商场拒买的理由是什么呢? 商场拒买的理由是:假设这批灯泡是好的那批,那么“任抽一只是坏的”这样的随机事 件发生的概率应是 0.01%,这样小的概率在一次抽样中几乎不可能发生,而今任抽一只是 坏的,这样的事件居然发生了,于是拒绝接受“这是好的那批”的假设,可以肯定地认为将 买到坏的那批,于是坚决拒买。 统计学中的假设检验(Hypothesis Test)的基本思想,就是人们经常在实际中采用的 这样一个朴素道理。这相当于一个带有概率性质的反证法:先假定一个假设是成立的,在这 种假设下,将构成一个小概率事件,根据实际推断原理: “小概率事件在一次试验中几乎是 不可能发生的” 。然而这样的事件在一次试验中却发生了,那么我们自然要怀疑“假设”的 正确性了,于是“拒绝假设” 。如果“小概率事件”末发生,则不能拒绝“假设” ,而只能接 受它。 或许有人要问,如果厂家确实卖的是好的那批灯泡,而恰好(万分之一的可能性)抽取的 是那仅有的一只坏灯泡呢?这里要强调的是,我们用的是实际推断原理,即小概率事件在一 次试验中,实际处理上认为它不可能发生。就好像偶尔有汽车冲到人行道上,但人们照常上

街一样。如果厂家卖的是好的那一批,而仅抽一次是坏的,这种可能性是万分之一,即抽 万次才发生一次。这也正是为什么叫带有概率性质的反证法的原因。它区别于一般反证法 一般反证法用的是形式辑中的绝对矛盾。也正是基于这个原因,以后每次进行假设检验时, 总是要把这个 “意外”的 小概率告诉出来,即所谓的“显著性水平”,它表示假设检验发生 意外或“犯错误”的可能性。 概率小到什么程度才叫“小概率事件呢”?这要视具体情况而定。在例7-1中,如果 灯泡是100只一批,任抽一只是坏的,也应拒买,即百分之一也是小概率。在实际运用中, 通常把概率不超过0.05的事件当作“小概率事件”。 7.1.2假设检验中的一些基本概念 1.原假设和备择假设 在假设检验的一开始,首先要提出一个假设,就称作原假设,又称零假设或虚拟假设等, 通常用H表示。比如,在质量管理中假设在正常的情况下,零件的平均长度应是2匣米, 就建立H。:μ=2厘米。在提出原假设的同时,还要制定另一个假设称做备择假设。原假设 是待检验的假设,备择假设则是原假设被拒绝后替换的假设。因为对于任何一个假设检验问 题所有可能的结果都应包含在两个假设之内,非此即彼。如上面质量管理的例子中,零件的 平均长度要么等于2厘米,要么不等于2厘米,备择假设通常用h表示,因此可以建立H, ≠2厘米。 2.检验统计量 对原假设检验时必然要根据样本的数据来判断。对样本数据进行加工并用来判断是否接 受原假设的统计量称做检验统计量,如上面列举的原假设H。:μ=μ。(μ。为一已知数值), 那么样本均值x就可以作为检验统计量,有时为了方便还将样本均值进一步加工,如样本均 值服从正态分布时将样本均值标准化,Z=工一 口作为检验统计量,简称Z统计量,或者 o/Vn 根据条件用【=【二凸称作1统计量。统计量的选择要根据研究的参数及其估计量的分布、 抽样的方式、总体方差是否已知等多种因素来确定。 3接域和编域 假设检验根据检验统计量的具体结果来判断是否接受,因此在假设伍为真的情况下 将抽样所有可能结果组成的样本空间划分为两部分,一部分是原假设为真时允许范围内的变 动,应该接受原假设,因此称作接受域:另一部分是超出了一定的界限,当原假设为真时只 有很小的概率出现,因而当统计量的结果落入这一区域便应拒绝原假设,这一区域便称作拒 绝域。接受域和拒绝域之间的分割点通常称作临界值。为直观地说明接受域和拒绝域,见图 7-1所示。 2
2 街一样。如果厂家卖的是好的那一批,而仅抽一次是坏的,这种可能性是万分之一,即抽一 万次才发生一次。这也正是为什么叫带有概率性质的反证法的原因,它区别于一般反证法。 一般反证法用的是形式逻辑中的绝对矛盾。 也正是基于这个原因, 以后每次进行假设检验时, 总是要把这个“意外”的小概率告诉出来,即所谓的“显著性水平” ,它表示假设检验发生 意外或“犯错误”的可能性。 概率小到什么程度才叫“小概率事件呢”?这要视具体情况而定。在例 7-1 中,如果 灯泡是 100 只一批,任抽一只是坏的,也应拒买,即百分之一也是小概率。在实际运用中, 通常把概率不超过 0.05 的事件当作“小概率事件” 。 7.1.2 假设检验中的一些基本概念 1.原假设和备择假设 在假设检验的一开始, 首先要提出一个假设, 就称作原假设, 又称零假设或虚拟假设等, 通常用 H 0 表示。比如,在质量管理中假设在正常的情况下,零件的平均长度应是 2 厘米, 就建立 H 0 :μ=2 厘米。在提出原假设的同时,还要制定另一个假设称做备择假设。原假设 是待检验的假设,备择假设则是原假设被拒绝后替换的假设。因为对于任何一个假设检验问 题所有可能的结果都应包含在两个假设之内,非此即彼。如上面质量管理的例子中,零件的 平均长度要么等于 2 厘米, 要么不等于 2 厘米,备择假设通常用 H1表示, 因此可以建立 H 1 : μ≠2 厘米。 2.检验统计量 对原假设检验时必然要根据样本的数据来判断。 对样本数据进行加工并用来判断是否接 受原假设的统计量称做检验统计量,如上面列举的原假设 H 0 :μ=μ0(μ0为一已知数值), 那么样本均值 x 就可以作为检验统计量,有时为了方便还将样本均值进一步加工,如样本均 值服从正态分布时将样本均值标准化, n x Z / 0 s - m = 作为检验统计量,简称 Z 统计量,或者 根据条件用 s n x t / - m 0 = 称作t 统计量。统计量的选择要根据研究的参数及其估计量的分布、 抽样的方式、总体方差是否已知等多种因素来确定。 3.接受域和拒绝域 假设检验根据检验统计量的具体结果来判断是否接受 H0,因此在假设 H0 为真的情况下 将抽样所有可能结果组成的样本空间划分为两部分, 一部分是原假设为真时允许范围内的变 动,应该接受原假设,因此称作接受域;另一部分是超出了一定的界限,当原假设为真时只 有很小的概率出现,因而当统计量的结果落入这一区域便应拒绝原假设,这一区域便称作拒 绝域。接受域和拒绝域之间的分割点通常称作临界值。为直观地说明接受域和拒绝域,见图 7-1 所示
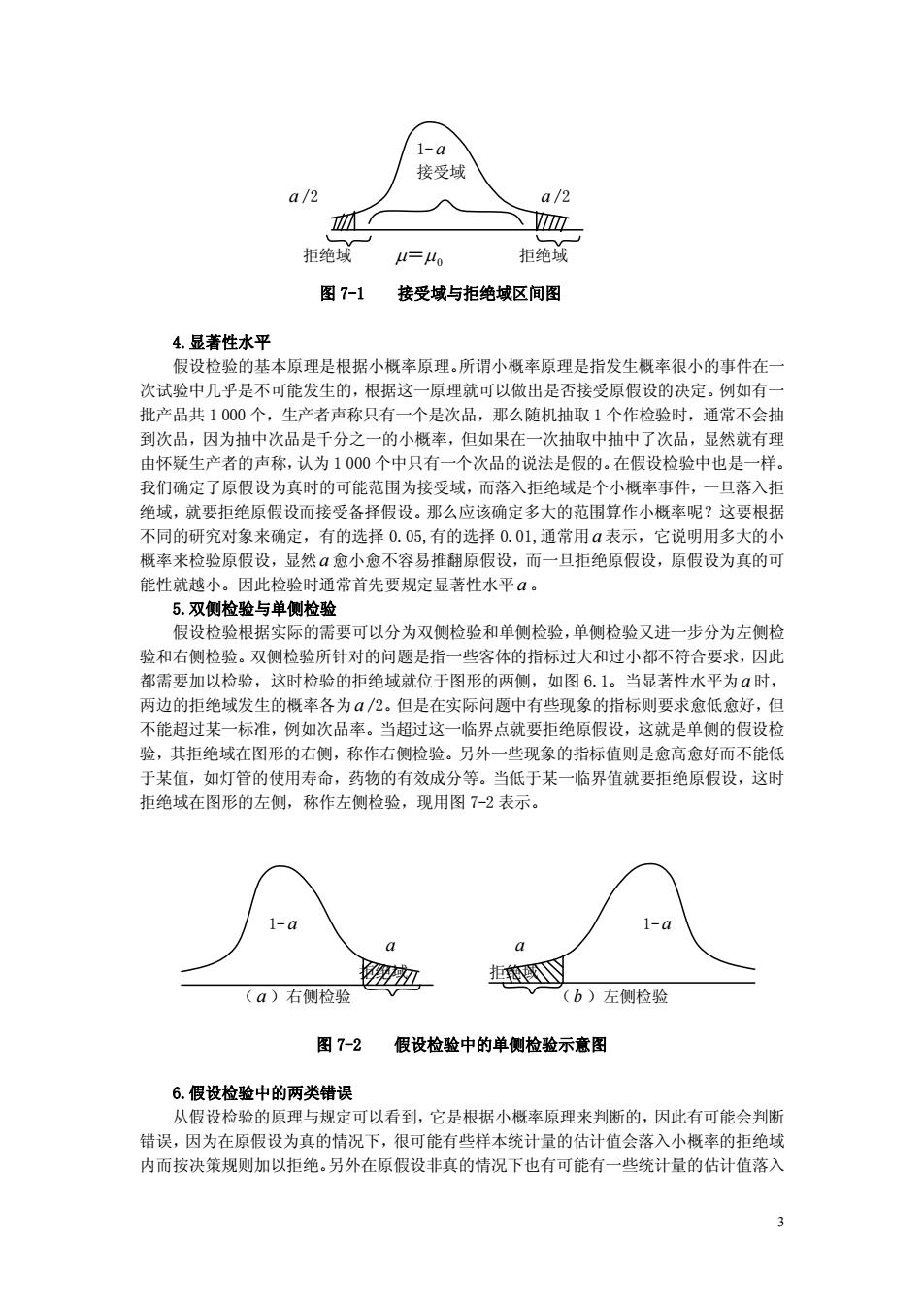
接受域 a/2 a/2 M T证 拒绝域 =4 拒绝域 图7-1 接受域与拒绝域区间图 4.显著性水平 假设检验的基本原理是根据小概率原理。所谓小概率原理是指发生概率很小的事件在一 次试验中几乎是不可能发生的,根据这一原理就可以做出是否接受原假设的决定。例如有 册产品址1000个,生产者声称只口有一个是次品。那么随机抽取1个作拾盼时,通常不△村 到次品,因为抽中次品是干分之 的小概率,但如果 次 取中抽 了次 品 显然就有 由怀疑生产者的声称,认为1000个中只有一个次品的说法是假的。在假设检验中也是一样。 我们确定了原假设为真时的可能范用为接受域,而落入拒绝域是个小概率事件, 一且落入拒 绝域,就要拒绝原假设而接受备择假设。那么应该确定多大的范围算作小概率呢?这要根据 不同的研究对象来确定,有的选择0.05,有的选择0.01,通常用a表示,它说明用多大的小 概率来检验原假设,显然a 翻原假设,而一旦拒绝原假设,原假设为真的可 能性就越小。因此检验时通常首先要规定显著性水平α。 5.双侧检验与单侧检验 假设检验根据实际的需要可以分为双侧检验和单侧检验,单侧检验又进一步分为左侧检 验和右侧检验。双测检验所针对的问顾是指一些客体的指标过大和过小都不符合要求,因此 都需加以拾。这时拾哈的拓饰域就位干图形的两侧。如图61。当品性水平为a时 两边的拒绝域发生的概率各为α/2。但是在实际问题中有些现象的指标则要 愈低愈好,但 不能超过某一标准,例如次品率。当超过这一临界点就要拒绝原假设,这就是单侧的假设检 验,其拒绝域在图形的右侧,称作右侧检验。另外一些现象的指标值则是愈高愈好而不能低 于某值,如灯管的使用寿命,药物的有效成分等。当低于某一临界值就要拒绝原假设,这时 拒绝域在图形的左侧,称作左侧检验,现用图7-2表示。 - (a)右侧检验 挺 (b)左侧检验 图7-2 假设检验中的单侧检验示意图 6.假设检验中的两类错误 从假设检验的原理与规定可以看到,它是根据小概率原理来判断的,因此有可能会判断 错误,因为在原假设为真的情况下,很可能有些样本统计量的估计值会落入小概*的拒绝域 内而按决策规则加以拒绝。另外在原假设非真的情况下也有可能有一些统计量的估计值落入
3 1- a 接受域 a /2 a /2 拒绝域 m= m 0 拒绝域 图 7-1 接受域与拒绝域区间图 4.显著性水平 假设检验的基本原理是根据小概率原理。 所谓小概率原理是指发生概率很小的事件在一 次试验中几乎是不可能发生的, 根据这一原理就可以做出是否接受原假设的决定。例如有一 批产品共 1 000 个,生产者声称只有一个是次品,那么随机抽取 1 个作检验时,通常不会抽 到次品,因为抽中次品是千分之一的小概率,但如果在一次抽取中抽中了次品,显然就有理 由怀疑生产者的声称, 认为 1 000 个中只有一个次品的说法是假的。 在假设检验中也是一样。 我们确定了原假设为真时的可能范围为接受域,而落入拒绝域是个小概率事件,一旦落入拒 绝域,就要拒绝原假设而接受备择假设。那么应该确定多大的范围算作小概率呢?这要根据 不同的研究对象来确定,有的选择 0.05,有的选择 0.01,通常用a 表示,它说明用多大的小 概率来检验原假设,显然a 愈小愈不容易推翻原假设,而一旦拒绝原假设,原假设为真的可 能性就越小。因此检验时通常首先要规定显著性水平a 。 5.双侧检验与单侧检验 假设检验根据实际的需要可以分为双侧检验和单侧检验, 单侧检验又进一步分为左侧检 验和右侧检验。双侧检验所针对的问题是指一些客体的指标过大和过小都不符合要求,因此 都需要加以检验,这时检验的拒绝域就位于图形的两侧,如图 6.1。当显著性水平为a 时, 两边的拒绝域发生的概率各为a /2。但是在实际问题中有些现象的指标则要求愈低愈好,但 不能超过某一标准,例如次品率。当超过这一临界点就要拒绝原假设,这就是单侧的假设检 验,其拒绝域在图形的右侧,称作右侧检验。另外一些现象的指标值则是愈高愈好而不能低 于某值,如灯管的使用寿命,药物的有效成分等。当低于某一临界值就要拒绝原假设,这时 拒绝域在图形的左侧,称作左侧检验,现用图 7-2 表示。 1- a 1- a a a 拒绝域 拒绝域 ( a )右侧检验 (b )左侧检验 图 7-2 假设检验中的单侧检验示意图 6.假设检验中的两类错误 从假设检验的原理与规定可以看到,它是根据小概率原理来判断的,因此有可能会判断 错误,因为在原假设为真的情况下,很可能有些样本统计量的估计值会落入小概率的拒绝域 内而按决策规则加以拒绝。 另外在原假设非真的情况下也有可能有一些统计量的估计值落入

接受域的范围之内而接受原假设。因此可以把这些情况归结为两类错误。第一类错误是指原 罗设山为直而却被拒绝的错误,它是犯了弃直的错误,犯错误的概率试是a,所以也叫a错 误或第一类错误。第二类错误是指原假设为非真而却予以接受的错误,这是一种取伪的 错误,这种错误发生的概率通常用B表示 故也称B错误或第 类错误 在生产者将产品 给消费者时,通常要进行产品的质量检验,原假设总是产品是合格的,但检验时生产者总是 担心把合格品检验为不合格品,也就是第一类错误a,所以a也称为生产者风险。而在消费 者一方却恐怕把不合格品检验不出来当作合格品而接受,因而第二类错误B也称为消费者风 险。通常的假设检验只规定第一类错误,即显著性水平,而不考虑第二类错误B,并称这 样的检验为显著性检验。要设计一个好的检验方案应既要限制误,又要限制B错误。关 于两类错误的关系可以用表加以归纳和图加以显示。 表7-1 假设检验统计决策表 H。为真 H,为假 接受H。拒绝H 正确(1-a) 取伪B 拒绝H。接受H 弃真a 正确(1-B) 物Z 图7-3H。:4=4时两类错误示意图 7.1.3假设检验的一般步骤 1.根据研究问题的需要建立原假设H。和备择假设H, 由于假设检验是利用小概率原理来否定原假设,因此原假设总是与等号在一起。以均值 的假设检验为例,不外乎三种情况: (1)H。:F4o:H1:4≠4o: (2)H。:4≥4o:H1:I4. 其中(1)为双侧假设检验:(2)为左侧假设检验:(3)为右侧假设检验。采用哪一种 检验要视研究的目的而定,尤其是在左侧检验和右侧检验时,放在马或H,的不同位置往往 4
4 接受域的范围之内而接受原假设。因此可以把这些情况归结为两类错误。第一类错误是指原 假设 H0为真而却被拒绝的错误,它是犯了弃真的错误,犯错误的概率就是a ,所以也叫a 错 误或第一类错误。第二类错误是指原假设 H0 为非真而却予以接受的错误,这是一种取伪的 错误,这种错误发生的概率通常用β表示,故也称β错误或第二类错误。在生产者将产品售 给消费者时,通常要进行产品的质量检验,原假设总是产品是合格的,但检验时生产者总是 担心把合格品检验为不合格品,也就是第一类错误a ,所以a 也称为生产者风险。而在消费 者一方却恐怕把不合格品检验不出来当作合格品而接受, 因而第二类错误β也称为消费者风 险。通常的假设检验只规定第一类错误a ,即显著性水平,而不考虑第二类错误β,并称这 样的检验为显著性检验。要设计一个好的检验方案应既要限制a 错误,又要限制β错误。关 于两类错误的关系可以用表加以归纳和图加以显示。 表 7-1 假设检验统计决策表 H 0 为真 H 0 为假 接受 H 0 拒绝 H 1 正确(1- a ) 取伪β 决 策 拒绝 H 0 接受 H 1 弃真a 正确(1-β) m 0 图 7-3 H 0 ﹕ m = m 0 时两类错误示意图 7.1.3 假设检验的一般步骤 1. 根据研究问题的需要建立原假设 H 0 和备择假设 H 1 由于假设检验是利用小概率原理来否定原假设,因此原假设总是与等号在一起。以均值 的假设检验为例,不外乎三种情况: (1) H 0 ﹕m= m 0 ; H 1 ﹕m ≠ m 0 ; (2) H 0 ﹕m≥ m 0 ; H 1 ﹕m< m 0 ; (3) H 0 ﹕m≤ m 0 ; H 1 ﹕m> m 0 。 其中(1)为双侧假设检验;(2)为左侧假设检验;(3)为右侧假设检验。采用哪一种 检验要视研究的目的而定,尤其是在左侧检验和右侧检验时,放在 H0或 H 1 的不同位置往往

会得出相反的结论。假设检验中所用的推断方法类似于数学中的反证法,把所希望证明的假 设常常作为备择假设。因为放在H和出在接受时可能犯错误的概率是不同的,放在H。接受 时可能犯的错误是取伪错误,因此是B,通常不容易知道。而放在H,接受时可能犯错误的 概率就是弃真错误的概率α,是可以明确知道的。另外需要说明的是当接受H。时,并不意 味着H。一定正确,而确切地说应该是根据样本数据在显著性水平为α的情况下尚不能推翻 原假设。 2.找出检验统计量及其分布 在建立好假设以后要确定H还是拒绝H都是根据检验统计量的具体结果落入接受域还 是拒绝域而定。这就要确定什么是检验统计量及该统计量服从什么分布。确定检验统计量及 其分布(包括其数学期望和方差)是由许多因素决定的。如检验的是什么参数 总体的分布 形式是否已知,总体的方差是否知道,若检验的参数是两个总体均值之差则还需知道两个总 体的方差是否假定相等。不同的情况要采用不同的统计量,如Z统计量、1统计量、x统 计最及F结计量等算 3.规定显著性水平 规定显著性水平以后,拒绝域也随之而定。显著性水平的大小应根据研究问题所需的精 确度而定,对于接受备择假设而言,如果要求结论比较精确,显著性水平α应该小一些,反 之,要求不太精确,a可稍大一些,可取0.05或0.1。 但是,读者应当注意的是,显著性水平的大小有时会影响假设检验的结果。例如对同一 个总体,当显著性水平a=0.1时拒绝了原假设,当a=0.01时就可能接受原假设。这一点可 以很容易地从图7-4中看出来 0 =0.05 统计量的值 图7-4显著性水平的大小影响假设检验的结果 4.确定决策规则 在规定了显著性水平与选择好检验的统计量后,就可以根据原假设与对立假设的设置情 况找出接受域与拒绝域的临界点。例如统计量若服从正态分布,标准化后的统计量为Z。 当a=0.05双侧检验,其临界值为±1.96。当统计量Z1.96时就应拒绝H。,接受H,。不 同的检验在规则上略有不同,将在后面的介绍中分别说明。 5.根据观察所得到的数据进行计算并做出决策 当然以上的各个步骤有些有先后关系,如先有了假设,确定了检验统计量,才能有决
5 会得出相反的结论。假设检验中所用的推断方法类似于数学中的反证法,把所希望证明的假 设常常作为备择假设。 因为放在 H0和 H1在接受时可能犯错误的概率是不同的,放在 H 0 接受 时可能犯的错误是取伪错误,因此是β,通常不容易知道。而放在 H 1 接受时可能犯错误的 概率就是弃真错误的概率a ,是可以明确知道的。另外需要说明的是当接受 H 0 时,并不意 味着 H 0 一定正确,而确切地说应该是根据样本数据在显著性水平为a 的情况下尚不能推翻 原假设。 2.找出检验统计量及其分布 在建立好假设以后要确定 H0还是拒绝 H0都是根据检验统计量的具体结果落入接受域还 是拒绝域而定。这就要确定什么是检验统计量及该统计量服从什么分布。确定检验统计量及 其分布(包括其数学期望和方差)是由许多因素决定的。如检验的是什么参数,总体的分布 形式是否已知,总体的方差是否知道,若检验的参数是两个总体均值之差则还需知道两个总 体的方差是否假定相等。不同的情况要采用不同的统计量,如 Z 统计量、t 统计量、 2 x 统 计量及 F 统计量等等。 3.规定显著性水平 规定显著性水平以后,拒绝域也随之而定。显著性水平的大小应根据研究问题所需的精 确度而定,对于接受备择假设而言,如果要求结论比较精确,显著性水平a 应该小一些,反 之,要求不太精确,a 可稍大一些,可取 0.05 或 0.1。 但是,读者应当注意的是,显著性水平的大小有时会影响假设检验的结果。例如对同一 个总体,当显著性水平a =0.1 时拒绝了原假设,当a =0.01 时就可能接受原假设。这一点可 以很容易地从图 7-4 中看出来。 0. 05 2 = a 0. 005 2 = a 统计量的值 图 7-4 显著性水平的大小影响假设检验的结果 4.确定决策规则 在规定了显著性水平与选择好检验的统计量后, 就可以根据原假设与对立假设的设置情 况找出接受域与拒绝域的临界点。例如统计量若服从正态分布,标准化后的统计量为 Z 。 当 a =0.05 双侧检验,其临界值为±1.96。当统计量 Z Ò1. 96 时就应拒绝 H 0 ,接受 H 1 。不 同的检验在规则上略有不同,将在后面的介绍中分别说明。 5.根据观察所得到的数据进行计算并做出决策 当然以上的各个步骤有些有先后关系,如先有了假设,确定了检验统计量,才能有决

策的规则,但显著性水平的规定可以先后灵活一些。 7.2总体均值的假设检验 7.2.1Z-检验 1,当总体分布为正态分布,总体标准差0为已知时,检验原假设H。:4=山。当品 成立时,由于总体X~N(4,2):所以样本均值~N(,21)。从而统计量为: 2=F-4 -N(0,1) (7-1) 即它服从标准正态分布,于是可用它来检验原假设 [例7-2】某市历年来对7岁男孩的统计资料表明,他们的身高服从均值为1.32米、标 准差为0.12米的正态分布。现从各个学校随机抽取25个7岁男学生,测得他们平均身高 1.36米,若己知今年全市7岁男孩身高的标准差仍为0.12米,问与历年7岁男孩的身高相 比是否有显著差异(取u=0.05). 解:从题意可知,=1.36米,4,=1.32米,=0.12米 ()建立假设:H:4=1.32,H:4≠1.32 (②)确定统计量: Z=-4=136-1.32 o/W6012/W25=167 (3)Z的分布:Z~N(0,1) (4)对给定的《=0.05确定临界值。因为是双侧备择假设所以查表时要注意。因概率表 是按单侧排列的,所以应查1-0.05/2=0.975的值,查得临界值Z-a2=1.96。 (⑤)检验准则。12≤1.96,接受,反之,拒绝 (6)决策:因Z=1.67<1.96:落在了接受域,因此认为今年7岁男孩平均身高与历年 7岁男孩平均身高无显著差异,即不能拒绝零假设。 【例73】一个生产宇航飞行器的工厂需要经常购置一种耐高温的零件,要求抗热的平 均温度是1250℃,在过去,供货者提供的产品都符合要求,并从大量的数据获知零件抗热 的标准差是150℃,在最近的一批进货中随机测试了100个零件,其平均的抗热为1200℃, 能否接受这批产品?工厂希望对实际产品符合要求而错误地加以拒绝的风险为0.05(即 a=0.05)。 解:检验的步暖如下: (1)建立假设。由于检验的目的是希望产品零件抗热的均值高于1250℃,而把低于 1250℃的加以拒绝,因此是一个单侧的假设检验问题。 H。:4≥1250C H1:4<1250 (2)这个检验中适当的检验统计量是: 6
6 策的规则,但显著性水平的规定可以先后灵活一些。 7.2 总体均值的假设检验 7.2.1 Z-检验 1.当总体分布为正态分布,总体标准差s 为已知时,检验原假设 0 0 H : m = m 。当 H0 成立时,由于总体 2 ~ 0 X N(m ,s ) ;所以样本均值 2 ~ 0 X N(m ,s / n) 。从而统计量为: 0 / X Z n m s - = ~ N(0,1) (7-1) 即它服从标准正态分布,于是可用它来检验原假设。 [例 7-2]某市历年来对 7 岁男孩的统计资料表明,他们的身高服从均值为 1.32 米、标 准差为 0.12 米的正态分布。现从各个学校随机抽取 25 个 7 岁男学生,测得他们平均身高 1.36 米,若已知今年全市 7 岁男孩身高的标准差仍为 0.12 米,问与历年 7 岁男孩的身高相 比是否有显著差异(取a =0.05)。 解:从题意可知, X =1.36 米,m 0 =1. 32 米,s =0.12 米。 (1)建立假设:H0:m =1.32,H1:m ¹ 1.32 (2)确定统计量: 1.36 1.32 1.67 / 0.12 / 25 X Z n m s - - = = = (3)Z 的分布:Z~N(0,1) (4)对给定的a =0.05 确定临界值。因为是双侧备择假设所以查表时要注意。因概率表 是按单侧排列的,所以应查 1-0.05/2=0.975 的值,查得临界值Z1-a / 2 =1.96。 (5)检验准则。|Z|£ 1.96,接受 H0,反之,拒绝 H0。 (6)决策:因 Z=1.67<1.96;落在了接受域,因此认为今年 7 岁男孩平均身高与历年 7 岁男孩平均身高无显著差异,即不能拒绝零假设。 【例 7-3】一个生产宇航飞行器的工厂需要经常购置一种耐高温的零件,要求抗热的平 均温度是 1 250℃,在过去,供货者提供的产品都符合要求,并从大量的数据获知零件抗热 的标准差是 150℃,在最近的一批进货中随机测试了 100 个零件,其平均的抗热为 1 200℃, 能否接受这批产品?工厂希望对实际产品符合要求而错误地加以拒绝的风险为 0.05(即 a =0.05)。 解:检验的步骤如下: (1)建立假设。由于检验的目的是希望产品零件抗热的均值高于 1 250℃,而把低于 1 250℃的加以拒绝,因此是一个单侧的假设检验问题。 H 0 ﹕ m ≥1 250℃ H 1 ﹕ m <1 250℃ (2)这个检验中适当的检验统计量是:

Z=- Gln (3)根据工厂的要求,显若性水平a=0.05,在这里是指当4=1250时而被拒绝的概 率为a。 (4)根据单侧检验a=0.05时,Z统计量拒绝域的临界值为-Z=-Zs=-1.645。 (5)计算统计量的数值 Z=x-4=1200-1250=-3.3 150/,/100 因为Z<Z。0s拒绝H。,接受H1,表明这一批产品零件的抗高温性能低于1250℃ 而不符合要求,因此不能接受这批产品 2对来自两个正态总体的两个独立样本,已知样本容量、均值和总体方差分别为 ,元,0和m,元2,0,可用Z检验法检验零很设:4=山。 可以证明,若~N(4,/n),x2~N(4,o/m,),则 (-X)N4-4+至 n 所以,在品成立的前提下,有 Z= X-X -N(0,1) (7-2) [例7-4]由长期积累的资料知道,甲、乙两城市20岁男青年的体重都服从正态分布, 并且标准差分别为14.2公斤和10.5公斤,现从甲、乙两城市各随机抽取27名20岁男青年 则测得平均体重分别为65.4公斤和54.7公斤,问甲、乙两城市20岁男青年平均体重有无 显著差异(a=0.05)? 解:从题意可知,元=65.4公斤,0,=14.2公斤,2=54.7公斤,02=10.5公斤: %==27。 ()建立假设:H:4=凸,H:4≠凸 (②)确定统计量: Z=-元 65.4-54.7 =3.15 CLo 14.2210.52 V%2 27+27 (3)Z的分布:Z~N(0,1) (4④)对给定的α=0.05确定临界值。因为是双侧备择假设所以查表时要注意。因概率表 7
7 n x Z / 0 s - m = (3)根据工厂的要求,显著性水平a =0.05,在这里是指当m =1 250 时而被拒绝的概 率为a 。 (4)根据单侧检验a =0.05 时,Z 统计量拒绝域的临界值为 1 .645 - Z = -Z 0. 05 = - 。 (5)计算统计量的数值 3 .33 150 / 100 1200 1250 / 0 = - - = - = n x Z s m 因为Z < Z a=0. 05 拒绝 H 0 ,接受 H 1 ,表明这一批产品零件的抗高温性能低于 1 250℃ 而不符合要求,因此不能接受这批产品。 2.对来自两个正态总体的两个独立样本,已知样本容量、均值和总体方差分别为 2 1 1 1 n , X ,s 和 2 2 2 2 n , X ,s ,可用 Z 检验法检验零假设 H0:m1 = m2 。 可以证明,若 2 2 1 ~ 1 1 1 2 2 2 2 X N(m ,s / n ), X ~ N(m ,s / n ),则 2 2 1 2 1 2 1 2 1 2 (X X ) ~ N( , ) n n s s - m - m + 所以,在 H0成立的前提下,有 1 2 2 2 1 2 1 2 ~ (0,1) X X Z N n n s s - = + (7-2) [例 7-4]由长期积累的资料知道,甲、乙两城市 20 岁男青年的体重都服从正态分布, 并且标准差分别为 14.2 公斤和 10.5 公斤, 现从甲、 乙两城市各随机抽取 27 名 20 岁男青年, 则测得平均体重分别为 65.4 公斤和 54.7 公斤,问甲、乙两城市 20 岁男青年平均体重有无 显著差异(a = 0.05)? 解:从题意可知, 1 X = 65.4 公斤,s 1 =14.2 公斤,X 2 =54.7 公斤,s 2 =10.5 公斤; 1 2 n = n = 27 。 (I)建立假设:H0:m1 = m2 ,H1:m1 ¹ m2 (2)确定统计量: 1 2 2 2 2 2 1 2 1 2 65.4 54.7 14.2 10.5 27 27 X X Z n n s s - - = = = + + 3.15 (3)Z 的分布:Z~N(0,1) (4)对给定的a =0.05 确定临界值。因为是双侧备择假设所以查表时要注意。因概率表

是按单侧排列的,所以应查1-0.05/2=0.975的值,查得临界值Z2=1.96。 (5)检验准则。z引≤1.96,接受H,反之,拒绝L (6)决策:因2= 15>1.96,落在了拒绝域,因此拒绝零假设。认为甲、乙两城市20 岁男青年平均体重有显著差异。 7.2.2T-检验 使用Z检验法需要知道总体标准差。,而实际问题中常常不知道。,这时必须用样本 标准差s代替总体标准差。,因此便有如下的t检验 t检验法是使用服从t分布的统计量检验正态总体平均值的方法。 1.当正态总体标准差。未知时,检验零假设H:4=%·可以证明,在H成立的前 提下,有: X-6 1=sNn合m-) (7-3) ∑(X-)月 (中,样本标准差S= (例7-5)某制药厂试制某种安定神经的新药,给10个病人试服,结果各病人增加睡 眠量如表7-2所示。 表7-2 病人服用新药增加睡眠量表 病人号码12345678910 增加睡眠(小时)0.7-1.1-0.21.20.13.43.70.81.82.0 试判断这种新药对病人有无安定神经的功效(α=0.05)。 解, (1)建立假设:4≤0(没有功效)。 H:4>0(有功效)(单侧备择假设) (②)计算统计量: ∑ ∑(X,-)2 灭= -=1.24s=1回 -=1.45 n 1.24-0 1= S1n-11.45/W10-1 =2.57 (3)确定统计量分布。本例中,1~1。 (4)对于给定的显著性水平0.05,查自由度为9的t分布表,单侧临界值为1.833 (5)建立检验规贝 t≤1.833,接受, 香则 拒绝 (6)结论。因为本例t=2.57>1.833,所以,拒绝H,即,认为这种新药对病人有安 定神经的功效。 8
8 是按单侧排列的,所以应查 1-0.05/2=0.975 的值,查得临界值Z1-a / 2 =1.96。 (5)检验准则。|Z|£ 1.96,接受 H0,反之,拒绝 H0。 (6)决策:因 Z=3.15>1.96,落在了拒绝域,因此拒绝零假设。认为甲、乙两城市 20 岁男青年平均体重有显著差异。 7.2.2 T-检验 使用 Z 检验法需要知道总体标准差s ,而实际问题中常常不知道s ,这时必须用样本 标准差 s 代替总体标准差s ,因此便有如下的 t 检验。 t 检验法是使用服从 t 分布的统计量检验正态总体平均值的方法。 1.当正态总体标准差s 未知时,检验零假设 H0:m = m0 。可以证明,在 H0 成立的前 提下,有: 0 ~ ( 1) / 1 X t t n S n - m = - - (7-3) (其中,样本标准差 2 1 ( ) n i i X X S n = - = Â ) 〔例 7-5〕某制药厂试制某种安定神经的新药,给 10 个病人试服,结果各病人增加睡 眠量如表 7-2 所示。 表 7-2 病人服用新药增加睡眠量表 病 人 号 码 1 2 3 4 5 6 7 8 9 10 增加睡眠(小时) 0.7 -1.1 -0.2 1.2 0.1 3.4 3.7 0.8 1.8 2.0 试判断这种新药对病人有无安定神经的功效(a =0.05)。 解: (1)建立假设 H0:m £ 0(没有功效)。 H1:m ﹥0 (有功效)(单侧备择假设) (2)计算统计量: 1 n i i X X n = = Â =1.24 2 1 ( ) n i i X X s n = - = Â =1.45 0 1.24 0 / 1 1.45/ 10 1 X t S n - m - = = - - =2.57 (3)确定统计量分布。本例中, ~ 9 t t 。 (4)对于给定的显著性水平 0.05,查自由度为 9 的 t 分布表,单侧临界值为 1.833 (5)建立检验规则。|t|£ 1.833,接受 H0,否则,拒绝 H0。 (6)结论。因为本例 t=2.57﹥1.833,所以,拒绝 H0,即,认为这种新药对病人有安 定神经的功效

2若两个正态总体的标准差。未知,但知道其值相等,可用t检验来检验零假设,: 4=凸·当品成立时,可证明统计量: 元- 2(x-x,+2x-,P 11 n+22-2 nn2 (7-4) 元-灭, 1 ~1-2 等 (例7-6)某工业管理局在体制改革前后,分别调查了10个和12个企业的劳动生产率 情况,得知改革前后平均劳动生产率(元/人)为X,=2089、X2=2450,劳动生产率的 方差分别为5=7689:s=6850。又知体制改革前、后企业劳动生产率的标准差相等.问: 在显著性水平0.05下,改革前、后平均劳动生产率有无显著差异? 解 (1)建立假设:4=山(没有差别)。 h:4山<山(有差别)(左单侧备择假设) (2)计算统计量: 元-灭2 2089-2450 =-9.45 + 10×7689+12×6850,1+L 10+12-2 12+10 (3)确定统计量分布。本例中,1~10。 (4)对于给定的显著性水平0.05,查自由度为20的t分布表,左单侧临界值为-1.725 (5)建立检验规则。t小于-1.725,拒绝,否则,接受。 (6)结论。因为本例t=9.45<-1.725,所以,拒绝,即,在显著性水平0.05下, 改革前、后平均劳动生产率有显著差异,改革后的劳动生产率高于改革前的劳动生产率。 以上是对总体均值进行检验的Z检验法、t检验法。它们分别应用于不同前提条件下的 均值显著性检验,决不能混用。为了能更直观地掌握其使用前提和使用方法,我们总结出了 表式如表7-3所示。 表7-3均值检验表 条件 统计量及其分布 拒绝域 9
9 2.若两个正态总体的标准差s 未知,但知道其值相等,可用 t 检验来检验零假设 H0: m1 = m2 。当 H0成立时,可证明统计量: 1 2 1 2 2 2 1 1 2 2 1 1 1 2 1 2 1 2 2 2 2 1 1 2 2 1 2 1 2 ( ) ( ) 1 1 ( ) 2 ~ 1 1 ( ) 2 n n i i i i n n X X t X X X X n n n n X X t n s n s n n n n + = = - - = - + - + + - - = + + + - Â Â (7-4) 〔例 7-6〕某工业管理局在体制改革前后,分别调查了 l0 个和 12 个企业的劳动生产率 情况,得知改革前后平均劳动生产率(元/人)为 X 1 =2 089、 X 2 =2 450,劳动生产率的 方差分别为 2 1s =7 689; 2 2 s =6 850。又知体制改革前、后企业劳动生产率的标准差相等. 问: 在显著性水平 0.05 下,改革前、后平均劳动生产率有无显著差异? 解: (1)建立假设 H0:m1 = m2 (没有差别)。 H1:m1 p m 2 (有差别)(左单侧备择假设) (2)计算统计量: 1 2 2 2 1 1 2 2 1 2 1 2 2089 2450 1 1 10 7689 12 6850 1 1 ( ) ( ) 2 10 12 2 12 10 X X t n s n s n n n n - - = = + ¥ + ¥ + + + - + - =-9.45 (3)确定统计量分布。本例中, ~ 20 t t 。 (4) 对于给定的显著性水平 0.05, 查自由度为 20 的 t 分布表, 左单侧临界值为-1.725 (5)建立检验规则。t 小于-1.725, 拒绝 H0,否则,接受 H0。 (6)结论。因为本例 t=-9.45<-1.725,所以,拒绝 H0,即,在显著性水平 0.05 下, 改革前、后平均劳动生产率有显著差异,改革后的劳动生产率高于改革前的劳动生产率。 以上是对总体均值进行检验的 Z 检验法、t 检验法。它们分别应用于不同前提条件下的 均值显著性检验,决不能混用。为了能更直观地掌握其使用前提和使用方法,我们总结出了 表式如表 7-3 所示。 表 7-3 均值检验表 方 法 条件 H0 H1 统计量及其分布 拒绝域
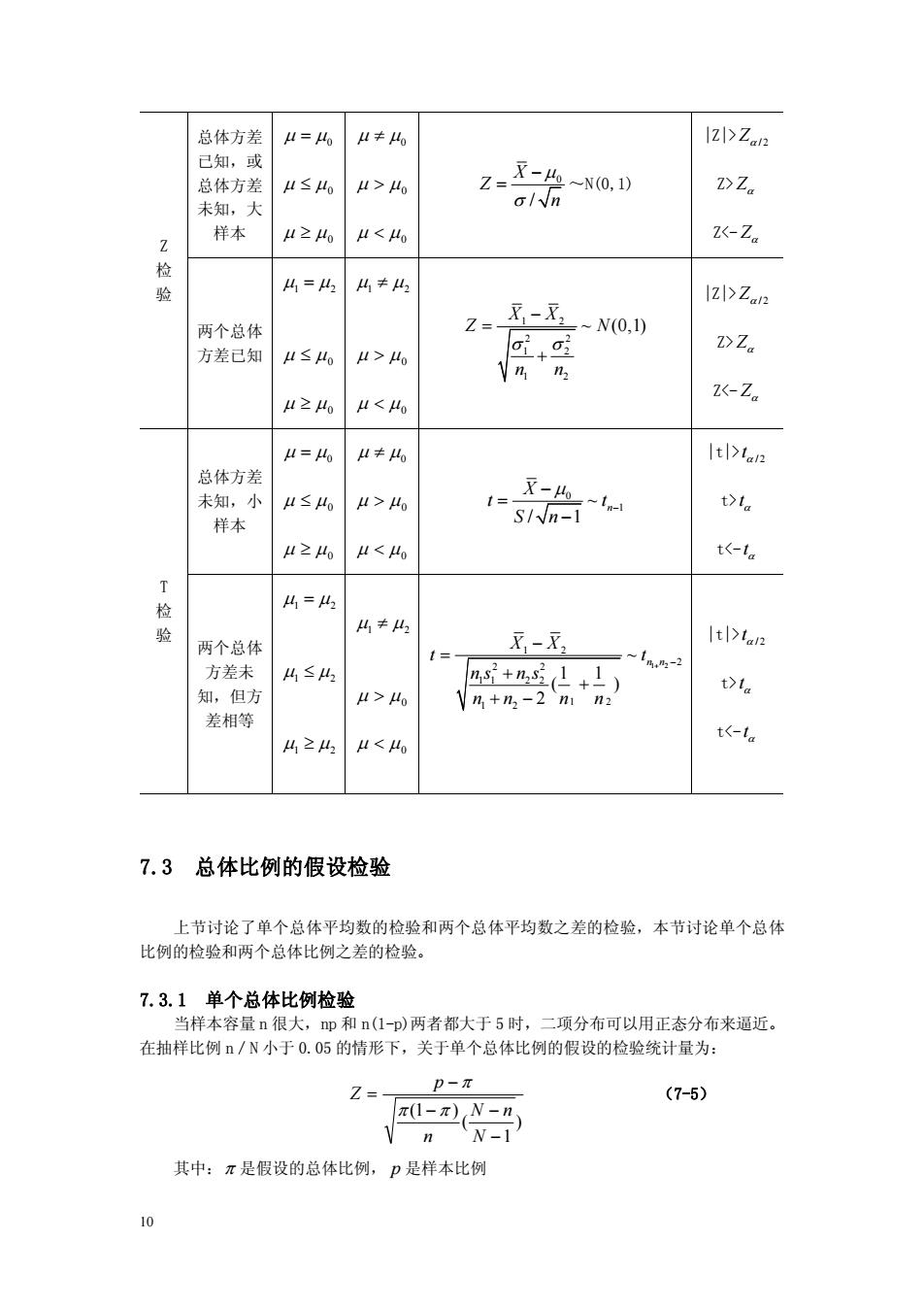
总休方弟 =% IZI>Zw 或 总体方 I≤ I>4 DZ /n 卡知, 样木 4Za 两个总体 ~N(0,1) D>Z 方差已 H>40 μ≥4 Z-Zg =Mo I≠ tton 总体方美 未知, μ≤A > 1= X-4 S/- t> 样本 12 f= 方差未 4≤ 知, 但方 μ>4o + 差相等 424 4<4 t<-la 7.3总体比例的假设检验 上节讨论了单个总体平均数的检验和两个总体平均数之差的检验,本节讨论单个总体 比例的检验和两个总体比例之差的检验。 7.3.1单个总体比例检验 当样本容量n很大,p和n(1-p)两者都大于5时,二项分布可以用正态分布来逼近, 在抽样比例n/N小于0.05的情形下,关于单个总体比例的假设的检验统计量为: 2= p-I (7-5) π1-π)N-n V n W-1 其中:π是假设的总体比例,P是样本比例
10 总体方差 已知,或 总体方差 未知,大 样本 m = m0 m £ m 0 m ³ m 0 m ¹ m0 m > m 0 m Za / 2 Z> Za Z m 0 m Za / 2 Z> Za Z m 0 m / 2 ta t> ta t m 0 m / 2 ta t> ta t<- ta 7.3 总体比例的假设检验 上节讨论了单个总体平均数的检验和两个总体平均数之差的检验,本节讨论单个总体 比例的检验和两个总体比例之差的检验。 7.3.1 单个总体比例检验 当样本容量 n 很大,np 和 n(1-p)两者都大于 5 时,二项分布可以用正态分布来逼近。 在抽样比例 n/N 小于 0.05 的情形下,关于单个总体比例的假设的检验统计量为: ) 1 ( (1 ) - - - - = N N n n p Z p p p (7-5) 其中:p 是假设的总体比例, p 是样本比例