
,令g2 shpplica 第十一章均勻设计及其应用 注:资料来源于中国数学会均匀设计分会
注:资料来源于中国数学会均匀设计分会

前 沐浴在改革开发的阳光下,神州大地生机盎然, 新生事物层出不穷。在科教兴国建设社会主义的 过程中,人们所熟悉的那些传统的试验设计方法 (如对比试验设计、全面试验设计、正交试验设 计等),已不能充分满足快节奏高效率的要求。 新时期呼唤新思维,新方法。 中国科学家巧妙的将“数轮方法”和“笼计武酸 孩计”相结合,发明了一种全新的试验设计方法 这就是均力孩计信。 均匀设计法诞生于1978年。由中国著名数学 家方开泰教授和王元院士合作共同发明
沐浴在改革开发的阳光下,神州大地生机盎然, 新生事物层出不穷。在科教兴国建设社会主义的 过程中,人们所熟悉的那些传统的试验设计方法 (如对比试验设计、全面试验设计、正交试验设 计等),已不能充分满足快节奏高效率的要求。 新时期呼唤新思维,新方法。 中国科学家巧妙的将“数论方法”和“统计试验 设计”相结合,发明了一种全新的试验设计方法 ,这就是均匀设计法。 均匀设计法诞生于1978年。由中国著名数学 家方开泰教授和王元院士合作共同发明。 前 言

正交设计可使试验点“均匀分散、整齐可 比”,为保证“整齐可比性”,使试验设计的 均匀性受到了一定限制,使试验点的代表性还 不够强,试验次数不能充分地少。 均匀设计是另一种部分实施的试验设计方 法。它可以用较少的试验次数,安排多因素、 多水平的析因试验,是在均匀性的度量下最好 的析因试验设计方法。它可以使试验,点在试验 范围内充分地均匀分散,不仅可大大减少试验 点,而且仍能得到反映试验体系主要特征的试 验结果
正交设计可使试验点“均匀分散、整齐可 比”,为保证“整齐可比性”,使试验设计的 均匀性受到了一定限制,使试验点的代表性还 不够强,试验次数不能充分地少。 均匀设计是另一种部分实施的试验设计方 法。它可以用较少的试验次数,安排多因素、 多水平的析因试 验,是在均匀性的度量下最好 的析因试验设计方法。它可以使试验点在试验 范围内充分地均匀分散,不仅可大大减少试验 点,而且仍能得到反映试验体系主要特征的试 验结果

购勾设计房鞋

下面通过制药工业中的一个实例来说 明均匀试验设计方法。 例1.1:阿魏骇的制备 阿魏酸是某些药品的主要成分,在制 备过程中,我们想提高阿魏酸产量。 根据试验目的,确定以阿魏酸产量作为试验 指标Y
下面通过制药工业中的一个实例来说 明均匀试验设计方法。 例1.1 :阿魏酸的制备 根据试验目的,确定以阿魏酸产量作为试验 指标Y。 阿魏酸是某些药品的主要成分,在制 备过程中,我们想提高阿魏酸产量

经过资料查阅,分析研究,选出影响阿魏酸产量的试 验因素,确定试验因素水平为: 原料配比:1.0-3.4 吡啶总量:10-28 反应时间:0.5-3.5 确定每个因素相应的水平数为7。 如何安排试验? 全面交叉试验要N=73=343次,太多了。 建议使用均匀设计。查阅均匀设计表。 “方开泰,均匀设计与均匀设计表,科学出版社 (1994) 之附表1 也可以浏览如下网页: 网络地址:http:/www.math.hkbu.edu.hk/UniformDesing
全面交叉试验要N=73=343次,太多了。 建议使用均匀设计。查阅均匀设计表。 经过资料查阅,分析研究,选出影响阿魏酸产量的试 验因素,确定试验因素水平为: 原料配比:1.0-3.4 吡啶总量:10-28 反应时间:0.5-3.5 确定每个因素相应的水平数为7。 如何安排试验? “方开泰,均匀设计与均匀设计表,科学出版社 (1994)” 之附表 1 网络地址:http://www.math.hkbu.edu.hk/UniformDesing 也可以浏览如下网页:
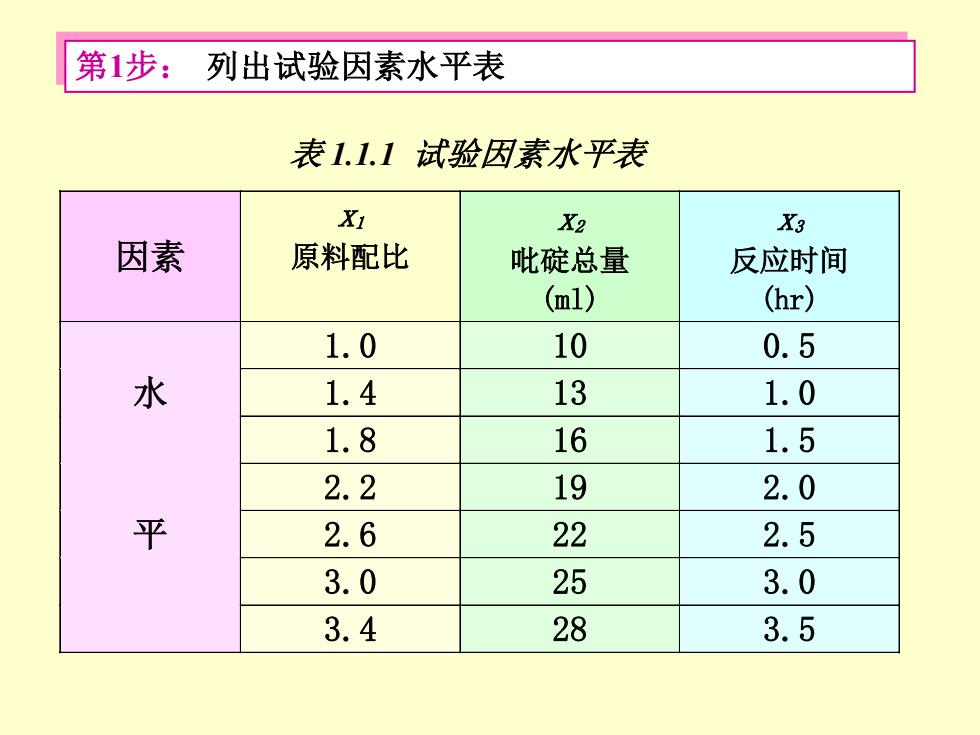
第1步:列出试验因素水平表 表1.1.1试验因素水平表 X1 Xa Xg 因素 原料配比 吡碇总量 反应时间 (ml) (hr) 1.0 10 0.5 水 1.4 13 1.0 1.8 16 1.5 2.2 19 2.0 平 2.6 22 2.5 3.0 25 3.0 3.4 28 3.5
因素 x1 原料配比 x2 吡碇总量 (ml) x3 反应时间 (hr) 1.0 10 0.5 水 1.4 13 1.0 1.8 16 1.5 2.2 19 2.0 平 2.6 22 2.5 3.0 25 3.0 3.4 28 3.5 第1步: 列出试验因素水平表 表 1.1.1 试验因素水平表

第2步:选择相应的均匀设计表 均匀设计表格式见下,其含义为: 均匀设计 因素数 U(q) 试验总次数 因素水平数
第2步: 选择相应的均匀设计表 均匀设计表格式见下,其含义为: Un (qs ) 均匀设计 试验总次数 因素水平数 因素数

例如: 表1.1.3: Ug(94) 表1.1.2: U7(74) No 1 2 3 4 No. 1 2 3 4 1 1 2 1 3 1 1 2 3 6 2 2 5 4 5 2 2 4 6 5 3 3 9 8 7 3 3 6 2 4 4 4 3 6 9 4 4 1 5 3 5 5 7 1 5 5 3 1 2 6 6 2 6 6 6 5 4 1 7 7 9 4 7 7 7 1 7 8 8 6 3 8 9 9 8 5 2
例如 : ( 7 ) 4 U7 No. 1 2 3 4 1 1 2 3 6 2 2 4 6 5 3 3 6 2 4 4 4 1 5 3 5 5 3 1 2 6 6 5 4 1 7 7 7 7 7 (9 ) 4 U9 No. 1 2 3 4 1 1 2 1 3 2 2 5 4 5 3 3 9 8 7 4 4 3 6 9 5 5 4 7 1 6 6 7 2 6 7 7 1 9 4 8 8 6 3 8 9 9 8 5 2 表 1.1.2: 表 1.1.3:
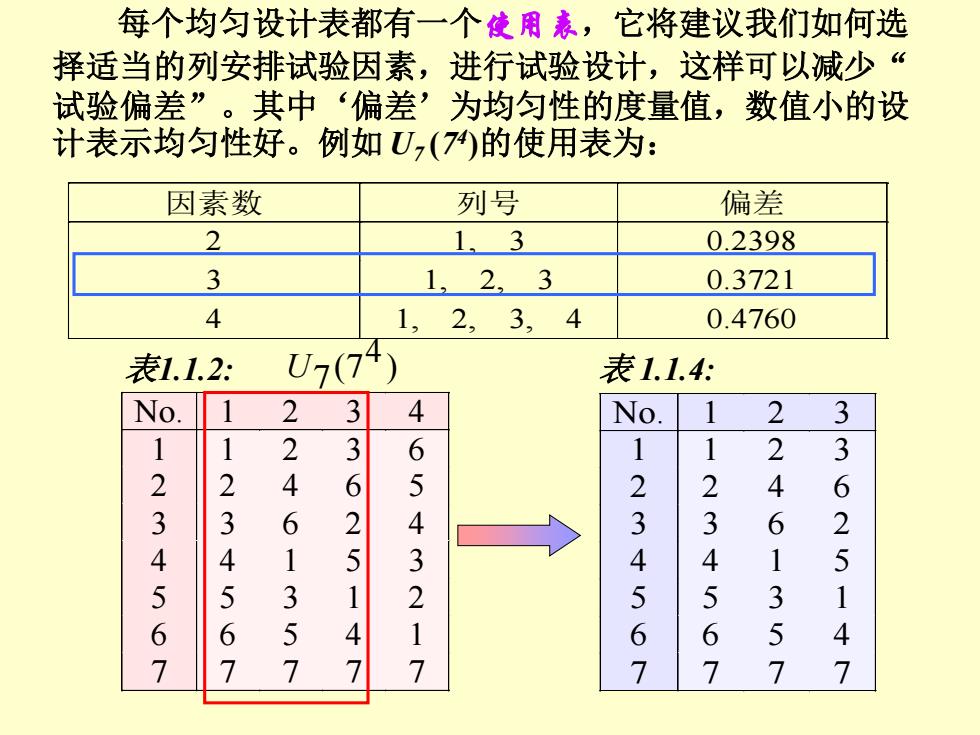
每个均匀设计表都有一个使用表,它将建议我们如何选 择适当的列安排试验因素,进行试验设计,这样可以减少“ 试验偏差”。其中‘偏差’为均匀性的度量值,数值小的设 计表示均匀性好。例如U,(7的使用表为: 因素数 列号 偏差 2 1.3 0.2398 3 1,2,3 0.3721 4 1,2,3,4 0.4760 表1.1.2 U7(74) 表1.1.4 No. 1 2 3 4 No. 1 2 3 1 1 2 3 6 1 2 3 2 2 4 6 5 2 2 4 6 3 3 6 2 4 3 6 2 4 1 5 4 4 1 5 5 5 3 1 2 5 5 3 1 6 5 4 1 6 6 5 4 7 7 7 7
每个均匀设计表都有一个使用表,它将建议我们如何选 择适当的列安排试验因素,进行试验设计,这样可以减少“ 试验偏差”。其中‘偏差’为均匀性的度量值,数值小的设 计表示均匀性好。例如 U7 (7 4 )的使用表为: 因素数 列号 偏差 2 1, 3 0.2398 3 1, 2, 3 0.3721 4 1, 2, 3, 4 0.4760 No. 1 2 3 4 1 1 2 3 6 2 2 4 6 5 3 3 6 2 4 4 4 1 5 3 5 5 3 1 2 6 6 5 4 1 7 7 7 7 7 No. 1 2 3 1 1 2 3 2 2 4 6 3 3 6 2 4 4 1 5 5 5 3 1 6 6 5 4 7 7 7 7 ) 4 (7 表1.1.2: U7 表 1.1.4: