
第10章相关与回归分析 学习目标 1、了解相关关系的概念及种类: 2、掌握相关系数的计算方法和相关系数的取值含义: 3、掌握一元线性回归直线方程的建立方法、回归方程的显著性检验和回归预测的方法: 4、了解多元线性回归直线方程的建立方法。 基本概念 函数关系相关关系相关表相关图相关系数最小二乘法一元线性回归多 元线性回归 10.1相关分析概述 10.1.1函数关系与相关关系 客观世界中的许多现象都存在者有机的联系,而且这些联系可以通过一定的数最关系反 映出来。例如,家庭收入与消费之间的关系、产品产量与单位成本之间的关系、广告费与商 品销售额之间的关系等等。这些变量之间就其关系的变化来说, 一般可分为两大类型:一是 函数关系,二是相关关系。 1.函数关系 当一个或几个变量取一定的值时,另一个变量有确定的值与之相对应,我们称这种关系 为确定性的承函数关系。例如,某种产品的总成木S与该产品的产量以及该产品的单位成木日 之间的关系可用SP9表达,这就是一种函数关系。通常把作为影响因素的变量称为自变量 把 生相应变 的量称为因变量。在本例中,S是因变量,P与Q则是自变量 2.相关关系 一个或几个相互联系的变量取一定数值时,与之相对应的另一变量的值虽然不确定 但它仍按某种规律在一定的范围内变化,变量间的这种相互关系,称为具有不确定性的相关 关系。例如,商品销售额与商品流通费之间的关系。一般说米,商品销售额增加,商品流通 费便要相应增加: 反 ,就要相应减少。但是商 销售额与商品流通费 之间不存在 的确定性关系。因为商品流通费的支付不仅与商品销售数量有关,而且与商品性质、运价、 运输里程、运输方式、广告宣传、经营管理等诸多因素有关。在商品销售额相同的情况下各 企业支付的流通费用有高有低。 10.1.2相关关系的种类 现象之间的相互关系是很复杂的,它们以不同的方向、不同的程度相互作用,表现为各 种形态,我们可以按不同的标准加以划分。 1.按相关关系涉及的变量(因素)多少来划分,可分为单相关和复相关 单相关是指一个自变量与一个因变量的依存关系。复相关是指一个因变量与两个或两个 以上自变量之间的依存关系。例如,某种商品的需求量与其价格水平之间呈单相关:而某种 商品的需求最与其价格水平 职工 收入 其他同类商品的价格之间呈复相关 2.按相关关系的表现形态来划分,可分为线性相关和非线性相关
1 第 10 章 相关与回归分析 学习目标 1、了解相关关系的概念及种类; 2、掌握相关系数的计算方法和相关系数的取值含义; 3、掌握一元线性回归直线方程的建立方法、回归方程的显著性检验和回归预测的方法; 4、了解多元线性回归直线方程的建立方法。 基本概念 函数关系 相关关系 相关表 相关图 相关系数 最小二乘法 一元线性回归 多 元线性回归 10.1 相关分析概述 10.1.1 函数关系与相关关系 客观世界中的许多现象都存在着有机的联系, 而且这些联系可以通过一定的数量关系反 映出来。例如,家庭收入与消费之间的关系、产品产量与单位成本之间的关系、广告费与商 品销售额之间的关系等等。这些变量之间就其关系的变化来说,一般可分为两大类型:一是 函数关系,二是相关关系。 1.函数关系 当一个或几个变量取一定的值时,另一个变量有确定的值与之相对应,我们称这种关系 为确定性的函数关系。例如,某种产品的总成本 S 与该产品的产量以及该产品的单位成本 P 之间的关系可用 S=PQ 表达,这就是一种函数关系。 通常把作为影响因素的变量称为自变量, 把发生相应变化的量称为因变量。在本例中,S 是因变量,P 与 Q 则是自变量。 2.相关关系 当一个或几个相互联系的变量取一定数值时,与之相对应的另一变量的值虽然不确定, 但它仍按某种规律在一定的范围内变化, 变量间的这种相互关系, 称为具有不确定性的相关 关系。例如,商品销售额与商品流通费之间的关系。一般说来,商品销售额增加,商品流通 费便要相应增加;反之,就要相应减少。但是商品销售额与商品流通费之间不存在一一对应 的确定性关系。因为商品流通费的支付不仅与商品销售数量有关,而且与商品性质、运价、 运输里程、运输方式、广告宣传、经营管理等诸多因素有关。在商品销售额相同的情况下各 企业支付的流通费用有高有低。 10.1.2 相关关系的种类 现象之间的相互关系是很复杂的,它们以不同的方向、不同的程度相互作用,表现为各 种形态,我们可以按不同的标准加以划分。 1.按相关关系涉及的变量(因素)多少来划分,可分为单相关和复相关 单相关是指一个自变量与一个因变量的依存关系。 复相关是指一个因变量与两个或两个 以上自变量之间的依存关系。例如,某种商品的需求量与其价格水平之间呈单相关;而某种 商品的需求量与其价格水平、职工收入水平、其他同类商品的价格之间呈复相关。 2.按相关关系的表现形态来划分,可分为线性相关和非线性相关

当自变量数值发生变动,.因变量数值随若发生大致均等的变动(增加或减少),从图形上 看,其观察点的分布近似地表现为一条直线形式,称为线性相关。当自变量数值发生变动, 变量数 着也发生变动,但不是均等的变动,从图形上看,其观察点的分布近似地表现 为各种不同的曲线形式,如抛物线、双曲线等,称为非线性相关。 3按变量之间相互关系的方向,分为正相关和负相关 当自变量的数值增加,因变量的数值也随之相应的增加,即相关的变量同一方向变化, 称为正相关。例如施肥量增加,亩产量也增加,企业固定资产价值增加,产品产量也随之增 加等,这种关系就是正相关。自变量数值增加时,因变量数值随之减少,即相关的变量反方 向变化,称为负相关。例如劳动生产率提高,单位产品的消耗时间就会随之减少等,这种关 系就是负相关。 4按变量之间相关的程度划分,可分为完全相关、不相关(也称零相关)和不完全相关 因变量数值完全随自变量数值变动而变动,这时相关关系实际上就转化为函数关系,利 为完全相关。变量之间的变动完全不存在任何依存关系时,称为不相关。变量之间关系介于 完全相关 不完全相关之间,称为不完全相关。一般的相关现象都是指这种不完全相关,这 是相关分析的主要内容。 10.1.3相关分析的主要内容 限低现象州视李美系切程度的厨究相去分析。麦量的相张性想高,有的相关号 分析我们可以得到现象间相互关系的密切程度和变化规律。 相关分析的主要内容有: 1.确定现象之间有无相关关系及相关关系的表现形式。主要通过定性分析判断和相关 图、相关表观察得出结论。这是相关分析的出发点。 2.确定相关关系的表现形式。若存在相关关系,就需进一步确定相互关系的表现形式 例如,是线性相关还是非线性相关,这时相关分析的主要内容 3确定相关关系的密切程度和方向。通过相关分析 可以判定现象之间相关关系的密 切程度和方向。例如,变量之间是完全相关、不完全相关还是完全不相关。 相关分析的内容很多,本章仅介绍直线相关的最主要、最基本内容。 10.2相关关系的测定 要进行相关分析首先要判断现象之间有没有相关关系和具有什么样的相关关系。我们 般是先对现象之间的关系作直观判断,然后再进行相应的定量分析。直观判断的方法主要有 两种:一是运用理论知识、专业知识及实际经验对现象之间存在的关系作定性的判断:二是 利用相关表和相关图对现象之间存在的相关关系的方向、形式及紧密程度作出大致判断。定 量分析则主要是计算相关系数 10.2.1客观现象之间的定性分析 根据一定的社会经济理论与实践经验的总结,对社会经济现象进行定性分析,以判断它 们之间是否具有相关关系以及相关关系的种类。只有在定性分析的基础上,才能从数量上测 定现象之间的相关关系。这是判断相关关系的一种重要的方法,也是相关分析的重要的前提, 10.2.2利用相关图表进行判断 判断现象之间的相关关系,一般是先做定性分析,然后再做定量分折。如果定性分析确 有相关关系.进一步编制相关图与相关表、可以判断现象之间大致呈现何种关系形式,以此 2
2 当自变量数值发生变动,因变量数值随着发生大致均等的变动(增加或减少),从图形上 看,其观察点的分布近似地表现为一条直线形式,称为线性相关。当自变量数值发生变动, 因变量数值随着也发生变动,但不是均等的变动,从图形上看,其观察点的分布近似地表现 为各种不同的曲线形式,如抛物线、双曲线等,称为非线性相关。 3.按变量之间相互关系的方向,分为正相关和负相关 当自变量的数值增加,因变量的数值也随之相应的增加,即相关的变量同一方向变化, 称为正相关。例如施肥量增加,亩产量也增加,企业固定资产价值增加,产品产量也随之增 加等,这种关系就是正相关。自变量数值增加时,因变量数值随之减少,即相关的变量反方 向变化,称为负相关。例如劳动生产率提高,单位产品的消耗时间就会随之减少等,这种关 系就是负相关。 4.按变量之间相关的程度划分,可分为完全相关、不相关(也称零相关)和不完全相关 因变量数值完全随自变量数值变动而变动,这时相关关系实际上就转化为函数关系, 称 为完全相关。变量之间的变动完全不存在任何依存关系时,称为不相关。变量之间关系介于 完全相关与不完全相关之间,称为不完全相关。一般的相关现象都是指这种不完全相关,这 是相关分析的主要内容。 10.1.3 相关分析的主要内容 对现象间相关关系密切程度的研究,叫相关分析。变量间有的相关性很高,有的相关性 很低,通过相关分析我们可以得到现象间相互关系的密切程度和变化规律。 相关分析的主要内容有: 1.确定现象之间有无相关关系及相关关系的表现形式。主要通过定性分析判断和相关 图、相关表观察得出结论。这是相关分析的出发点。 2.确定相关关系的表现形式。若存在相关关系,就需进一步确定相互关系的表现形式。 例如,是线性相关还是非线性相关,这时相关分析的主要内容。 3.确定相关关系的密切程度和方向。通过相关分析,可以判定现象之间相关关系的密 切程度和方向。例如,变量之间是完全相关、不完全相关还是完全不相关。 相关分析的内容很多,本章仅介绍直线相关的最主要、最基本内容。 10.2 相关关系的测定 要进行相关分析首先要判断现象之间有没有相关关系和具有什么样的相关关系。 我们一 般是先对现象之间的关系作直观判断,然后再进行相应的定量分析。直观判断的方法主要有 两种:一是运用理论知识、专业知识及实际经验对现象之间存在的关系作定性的判断;二是 利用相关表和相关图对现象之间存在的相关关系的方向、形式及紧密程度作出大致判断。定 量分析则主要是计算相关系数。 10.2.1 客观现象之间的定性分析 根据一定的社会经济理论与实践经验的总结,对社会经济现象进行定性分析,以判断它 们之间是否具有相关关系以及相关关系的种类。只有在定性分析的基础上, 才能从数量上测 定现象之间的相关关系。 这是判断相关关系的一种重要的方法, 也是相关分析的重要的前提。 10.2.2 利用相关图表进行判断 判断现象之间的相关关系,一般是先做定性分析,然后再做定量分折。如果定性分析确 有相关关系.进一步编制相关图与相关表、可以判断现象之间大致呈现何种关系形式,以此
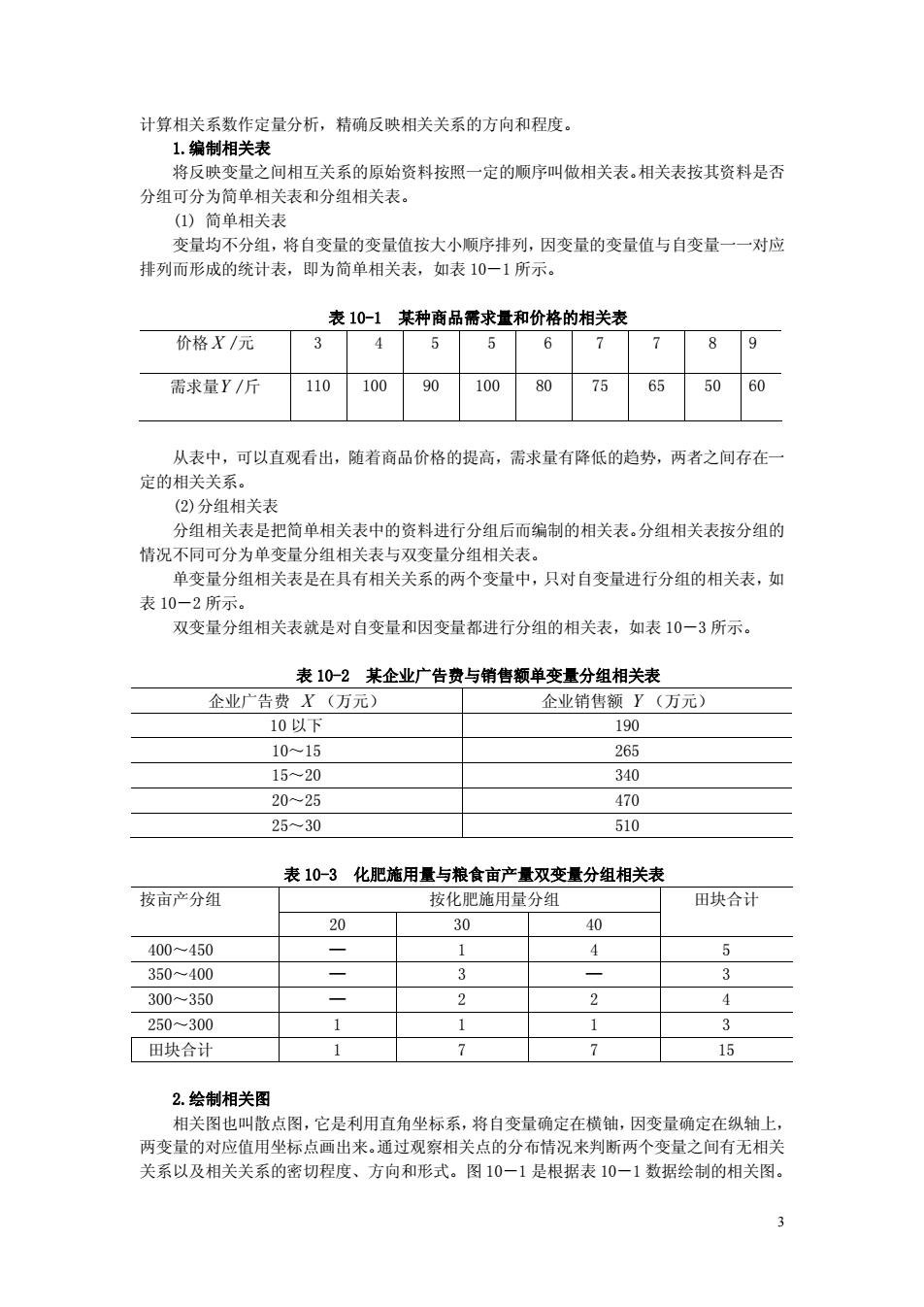
计算相关系数作定量分析,精确反映相关关系的方向和程度。 1.绵制相关表 将反映变量之间相互关系的原始资料按照一定的顺序叫做相关表。相关表按其资料是否 分组可分为简单相关表和分组相关表 (1)简单相关表 变量均不分组,将自变量的变量值按大小顺序排列,因变量的变量值与自变量一一对应 排列而形成的统计表,即为简单相关表,如表10一1所示。 表10-1某种商品需求量和价格的相关表 价格X/元 345567789 需求量Y/斤 110100901008075655060 从表中,可以直观看出,随着商品价格的提高,需求最有降低的趋势,两者之间存在 定的相关关系 (②)分组相关表 分组相关表是把简单相关表中的资料进行分组后而编制的相关表。分组相关表按分组的 情况不同可分为单变量分组相关表与双变量分组相关表。 单变量分组相关表是在具有相关关系的两个变量中,只对自变量进行分组的相关表,如 表10-2所示。 双变量分组相关表就是对自变量和因变量都进行分组的相关表,如表10一3所示。 表10-2某企业广告费与销售额单变量分组相关表 企业广告费X(万元) 企业销售额Y(万元) 10以下 190 10-15 265 15-20 340 2025 470 25-30 510 表10-3化肥施用量与粮食亩产量双变量分组相关表 按亩产分组 按化肥施用量分组 田块合计 20 30 40 400-450 350-400 3 300-350 2 4 250300 1 1 1 田块合计 1 7 7 15 2.绘制相关图 相关图也叫散点图,它是利用直角坐标系,将自变量确定在横铀,因变量确定在纵轴上, 两变量的对应值用坐标点画出来。通过观察相关点的分布情况来判断两个变量之间有无相关 关系以及相关关系的密切程度、方向和形式。图10一1是根据表10一1数据绘制的相关图 3
3 计算相关系数作定量分析,精确反映相关关系的方向和程度。 1.编制相关表 将反映变量之间相互关系的原始资料按照一定的顺序叫做相关表。 相关表按其资料是否 分组可分为简单相关表和分组相关表。 (1) 简单相关表 变量均不分组,将自变量的变量值按大小顺序排列, 因变量的变量值与自变量一一对应 排列而形成的统计表,即为简单相关表,如表 10-1 所示。 表 10-1 某种商品需求量和价格的相关表 价格 X /元 3 4 5 5 6 7 7 8 9 需求量Y /斤 110 100 90 100 80 75 65 50 60 从表中,可以直观看出,随着商品价格的提高,需求量有降低的趋势,两者之间存在一 定的相关关系。 (2)分组相关表 分组相关表是把简单相关表中的资料进行分组后而编制的相关表。 分组相关表按分组的 情况不同可分为单变量分组相关表与双变量分组相关表。 单变量分组相关表是在具有相关关系的两个变量中, 只对自变量进行分组的相关表, 如 表 10-2 所示。 双变量分组相关表就是对自变量和因变量都进行分组的相关表,如表 10-3 所示。 表 10-2 某企业广告费与销售额单变量分组相关表 企业广告费 X (万元) 企业销售额 Y (万元) 10 以下 190 10~15 265 15~20 340 20~25 470 25~30 510 表 10-3 化肥施用量与粮食亩产量双变量分组相关表 按亩产分组 按化肥施用量分组 20 30 40 田块合计 400~450 — 1 4 5 350~400 — 3 — 3 300~350 — 2 2 4 250~300 1 1 1 3 田块合计 1 7 7 15 2.绘制相关图 相关图也叫散点图, 它是利用直角坐标系, 将自变量确定在横铀, 因变量确定在纵轴上, 两变量的对应值用坐标点画出来。 通过观察相关点的分布情况来判断两个变量之间有无相关 关系以及相关关系的密切程度、方向和形式。图 10-1 是根据表 10-1 数据绘制的相关图
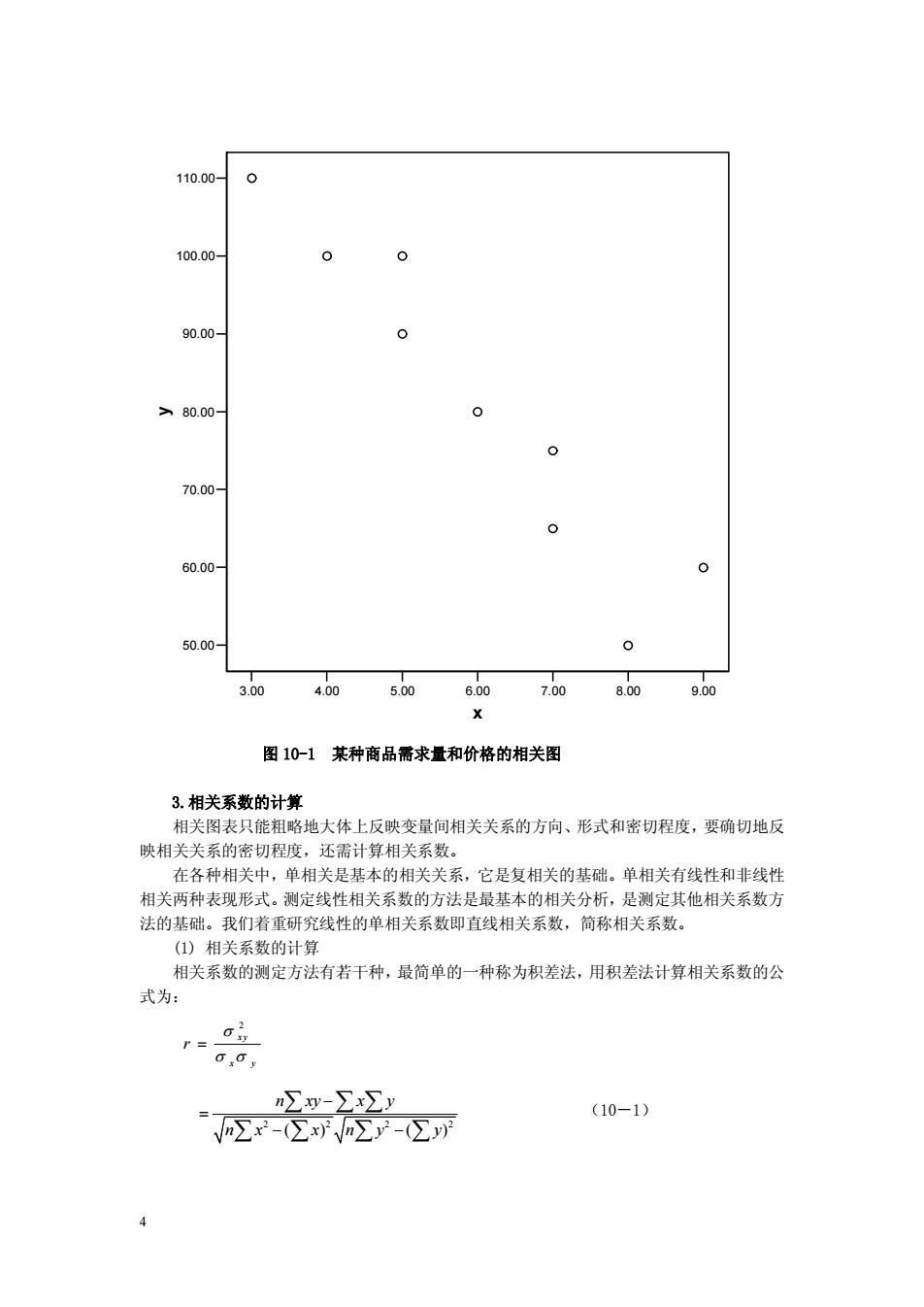
110.000 10.00 0 90.00 80.00 0 70.00- 60.00 0 50.00- 0 300400500600 70080900 图10-1某种商品需求量和价格的相关图 3.相关系断的计算 相关图表只能粗略地大体上反映变量间相关关系的方向、形式和密切程度,要确切地反 映相关关系的密切程度,还需计算相关系数。 在各种相关中,单相关是基本的相关关系,它是复相关的基础。单相关有线性和非线性 相关两种表现形式。测定线性相关系数的方法是最基本的相关分析,是测定其他相关系数方 法的基础。我们若重研究线性的单相关系数即直线相关系数,简称相关系数。 )相关系数的计算 相关系数的测定方法有若干种,最简单的一种称为积差法,用积差法计算相关系数的公 式为: r= n∑gy-∑x∑y (10-1) 2r-∑球-∑列
4 3.00 4.00 5.00 6.00 7.00 8.00 9.00 x 50.00 60.00 70.00 80.00 90.00 100.00 110.00 y 图 10-1 某种商品需求量和价格的相关图 3.相关系数的计算 相关图表只能粗略地大体上反映变量间相关关系的方向、形式和密切程度,要确切地反 映相关关系的密切程度,还需计算相关系数。 在各种相关中,单相关是基本的相关关系,它是复相关的基础。单相关有线性和非线性 相关两种表现形式。测定线性相关系数的方法是最基本的相关分析,是测定其他相关系数方 法的基础。我们着重研究线性的单相关系数即直线相关系数,简称相关系数。 (1) 相关系数的计算 相关系数的测定方法有若干种, 最简单的一种称为积差法,用积差法计算相关系数的公 式为: 2 x y x y r s s s = 2 2 2 2 ( ) ( ) n xy x y n x x n y y - = - - Â Â Â Â Â Â Â (10-1)

可-立 00 其中,O,=∑(x-xy-),称为灯的协方差: 0=√:∑(x-,是变量x的标准差: 0,=∑0-可,是变量y的标准差· 因此,相关系数可表现为如下形式: ∑(x-xy-) r=- ∑x-)'0y-) (10-2) (2)相关系数的取值范围和意义 通过数理证明,我们可以得到,相关系数的取值范围在一1和+1之间,即 -1≤r≤1。 当r=0时,表明x与y之间无线性相关关系。即x与y之间不相关或曲线相关。 变量x与y为完全线性相关,当r=1时,称为完全正相关:当r=-1 时,称为完全负相关 当00.8称为高度相关。 [例10-1]已知某种商品需求量和价格的数据,见表10-1,根据表中的资料,计算该商 品需求量和价格的相关系数 解:按相关系数公式计算 r ∑(x-xy-) ∑(x-)y-列 将表中数据代入公式 (x-6Mv-81.1) r=- =-0.948 ∑x-6∑0-81.F 由于r<0,且r=0.948,则说明该种商品的需求量和该种商品的价格是高度负相关 的 10.3回归分析 5
5 x y xy x y s s - = 其中, 1 ( )( ) xy n s = Â x - x y - y ,称为 xy 的协方差 ; 1 2 ( ) x n s = Â x - x , 是变量 x 的标准差 ; 1 2 ( ) y n s = Â y - y , 是变量 y 的标准差 。 因此,相关系数可表现为如下形式: 2 2 ( )( ) ( ) ( ) x x y y r x x y y - - = - - Â Â (10-2) (2)相关系数的取值范围和意义 通过数理证明,我们可以得到,相关系数的取值范围在-1 和+1 之间, 即 -1£ r £ 1 。 当 r = 0 时,表明 x 与 y 之间无线性相关关系。即 x 与 y 之间不相关或曲线相关。 当 r = ± 1 时,变量 x 与 y 为完全线性相关,当r = 1时,称为完全正相关;当r = - 1 时,称为完全负相关。 当0 0.8 称为高度相关。 [例 10-1]已知某种商品需求量和价格的数据,见表 10-1,根据表中的资料,计算该商 品需求量和价格的相关系数。 解:按相关系数公式计算 2 2 ( )( ) ( ) ( ) x x y y r x x y y - - = - - Â Â 将表中数据代入公式: 2 2 ( 6)( 81.1) 0.948 ( 6) ( 81.1) x y r x y - - = = - - - Â Â Â 由于r < 0 ,且 r = 0.948 ,则说明该种商品的需求量和该种商品的价格是高度负相关 的。 10.3 回归分析

回归这个统计术语,最早采用者是英国遗传学家高尔登。他把这种统计分析方法应用于 研究生物学的遗传问题,指出生物后代有回复或回归到其上代原有特性的倾向。高尔登的学 主皮尔逊继续研 ,将回归的 数学的方法联系起来,把代表现象之间一般数量关系的 直线或曲线称为回归直线或回归曲线。 相关分析中的相关系数可以从数量上说明变量之间相关关系的方向和密切程度。但它不 能反映一个变量发生一定数量的变化时.另一个变量会相应的发生多少变动。为了解决这个 问题,就必须采用回归分析的方法。回归分析是指对具有相关关系的变量,依据其关系形态 选择一个合适的数学模型,用来近似的表示变量之间数量平均变化关系的一种统计方法。回 归分析的内容很多,按分析变量的多少不同,可分为一元回归分析和多元回归分析:按分析 变量的表现形态不同,可分为线性回归分析与非线性回归分析等。本节只讨论一元线性回归 分析的理论与方法。 10.3.1一元线性回归模型的描述 元线性回归模型也称为简单直线回归模型,是分析两个变量x与y之间相互关系的数 学方程式。我们假定x为自变量,y为因变量,y值除了受自变量x的影响之外,还受其它 因素的影响:在构建回归模型时,应该包括随机误差£,x与y之间的关系可以用数学公 式表示: y=a+bx+g (10-3) 在实际研究问题时,为了便于对参数做出区间估计和假设检验,我们假定~N(0,σ)· 因此,我们可以用下式近似的描述x与y之间的关系: j=a+bx (10-4) 式中y为因变量的估计值:x为自变量的实际值:a,b为待定参数:公式(10-4)称 为变量y对x的一元线性回归模型。 a,b的几何意义是:a为直线方程的截距,b为直线的斜率。其经济意义是:a表示自 变量x为零时的因变量y的估计值:b表示当自变量x每增加一个单位时因变量y的平均变 化,b也称为y对x的回归系数。 10.3.2一元线性回归方程的拟合 元线性回归方程的建立,是对两个变量进行回归分析的第一步,下面我们不妨以某企 业广告费支出与销售额之间的关系问题为例来进行说明。资料如表10-4所示 我们可以在平面直角坐标系上画出广告费支出与销售额的散点图。见图10-2。 表10-4某企业广告费支出与销售额数据(单位:万元) 广告费x 67 4 5 39 销售额y 50587040603037 80
6 回归这个统计术语,最早采用者是英国遗传学家高尔登。他把这种统计分析方法应用于 研究生物学的遗传问题,指出生物后代有回复或回归到其上代原有特性的倾向。高尔登的学 生皮尔逊继续研究,将回归的概念和数学的方法联系起来,把代表现象之间一般数量关系的 直线或曲线称为回归直线或回归曲线。 相关分析中的相关系数可以从数量上说明变量之间相关关系的方向和密切程度。 但它不 能反映一个变量发生一定数量的变化时. 另一个变量会相应的发生多少变动。为了解决这个 问题, 就必须采用回归分析的方法。 回归分析是指对具有相关关系的变量, 依据其关系形态, 选择一个合适的数学模型,用来近似的表示变量之间数量平均变化关系的一种统计方法。回 归分析的内容很多,按分析变量的多少不同,可分为一元回归分析和多元回归分析;按分析 变量的表现形态不同, 可分为线性回归分析与非线性回归分析等。 本节只讨论一元线性回归 分析的理论与方法。 10.3.1 一元线性回归模型的描述 一元线性回归模型也称为简单直线回归模型, 是分析两个变量 x 与 y 之间相互关系的数 学方程式。我们假定 x 为自变量,y 为因变量,y 值除了受自变量 x 的影响之外,还受其它 因素的影响;在构建回归模型时,应该包括随机误差e ,x 与 y 之间的关系可以用数学公 式表示: y = a + bx + e (10-3) 在实际研究问题时, 为了便于对参数做出区间估计和假设检验, 我们假定 2 e ~ N(0,s ) 。 因此,我们可以用下式近似的描述 x 与 y 之间的关系: yˆ = a + b x (10-4) 式中 y ˆ 为因变量的估计值;x 为自变量的实际值;a ,b 为待定参数;公式(10-4)称 为变量 y 对 x 的一元线性回归模型。 a ,b 的几何意义是:a 为直线方程的截距,b 为直线的斜率。其经济意义是:a 表示自 变量 x 为零时的因变量 y 的估计值;b 表示当自变量 x 每增加一个单位时因变量 y 的平均变 化,b 也称为 y 对 x 的回归系数。 10.3.2 一元线性回归方程的拟合 一元线性回归方程的建立,是对两个变量进行回归分析的第一步, 下面我们不妨以某企 业广告费支出与销售额之间的关系问题为例来进行说明。资料如表 10-4 所示: 我们可以在平面直角坐标系上画出广告费支出与销售额的散点图。见图 10-2 。 表 10-4 某企业广告费支出与销售额数据(单位:万元) 广告费 x 6 7 8 4 5 2 3 9 销售额 y 50 58 70 40 60 30 37 80
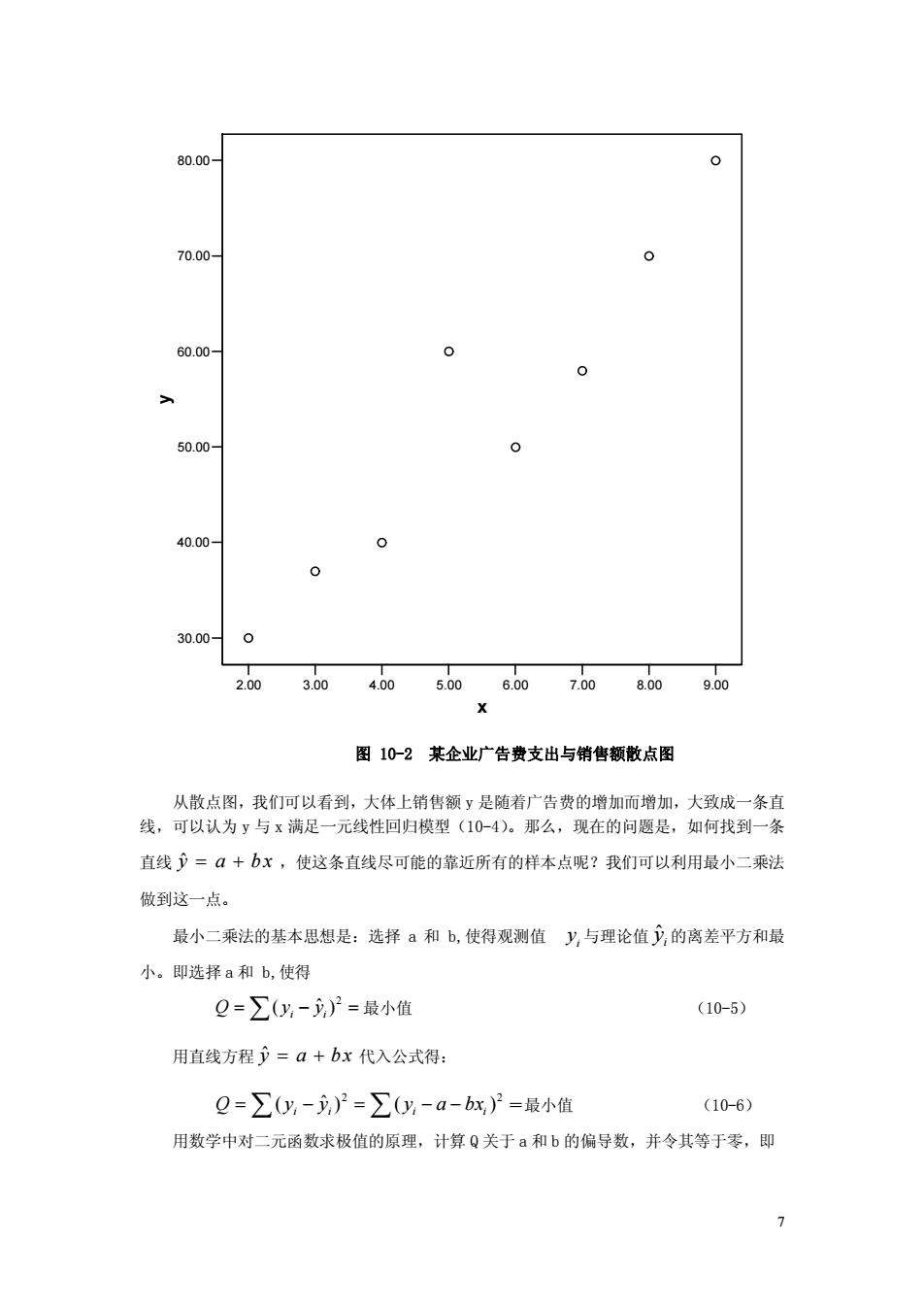
8000 70.00 0 60.00 50.00 40.00 0 0 30.000 2.00 3.00 4.00 5.00 6.00 7.008009.00 图10-2某企业广告费支出与销售额散点图 从散点图,我们可以看到,大体上销售额y是随者广告费的增加而增加,大致成一条直 线,可以认为y与x满足一元线性回归模型(10-4)。那么,现在的问题是,如何找到一条 直线=+bx,使这条直线尽可能的靠近所有的样本点呢?我们可以利用最小二乘法 做到这一点。 最小二乘法的基本思想是:选择a和b,使得观测值y与理论值少的离差平方和最 小。即选择a和b,使得 Q=∑y-)=最小值 (10-5) 用直线方程少=a+bx代入公式得: Q=∑0y-)》2=∑(y-a-bx)2=最小值 (10-6) 用数学中对二元函数求极值的原理,计算Q关于a和b的偏导数,并令其等于零,即 >
7 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 x 30.00 40.00 50.00 60.00 70.00 80.00 y 图 10-2 某企业广告费支出与销售额散点图 从散点图,我们可以看到,大体上销售额 y 是随着广告费的增加而增加,大致成一条直 线,可以认为 y 与 x 满足一元线性回归模型(10-4) 。那么,现在的问题是,如何找到一条 直线 yˆ = a + b x ,使这条直线尽可能的靠近所有的样本点呢?我们可以利用最小二乘法 做到这一点。 最小二乘法的基本思想是:选择 a 和 b,使得观测值 i y 与理论值 ˆ i y 的离差平方和最 小。即选择 a 和 b,使得 2 ( ˆ ) Q i i = Â y - y = 最小值 (10-5) 用直线方程 yˆ = a + bx 代入公式得: 2 2 ( ˆ ) ( ) Q i i i i = Â y - y = Â y - a - bx =最小值 (10-6) 用数学中对二元函数求极值的原理,计算 Q 关于 a 和 b 的偏导数,并令其等于零,即
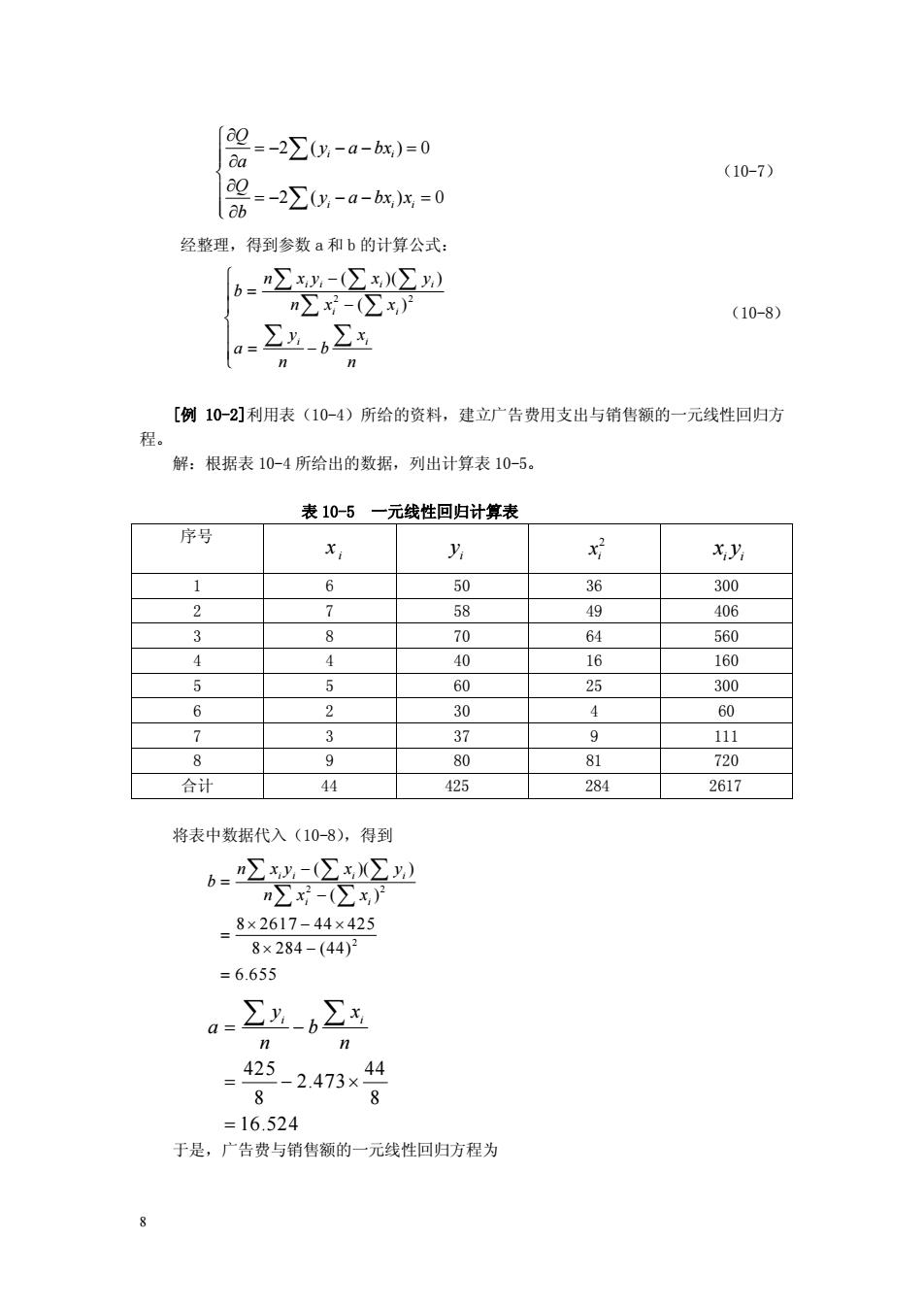
(10-7) 0-2∑0y-a-bx=0 经整理,得到参数a和b的计算公式: 6-∑y-∑2 nx-(∑x) (10-8) n [例10-2]利用表(10-4)所给的资料,建立广告费用支出与销售额的一元线性回归方 程。 解:根据表10-4所给出的数据,列出计算表10-5。 表10-5一元线性回归计算表 序号 y x好 6 50 36 300 2 7 58 49 406 2 8 70 64 560 4 4 16 160 5 5 60 25 300 6 2 30 4 60 7 37 0 111 81 合计 44 425 284 2617 将表中数据代入(10-8),得到 b=∑-x∑2 -∑月 =8×2617-44×425 8×284-(44)7 =6.655 n n =425-2473×44 8 8 =16524 于是,广告费与销售额的一元线性回归方程为 8
8 2 ( ) 0 2 ( ) 0 i i i i i Q y a bx a Q y a bx x b Ï ¶ = - - - = Ô Ô ¶ Ì ¶Ô = - - - = ÔÓ ¶ Â Â (10-7) 经整理,得到参数 a 和 b 的计算公式: 2 2 ( )( ) ( ) i i i i i i i i n x y x y b n x x y x a b n n Ï - Ô = Ô - Ì Ô = - Ô Ó Â Â Â Â Â Â Â (10-8) [例 10-2]利用表(10-4)所给的资料,建立广告费用支出与销售额的一元线性回归方 程。 解:根据表 10-4 所给出的数据,列出计算表 10-5。 表 10-5 一元线性回归计算表 序号 i x i y 2 i x i i x y 1 6 50 36 300 2 7 58 49 406 3 8 70 64 560 4 4 40 16 160 5 5 60 25 300 6 2 30 4 60 7 3 37 9 111 8 9 80 81 720 合计 44 425 284 2617 将表中数据代入(10-8),得到 2 2 2 ( )( ) ( ) 8 2617 44 425 8 284 (44) 6.655 i i i i i i n x y x y b n x x - = - ¥ - ¥ = ¥ - = Â Â Â Â Â 425 44 2.473 8 8 16.524 i i y x a b n n = - = - ¥ = Â Â 于是,广告费与销售额的一元线性回归方程为

=16.524+6.655x 10.3.3一元线性回归方程的显著性检验 在用最小二乘法求回归直线时,并不需要预先假定y与x之间一定存在线性关系。即 使是平面上一些杂乱无章的点也可以用(10-8)式配出一条直线。但这是毫无意义的。因 此,我们有必要对回归方程进行显若性检验。回归方程的显著性检验包括两个方面:一是 回归系数的显著性检验:二是回归方程线性关系的整体显著性检验。 1.回归系数b的显著性检验 回归系数b的显若性检验就是要验证总体两变量x与y的线性关系是否真正存在。因此, 我们对线性模型(10-8)提出如下假设: H。:b=0: H1:b≠0 如果原假设H。成立,说明x对y没有影响,回归方程不具有实用价值。如果原假设H。 不成立,则可以认为x对y有显著影响,我们求出线性回归方程是有意义的。 为此,我们需要构造一个检验的统计量。 我们把y的个观测值之间的差异,用观测值,与其平均值的偏差平方和来表示 称为总离差平方和,记为SST sST=2y-列 (10-9) 我们可以将其分解: SST=∑[y-)+(y-,)川 =2戊-列+20y-+22-0y-) (10-10) 不难证明交叉项等于零,若记 sSR=∑(,-) (10-11) ssE=立0-) 则有 SST SSR+SSE (10-12) 这里,SSR叫回归平方和,它反映了回归方程的理论值对平均值的离散程度:SSE叫残 差平方和,它是实际观测值与回归值的离差平方和,反映了随机因素对y取值的影响。 可以证明,当H。成立时。 9
9 yˆ = 16.524 + 6.655x 10.3.3 一元线性回归方程的显著性检验 在用最小二乘法求回归直线时,并不需要预先假定 y 与 x 之间一定存在线性关系。即 使是平面上一些杂乱无章的点也可以用(10-8)式配出一条直线。但这是毫无意义的。因 此,我们有必要对回归方程进行显著性检验。回归方程的显著性检验包括两个方面:一是 回归系数的显著性检验;二是回归方程线性关系的整体显著性检验。 1.回归系数 b 的显著性检验 回归系数b 的显著性检验就是要验证总体两变量x 与y 的线性关系是否真正存在。 因此, 我们对线性模型(10-8)提出如下假设: 0 H : b = 0 ; 1 H : b ¹ 0 如果原假设 H0 成立, 说明 x 对 y 没有影响, 回归方程不具有实用价值。如果原假设H 0 不成立,则可以认为 x 对 y 有显著影响,我们求出线性回归方程是有意义的。 为此,我们需要构造一个检验的统计量。 我们把 y 的 n 个观测值之间的差异,用观测值 i y 与其平均值 y 的偏差平方和来表示, 称为总离差平方和,记为 SST。 2 1 ( ) n i i SST y y = = Â - (10-9) 我们可以将其分解: (10-10) 不难证明交叉项等于零,若记 (10-11) 则有 SST = SSR + SSE (10-12) 这里,SSR 叫回归平方和,它反映了回归方程的理论值对平均值的离散程度 ;SSE 叫残 差平方和,它是实际观测值与回归值的离差平方和,反映了随机因素对 y 取值的影响。 可以证明,当 H0 成立时, 2 1 [( ˆ ) ( ˆ )] n i i i i SST y y y y = = Â - + - 2 2 1 1 1 ( ˆ ) ( ˆ ) 2 ( ˆ )( ˆ ) n n n i i i i i i i i i y y y y y y y y = = = = Â - +Â - + Â - - 2 1 2 1 ( ˆ ) ( ˆ ) n i i n i i i S S R y y S S E y y = = Ï = - Ô Ô Ì Ô = - Ô Ó Â Â

(10-13) SSE /(n-2) 因此,我们可以作出决策,对于给定的显著性水平a,若川>1(n-2),则拒绝H。, 表明x与y之间存在线性关系,x对y的影响时显著的。否则,变量x与y之间不存在线性 关系,x对V的影响不显著, 2.回归方程的显著性检验 回归方程显著性检验,是对回归模型总体的显著性检验,即对回归模型中所有因变量与 自变量之间的线性关系在总体上是否显著成立作出推断。回归方程显著性检验,实际上是对 回归方程拟合优度的检验,采用F统计量,所以又称为F检验。 首先,我们构造统计量 SSR F= SSE/(n-2) (10-14) 当H。为真时,F~F(l,n-2)。 因此,我们可以作出决策,对于给定的显著性水平α,若F>F(L,n-2),则拒绝 H。,表明总体回归方程线性关系成立,总体回归方程是显著的。否则,接受H。,总体回 归方程不显著。 需要说明的是,在一元线性回归中,只有一个自变量,t检验和F检验是一致的。但是 在多元回归分析中,t检验和F检验是不同的。T检验是检验回归方程中回归系数的显著性, F检验则是检验整个方程回归关系的显若性。 [例10-3]根据表10-4的资料拟合的回归方程进行回归系数的显著性检验和回归方程的 显著性检验。 解:(①)回归系数的显著性检验(t检验) 我们提出如下假设: H。:b=0 H1:b≠0 若H。成立,说明广告费对销售额的影响不显著,两者之间不存在线性关系。 在H。成立的条件下,计算t统计量的值 1-y2-的7 43.129 /194.869 -7.568 SSE /(n-2) V6 当显著性水平a=0.05时,4-a2(n-2)=2.4469,此时t=7.568>2.4469,因 此拒绝原假设。说明回归系数是显著的,广告费用和销售额之间的线性关系确实存在,广告 费用是影响销售额的显著因素
10 2 2 [ ( ) ] ~ ( 2) /( 2) b n x x t t n SSE n - = - - (10-13) 因此,我们可以作出决策,对于给定的显著性水平a ,若 1 2 t t (n 2) > - a - ,则拒绝 H0 , 表明 x 与 y 之间存在线性关系,x 对 y 的影响时显著的。否则,变量 x 与 y 之间不存在线性 关系,x 对 y 的影响不显著。 2.回归方程的显著性检验 回归方程显著性检验, 是对回归模型总体的显著性检验,即对回归模型中所有因变量与 自变量之间的线性关系在总体上是否显著成立作出推断。回归方程显著性检验,实际上是对 回归方程拟合优度的检验,采用 F 统计量,所以又称为 F 检验。 首先,我们构造统计量 ( 2) SSR F SSE n = - (10-14) 当 H 0 为真时, F ~ F(1,n - 2) 。 因此,我们可以作出决策,对于给定的显著性水平a ,若 1 F F (1,n 2) > -a - ,则拒绝 H 0 ,表明总体回归方程线性关系成立,总体回归方程是显著的。否则,接受 H 0 ,总体回 归方程不显著。 需要说明的是,在一元线性回归中,只有一个自变量,t 检验和 F 检验是一致的。但是 在多元回归分析中,t 检验和 F 检验是不同的。T 检验是检验回归方程中回归系数的显著性, F 检验则是检验整个方程回归关系的显著性。 [例 10-3]根据表 10-4 的资料拟合的回归方程进行回归系数的显著性检验和回归方程的 显著性检验。 解 :(1) 回归系数的显著性检验(t 检验) 我们提出如下假设: 0 H :b = 0 ; 1 H :b ¹ 0 若 H 0 成立,说明广告费对销售额的影响不显著,两者之间不存在线性关系。 在 H 0 成立的条件下,计算 t 统计量的值 2 2 [ ( ) ] 43.129 7.568 /( 2) 194.869 6 b n x x t SSE n - = = = - 当显著性水平a = 0.05时, 1 2 t (n 2) 2.4469 -a - = ,此时t = 7.568 > 2.4469 ,因 此拒绝原假设。说明回归系数是显著的,广告费用和销售额之间的线性关系确实存在,广告 费用是影响销售额的显著因素