
第三章 统计数据分布特征的描述 学习目标: ·1、熟练掌握反映统计数据分布集中趋势的各种 平均指标的涵义及其计算方法; ÷2、熟练掌握反映统计数据分布离中趋势的各种 变异指标的涵义及其计算方法: ·3、熟练掌握反映统计数据分布对称与偏斜程度 的偏度和峰度指标的涵义及其计算方法
第三章 统计数据分布特征的描述 学习目标: 1、熟练掌握反映统计数据分布集中趋势的各种 平均指标的涵义及其计算方法; 2、熟练掌握反映统计数据分布离中趋势的各种 变异指标的涵义及其计算方法; 3、熟练掌握反映统计数据分布对称与偏斜程度 的偏度和峰度指标的涵义及其计算方法

第三章 统计数据分布特征的描述 ÷3.1 统计变量集中趋势的测定 ×3.2 统计变量离散程度的测定 ÷3.3 变量分布偏度与峰度的描述
第三章 统计数据分布特征的描述 3.1 统计变量集中趋势的测定 统计变量集中趋势的测定 3.2 统计变量离散程度的测定 3.3 变量分布偏度与峰度的描述

3.1统计变量集中趋势的测定 3.1.1 测定集中趋势的主要指标及其作用 3.1.2 位置平均数 3.1.3 数值平均数
3.1 统计变量集中趋势的测定 统计变量集中趋势的测定 3.1.1 3.1.1 测定集中趋势的主要指标及其作用 3.1.2 位置平均数 3.1.3 数值平均数

3.1.1 测定集中趋势的主要指标及其作用 测定集中趋势的指标有两类:位置平均数和数值平均数。 位置平均数是根据变量值位置来确定的代表值,即在总体中将 变量值按顺序排列得到的数列中某个特殊位置的值就称为位置平均 数。常用的位置平均数有众数、中位数和分位数等,前两种常用。 位置平均数可以用于对品质数据和数量数据的测度。 数值平均数就是均值,它是对总体中的所有数据计算平均值, 用以反映所有数据的一般水平。根据计算方法不同,数值平均数可 以分为算术平均数、调和平均数、几何平均数和幂平均数。这类平 均数的特点是,统计总体中任何一项数据的变动都会在一定程度上 影响到数值平均数的计算结果。数值平均数只能用于对数量数据的 测度
3.1.1 测定集中趋势的主要指标及其作用 测定集中趋势的指标有两类:位置平均数和数值平均数。 位置平均数是根据变量值位置来确定的代表值,即在总体中将 变量值按顺序排列得到的数列中某个特殊位置的值就称为位置平均 数。常用的位置平均数有众数、中位数和分位数等,前两种常用。 位置平均数可以用于对品质数据和数量数据的测度。 数值平均数就是均值,它是对总体中的所有数据计算平均值, 用以反映所有数据的一般水平。根据计算方法不同,数值平均数可 以分为算术平均数、调和平均数、几何平均数和幂平均数。这类平 均数的特点是,统计总体中任何一项数据的变动都会在一定程度上 影响到数值平均数的计算结果。数值平均数只能用于对数量数据的 测度

3.1.1 测定集中趋势的主要指标及其作用 测定集中趋势是为了表示社会经济现象总体各单位某一标志在 一定时间、地点条件下所达到的一般水平。亦即将总体各单位标志 值的数量差异抽象化,反映总体在具体条件下各单位标志值达到的 一般水平。 集中趋势的指标经常被作为评价事物和决策的数量标准或参考。 具体地说,测定集中趋势的作用如下: 1.反映总体各单位变量分布的集中趋势和一般水平; 2.比较同类现象在不同单位的发展水平; 3.比较同类现象在不同时期的发展变化趋势或规律, 4.分析现象之间的依存关系
3.1.1 测定集中趋势的主要指标及其作用 测定集中趋势是为了表示社会经济现象总体各单位某一标志在 一定时间、地点条件下所达到的一般水平。亦即将总体各单位标志 值的数量差异抽象化,反映总体在具体条件下各单位标志值达到的 一般水平。 集中趋势的指标经常被作为评价事物和决策的数量标准或参考。 具体地说,测定集中趋势的作用如下: 1.反映总体各单位变量分布的集中趋势和一般水平; 2.比较同类现象在不同单位的发展水平; 3.比较同类现象在不同时期的发展变化趋势或规律; 4.分析现象之间的依存关系

3.1.2位置平均数 位置平均数是根据数据排列位置所确定的代表值, 其与数值平均数的基本区别在于不需要依据每一个数据值 来计算。 常用的位置平均数有: 1、众数 2、中位数 3、其它分位数
3.1.2 位置平均数 位置平均数是根据数据排列位置所确定的代表值, 其与数值平均数的基本区别在于不需要依据每一个数据值 来计算。 常用的位置平均数有: 1、众数 2、中位数 3、其它分位数

3.1.2.1众数(mode) 众数是总体中出现次数最多的那个数据值。在频数分布中,众数指 频数或频率最大的标志值,用Mo表示。 从数据的分布层面看,分布数列中最常出现的标志值说明该标志值 最具有代表性,因此可以反映数列的一般水平。在分配曲线图上,众数 就是曲线的最高峰所对应的标志值。但是,众数具有不确定性。如果数 据的分布没有明显的集中趋势或最高峰点,众数就不存在;如果有多个 高峰点,就有多众数。 在不等距分组的条件下,众数必须根据频数密度或频率密度来计算。 众数是按照数据的位置计算的,它的长处是易于理解,不受极端数 值的影响。当数据分布存在明显的集中趋势,且有显著的极端值时,适 合使用众数。但是其灵敏度、计算功能和稳定性差,具有不唯一性,所 以当数据分布的集中趋势不明显或存在两个以上分布中心时,便不适合 使用众数(前者无众数,后者为双众数或多众数,也等于没有众数)
3.1.2.1 众数(mode) 众数是总体中出现次数最多的那个数据值。在频数分布中,众数指 频数或频率最大的标志值,用Mo表示。 从数据的分布层面看,分布数列中最常出现的标志值说明该标志值 最具有代表性,因此可以反映数列的一般水平。 在分配曲线图上,众数 就是曲线的最高峰所对应的标志值。但是,众数具有不确定性。如果数 据的分布没有明显的集中趋势或最高峰点,众数就不存在;如果有多个 高峰点,就有多众数。 在不等距分组的条件下,众数必须根据频数密度或频率密度来计算。 众数是按照数据的位置计算的,它的长处是易于理解,不受极端数 值的影响。当数据分布存在明显的集中趋势,且有显著的极端值时,适 合使用众数。但是其灵敏度、计算功能和稳定性差,具有不唯一性,所 以当数据分布的集中趋势不明显或存在两个以上分布中心时,便不适合 使用众数(前者无众数,后者为双众数或多众数,也等于没有众数)
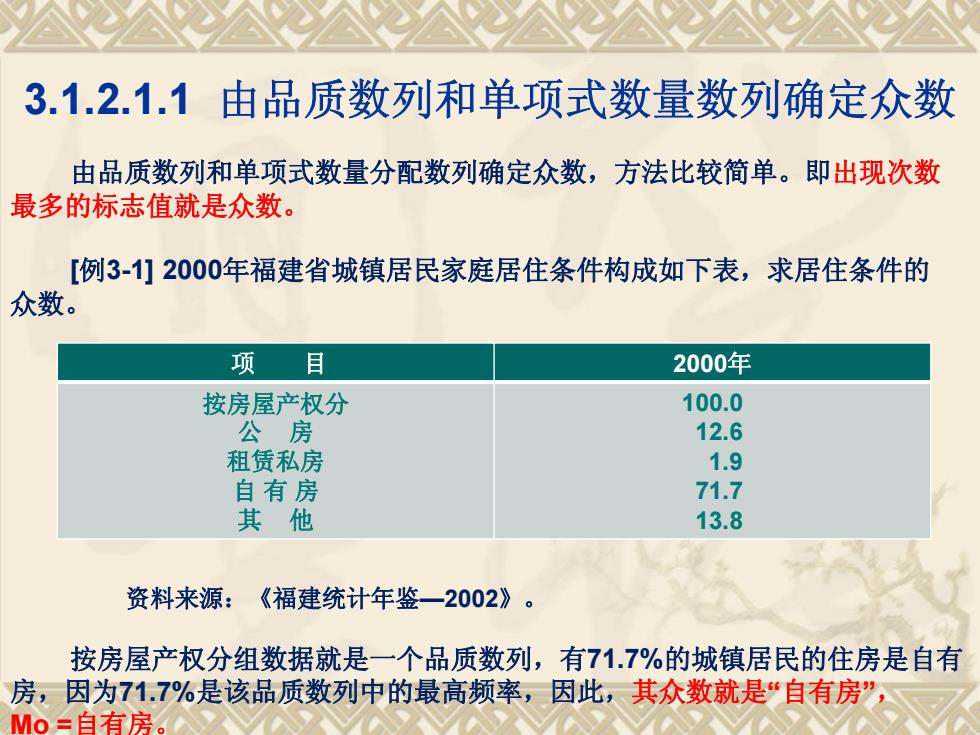
3.1.2.1.1 由品质数列和单项式数量数列确定众数 由品质数列和单项式数量分配数列确定众数,方法比较简单。即出现次数 最多的标志值就是众数。 [例3-1]2000年福建省城镇居民家庭居住条件构成如下表,求居住条件的 众数。 项 目 2000年 按房屋产权分 100.0 公房 12.6 租赁私房 1.9 自有房 71.7 其他 13.8 资料来源:《福建统计年鉴一2002》。 按房屋产权分组数据就是一个品质数列,有71.7%的城镇居民的住房是自有 房,因为717%是该品质数列中的最高频率,因此,其众数就是“自有房”, M0=自有房
3.1.2.1.1 由品质数列和单项式数量数列确定众数 由品质数列和单项式数量分配数列确定众数,方法比较简单。即出现次数 最多的标志值就是众数。 [例3-1] 2000年福建省城镇居民家庭居住条件构成如下表,求居住条件的 众数。 表3-1 城镇居民家庭居住条件构成 (单位:%) 资料来源:《福建统计年鉴—2002》。 按房屋产权分组数据就是一个品质数列,有71.7%的城镇居民的住房是自有 房,因为71.7%是该品质数列中的最高频率,因此,其众数就是“自有房”, Mo =自有房。 项 目 2000年 按房屋产权分 公 房 租赁私房 自有房 其 他 100.0 12.6 1.9 71.7 13.8

3.1.2.1.1由品质数列和单项式数量数列确定众数 [例3-2]某学院某学年教师开课门数如表3-2,求开课门数的众 数。 表3-2 教师开课门数 (单位:门) 开课门数x 1 2 3 4 合计 教师数f 15 30 28 12 85 在上表的单项式数量数列中,教师开课门数最集中的是2门课, 所以2就是众数,M0=2
3.1.2.1.1 由品质数列和单项式数量数列确定众数 [例3-2] 某学院某学年教师开课门数如表3-2,求开课门数的众 数。 表3-2 教师开课门数 (单位:门) 在上表的单项式数量数列中,教师开课门数最集中的是2门课, 所以2就是众数, Mo =2。 开课门数 x 1 2 3 4 合计 教师数f 15 30 28 12 85

3.1.2.1.2 由组距数量数列确定众数 [例3-3]某地区农民收入情况如表3-3,计算其人均纯 收入的众数。 表3-3 农民家庭年人均纯收入情况表 按年人均纯收入分组(元) 农民家庭数(户) 1000-1200 240 1200-1400 480 1400-1600 1050 1600-1800 600 1800-2000 270 2000-2200 210 2200-2400 120 2400-2600 30 合 计 3000
3.1.2.1.2 由组距数量数列确定众数 按年人均纯收入分组(元) 农民家庭数(户) 1000-1200 1200-1400 1400-1600 1600-1800 1800-2000 2000-2200 2200-2400 2400-2600 240 480 1050 600 270 210 120 30 合 计 3000 [例3-3]某地区农民收入情况如表3-3,计算其人均纯 收入的众数。 表3-3 农民家庭年人均纯收入情况表