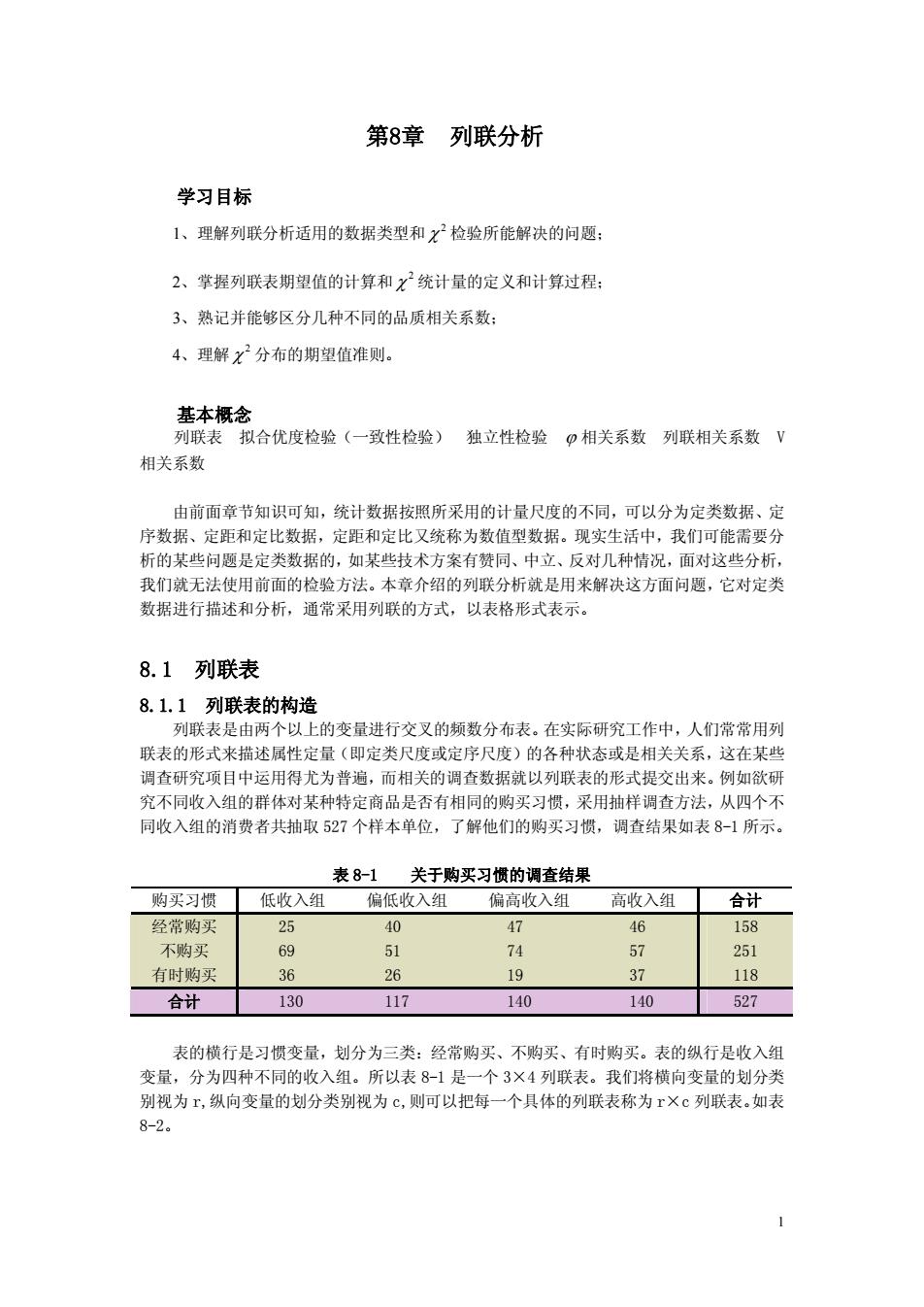
第8章列联分析 学习目标 1、理解列联分析适用的数据类型和x2检验所能解决的问题: 2、掌握列联表期望值的计算和X统计量的定义和计算过程: 3、熟记并能够区分几种不同的品质相关系数 4、理解X分布的期望值准则。 基太概念 列联表拟合优度检验(一致性检验)独立性检验口相关系数列联相关系数V 相关系数 由前面章节知识可知,统计数据按照所采用的计量尺度的不同,可以分为定类数据、定 序数据、定距和定比数据,定距和定比又统称为数值型数据。现实生活中,我们可能需要分 析的某些问题是定类数据的,如某些技术方案有赞同、中立、反对几种情况,面对这些分析 我们就无法使用前面的检验方法。本章介绍的列联分析就是用来解决这方面问题,它对定类 数据进行描述和分析,通常采用列联的方式,以表格形式表示。 8.1列联表 8.1.1列联表的构造 列联表是由两个以上的变量进行交叉的频数分布表。在实际研究工作中,人们常常用列 联表的形式来描述属性定量(即定类尺度或定序尺度)的各种状态或是相关关系,这在某些 调查研究项目中运用得尤为普遍,而相关的调查数据就以列联表的形式提交出来。例如欲研 究不同收入组的群体对某种特定商品是否有相同的购买习惯,采用抽样调杏方法,从四个不 同收入组的消费者共抽取527个样本单位, 了解他们的购买习惯,调查结果如表8-1所示。 表8-1 关于购买习惯的调查结果 购买习惯低收入组 偏低收入组偏高收入组 高收入组合计 经常购买 25 47 不购买 57 有时购买 36 26 19 37 118 合计 130 117 140 140 527 表的横行是习惯变量,划分为三类:经常购买、不购买、有时购买。表的纵行是收入组 变量,分为四种不同的收入组。所以表8-1是一个3×4列联表。我们将横向变量的划分类 别视为工,纵向变量的划分类别视为c,则可以把每一个具体的列联表称为r×c列联表.如表 8-2
1 第8章 列联分析 学习目标 1、理解列联分析适用的数据类型和 2 c 检验所能解决的问题; 2、掌握列联表期望值的计算和 2 c 统计量的定义和计算过程; 3、熟记并能够区分几种不同的品质相关系数; 4、理解 2 c 分布的期望值准则。 基本概念 列联表 拟合优度检验(一致性检验) 独立性检验 j 相关系数 列联相关系数 V 相关系数 由前面章节知识可知,统计数据按照所采用的计量尺度的不同,可以分为定类数据、定 序数据、定距和定比数据,定距和定比又统称为数值型数据。现实生活中,我们可能需要分 析的某些问题是定类数据的,如某些技术方案有赞同、中立、反对几种情况,面对这些分析, 我们就无法使用前面的检验方法。本章介绍的列联分析就是用来解决这方面问题,它对定类 数据进行描述和分析,通常采用列联的方式,以表格形式表示。 8.1 列联表 8.1.1 列联表的构造 列联表是由两个以上的变量进行交叉的频数分布表。 在实际研究工作中,人们常常用列 联表的形式来描述属性定量(即定类尺度或定序尺度)的各种状态或是相关关系,这在某些 调查研究项目中运用得尤为普遍,而相关的调查数据就以列联表的形式提交出来。例如欲研 究不同收入组的群体对某种特定商品是否有相同的购买习惯,采用抽样调查方法,从四个不 同收入组的消费者共抽取 527 个样本单位,了解他们的购买习惯,调查结果如表 8-1 所示。 表 8-1 关于购买习惯的调查结果 购买习惯 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 不购买 有时购买 25 40 47 46 69 51 74 57 36 26 19 37 158 251 118 合计 130 117 140 140 527 表的横行是习惯变量,划分为三类:经常购买、不购买、有时购买。表的纵行是收入组 变量,分为四种不同的收入组。所以表 8-1 是一个 3×4 列联表。我们将横向变量的划分类 别视为 r,纵向变量的划分类别视为 c,则可以把每一个具体的列联表称为 r×c 列联表。 如表 8-2
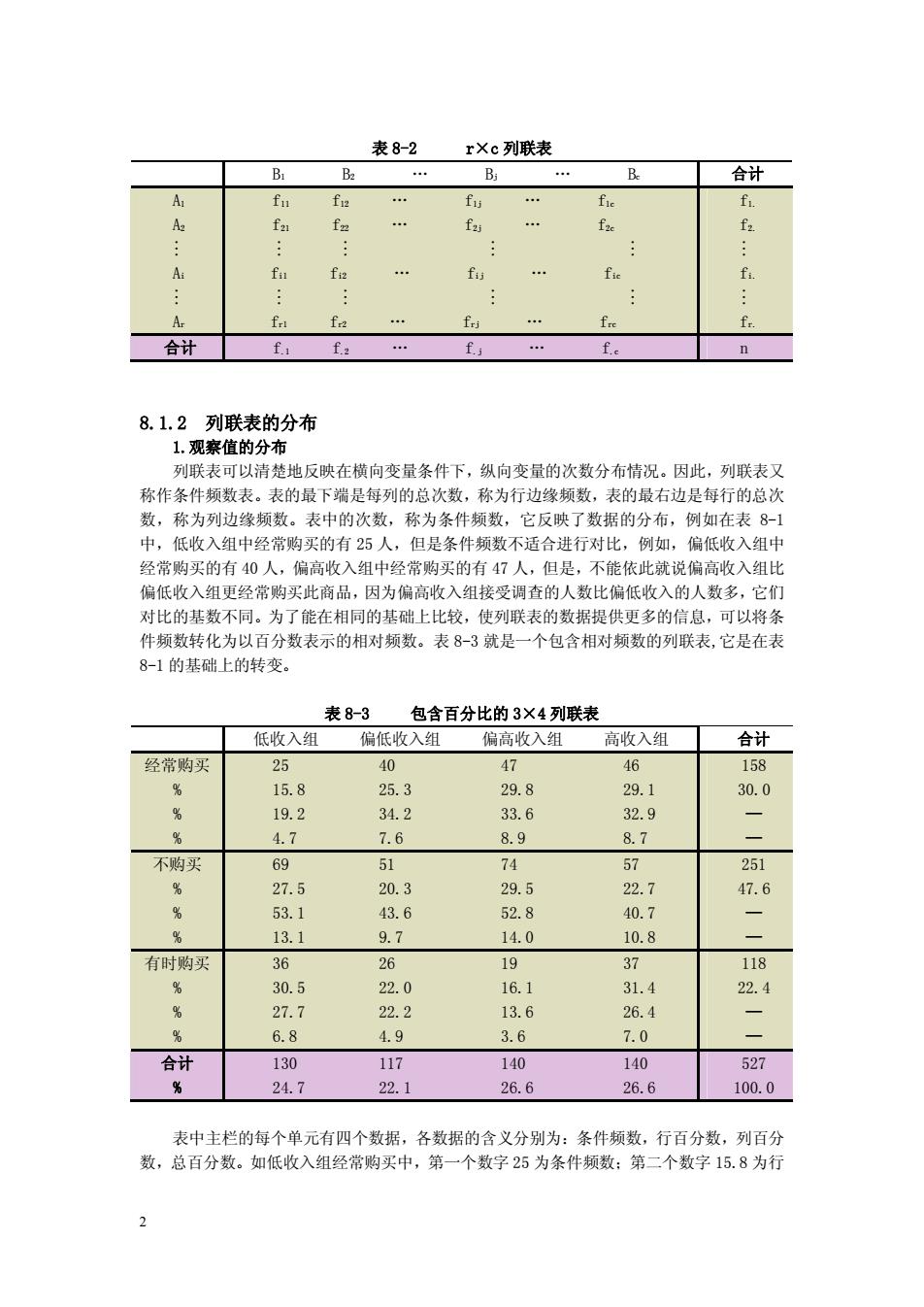
表8-2 rXc列联表 B 合计 f f f fa 合计 fa f f 8.1.2列联表的分布 1观察值的分布 列联表可以清楚地反映在横向变量条件下,纵向变量的次数分布情况。因此,列联表又 称作条件须数表。表的最下端是每列的总次数,称为行边缘频数,表的最右边是每行的总 数,称为列边缘频数。表中的次数,称为条件频数,它反映了数据的分布,例如在表8-1 中,低收入组中经常购买的有25人,但是条件频数不适合进行对比,例如,偏低收入组中 经常购买的有40人,偏高收入组中经常购买的有47人,但是,不能依此就说偏高收入组比 偏低收入组更经常购买此商品,因为偏高收入组接受调查的人数比偏低收入的人数多,它们 对比的基数不同。为了能在相同的基础上比较,使列联表的数据提供更多的信息,可以将条 件烦数转化为以百分数表示的相对烦数。表8-3就是一个包含相对顿数的列联表,它是在表 8-1的基础上的转变。 表8-3 包含百分比的3×4列联表 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 25 40 47 46 158 158 253 208 2g1 30.0 192 3492 336 32.9 4.7 7.6 89 8.7 不购买 69 51 74 吟 251 275 203 29.5 227 47.6 53.1 43.6 528 40.7 13.1 9.7 14.0 10.8 有时购买 36 26 19 37 118 30.5 22.0 16.1 31.4 22.4 27.7 22.2 13.6 26.4 6.8 4.9 3.6 7.0 合计 130 117 140 140 527 24.7 22.1 26.6 26.6 100.0 表中主栏的每个单元有四个数据,各数据的含义分别为:条件频数,行百分数,列百分 数,总百分数。如低收入组经常购买中,第一个数字25为条件频数:第二个数字15.8为行
2 表 8-2 r×c 列联表 B1 B2 . Bj . Bc 合计 A1 A2 M Ai M Ar f11 f12 . f1j . f1c f21 f22 . f2j . f2c M M M M fi1 fi2 . fij . fic M M M M fr1 fr2 . frj . frc f1. f2. M fi. M fr. 合计 f.1 f.2 . f.j . f.c n 8.1.2 列联表的分布 1.观察值的分布 列联表可以清楚地反映在横向变量条件下,纵向变量的次数分布情况。因此,列联表又 称作条件频数表。表的最下端是每列的总次数,称为行边缘频数,表的最右边是每行的总次 数,称为列边缘频数。表中的次数,称为条件频数,它反映了数据的分布,例如在表 8-1 中,低收入组中经常购买的有 25 人,但是条件频数不适合进行对比,例如,偏低收入组中 经常购买的有 40 人,偏高收入组中经常购买的有 47 人,但是,不能依此就说偏高收入组比 偏低收入组更经常购买此商品, 因为偏高收入组接受调查的人数比偏低收入的人数多,它们 对比的基数不同。为了能在相同的基础上比较,使列联表的数据提供更多的信息,可以将条 件频数转化为以百分数表示的相对频数。表 8-3 就是一个包含相对频数的列联表,它是在表 8-1 的基础上的转变。 表 8-3 包含百分比的 3×4 列联表 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 % % % 25 40 47 46 15.8 25.3 29.8 29.1 19.2 34.2 33.6 32.9 4.7 7.6 8.9 8.7 158 30.0 — — 不购买 % % % 69 51 74 57 27.5 20.3 29.5 22.7 53.1 43.6 52.8 40.7 13.1 9.7 14.0 10.8 251 47.6 — — 有时购买 % % % 36 26 19 37 30.5 22.0 16.1 31.4 27.7 22.2 13.6 26.4 6.8 4.9 3.6 7.0 118 22.4 — — 合计 % 130 117 140 140 24.7 22.1 26.6 26.6 527 100.0 表中主栏的每个单元有四个数据,各数据的含义分别为:条件频数,行百分数,列百分 数,总百分数。如低收入组经常购买中,第一个数字 25 为条件频数;第二个数字 15.8 为行

百分数,即25/158=15.8%:第三个数字19.2为列百分数,即25/130=19.2%:第四个数字 4.7为总百分数,即25/527=4.7%。在最右边和最下边的合计栏中各有两行数据,第一行是 边缘频数,第二行是边缘频数的百分数。如最右边的30.0%158/527,最下边的24.7%=130/ 527。这里我们分析的是观察值的分布,但是仅仅依赖这些还难以进行深入的分析,为此我 们引入期型分布的概念。 2.期望值的分布 仍以前例为例。在全部527个总体中,经常购买的有158个,占总数的30.0%,但我们 希望了解各收入组购买习惯是否存在差异。如果各收入组的购买习惯相同,那么对于低收入 组中经常购买的人数应当为130×30.0%39人,偏低收入组中经常购买的人数应当为117 30%=35人,这39人和35人就是本例中的期望值。按此计算可得各个单元期望值的分布, 如表8-4。 表8-4期望值分布表 低收入 偏低收入组 偏高收入组 高收入组 0.300 0.300 0.300 0.300 经常购买的 130 ×117 ×140 140 期望值 39 35 49 42 0.476 0.476 0.476 0.476 不购买的 ×130 X117 ×140 ×140 期望值 62 56 67 67 有时购买的 0.224 0.224 0.224 0.224 130 117 140 140 期型值 29 26 31 31 观察值和期望值分布得出后,接下来对列联表中的变量进行分析,这时可以采用统计分 析方法。列联表分析的统计分析方法很多,除了Pearson检验、校正X2检验、Fisher 的精确检验外,还有秩和检验、Ridit分析、对应分析、Kappa检验等。由于分析方法繁多 且复杂,本书仅说明实际中适用范围最广的X检验。 82x分布与x检验 8.2.1x分布 X分布是在统计学中经常用到的一种统计分布。假设X,X,·,X。是n个相互独立 的随机变量,且X,口N(0,1),1=1,2,.,n,那么我们就定义X=X2+X,2+.+X2服 从自由度为n的x2分布,记作X口x2(n) 8.2.2x2统计量 3
3 百分数,即 25/158=15.8%;第三个数字 19.2 为列百分数,即 25/130=19.2%;第四个数字 4.7 为总百分数,即 25/527=4.7%。在最右边和最下边的合计栏中各有两行数据,第一行是 边缘频数,第二行是边缘频数的百分数。如最右边的 30.0%=158/527,最下边的 24.7%=130/ 527。这里我们分析的是观察值的分布,但是仅仅依赖这些还难以进行深入的分析,为此我 们引入期望分布的概念。 2.期望值的分布 仍以前例为例。在全部 527 个总体中,经常购买的有 158 个,占总数的 30.0%,但我们 希望了解各收入组购买习惯是否存在差异。如果各收入组的购买习惯相同, 那么对于低收入 组中经常购买的人数应当为 130×30.0%=39 人,偏低收入组中经常购买的人数应当为 117× 30%=35 人,这 39 人和 35 人就是本例中的期望值。按此计算可得各个单元期望值的分布, 如表 8-4。 表 8-4 期望值分布表 低收入组 偏低收入组 偏高收入组 高收入组 经常购买的 期望值 0.300 × 130 39 0.300 × 117 35 0.300 × 140 42 0.300 × 140 42 不购买的 期望值 0.476 × 130 62 0.476 × 117 56 0.476 × 140 67 0.476 × 140 67 有时购买的 期望值 0.224 × 130 29 0.224 × 117 26 0.224 × 140 31 0.224 × 140 31 观察值和期望值分布得出后,接下来对列联表中的变量进行分析, 这时可以采用统计分 析方法。列联表分析的统计分析方法很多,除了 Pearson 2 c 检验、校正 2 c 检验、Fisher 的精确检验外,还有秩和检验、Ridit 分析、对应分析、Kappa 检验等。由于分析方法繁多 且复杂,本书仅说明实际中适用范围最广的 2 c 检验。 8.2 2 c 分布与 2 c 检验 8.2.1 2 c 分布 2 c 分布是在统计学中经常用到的一种统计分布。假设 1 2 , , X X ., Xn 是 n 个相互独立 的随机变量,且 Xi : N (0,1) ,i =1,2,. , n ,那么我们就定义 2 2 2 X = X1 + X2 +. + Xn 服 从自由度为n 的 2 c 分布,记作 2 X : c (n) 。 8.2.2 2 c 统计量
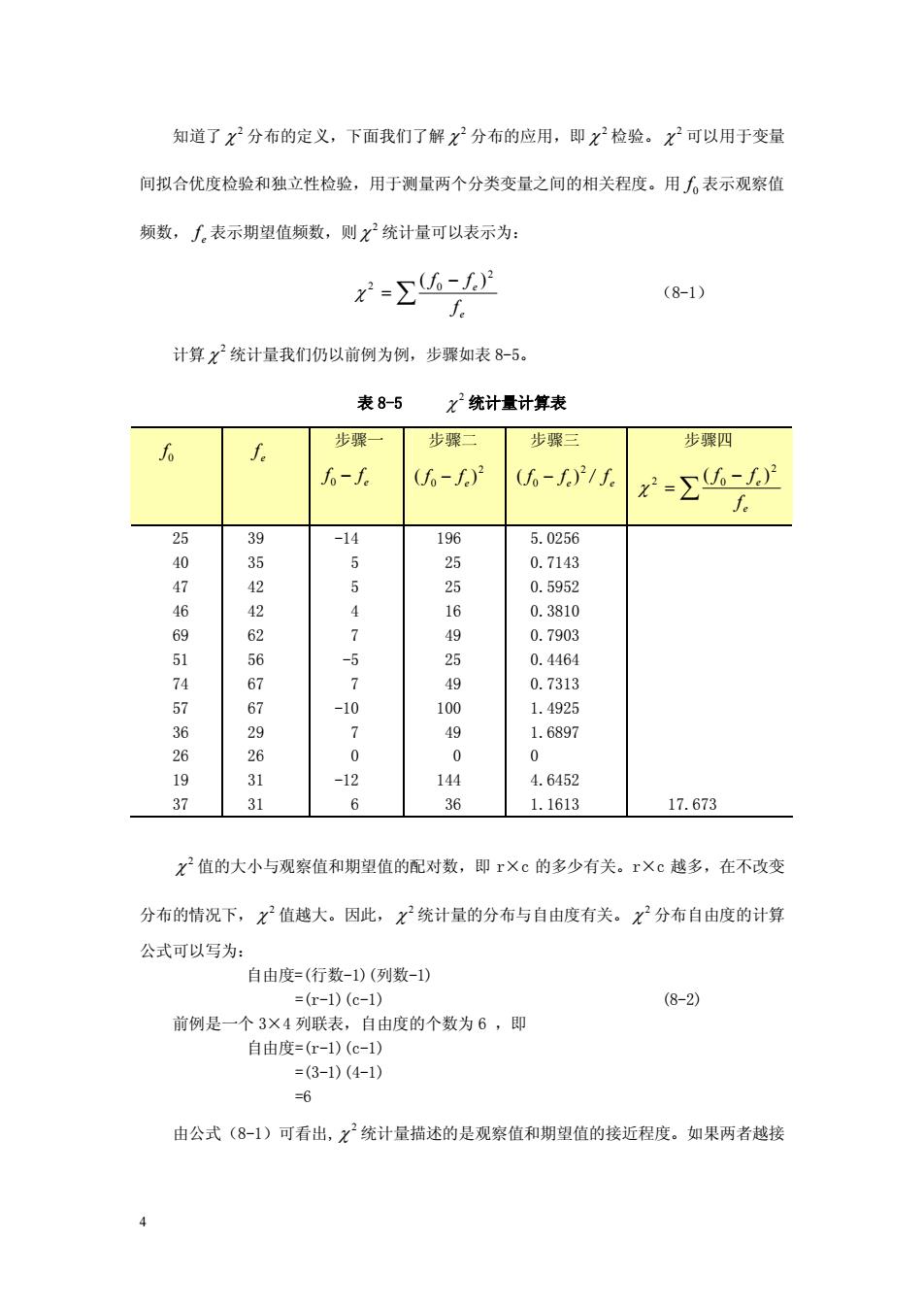
知道了x分布的定义,下面我们了解父2分布的应用,即x检验。X2可以用于变量 间拟合优度检验和独立性检验,用于测量两个分类变量之间的相关程度。用表示观察值 频数,∫。表示期望值频数,则x统计量可以表示为: =∑6- (8-1) f。 计算义己统计量我们仍以前例为例,步骤如表8-5。 表8-5 x统计量计算表 步骤一 步骤二 步骤三 步强四 fo-f (6-) -)21f x=∑- 25 39 -14 196 5.0256 35 0.7143 47 42 0.5952 0.3810 62 7 0.7903 -5 24 0.446 0.7313 67 100 1.4925 7 1.6897 名 26 0 0 0 19 31 -12 144 4.6452 37 31 6 36 1.1613 17.673 X值的大小与观察值和期望值的配对数,即r×c的多少有关。r×c越多,在不改变 分布的情况下,X值越大。因此,X统计最的分布与自由度有关。X分布自由度的计算 公式可以写为: 自由度=(行数-1)(列数-1) =r-1)(c-1) (8-2) 前例是一个3×4列联表,自由度的个数为6,即 自由度=(r-1)(c-1) =(3-1)(4-1 6 由公式(8-1)可看出,X统计量描述的是观察值和期望值的接近程度。如果两者越接
4 知道了 2 c 分布的定义,下面我们了解 2 c 分布的应用,即 2 c 检验。 2 c 可以用于变量 间拟合优度检验和独立性检验,用于测量两个分类变量之间的相关程度。用 0 f 表示观察值 频数, e f 表示期望值频数,则 2 c 统计量可以表示为: Â - = e e f f f 2 2 0 ( ) c (8-1) 计算 2 c 统计量我们仍以前例为例,步骤如表 8-5。 表 8-5 2 c 统计量计算表 0 f e f 步骤一 e f - f 0 步骤二 2 0 ( ) e f - f 步骤三 2 0 ( ) e f - f / e f 步骤四 Â - = e e f f f 2 2 0 ( ) c 25 40 47 46 69 51 74 57 36 26 19 37 39 35 42 42 62 56 67 67 29 26 31 31 -14 5 5 4 7 -5 7 -10 7 0 -12 6 196 25 25 16 49 25 49 100 49 0 144 36 5.0256 0.7143 0.5952 0.3810 0.7903 0.4464 0.7313 1.4925 1.6897 0 4.6452 1.1613 17.673 2 c 值的大小与观察值和期望值的配对数,即 r×c 的多少有关。r×c 越多,在不改变 分布的情况下, 2 c 值越大。因此, 2 c 统计量的分布与自由度有关。 2 c 分布自由度的计算 公式可以写为: 自由度=(行数-1)(列数-1) =(r-1)(c-1) (8-2) 前例是一个 3×4 列联表,自由度的个数为 6 ,即 自由度=(r-1)(c-1) =(3-1)(4-1) =6 由公式(8-1)可看出, 2 c 统计量描述的是观察值和期望值的接近程度。如果两者越接

近,即。-的绝对值越小,计算出的x越小:反之,如果。-f的绝对值越大,计算 出的越大。X检验正是运用X的计算结果与X分布中的临界值进行比较,做出对原 假设接受或拒绝的统计决策。 8.2.3X2检验 x2统计量是由皮尔逊(Pearson)引入的,故我们也叫它皮尔逊统计量,其实按式(8-1) 定义的函数自身并不服从x2分布,但是皮尔逊证明了它的极限分布为X分布。在应用中, 只要样本量充分大时,X统计量渐近地服从X分布,因此我们可以就其进行检验, 根据列联表的不同内容,可以进行拟合优度检验(一致性检验)和独立性检验。从表面 上看,一致性检验和独立性检验不论在列联表的形式上,还是在计算x的公式上都是相同 的,所以经常被笼统地称为X检验。但是两者还是存在差异的。 首先,两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行,依照各类别分 别计算其比例,则属于拟合优度检验。如果抽样时并未事先分类,抽样后根据研究内容,把 入选单位按两类变量进行分类,形成列联表,则是独立性检验。 其次,两种检验假设的内容有所差异。对于拟合优度检验,原假设通常是假设个类别总 体比例等于某个期望概率,而独立性检验中原假设则假设两个变量之间独立。 最后,期望频数的计算 在拟合优度检验中是利用原假设中的期望概率,用观察频数乘 以期望概率,直接得到期望须数独立性检验中两个水平的联合概率是两个单独概率的乘积。 1,拟合优度检验 如果样本是从总体的不同类别中分别抽取,研究目的是对不同类别的目标量之间是否存 在显艺性差异讲行检验,我们就把它称为拟合优度检验,在某些书上也叫做一致性检验。前 面举的例子中,如果我们要检验四个收入组中购买习惯是否一致,就是要检验在不同的购买 习惯上比例是否一致,下边我们将其作为 一个例子来了解拟合优度检验 [例81]欲研究不同收入群体对某种特定商品是否有相同的购买习惯,市场调查人员 调查了四个不同收入组的消费者共527人,购买习惯分为:经常购买、不购买、有时购买。 调查结果如表8-1,以ā=0.1的显著性水平检验不同收入群体中的购买习惯是否存在差异。 :如果不存在差异,四个收入水平的购买习惯应该是一致的,所以原假设和备选假设 分别为 Hh:Pi=P:=P=P4 H:P、P、P、P不全相等 由式(8-1)得 2=Σ6-D1.6m3 由式(8-2)得 自由度=(r-1)(c-1)=(3-1)(4-1)=6 因为a=0.1,查表得x6:(6)=10.645。由于x2>x2,故拒绝原假设,即认为不同收 5
5 近,即 e f - f 0 的绝对值越小,计算出的 2 c 越小;反之,如果 e f - f 0 的绝对值越大,计算 出的 2 c 越大。 2 c 检验正是运用 2 c 的计算结果与 2 c 分布中的临界值进行比较,做出对原 假设接受或拒绝的统计决策。 8.2.3 2 c 检验 2 c 统计量是由皮尔逊 (Pearson) 引入的, 故我们也叫它皮尔逊统计量, 其实按式 (8-1) 定义的函数自身并不服从 2 c 分布,但是皮尔逊证明了它的极限分布为 2 c 分布。在应用中, 只要样本量充分大时, 2 c 统计量渐近地服从 2 c 分布,因此我们可以就其进行 2 c 检验。 根据列联表的不同内容,可以进行拟合优度检验(一致性检验)和独立性检验。从表面 上看,一致性检验和独立性检验不论在列联表的形式上,还是在计算 2 c 的公式上都是相同 的,所以经常被笼统地称为 2 c 检验。但是两者还是存在差异的。 首先,两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行,依照各类别分 别计算其比例,则属于拟合优度检验。如果抽样时并未事先分类,抽样后根据研究内容,把 入选单位按两类变量进行分类,形成列联表,则是独立性检验。 其次,两种检验假设的内容有所差异。对于拟合优度检验,原假设通常是假设个类别总 体比例等于某个期望概率,而独立性检验中原假设则假设两个变量之间独立。 最后,期望频数的计算。在拟合优度检验中是利用原假设中的期望概率,用观察频数乘 以期望概率, 直接得到期望频数。 独立性检验中两个水平的联合概率是两个单独概率的乘积。 1.拟合优度检验 如果样本是从总体的不同类别中分别抽取, 研究目的是对不同类别的目标量之间是否存 在显著性差异进行检验,我们就把它称为拟合优度检验,在某些书上也叫做一致性检验。前 面举的例子中,如果我们要检验四个收入组中购买习惯是否一致, 就是要检验在不同的购买 习惯上比例是否一致,下边我们将其作为一个例子来了解拟合优度检验。 [例 8-1 ]欲研究不同收入群体对某种特定商品是否有相同的购买习惯,市场调查人员 调查了四个不同收入组的消费者共 527 人,购买习惯分为:经常购买、不购买、有时购买。 调查结果如表 8-1,以α=0.1 的显著性水平检验不同收入群体中的购买习惯是否存在差异。 解:如果不存在差异,四个收入水平的购买习惯应该是一致的,所以原假设和备选假设 分别为: H0: P1=P2 =P3=P4; H1: P1、P2 、P3、P4不全相等 由式(8-1)得 Â - = e e f f f 2 2 0 ( ) c =17.673 由式(8-2)得 自由度=(r-1)(c-1)=(3-1)(4-1)=6 因为α=0.1,查表得 (6) 10. 645 2 c 0. 1 = 。由于 2 2 c > c a ,故拒绝原假设,即认为不同收

入群的购买习惯不是一致的。 拟合优度检验除了可以检验各类别的之间的概率是否相等,还可以应用到下列几种场 合 (1)检验假设分布的概率 假设某因素各种分类的频数分布为某一理论分布(如正态分布),检验实际次数与理论 上期望的结果之间是否有显著差异。 (2)连续变最分布的拟合度拾验 对于连续随机变量的一组测量数据,有时需要对其频数分布究竟符合哪种理论频数的分 布进行探讨,这时,就要用到拟合度检验 (3)资料用百分数表示的拟合度检验 如果收集到的频数资料已经转成百分数,这时拟合度检验的方法与上述几种情况基本相 同,只是最后将计算的卡方值乘以N/100(N表示总体数)后再查卡方表。 以下情况(1)我1再看一个捌子 [例8-2]随机抽取了2000年1月出生的男50名,分别测出他们的体重,并算出样 本均值为x=3160g,未修正样本方差为s=465.5。按体重分组如表8-6,试以这些观察数 据判断新生男赞的体重是否服从正态分布(显著性水平ā=0.05). 表86 新生男婴体重调查结果 体重分组(g) 组中值M, 领数。 3700以上 3825 3450-3700 3575 3200-3450 3325 10 2950-3200 3075 12 2700-2950 2825 7 2450-2700 2575 2450以下 2325 解:由题意我们得出原假设和备选假设如下: :新生男堡的体重符合正态分布 :新生男婴的体重不符合正态分布 在原假设条件成立的前提下,即符合正态分布,那么立=x,G2=s子。按如下步骤 算: (1)求各组组中值M,和平均数x的离差X,即X=M,-x: (2)求各离差的标准分值Z,=X,/5=(M,-x)/50,i=L,2,.,6: (3)由分值计算④。(Z,),1=1,2,6。并且假定④(Z。)=0,Φ。(Z,)=1: (4)计算p,=Φ(亿,)-①(亿,),1l,2,.,7。从而进一步得到f.=N×P,:
6 入群的购买习惯不是一致的。 拟合优度检验除了可以检验各类别的之间的概率是否相等,还可以应用到下列几种场 合: (1)检验假设分布的概率 假设某因素各种分类的频数分布为某一理论分布(如正态分布),检验实际次数与理论 上期望的结果之间是否有显著差异。 (2)连续变量分布的拟合度检验 对于连续随机变量的一组测量数据, 有时需要对其频数分布究竟符合哪种理论频数的分 布进行探讨,这时,就要用到拟合度检验。 (3)资料用百分数表示的拟合度检验 如果收集到的频数资料已经转成百分数, 这时拟合度检验的方法与上述几种情况基本相 同,只是最后将计算的卡方值乘以 N/100(N 表示总体数)后再查卡方表。 以下就情况(1)我们再看一个例子。 [例 8-2 ]随机抽取了 2000 年 1 月出生的男婴 50 名,分别测出他们的体重,并算出样 本均值为 x =3160g,未修正样本方差为 2 0 s =465.5 2。按体重分组如表 8-6,试以这些观察数 据判断新生男婴的体重是否服从正态分布(显著性水平α=0.05)。 表 8-6 新生男婴体重调查结果 体重分组(g) 组中值M i 频数 0 f 3 700 以上 3 450~3 700 3 200~3 450 2 950~3 200 2 700~2 950 2 450~2 700 2 450 以下 3 825 3 575 3 325 3 075 2 825 2 575 2 325 3 11 10 12 7 5 2 解:由题意我们得出原假设和备选假设如下: H0:新生男婴的体重符合正态分布 H1:新生男婴的体重不符合正态分布 在原假设条件成立的前提下,即符合正态分布,那么mˆ = x , 2 0 2 sˆ = s 。按如下步骤计 算: (1)求各组组中值M i 和平均数 x 的离差 Xi ,即 X M x i = i - ; (2)求各离差的标准分值 0 0 Z X / s (M x )/ s i = i = i - ,i =1,2,.,6; (3)由分值计算 ( ) F 0 Zi ,i =1,2,.,6。并且假定 ( ) 0 F0 Z 0 = , ( ) 1 F0 Z 7 = ; (4)计算 i p = ( ) F 0 Zi - ( ) F0 Z i - 1 , i =1,2,.,7。从而进一步得到 e i f = N ¥ p ;
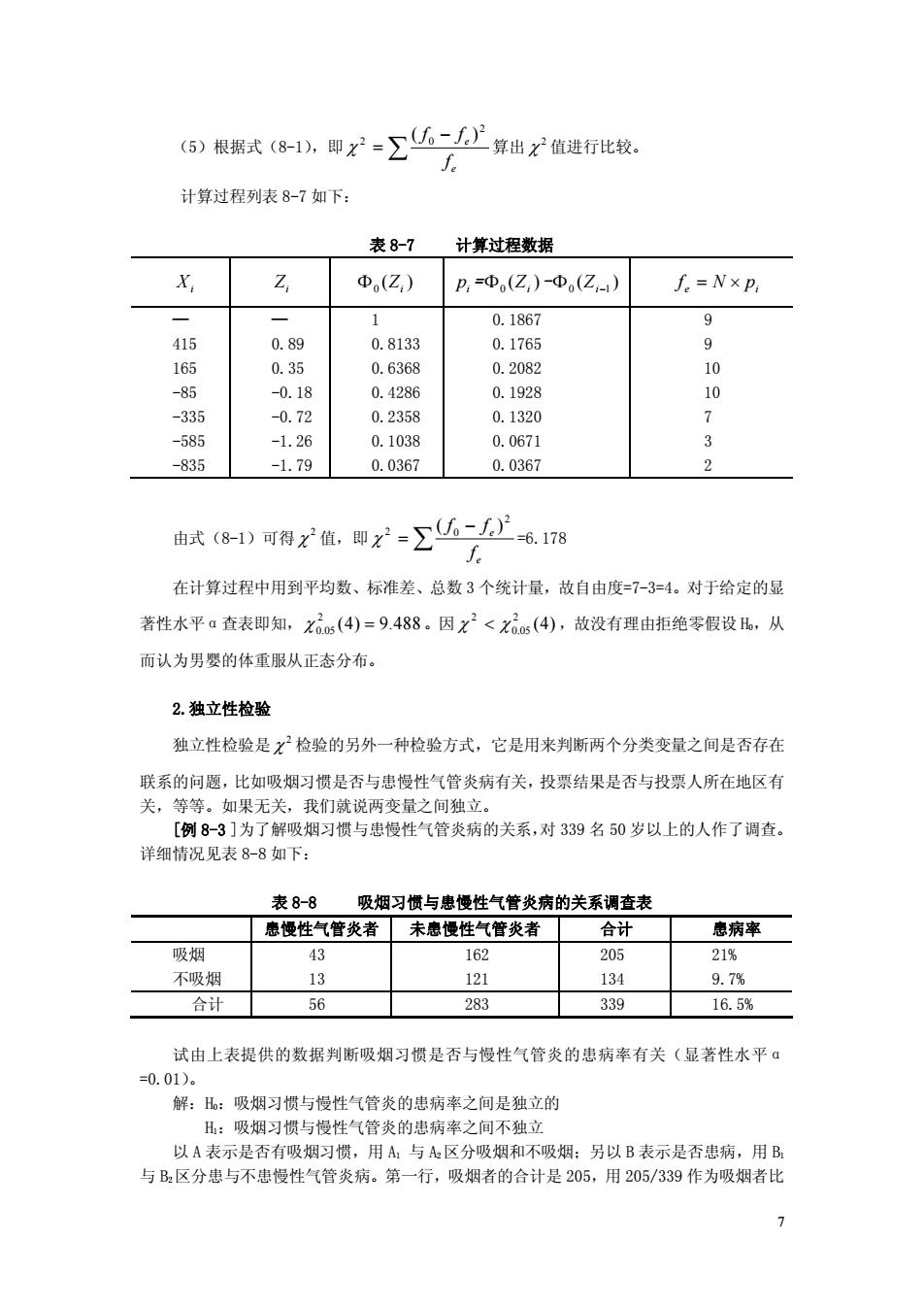
(5)根据式(8-1)即x=∑6-八算出值进行比较。 计算过程列表8-7如下 表8-7 计算过程数据 X, Z Φ(Z) p,=Φ(Z,)-中(Z) f=NxP 0.1867 9 415 0.89 0.8133 0.1765 9 165 0.35 0.6368 0.2082 10 -0.18 0.4286 0.1928 0 0.2358 0.1320 0.1038 0.067 -835 -1.79 0.0367 0.0367 2 式(8=1)可得父值,即x-∑6.178 f 在计算过程中用到平均数、标准差、总数3个统计量,故自由度=7-3=4。对于给定的显 著性水平a查表即知,xs(4)=9.488。因x2<xs(4),故没有理由拒绝零假设,从 而认为男婴的体重服从正态分布。 2.独立性检验 独立性检验是x检验的另外一种检验方式,它是用来判断两个分类变量之间是否存在 联系的问题,比如吸烟习惯是否与患慢性气管炎病有关,投票结果是否与投票人所在地区有 关, 果无关 我们就说两变量之间独立 [例8-3]为了解吸烟习惯与志慢性气管炎病的关系,对339名50岁以上的人作了调查。 详细情况见表8-8如下: 表8-8 吸烟习惯与电梅性气管炎病的关系调杏表 患慢性气管炎者未患慢性气管炎者合计 患病率 吸烟 43 162 205 21% 不吸烟 13 121 134 q7% 合计 56 283 339 16.5% 试由上表提供的数据判断吸烟习惯是否与慢性气管炎的患病率有关(显著性水平α =0.01)。 解::吸烟习惯与慢性气管炎的患病率之间是独立的 H:吸烟习惯与慢性气管炎的惠病率之间不独立 以A表示是否有吸烟习惯,用A与A区分吸烟和不吸烟:另以B表示是否患病,用B 与B,区分患与不患慢性气管炎病。第一行,吸烟者的合计是205,用205/339作为吸烟者比 7
7 (5)根据式(8-1),即 Â - = e e f f f 2 2 0 ( ) c 算出 2 c 值进行比较。 计算过程列表 8-7 如下: 表 8-7 计算过程数据 Xi Zi ( ) F0 Zi i p = ( ) F 0 Zi - ( ) F0 Z i - 1 e i f = N ¥ p — 415 165 -85 -335 -585 -835 — 0.89 0.35 -0.18 -0.72 -1.26 -1.79 1 0.8133 0.6368 0.4286 0.2358 0.1038 0.0367 0.1867 0.1765 0.2082 0.1928 0.1320 0.0671 0.0367 9 9 10 10 7 3 2 由式(8-1)可得 2 c 值,即 Â - = e e f f f 2 2 0 ( ) c =6.178 在计算过程中用到平均数、标准差、总数 3 个统计量,故自由度=7-3=4。对于给定的显 著性水平α查表即知, (4) 9. 488 2 c 0. 05 = 。因 (4) 2 0. 05 2 c < c ,故没有理由拒绝零假设 H0,从 而认为男婴的体重服从正态分布。 2.独立性检验 独立性检验是 2 c 检验的另外一种检验方式,它是用来判断两个分类变量之间是否存在 联系的问题, 比如吸烟习惯是否与患慢性气管炎病有关,投票结果是否与投票人所在地区有 关,等等。如果无关,我们就说两变量之间独立。 [例 8-3 ]为了解吸烟习惯与患慢性气管炎病的关系, 对 339 名 50 岁以上的人作了调查。 详细情况见表 8-8 如下: 表 8-8 吸烟习惯与患慢性气管炎病的关系调查表 患慢性气管炎者 未患慢性气管炎者 合计 患病率 吸烟 不吸烟 43 13 162 121 205 134 21% 9.7% 合计 56 283 339 16.5% 试由上表提供的数据判断吸烟习惯是否与慢性气管炎的患病率有关(显著性水平α =0.01)。 解:H0:吸烟习惯与慢性气管炎的患病率之间是独立的 H1:吸烟习惯与慢性气管炎的患病率之间不独立 以 A 表示是否有吸烟习惯,用 A1 与 A2区分吸烟和不吸烟;另以 B 表示是否患病,用 B1 与 B2区分患与不患慢性气管炎病。第一行,吸烟者的合计是 205,用 205/339 作为吸烟者比

例的估计值,而第一列的合计是56,用56/339作为患慢性气管炎者比例的估计值。如果两 变量间是独立的,那么由独立性的概率乘法公式,有 P(第一单元)=P(AB) =P(A)-P (B) =(205/339)(56/339) =-0.09989 所以可求得第一单元的期望值为0.09989×339=33.86。由此我们可以用以上思路得出 任一单元频数的期望值: 人=xxn=∠x (8-3) nn n 上式中的厂表示列联表中第i行频数的合计,∫,表示第j列频数的合计,n表示总频 数,也就是样本总量。由表8-8和式8-3,将计算过程列表8-9如下: 表8-9计算过程数据 行 列 6-人 6-)2 -f)1f 43 33.86 9.14 83.54 2.47 1 2 162 171.14 -9.14 83.54 0.49 13 9214 -9.14 83.54 377 121 111.86 9.14 83.54 0.75 x-Σ6-八.48 自由度为(r-1)(c-1)=1,对给定的显著性水平a=0.01,查表可知,X()=6.635, 由于x2>X,故拒绝原假设,即认为慢性气管炎的患病率与吸烟无关。 8.3列联表中的相关系数测量 经过前面的内容我们已经了解如何利用父值对列联表中变量之间的相互关系进行检 验。如果变量相互独立,说明它们之间没有联系:反之,则认为它们之间存在联系。而如果 检验变量间存在联系后,我们就会问:它们之间的相关程度有多大:用什么方法来测定变量 之间的相关程度。这里我们就要用到相关系数。 对两变量之间相关程度的测定,主要用相关系数表示。列联表中的变量是类别变量,这 类变量之间的相关关系我们称为品质相关。一般我们用到的品质相关系数有以下三种。 8.3.1p相关系数 口相关系数是描述2×2列联表数据相关程度最常用的一种相关系数。计算公式如下:
8 例的估计值,而第一列的合计是 56,用 56/339 作为患慢性气管炎者比例的估计值。如果两 变量间是独立的,那么由独立性的概率乘法公式,有 P(第一单元)=P(A•B) =P(A) •P(B) =(205/339)(56/339) =0.09989 所以可求得第一单元的期望值为 0.09989×339=33.86。由此我们可以用以上思路得出 任一单元频数的期望值: n f f n n f n f f j i j i e . . . . ¥ = ¥ ¥ = (8-3) 上式中的 i . f 表示列联表中第 i 行频数的合计, j f . 表示第 j 列频数的合计,n 表示总频 数,也就是样本总量。由表 8-8 和式 8-3,将计算过程列表 8-9 如下: 表 8-9 计算过程数据 行 列 0 f e f e f - f 0 2 0 ( ) e f - f 2 0 ( ) e f - f / e f 1 1 2 2 1 2 1 2 43 162 13 121 33.86 171.14 22.14 111.86 9.14 -9.14 -9.14 9.14 83.54 83.54 83.54 83.54 2.47 0.49 3.77 0.75 Â - = e e f f f 2 2 0 ( ) c =7.48 自由度为(r-1)(c-1)=1,对给定的显著性水平α=0.01,查表可知, (1) 6. 635 2 c 0. 1 = , 由于 2 2 c > c a ,故拒绝原假设,即认为慢性气管炎的患病率与吸烟无关。 8.3 列联表中的相关系数测量 经过前面的内容我们已经了解如何利用 2 c 值对列联表中变量之间的相互关系进行检 验。如果变量相互独立,说明它们之间没有联系;反之,则认为它们之间存在联系。而如果 检验变量间存在联系后,我们就会问:它们之间的相关程度有多大;用什么方法来测定变量 之间的相关程度。这里我们就要用到相关系数。 对两变量之间相关程度的测定,主要用相关系数表示。列联表中的变量是类别变量,这 类变量之间的相关关系我们称为品质相关。一般我们用到的品质相关系数有以下三种。 8.3.1 j 相关系数 j 相关系数是描述 2×2 列联表数据相关程度最常用的一种相关系数。计算公式如下:

p=√x21n (8-4) 式中,x即为按式(8-1)计算所得的x2值:n为列联表中的总频数。下边我们就 个一般形式的2×2列联表进行Q相关系数的分析。 表8-102×2列联表 X 合计 为 o a+b c d c+d 合计 a+c b+d 表8-10中,X、Y分别为两变量,a、b、c、d均为条件频数。由公式(8-3)知,每个 单元的频数的期望值为: en=(a+byatc) es=(atcXc+d) ep =(a+bY(b+d) ez =(b+dXc+d) 由公式(8-1),有 =a-en)(-epce)(d-e) eu en e e22 nad-bc) -(a+b)(c+dXa+cXb+d) 由式(8-4)求口相关系数,得 p=Z1n=a+bc+aa+ob+西 ad -bc (8-5) 由式(8-5)可以看出,当ad=bc时,表示变量X、Y之间相互独立,这时p=0。若b=0, c=0时,由式(8-5)计算得=1,这时X和Y之间完全相关。同样,若a0,d=0时,p=-1, 这是X和Y完全相关的另一种情况。因为在列联表中变量的位置可以变换,所以口的符号没 有实际意义,因此当阿=1时表示变量X和Y完全相关:反过来说如果变最X和Y完全相关, 则必定列联表的某个方向对角线的值全为零。 之以说 相关 数是描述2 <2列联表数据相关程度最常用的一种相关系数,是因为 对于2×2列联表,两变量的相关系数绝对值取值范围是在0~1之间,而且若的绝对 值越大说明变量X和Y之间的相关程度越高。 但是,当列联表的行数或者是列数大于2时,?相关系数会随者行数或列数的变大而增 大,并且此时口值会变得没有上限,因此凭印值的大小我们不能说明两个变量间相关程度 的大小,这时可以采用列联相关系数。 9
9 / n 2 j = c (8-4) 式中, 2 c 即为按式(8-1)计算所得的 2 c 值;n 为列联表中的总频数。下边我们就一 个一般形式的 2×2 列联表进行j 相关系数的分析。 表 8-10 2×2 列联表 Y X x1 x2 合计 y1 y2 a b c d a + b c + d 合计 a + c b + d 表 8-10 中,X、Y 分别为两变量,a、b、c、d 均为条件频数。由公式(8-3)知,每个 单元的频数的期望值为: n a b a c e ( )( ) 11 + + = n a c c d e ( )( ) 21 + + = n a b b d e ( )( ) 12 + + = n b d c d e ( )( ) 22 + + = 由公式(8-1),有 22 2 22 21 2 21 12 2 12 11 2 2 11 ( ) ( ) ( ) ( ) e d e e c e e b e e a e - + - + - + - c = ( )( )( )( ) ( ) 2 a b c d a c b d n ad bc + + + + - = 由式(8-4)求j 相关系数,得 ( )( )( )( ) / 2 a b c d a c b d ad bc n + + + + - j = c = (8-5) 由式 (8-5) 可以看出, 当ad = bc 时, 表示变量 X、 Y 之间相互独立, 这时j =0。 若b =0, c =0 时, 由式 (8-5) 计算得j =1, 这时 X 和 Y 之间完全相关。 同样, 若a =0,d =0 时,j =-1, 这是 X 和 Y 完全相关的另一种情况。 因为在列联表中变量的位置可以变换, 所以j 的符号没 有实际意义。 因此当 j = 1时表示变量 X 和 Y 完全相关; 反过来说如果变量 X 和 Y 完全相关, 则必定列联表的某个方向对角线的值全为零。 之所以说j 相关系数是描述 2×2 列联表数据相关程度最常用的一种相关系数,是因为 对于 2×2 列联表,两变量的j 相关系数绝对值取值范围是在 0~1 之间,而且若j 的绝对 值越大说明变量 X 和 Y 之间的相关程度越高。 但是, 当列联表的行数或者是列数大于 2 时,j 相关系数会随着行数或列数的变大而增 大,并且此时j 值会变得没有上限,因此凭j 值的大小我们不能说明两个变量间相关程度 的大小,这时可以采用列联相关系数

8.3.2列联相关系数 列联相关系数是皮尔逊(Pearsor)首创的,因此也叫皮尔逊列联系数或C系数。它是 对口相关系数的改进,主要用于大于2×2列联表,计算 式为: C= (86) Vz2+n 当列联表中两个变量相互独立时,C-0。若两个变量存在相关,则C值随r、C的变大而 增大,但它水远小于1,当两个变量完全相关时,对于2×2列联表,C-0.7071:对于3×3 列联表,C=0.8165:而对于4×4列联表,C-0.87。因此可以用C值的大小米测定两变量的 相关程度。而列联相关系数的局限性在于不适于列联表之间的比较,除非两个列联表的行数 和列数都一致。 8.3.3V相关系数 鉴于p相关系数无上限,C系数小于1的情况,克莱默(Gramer)提出了V相关系数。 它的计算公式是: V= (8-7) Vn×mim(r-),(c-J 它的计算也是以x2值为基础。式中的mi(r-),(c-表示(r-),(c-)中较小 的一个。当两变量完全独立时,V=0:当两变量完全相关时,V=1。所以V的取值在0~1之 间。特别的,如果列联表中有一维为2,即mi[(r-1),(c-1)]=1,则V值就等于o值。 83.4应用举例 我们就以前面例8-3中的数据为例,来分别计算相关系数、列联相关系数、V相关系 数。 由例8-3,我们已求出x2值=7.48,列联表的总频数为n=339。由于是2×2列联表, 所以minl(r-),(c-1l。于是 0=221n-,248 V339 =0.149 7.48 Y7+n1748+39=0.147 7.48 对于相关系数而言,因为当r=2,c=2时,值最大值为1,相比之下,例9-3 中的0=0.183不能认为很大:对于列联相关系数而言,C值必定小于p值,对于3×3列 联表,C的最大值为0.8165,此时C值=0.147,也不能认为很大:对于V而言,V=0.149
10 8.3.2 列联相关系数 列联相关系数是皮尔逊(Pearson)首创的,因此也叫皮尔逊列联系数或 C 系数。它是 对j 相关系数的改进,主要用于大于 2×2 列联表,计算公式为: n C + = 2 2 c c (8-6) 当列联表中两个变量相互独立时,C=0。若两个变量存在相关,则 C 值随 r、c 的变大而 增大,但它永远小于 1,当两个变量完全相关时,对于 2×2 列联表,C=0.7071;对于 3×3 列联表,C=0.8165;而对于 4×4 列联表,C=0.87。因此可以用 C 值的大小来测定两变量的 相关程度。而列联相关系数的局限性在于不适于列联表之间的比较,除非两个列联表的行数 和列数都一致。 8.3.3 V 相关系数 鉴于j 相关系数无上限,C 系数小于 1 的情况,克莱默(Gramer)提出了 V 相关系数。 它的计算公式是: min[( 1), ( 1)] 2 ¥ - - = n r c V c (8-7) 它的计算也是以 2 c 值为基础。式中的 min[(r -1 ),(c -1 )]表示(r -1 ) ,(c -1 ) 中较小 的一个。当两变量完全独立时,V=0;当两变量完全相关时,V=1。所以 V 的取值在 0~1 之 间。特别的,如果列联表中有一维为 2,即min[(r -1 ),(c -1 )]=1,则 V 值就等于j 值。 8.3.4 应用举例 我们就以前面例 8-3 中的数据为例,来分别计算j 相关系数、列联相关系数、V 相关系 数。 由例 8-3,我们已求出 2 c 值=7.48,列联表的总频数为n =339。由于是 2×2 列联表, 所以min[(r -1 ),(c -1 )]=1。于是 0 .149 339 7 .48 / 2 j = c n = = 0 .147 7 .48 339 7 .48 2 2 = + = + = n C c c 0. 149 339 1 7. 48 min[( 1), ( 1)] 2 = ¥ = ¥ - - = n r c V c 对于j 相关系数而言,因为当r = 2 , c = 2 时,j 值最大值为 1 ,相比之下,例 9-3 中的j = 0.183 不能认为很大;对于列联相关系数而言,C 值必定小于j 值,对于 3×3 列 联表,C 的最大值为 0.8165 ,此时 C 值=0.147,也不能认为很大;对于 V 而言,V=0.149