
第六章 直线回归与相关 客观事物在发展过程中是相互联系、相 互影响,常常要研究两个或两个以上变 量间的关系。 上一张 下一张 主 页 退 出
第六章 直线回归与相关 客观事物在发展过程中是相互联系、相 互影响,常常要研究两个或两个以上变 量间的关系。 上一张 下一张 主 页 退 出

上一张 下一张 主 页 退 出 1 回归与相关的概念 一类是完全确定性的关系,又称函数关系,可以 用精确的数学表达式来表示,即当变量x的值取 定后,变量y有唯一确定的值与之对应。 如长方形的面积(S) 与 长(a)和宽(b)的关 系: S=ab。它们之间的关系是确定性的,只要 知道了其中两个变量的值就可以精确地计算出另一 个变量的值,这类变量间的关系称为函数关系。 各种变量间的关系大致可分为两类: 确定性关系 非确定性关系
上一张 下一张 主 页 退 出 1 回归与相关的概念 一类是完全确定性的关系,又称函数关系,可以 用精确的数学表达式来表示,即当变量x的值取 定后,变量y有唯一确定的值与之对应。 如长方形的面积(S) 与 长(a)和宽(b)的关 系: S=ab。它们之间的关系是确定性的,只要 知道了其中两个变量的值就可以精确地计算出另一 个变量的值,这类变量间的关系称为函数关系。 各种变量间的关系大致可分为两类: 确定性关系 非确定性关系

如人的身高与体重的关系,作物种植密度与产量的关 系,食品价格与需求量的关系等等,这些变量间都存在着 十分密切的关系,但不能由一个或几个变量的值精确地求 出另一个变量的值。统计学中把这些变量间的关系称为相 关关系,把存在相关关系的变量称为相关变量。 上一张 下一张 主 页 退 出 另一类是 非确定性关系,不能用精确的数学公 式来表示,当变量x的值取定后,y有若干种可 能取值。 在一定范围内,对一个变量的任意数值(Xi), 虽然没有另一个变量的确定数值yi与之对应,但是却有 一个特定yi的条件概率分布与之对应,这种变量的不确 定关系,称为相关关系
如人的身高与体重的关系,作物种植密度与产量的关 系,食品价格与需求量的关系等等,这些变量间都存在着 十分密切的关系,但不能由一个或几个变量的值精确地求 出另一个变量的值。统计学中把这些变量间的关系称为相 关关系,把存在相关关系的变量称为相关变量。 上一张 下一张 主 页 退 出 另一类是 非确定性关系,不能用精确的数学公 式来表示,当变量x的值取定后,y有若干种可 能取值。 在一定范围内,对一个变量的任意数值(Xi), 虽然没有另一个变量的确定数值yi与之对应,但是却有 一个特定yi的条件概率分布与之对应,这种变量的不确 定关系,称为相关关系

一种是因果关系,即一个变量的变 化受另一个或几个变量的影响。如小麦 的生长速度受遗传特性、营养水平、管 理条件等因素的影响。 另一种是平行关系,它们互为因果 或共同受到另外因素的影响。如人的身 高和胸围之间的关系属于平行关系。 上一张 下一张 主 页 退 出 相关变量间的关系一般分为两种:
一种是因果关系,即一个变量的变 化受另一个或几个变量的影响。如小麦 的生长速度受遗传特性、营养水平、管 理条件等因素的影响。 另一种是平行关系,它们互为因果 或共同受到另外因素的影响。如人的身 高和胸围之间的关系属于平行关系。 上一张 下一张 主 页 退 出 相关变量间的关系一般分为两种:

研究“一因一果”,即一个自变量与一个依 变量的回归分析称为一元回归分析; 研究“多因一果”,即多个自变量与一个依 变量的回归分析称为多元回归分析。 一元回归分析又分为直线回归分析与曲线回 归分析两种;多元回归分析又分为多元线性回归 分析与多元非线性回归分析两种。 上一张 下一张 主 页 退 出 统计学上采用回归分析 (regression analysis)方法研究呈因果关系的相关变量间 的关系。表示原因的变量称为自变量,表示结果 的变量称为依变量
研究“一因一果”,即一个自变量与一个依 变量的回归分析称为一元回归分析; 研究“多因一果”,即多个自变量与一个依 变量的回归分析称为多元回归分析。 一元回归分析又分为直线回归分析与曲线回 归分析两种;多元回归分析又分为多元线性回归 分析与多元非线性回归分析两种。 上一张 下一张 主 页 退 出 统计学上采用回归分析 (regression analysis)方法研究呈因果关系的相关变量间 的关系。表示原因的变量称为自变量,表示结果 的变量称为依变量

回归分析的任务就是揭示出呈因果关系 的相关变量间的联系形式,建立它们之 间的回归方程,利用所建立的回归方程, 由自变量(原因)来预测、控制依变量 (结果)。 回归分析主要包括:找出回归方程;检 验回归方程是否显著;通过回归方程来 预测或控制另一变量
回归分析的任务就是揭示出呈因果关系 的相关变量间的联系形式,建立它们之 间的回归方程,利用所建立的回归方程, 由自变量(原因)来预测、控制依变量 (结果)。 回归分析主要包括:找出回归方程;检 验回归方程是否显著;通过回归方程来 预测或控制另一变量

对多个变量进行相关分析时,研究一个 变量与多个变量间的线性相关称为复相关 分析;研究其余变量保持不变的情况下两 个变量间的线性相关称为偏相关分析。 上一张 下一张 主 页 退 出 统计学上采用相关分析 ( correlation analysis)来研究呈平行关系相关变量之间 的关系。 对两个变量间的直线关系进行相关分析 称为简单相关分析(也叫直线相关分析);
对多个变量进行相关分析时,研究一个 变量与多个变量间的线性相关称为复相关 分析;研究其余变量保持不变的情况下两 个变量间的线性相关称为偏相关分析。 上一张 下一张 主 页 退 出 统计学上采用相关分析 ( correlation analysis)来研究呈平行关系相关变量之间 的关系。 对两个变量间的直线关系进行相关分析 称为简单相关分析(也叫直线相关分析);
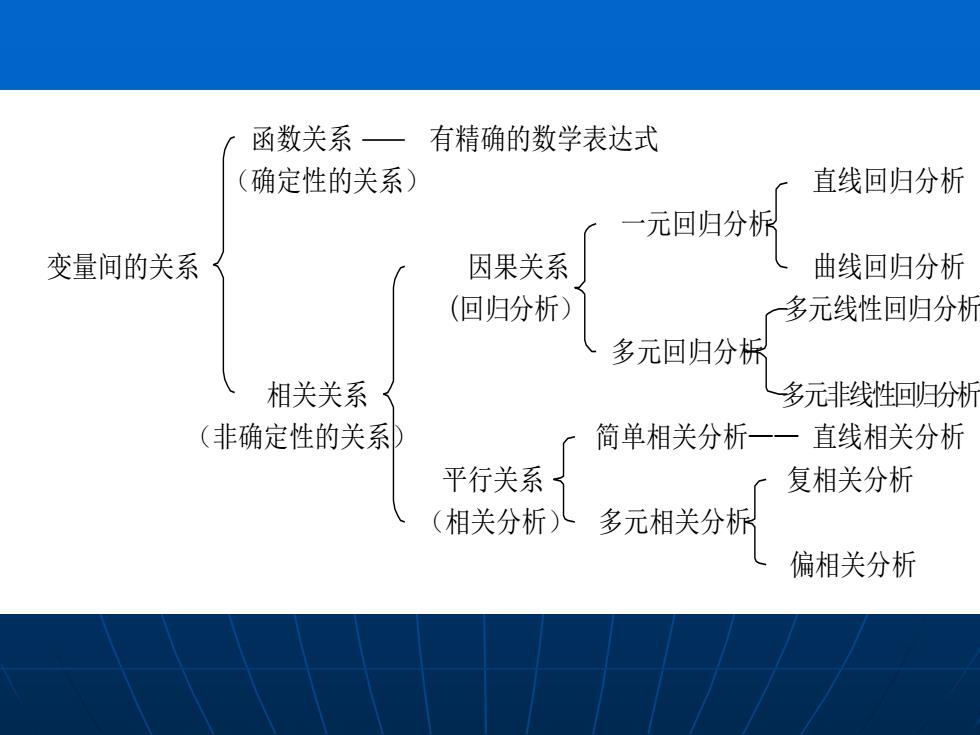
函数关系 有精确的数学表达式 (确定性的关系) 直线回归分析 一元回归分析 变量间的关系 因果关系 曲线回归分析 (回归分析) 多元线性回归分析 多元回归分析 相关关系 多元非线性回归分析 (非确定性的关系) 简单相关分析—— 直线相关分析 平行关系 复相关分析 (相关分析) 多元相关分析 偏相关分析
函数关系 有精确的数学表达式 (确定性的关系) 直线回归分析 一元回归分析 变量间的关系 因果关系 曲线回归分析 (回归分析) 多元线性回归分析 多元回归分析 相关关系 多元非线性回归分析 (非确定性的关系) 简单相关分析—— 直线相关分析 平行关系 复相关分析 (相关分析) 多元相关分析 偏相关分析

2 直线回归 2.1 直线回归方程的建立 上一张 下一张 主 页 退 出 为了直观地看出x和y间的变化趋势,可将 每一对观测值在平面直角坐标系中描点,作出散 点图 (见图6-1)。 2.1.1数学模型 对于两个相关变量,一个变量用x表示,另 一个变量用y表示,如果通过试验或调查获得两 个变量的n对观测值:(x1,y1),(x2, y2),.,(xn,yn)
2 直线回归 2.1 直线回归方程的建立 上一张 下一张 主 页 退 出 为了直观地看出x和y间的变化趋势,可将 每一对观测值在平面直角坐标系中描点,作出散 点图 (见图6-1)。 2.1.1数学模型 对于两个相关变量,一个变量用x表示,另 一个变量用y表示,如果通过试验或调查获得两 个变量的n对观测值:(x1,y1),(x2, y2),.,(xn,yn)
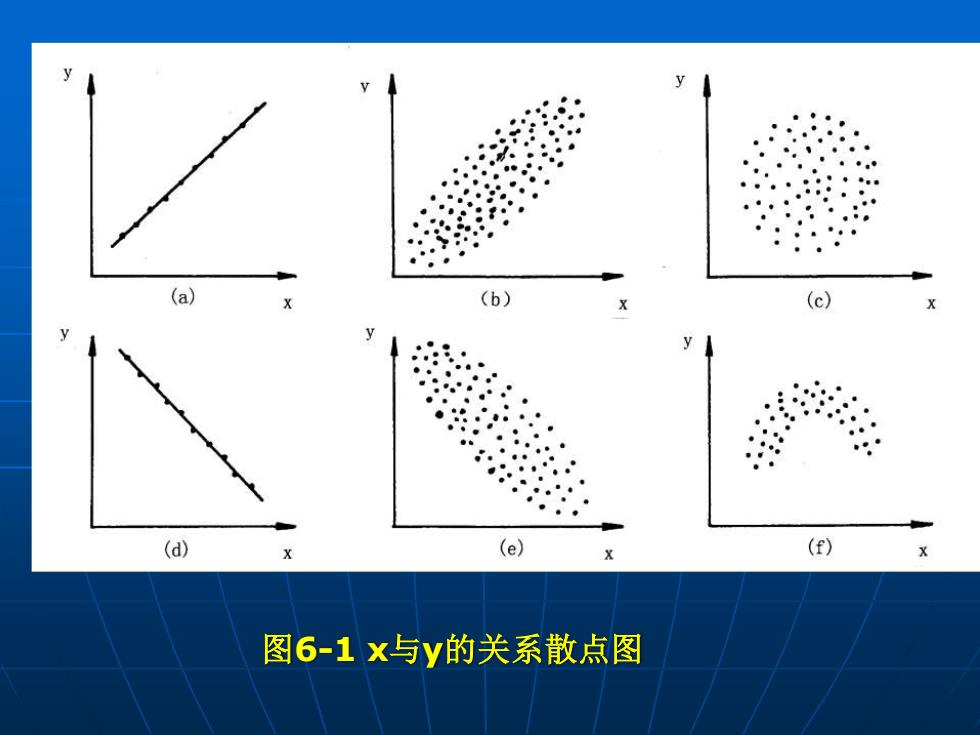
图6-1 x与y的关系散点图
图6-1 x与y的关系散点图