
抽样分布 参数估计简介 假设检验的基本原理 统计推断概述
抽样分布 参数估计简介 假设检验的基本原理 统计推断概述

抽样分布的概念 样本统计量的概率分布称为抽样分布 (sampling distribution) ➢ 样本是通过对总体的随机抽样获得的 ➢ 样本统计量是随机变量,有一定的概率分布 简单随机样本 ➢抽样是完全随机的- 总体中的每个个体都 有相同的机会被抽中 ➢抽样是彼此对立的- 每次抽样的结果都不 会影响到其他抽样的结果
抽样分布的概念 样本统计量的概率分布称为抽样分布 (sampling distribution) ➢ 样本是通过对总体的随机抽样获得的 ➢ 样本统计量是随机变量,有一定的概率分布 简单随机样本 ➢抽样是完全随机的- 总体中的每个个体都 有相同的机会被抽中 ➢抽样是彼此对立的- 每次抽样的结果都不 会影响到其他抽样的结果
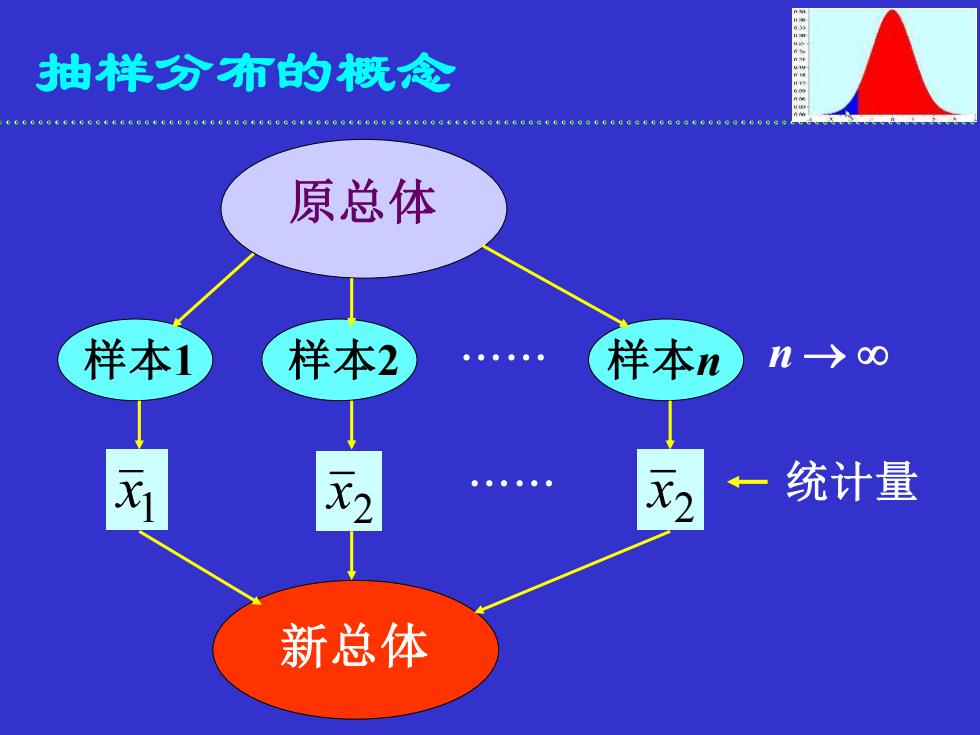
抽样分布的概念 原总体 样本1 样本2 样本n 1 x 2 x 2 x 新总体 n → 统计量
抽样分布的概念 原总体 样本1 样本2 样本n 1 x 2 x 2 x 新总体 n → 统计量

2 (chi-square)分布 定义 ➢设随机变量X1, X2, , Xn彼此独立且都服从 标准正态分布 N(0, 1),则随机变量 = 2 Y Xi 服从自由度为n的 2分布,记为 ~ ( ) 2 Y n
2 (chi-square)分布 定义 ➢设随机变量X1, X2, , Xn彼此独立且都服从 标准正态分布 N(0, 1),则随机变量 = 2 Y Xi 服从自由度为n的 2分布,记为 ~ ( ) 2 Y n
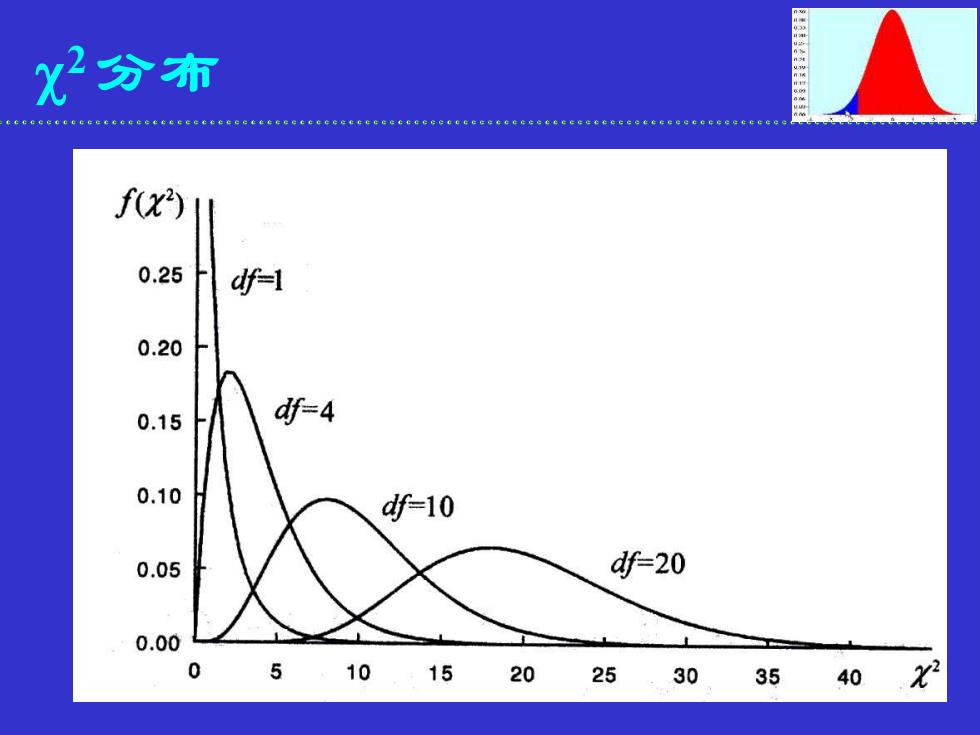
2 分布
2 分布

2 分布 性质 ➢ 2 分布随机变量的取值范围为(0,) ➢若Y1 ~ 2 (n),Y2 ~ 2 (m),且相互独立,则 • Y1 ± Y2 ~ 2 (n ± m) ➢ 2 分布为非对称分布,其分布曲线的形状由 自由度决定,自由度越大,分布越趋于对称 ➢当 n → , 2 (n) → N(n, 2n)
2 分布 性质 ➢ 2 分布随机变量的取值范围为(0,) ➢若Y1 ~ 2 (n),Y2 ~ 2 (m),且相互独立,则 • Y1 ± Y2 ~ 2 (n ± m) ➢ 2 分布为非对称分布,其分布曲线的形状由 自由度决定,自由度越大,分布越趋于对称 ➢当 n → , 2 (n) → N(n, 2n)
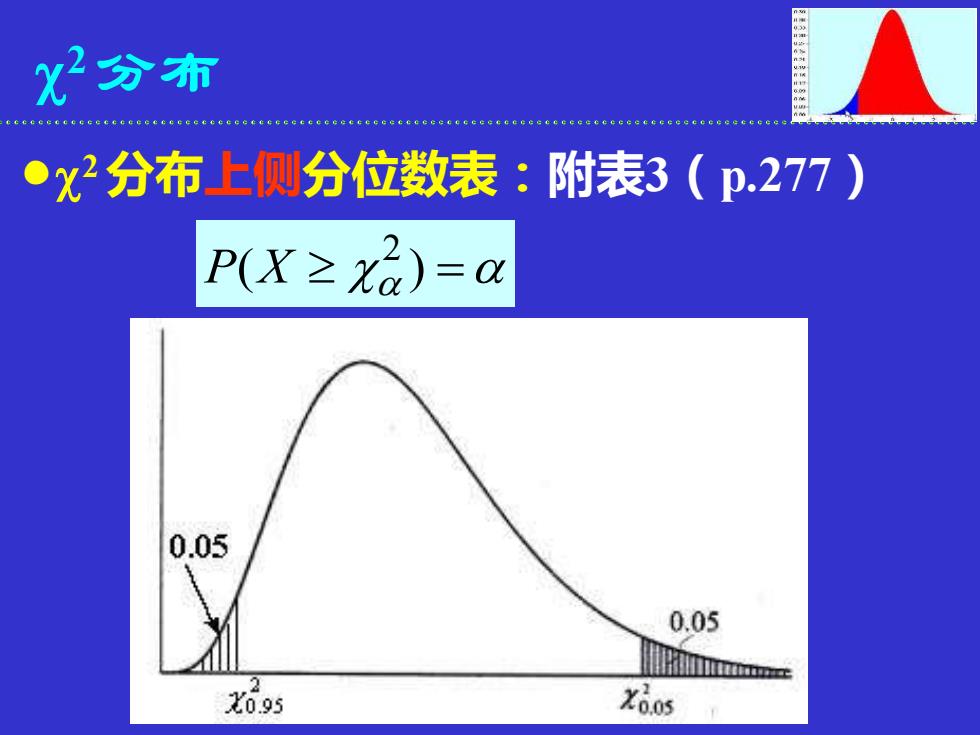
2 分布 2 分布上侧分位数表:附表3(p.277) ( ) = 2 P X
2 分布 2 分布上侧分位数表:附表3(p.277) ( ) = 2 P X
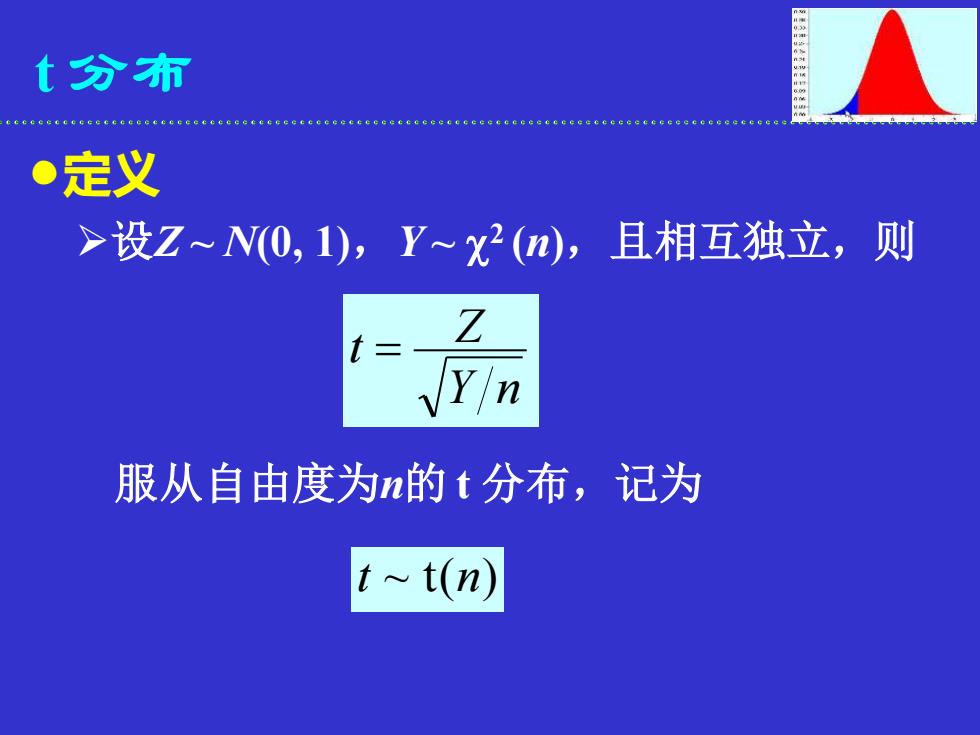
t 分布 定义 ➢设Z ~ N(0, 1),Y ~ 2 (n),且相互独立,则 Y n Z t = 服从自由度为n的 t 分布,记为 t ~ t(n)
t 分布 定义 ➢设Z ~ N(0, 1),Y ~ 2 (n),且相互独立,则 Y n Z t = 服从自由度为n的 t 分布,记为 t ~ t(n)
t 分布
t 分布

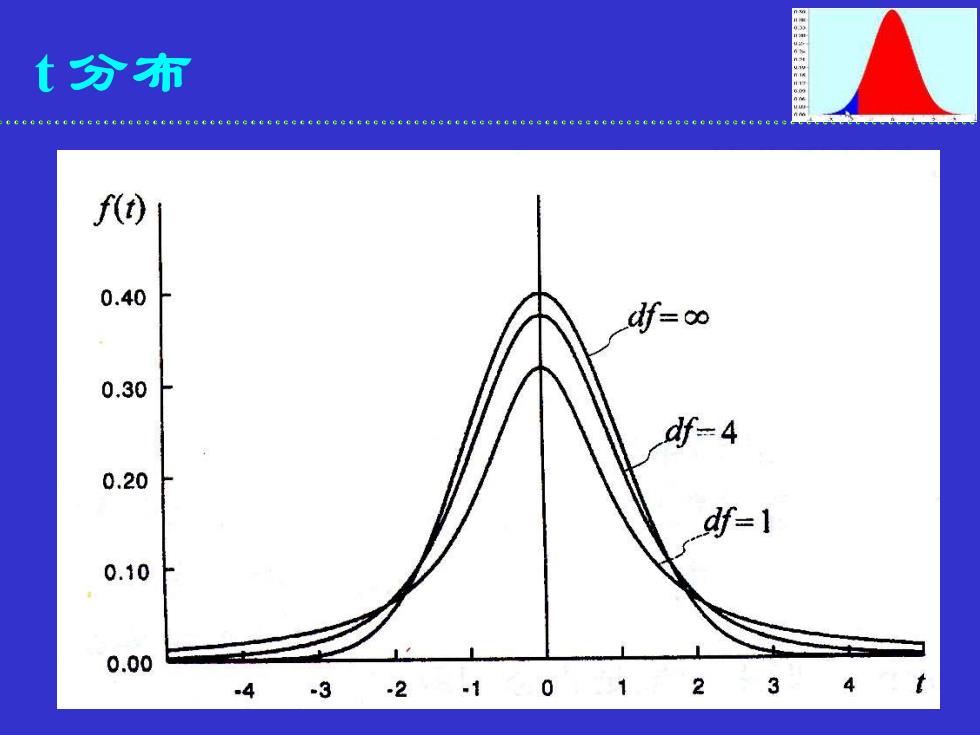
t 分布 性质 ➢与标准正态分布相似 • 关于 t = 0对称 • 只有一个峰,峰值在t = 0 ➢分布曲线受自由度影响,自由度越小,离散 程度越大 ➢当 n → ,t(n) → N(0, 1)
t 分布 性质 ➢与标准正态分布相似 • 关于 t = 0对称 • 只有一个峰,峰值在t = 0 ➢分布曲线受自由度影响,自由度越小,离散 程度越大 ➢当 n → ,t(n) → N(0, 1)