
第二节单向分组资料的方差分析 1、组内观察值数目相等的单向分组资料的方差分析 2、组内观察值数目不等的单向分组资料的方差分析 3、组内又分亚组的单向分组资料的方差分析
第二节 单向分组资料的方差分析 1、组内观察值数目相等的单向分组资料的方差分析 2、组内观察值数目不等的单向分组资料的方差分析 3、组内又分亚组的单向分组资料的方差分析
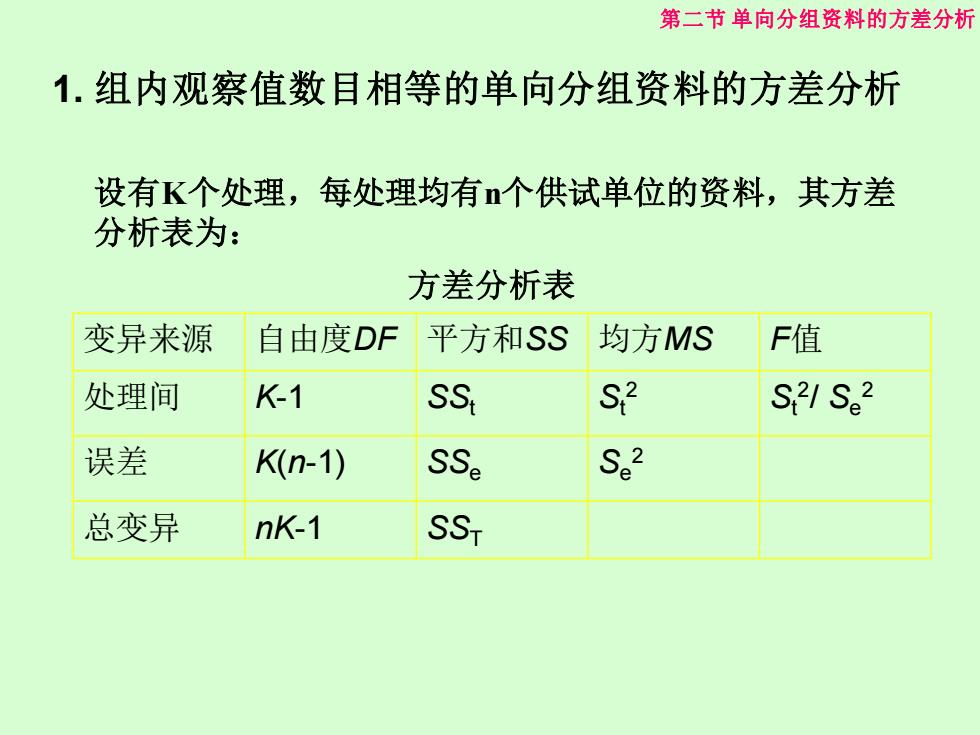
第二节单向分组资料的方差分析 1.组内观察值数目相等的单向分组资料的方差分析 设有K个处理,每处理均有个供试单位的资料,其方差 分析表为: 方差分析表 变异来源 自由度DF 平方和SS 均方MS F值 处理间 K-1 SS S2 S21 S2 误差 K(n-1) SSe S2 总变异 nK-1 SS
设有K个处理,每处理均有n个供试单位的资料,其方差 分析表为: 方差分析表 变异来源 自由度DF 平方和SS 均方MS F值 处理间 K-1 SSt St 2 St 2 / Se 2 误差 K(n-1) SSe Se 2 总变异 nK-1 SST 第二节 单向分组资料的方差分析 1. 组内观察值数目相等的单向分组资料的方差分析
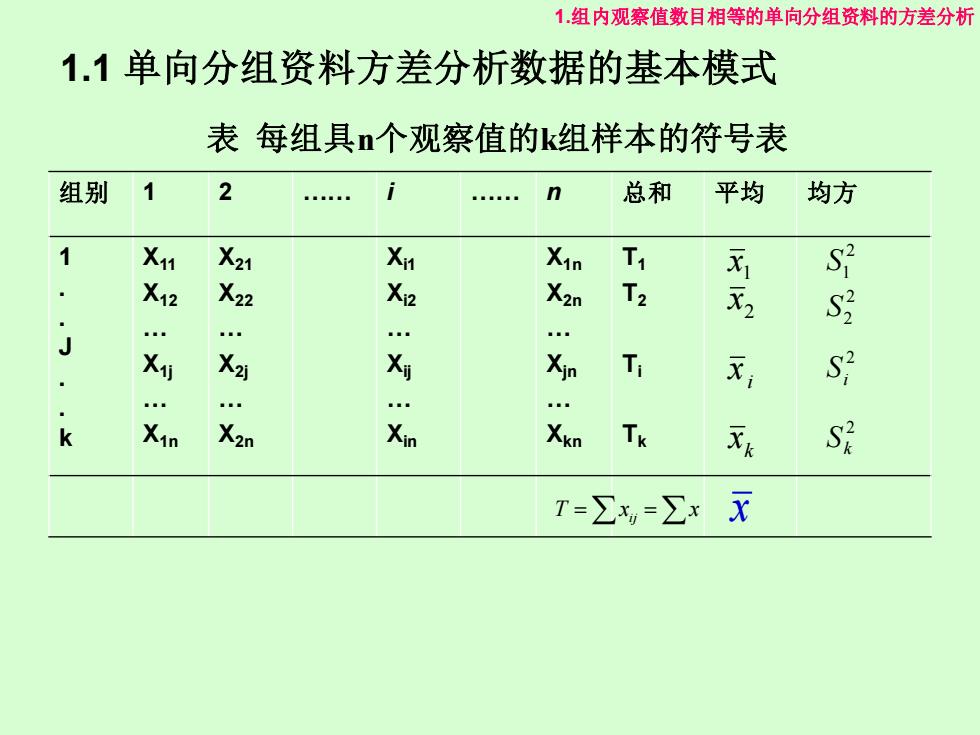
1组内观察值数目相等的单向分组资料的方差分析 1.1单向分组资料方差分析数据的基本模式 表每组具n个观察值的k组样本的符号表 组别 2 总和 平均 均方 X1 X21 Xi Xin X S2 X12 X22 Xi2 X2n T2 X2 S Xi X2j X Xin Ti 灭 S Xin X2n Xin Xin Tk Xk T=∑,=∑xx
1.1 单向分组资料方差分析数据的基本模式 组别 1 2 . i . n 总和 平均 均方 1 . . J . . k X11 X12 . X1j . X1n X21 X22 . X2j . X2n Xi1 Xi2 . Xij . Xin X1n X2n . Xjn . Xkn T1 T2 Ti Tk 1 x 2 x i x k x T =x =x ij x 2 1 S 2 2 S 2 i S 2 k S 表 每组具n个观察值的k组样本的符号表 1.组内观察值数目相等的单向分组资料的方差分析

1组内观察值数目相等的单向分组资料的方差分析 计算公式 上述资料的自由度和平方和的分解式为: 总自由度=组间自由度十组内自由度 (nk-1)=(k-1)+k-1) 总平方和=组间平方和十组内平方和 8,=-列=2民-到+22,-为 s,-22=吃民-+22,-
上述资料的自由度和平方和的分解式为: 总自由度=组间自由度 + 组内自由度 (nk-1)=(k-1)+ k(n-1) 总平方和=组间平方和 + 组内平方和 计算公式 = = = = − = − + − k i n j i j i k i i n k T i j SS x x n x x x x 1 1 2 1 2 1 2 ( ) ( ) [ ( ) ] = = = = = = − = − + − k i n j i j i k i i k i n j T i j SS x x n x x x x 1 1 2 1 2 1 1 2 ( ) ( ) ( ) 1.组内观察值数目相等的单向分组资料的方差分析

1.组内观察值数目相等的单向分组资料的方差分析 总平方和(SS) 总变异是nk个观察值的变异,平方和SS为: 西,=8x-=∑¥∑-z nk nk =C 式中,C称为矫正数。 nk s8,=2-m=∑2-c nk
总变异是nk个观察值的变异,平方和SST为: nk T x nk x SS x x x T 2 2 2 2 2 ( ) ( ) = ( − ) = − = − 式中,C 称为矫正数。 总平方和 (SST ) C nk T = 2 ( ) x C nk T SS x T = − = − 2 2 2 ( ) 1.组内观察值数目相等的单向分组资料的方差分析

1组内观察值数目相等的单向分组资料的方差分析 组间变异即k个平均数的变异,故其自由度为k一1,平方 和SSt为: SS,=n∑(民-x)1 组内的变异为各组内观察值与组平均数的相差,故每组 具有一1个自由度,平方和为∑x,-),而总共有k组资料, 故组内自由度为k(n一1),而组内平方和SSe为: -2这-
组内的变异为各组内观察值与组平均数的相差,故每组 具有n-1个自由度,平方和为 ,而总共有k 组资料, 故组内自由度为k(n-1),而组内平方和SSe为: 2 ( − ) ij i x x t k i T n j SSe xi j xi = SS − SS = − =1 =1 2 ( ) 组间变异即k个平均数的变异,故其自由度为k-1,平方 和 SSt 为: = − 2 SS n (x x) t i 1.组内观察值数目相等的单向分组资料的方差分析
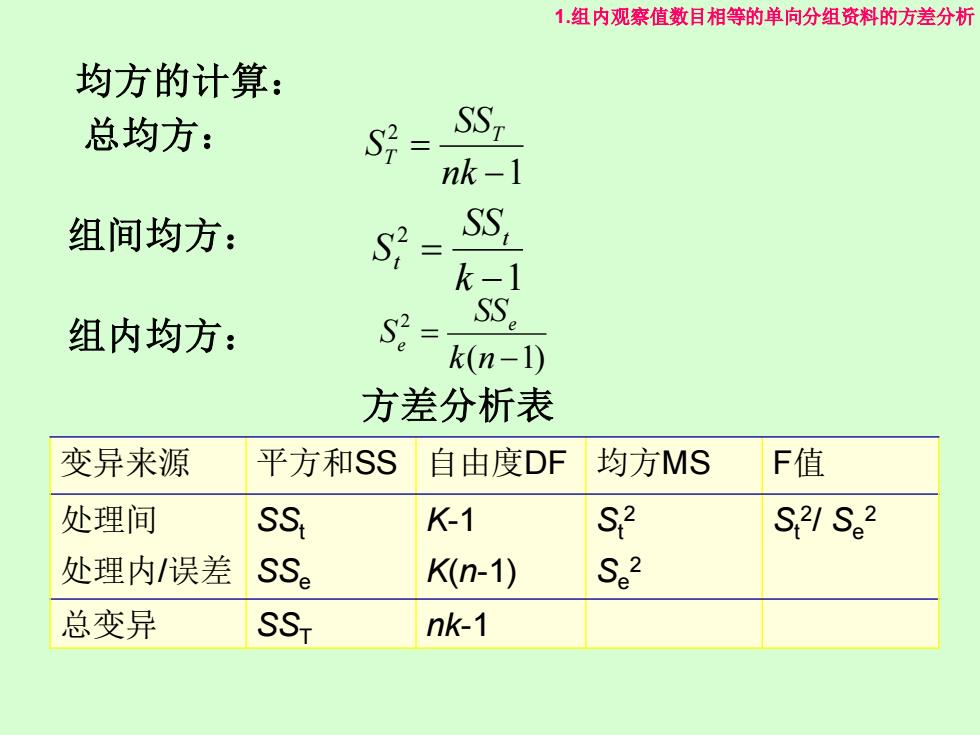
1.组内观察值数目相等的单向分组资料的方差分析 均方的计算: 总均方: 2= SST nk -1 组间均方: SS, k-1 组内均方: S2= SS。 k(n-1) 方差分析表 变异来源 平方和SS 自由度DF 均方MS F值 处理间 SS K-1 S2 S21S。2 处理内/误差 SSe K(n-1) Se2 总变异 SSt nk-1
均方的计算: ( 1) 2 − = k n SS S e e 1 2 − = nk SS S T T 1 2 − = k SS S t t 总均方: 组间均方: 组内均方: 1.组内观察值数目相等的单向分组资料的方差分析 方差分析表 变异来源 平方和SS 自由度DF 均方MS F值 处理间 SSt K-1 St 2 St 2 / Se 2 处理内/误差 SSe K(n-1) Se 2 总变异 SST nk-1
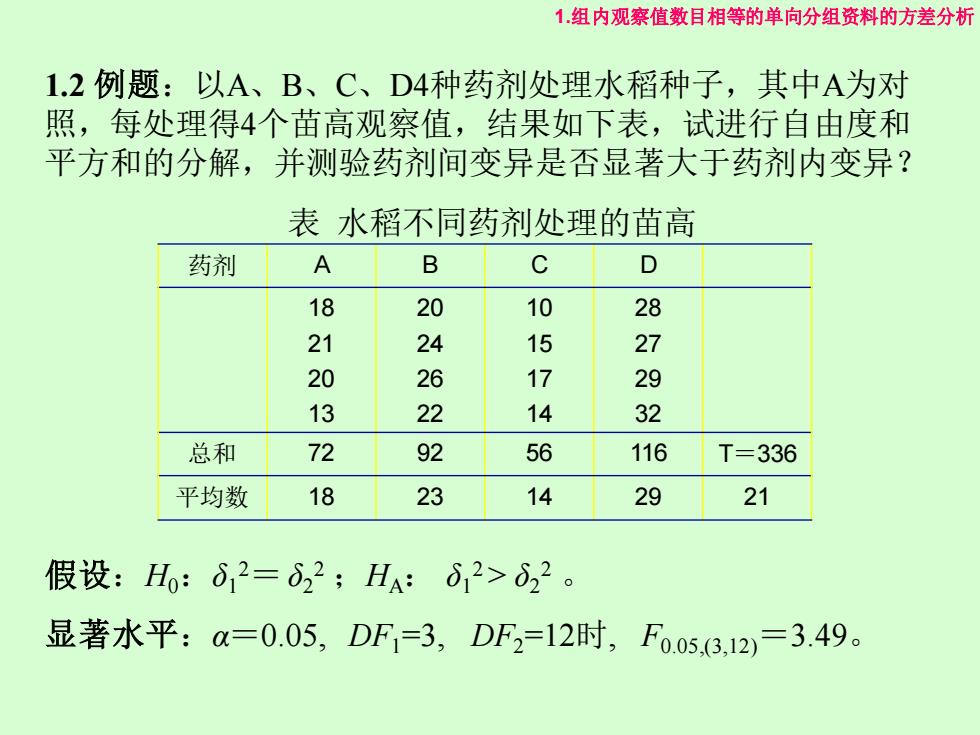
1组内观察值数目相等的单向分组资料的方差分析 1.2例题:以A、B、C、D4种药剂处理水稻种子,其中A为对 照,每处理得4个苗高观察值,结果如下表,试进行自由度和 平方和的分解,并测验药剂间变异是否显著大于药剂内变异? 表水稻不同药剂处理的苗高 药剂 A B c D 18 20 10 28 21 24 15 27 20 26 17 29 13 22 14 32 总和 72 92 56 116 T=336 平均数 18 23 14 29 21 假设:H:62=22;HA:δ2>022。 显著水平:a=0.05,DF=3,DF2=12时,Fo.o53,12=3.49
1.2 例题:以A、B、C、D4种药剂处理水稻种子,其中A为对 照,每处理得4个苗高观察值,结果如下表,试进行自由度和 平方和的分解,并测验药剂间变异是否显著大于药剂内变异? 表 水稻不同药剂处理的苗高 假设:H0:δ1 2=δ2 2 ;HA: δ1 2 > δ2 2 。 显著水平:α=0.05, DF1=3, DF2=12时, F0.05,(3,12) =3.49。 药剂 A B C D 18 21 20 13 20 24 26 22 10 15 17 14 28 27 29 32 总和 72 92 56 116 T=336 平均数 18 23 14 29 21 1.组内观察值数目相等的单向分组资料的方差分析

1.组内观察值数目相等的单向分组资料的方差分析 计算过程: a.分解自由度 总自由度=组间自由度+组内自由度(k-1)=(k1)+k-1) 4×4-1=(4-1)+4(4-1) 15=3+12 b.分解和平方和: 82鸣低矿+别 总平方和-∑-g-2-C8w x2=182+202+212+.+322=623C=336÷16=21 SST=623-21=602 组间平方和SS,=n∑(:,-x)2=∑T2/n-C ∑(722+922+562+1162)÷4-21=504 组内平方和(SSe)=总平方和一组间平方和=602一504=98
a.分解自由度 总自由度=组间自由度 + 组内自由度 (nk-1)=(k-1)+ k(n-1) 4×4-1=(4-1)+4(4-1) 15 = 3 + 12 b.分解和平方和: = = = = − = − + − k i n j ij i k i i nk T ij SS x x n x x x x 1 1 2 1 2 1 2 ( ) ( ) [ ( ) ] = = = = = = − = − + − k i n j ij i k i i k i n j T ij SS x x n x x x x 1 1 2 1 2 1 1 2 ( ) ( ) ( ) x C nk T SS x T = − = − 2 2 2 ( ) 组间平方和 ∑x 2=182+202+212+.+322=623 C=336÷16=21 SST=623-21=602 SSt = n(xi − x) =Ti / n −C 2 2 ∑(722+922+562+1162 )÷4-21=504 组内平方和(SSe)=总平方和-组间平方和=602-504=98 总平方和 计算过程: 1.组内观察值数目相等的单向分组资料的方差分析

1组内观察值数目相等的单向分组资料的方差分析 C.计算均方 总均方 S= SST =602÷15=40.13 nk -1 组间均方S? SS, =504÷3=168.0 k-1 组内均方S2= SS。 =98÷12=8.17 k(n-1)
C.计算均方 1 2 − = nk SS S T T 1 2 − = k SS S t t ( 1) 2 − = k n SS S e e =602÷15=40.13 组间均方 组内均方 总均方 =504÷3=168.0 =98÷12=8.17 1.组内观察值数目相等的单向分组资料的方差分析