
第四节二项资料的百分数假设检验 Test of percent hypothesis ·适用于以百分数或成数表示试验的结果分析。 如病株率、有虫株率、杀虫率、发芽率等。 ·理论上讲,这类资料应按照二项分布进行,但当样本 容量n较大,p不过小,np、ng又均不小于5时, (p+q的分布趋近于正态分布,因而,可将百分数的 资料作正态分布处理
• 适用于以百分数或成数表示试验的结果分析。 如病株率、有虫株率、杀虫率、发芽率等。 • 理论上讲,这类资料应按照二项分布进行,但当样本 容量n较大,p不过小,np、nq又均不小于5时, (p+q) n的分布趋近于正态分布,因而,可将百分数的 资料作正态分布处理。 第四节 二项资料的百分数假设检验 Test of percent hypothesis
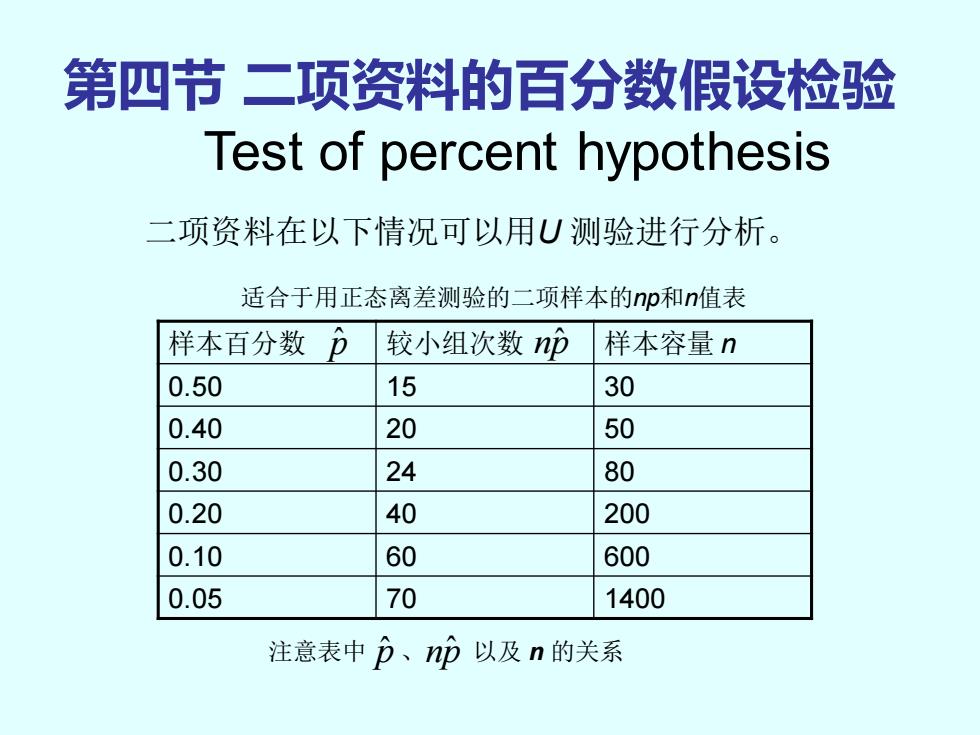
第四节二项资料的百分数假设检验 Test of percent hypothesis 二项资料在以下情况可以用U测验进行分析。 适合于用正态离差测验的二项样本的np和n值表 样本百分数D 较小组次数np 样本容量n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400 注意表中p、np以及n的关系
第四节 二项资料的百分数假设检验 Test of percent hypothesis 二项资料在以下情况可以用U 测验进行分析。 适合于用正态离差测验的二项样本的np和n值表 样本百分数 较小组次数 样本容量 n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400 p ˆ np ˆ 注意表中 p ˆ 、np ˆ 以及 n 的关系

第四节二项资料的百分数假设检验 Test of percent hypothesis 1、单个样本百分数的假设测验 2、两个样本百分数相比较的假设测验 3、二项样本假设测验时的连续矫正
第四节 二项资料的百分数假设检验 Test of percent hypothesis 1、单个样本百分数的假设测验 2、两个样本百分数相比较的假设测验 3、二项样本假设测验时的连续矫正

Test of percent hypothesis 二项总体抽样的分布 二项总体的平均数则=p,方差σ2=p(1-p)=pq 标准差为o=Vp(I-p)=Vpg 样本平均数抽样分布 平均数,4=卫 方差, :=pq n 标准误, 0: =pa-p)
二项总体抽样的分布 二项总体的平均数μ=p,方差σ2 =p(1-p)=p q 标准差为 = p(1− p) = pq 样本平均数抽样分布 平均数, 方差, 标准误, n p p n pq n pq p x x x (1 ) 2 − = = = = Test of percent hypothesis

二项总体的分布参数 ·例:一个总体内有5个个体,分别为0、1、0、1、1。 ·则:W=(0+1+0+1+1)÷5=0.6 ·所以u=p ·σ2=[0-0.6)2+(1-0.6)2++(0-0.6)2]÷5=0.24 区②5-a o=√0.24=0.49 (每次取一个样,即:n=1)
二项总体的分布参数 • 例:一个总体内有5个个体,分别为0、1、0、1、1。 • 则:μ=( 0+1 + 0 + 1 + 1 )÷5=0.6 • 所以μ= p • σ2=[(0-0.6)2+(1-0.6)2+.+(0-0.6)2 ]÷5=0.24 = 0.24 = 0.49 ( ) 5 0.24 5 9 3 2 2 2 = = − = − n n x x (每次取一个样,即: n =1)

Test of percent hypothesis 1、单个样本百分数的假设测验 。 测试百分数B所属总体百分数与某一理论值或期望值P的 差异显著性。 。样本百分数的标准误为: 0=1 故由 u= -Po 例:紫花与白花大豆杂交,在F2代共得到289株,其中紫 花208株,白花81株。如果花色受一对等位基因控制,根 据遗传学原理,F2代紫花与白花分离的比例应为3:1,即 紫花理论数为p=0.75,白花为q=1-p=0.25。问该试验是 否符合一对等位基因的的遗传规律?
1、单个样本百分数的假设测验 • 测试百分数β所属总体百分数与某一理论值或期望值p0的 差异显著性。 • 样本百分数的标准误为: n p (1 p ) 0 0 ˆ − = 故由 p p p u ˆ 0 ˆ − = 例:紫花与白花大豆杂交,在F2代共得到289株,其中紫 花208株,白花81株。如果花色受一对等位基因控制,根 据遗传学原理,F2代紫花与白花分离的比例应为3:1,即 紫花理论数为p=0.75,白花为q =1-p =0.25。问该试验是 否符合一对等位基因的的遗传规律? Test of percent hypothesis

单个样本百分数的假设测验 ·假设:Ho:p=0.75;Ha:p0.75.0=0.05, 作两尾测验uo5=1.96。 计算: 208 p= =0.7197 0.75×0.25 =0.0255 289 Op= 289 4 0.7197-0.75 =-1.19 0.0255 因为:u05=1.96,|u|(1.19)0.05。 推断:接受Ho:p=0.75,即该试验中大豆花色符合一对等位 基因的遗传规律。试验中的p=0.7197与p=0.75的差别属于随 机误差
• 假设:H0:p=0.75;HA:p≠0.75。α=0.05, 作两尾测验u.05=1.96。 0.7197 289 208 p ˆ = = 计算: 0.0255 289 0.75 0.25 ˆ = p = 1.19 0.0255 0.7197 0.75 = − − u = 因为:u.05=1.96,│u│(1.19)0.05。 推断:接受H0:p=0.75,即该试验中大豆花色符合一对等位 基因的遗传规律。试验中的p=0.7197与p=0.75的差别属于随 机误差。 单个样本百分数的假设测验
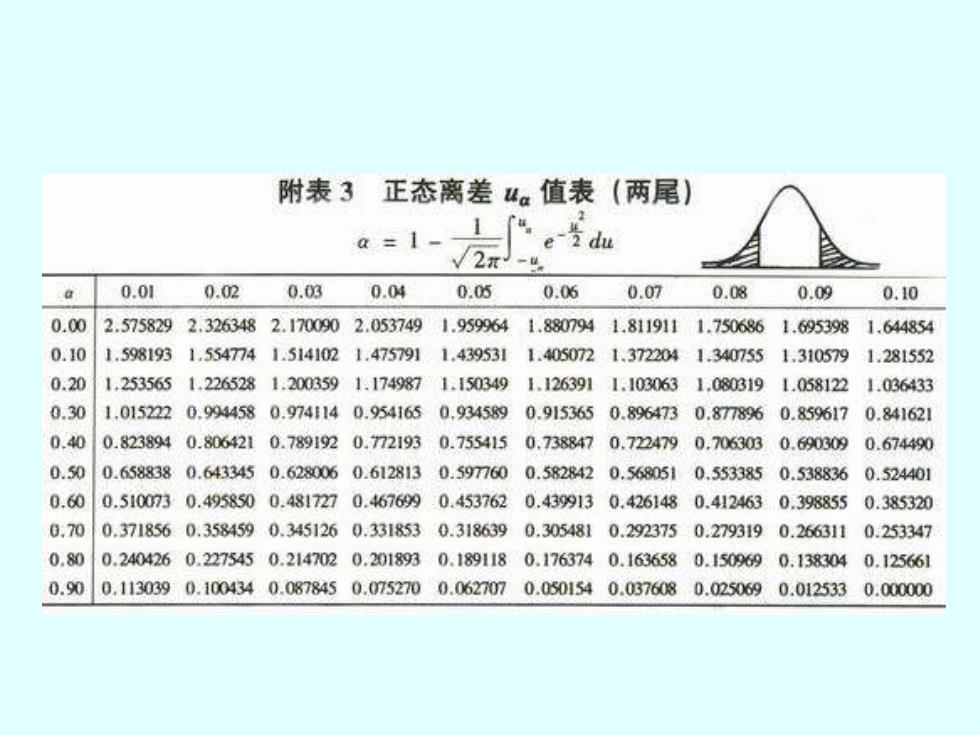
附表3正态离差4。值表(两尾) a= 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.00 2.5758292.3263482.1700902.0537491.9599641.8807941.8119111.7506861.695381.644854 0.10 1.5981931.5547741.5141021.4757911.439531 1.4050721.3722041.3407551.3105791.281552 0.20 1.2535661.2265281.2003591.1749871.1503491.1263911.1030631.0803191.058122 1.036433 0.30 1.0152220.9944580.9741140.9541650.9345890.9153650.8964730.8778960.859617 0.841621 0.40 0.8238940.8064210.7891920.7721930.7554150.7388470.722479 0.7063030.690309 0.674490 0.50 0.6588380.6433450.6280060.6128130.5977600.5828420.568051 0.5533850.538836 0.524401 0.60 0.5100730.4958500.4817270.4676990.4537620.4399130,4261480.4124630.398855 0.385320 0.70 0.3718560.3584590.3451260.3318530.3186390.3054810.2923750.2793190.266311 0.253347 0.80 0.2404260.2275450.2147020.2018930.1891180.1763740.1636580.150969 0.1383040.12566】 0.90 0.1130390.1004340.0878450.0752700.06270m0.0501540.0376080.0250690.0125330.000000

Test of percent hypothesis 2、两个样本百分数相比较的假设测验 。 测验两个样本百分数p和p,所属总体百分数p1和p2的差异 显著性。 一 般假设两个样本总体方差是相等的,即o=o 两个样本总体的个体百分数不同为p1和p2。两个样本百分 数的差数标准误为: -p2 P19+P292 n n 如果两总体的百分数相同,即p1=p2=p,91=q2=q,则:
2、两个样本百分数相比较的假设测验 • 测验两个样本百分数 和 所属总体百分数p1和p2的差异 显著性。 • 一般假设两个样本总体方差是相等的,即 • 两个样本总体的个体百分数不同为p1和p2。两个样本百分 数的差数标准误为: 2 ˆ 2 ˆp1 p2 = 1 p ˆ 2 p ˆ 2 2 2 1 1 1 ˆ ˆ 1 2 n p q n p q p − p = + 如果两总体的百分数相同,即p1=p2=p,q1=q2=q,则: − = + 1 2 ˆ ˆ 1 1 1 2 n n p p pq Test of percent hypothesis

Test of percent hypothesis 2、两个样本百分数相比较的假设测]验 在两个总体百分数p1和p2未知时,在两个总体方 差相等的前提下(σ=o员),可用两样本百分 数的加权平均值作为p1和p2的估计。即: p=龙+为 n1+n2 两个样本百分数的差数标准误为: 故有: 4=p-2 0n-p2 即可对Ho:p=p2作出假设测验
2、两个样本百分数相比较的假设测验 • 在两个总体百分数p1和p2未知时,在两个总体方 差相等的前提下( ),可用两样本百分 数的加权平均值作为p1和p2的估计。即: − = + 1 2 ˆ ˆ 1 1 1 2 n n p p pq 故有: 2 ˆ 2 ˆp1 p2 = 1 2 1 2 n n x x p + + = 两个样本百分数的差数标准误为: 1 2 ˆ ˆ 1 2 ˆ ˆ p p p p u − − = 即可对H0:p1=p2作出假设测验。 Test of percent hypothesis