
教 学目的 指数的意义以及指数编制原理 综合指数的计算方法 运用指数体系进行两因素分析
教 学 目 的 指数的意义以及指数编制原理 综合指数的计算方法 运用指数体系进行两因素分析

指数分析 第一节 指数的意义 广义理解: 一切相对数都可以称为指数。 狭义理解: 反映复杂现象总体数量变动的相对数。 复杂现象总体是相对于简单现象总体而言的。 简单现象总体指总体的单位和标志值可以直接加 以总计,如某种产品产量、产品成本等; 复杂现象总体指总体单位和标志值不能直接加以 总计,如不同产品的产量、不同商品的价格
第一节 指数的意义 指数分析 广义理解: 一切相对数都可以称为指数。 狭义理解: 反映复杂现象总体数量变动的相对数。 复杂现象总体是相对于简单现象总体而言的。 简单现象总体指总体的单位和标志值可以直接加 以总计,如某种产品产量、产品成本等; 复杂现象总体指总体单位和标志值不能直接加以 总计,如不同产品的产量、不同商品的价格
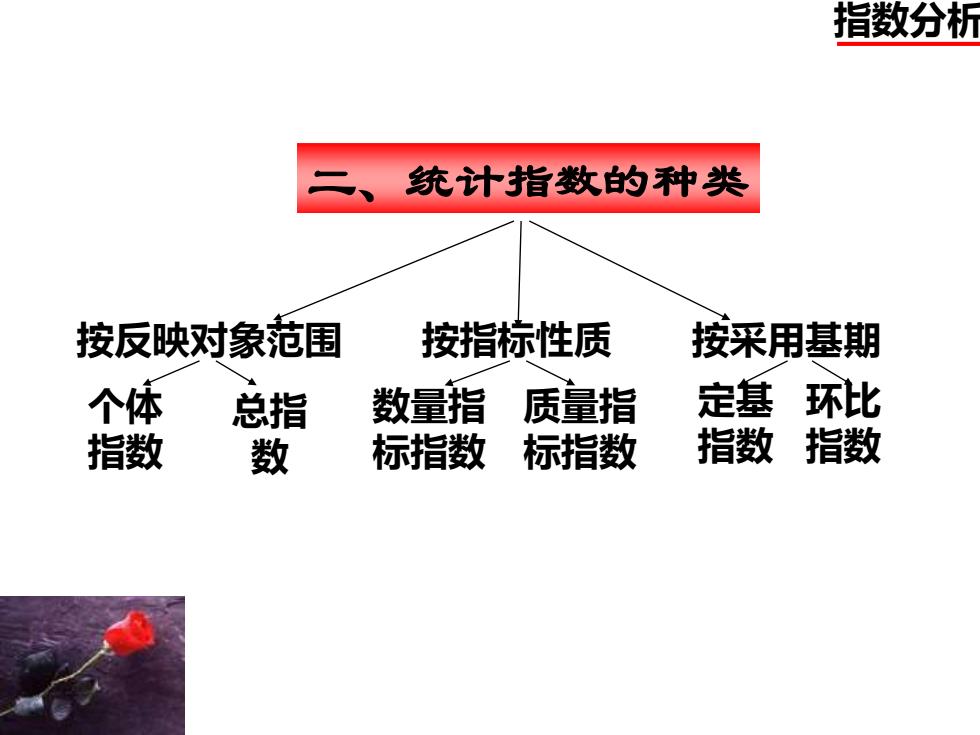
指数分析 二、统计指数的种类 按反映对象范围 按指标性质 按采用基期 个体 总 数量指 质量指 定基 环比 指数 数 标指数 标指数 指数 指数
指数分析 二、统计指数的种类 按反映对象范围 个体 指数 总指 数 按指标性质 数量指 标指数 质量指 标指数 按采用基期 定基 指数 环比 指数

指数分析 1、综合反映复杂现象总体数 量上的变动方向和程度。 2、分析现象总体 3、利用连续编制的 变动中受各个因素 三 指数数列对复杂 变动的影响方向和 程度。 统计指数 现象总体长时间 发展变化趋势进 如商品销售额的变 的作用 行分析。 动受商品销售量和 销售价格的影响程 度
指数分析 1、综合反映复杂现象总体数 量上的变动方向和程度。 三 统计指数 的作用 2、分析现象总体 变动中受各个因素 变动的影响方向和 程度。 如商品销售额的变 动受商品销售量和 销售价格的影响程 度。 3、利用连续编制的 指数数列对复杂 现象总体长时间 发展变化趋势进 行分析

指数分析 第二节纟 综合指数 是两个总量指标对比形成的指数。 (一)综合指数的编制方法 综合指数的编制方法是“先综合,后对比” 1、综合 通过解决不同度量单位的问题,来解 决综合的问题。 解决的方法: 找到与所分析的指数化指标相联系的 因素,使得指数化指标与这个因素的 乘积成为价值量指标。这个与指数化 指标相联系的因素就是同度量因素
是两个总量指标对比形成的指数。 第二节 综合指数 指数分析 (一)综合指数的编制方法 综合指数的编制方法是“先综合,后对比” 1、综合 通过解决不同度量单位的问题,来解 决综合的问题。 解决的方法: 找到与所分析的指数化指标相联系的 因素,使得指数化指标与这个因素的 乘积成为价值量指标。这个与指数化 指标相联系的因素就是同度量因素

同度量因秦的作用 例如:研究多种商品销售量和销售价格的综合变动情况 当研究销售量的变动时,销售量是数量指标,则与 之相联系的质量指标一价格,就是同度量因素 ∑(商品销售量×商品销售价格)=商品销售总额 所研究的指数化指标 同度量因素 价值量指标 当研究价格的变动时,商品价格是质量指标,则与 之相联系的数量指标销售量,就是同度量因素 ∑(商品销售量×商品销售价格)=商品销售总额 同度量因素 所研究的指数化指标 价值量指标
同度量因素的作用 当研究销售量的变动时,销售量是数量指标,则与 之相联系的质量指标——价格,就是同度量因素 当研究价格的变动时,商品价格是质量指标,则与 之相联系的数量指标——销售量,就是同度量因素 例如:研究多种商品销售量和销售价格的综合变动情况 (商品销售量 × 商品销售价格)= 商品销售总额 所研究的指数化指标 同度量因素 ∑ 价值量指标 (商品销售量 × ∑ 商品销售价格)= 商品销售总额 同度量因素 所研究的指数化指标 价值量指标

2、对比 通过解决同度量因素的时期,来解 决对比的问题。 指数分析是利用价值量指标的形式,分析其中的数量指标 或质量指标的综合变动,分析的方法就是将引进的同度量 因素的时期固定,即假定同度量因素不变,从而通过对比 反映所研究指标的变动情况。 如前例:设:销售量为q,价格为p, 下标1表示报告期,0表示基期 反映多种商品销鲁量变动的指数公式有: ∑9Po ∑4P ∑9oP ∑gp, ∑9P, 拉氏指数 帕氏指数 不变价指数
2、对比 通过解决同度量因素的时期,来解 决对比的问题。 指数分析是利用价值量指标的形式,分析其中的数量指标 或质量指标的综合变动,分析的方法就是将引进的同度量 因素的时期固定,即假定同度量因素不变,从而通过对比 反映所研究指标的变动情况。 如前例: 下标 表示报告期,表示基期 设:销售量为 ,价格为 , 1 0 q p 反映多种商品销售量变动的指数公式有: 0 0 1 0 q p q p 0 1 1 1 q p q p n n q p q p 0 1 拉氏指数 帕氏指数 不变价指数 √
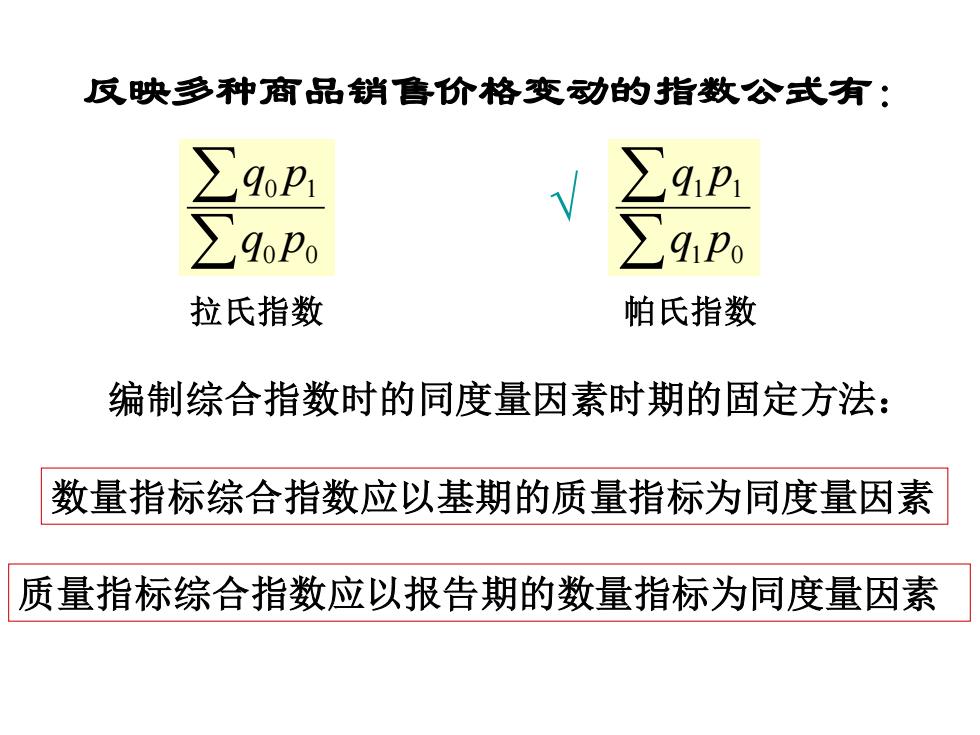
反映多种商品销价格变动的指数公式有: ∑9op1 ∑goP0 ∑9p 拉氏指数 帕氏指数 编制综合指数时的同度量因素时期的固定方法: 数量指标综合指数应以基期的质量指标为同度量因素 质量指标综合指数应以报告期的数量指标为同度量因素
反映多种商品销售价格变动的指数公式有: 0 0 0 1 q p q p 1 0 1 1 q p q p 拉氏指数 帕氏指数 √ 编制综合指数时的同度量因素时期的固定方法: 数量指标综合指数应以基期的质量指标为同度量因素 质量指标综合指数应以报告期的数量指标为同度量因素

即:当所研究的指数化指标为数量指标时,称为数 量指标综合指数,其同度量因素为基期质量指标。 数量指标综合指数: 当所研究的指数化指标为质量指标时,称为质量 指标综合指数,其同度量因素为报告期数量指标。 质量指标综合指数: 公式中:q代表数量指标,p代表质量指标 下标1代表报告期,0代表基期
数量指标综合指数: 0 0 1 0 q p q p 公式中: q代表数量指标,p代表质量指标 下标 1 代表报告期,0 代表基期 质量指标综合指数: 1 0 1 1 q p q p 当所研究的指数化指标为数量指标时,称为数 量指标综合指数,其同度量因素为基期质量指标。 当所研究的指数化指标为质量指标时,称为质量 指标综合指数,其同度量因素为报告期数量指标。 即:

(二) 综合指数分析方法 1、数量指标综合指数分析 相对数分析: 9o Po 公式分子与分母的比值反映了所研究的数 量指标报告期比基期相对综合变动程度。 绝对数分析: ∑9P。-∑qoP0 公式分子减分母的差额,反映了由于所分析的数 量指标的变动,使价值量指标增加或减少的数额
(二)综合指数分析方法 0 0 1 0 q p q p 公式分子与分母的比值反映了所研究的数 量指标报告期比基期相对综合变动程度。 q1 p0 −q0 p0 公式分子减分母的差额,反映了由于所分析的数 量指标的变动,使价值量指标增加或减少的数额。 1、数量指标综合指数分析 相对数分析: 绝对数分析: