
When are Contrarian Profits Due to Stock Market Overreaction? T● Andrew W.Lo;A.Craig MacKinlay The Review of Financial Studies,Volume 3,Issue 2 (1990).175-205. Stable URL: http://links.jstor.org/sici?sici=0893-9454%281990%293%3A2%3C175%3AWACPDT%3E2.0.CO%3B2-5 Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use,available at http://www.jstor.org/about/terms.html.JSTOR's Terms and Conditions of Use provides,in part,that unless you have obtained prior permission,you may not download an entire issue of a journal or multiple copies of articles,and you may use content in the JSTOR archive only for your personal,non-commercial use. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. The Review of Financial Studies is published by Oxford University Press.Please contact the publisher for further permissions regarding the use of this work.Publisher contact information may be obtained at http://www.jstor.org/journals/oup.html. The Review of Financial Studies 1990 Oxford University Press JSTOR and the JSTOR logo are trademarks of JSTOR,and are Registered in the U.S.Patent and Trademark Office. For more information on JSTOR contact jstor-info@umich.edu. ©2003 JSTOR http://www.jstor.org/ Tue Feb1801:39:262003

When Are Contrarian Profits Due to Stock Market Overreaction? Andrew W.Lo Sloan School of Management Massachusetts Institute of Technology A.Craig MacKinlay Wharton School University of Pennsylvania If returns on some stocks systematically lead or lag those of otbers,a portfolio strategy that sells c“vinners”and buys "losers”can produce positive expected returns,even if no stock's returns are negatively autocorrelated as virtually all models of overreaction imply.Using a particular con- trarian strategy we sbow tbat,despite negative autocorrelation in individual stock returns,weekly portfolio returns are strongly positively autocor- related and are tbe result ofimportant cross-auto- correlations.We find that the returns of large stocks lead those of smaller stocks,and we present evidence against overreaction as the only source of contrarian profits. Since the publication of Louis Bachelier's thesis The- ory ofSpeculation in 1900,the theoretical and empir- Research support from the Batterymarch Fellowship (Lo),the Geewax.Ter- ker Research Fund (MacKinlay),the National Science Foundation (Grant No.SES-8821583),the John M.Olin Fellowship at the NBER (Lo),and the Q Group is gratefully acknowledged.The authors thank Andy Abel,Michael Brennan,Werner DeBondt,Mike Gibbons,Don Keim,Bruce Lehmann,Jay Ritter,Rob Stambaugh,a referee,and seminar participants at Harvard Uni- versity,Princeton University,the University of Alberta,the University of Maryland,the University of Minnesota,the University of Western Ontario, and the Wharton School for useful suggestions and discussion.Address reprint requests to Andrew Lo,Sloan School of Management,M.I.T.,50 Memorial Drive,Cambridge,MA 02139. The Review of Financial Studies 1990 Volume 3,number 2,pp.175-205 1990 The Review of Financial Studies 0893-9454/90/$1.50

Tbe Review of Financial Studtes /v 3 n 2 1990 ical implications of the random walk hypothesis as a model for spec- ulative prices have been subjects of considerable interest to financial economists.First developed by Bachelier from rudimentary economic considerations of"fair games,"the random walk has received broader support from the many early empirical studies confirming the unpre- dictability of stock-price changes.1 Of course,as Leroy (1973)and Lucas (1978)have shown,the unforecastability of asset returns is neither a necessary nor a sufficient condition of economic equilib- rium.And,in view of the empirical evidence in Lo and MacKinlay (1988),it is also apparent that historical stock market prices do not follow random walks. This fact surprises many economists because the defining property of the random walk is the uncorrelatedness of its increments,and deviations from this hypothesis necessarily imply price changes that are forecastable to some degree.But our surprise must be tempered by the observation that forecasts of stock returns are still imperfect and may be subject to considerable forecast errors,so that "excess"' profit opportunities and market inefficiencies are not necessarily con- sequences of forecastability.Nevertheless,several recent studies maintain the possibility of significant profits and market inefficiencies, even after controlling for risk in one way or another. Some of these studies have attributed this forecastability to what has come to be known as the"stock market overreaction"'hypothesis, the notion that investors are subject to waves of optimism and pes- simism and therefore create a kind of"momentum"'that causes prices to temporarily swing away from their fundamental values [see,e.g., DeBondt and Thaler (1985,1987),DeLong,Shleifer,Summers,and Waldmann (1989),Lehmann (1988),Poterba and Summers (1988), and Shefrin and Statman(1985)].Although such a hypothesis does imply predictability,since what goes down must come up and vice versa,a well-articulated equilibrium theory of overreaction with sharp empirical implications has yet to be developed. But common to virtually all existing theories of overreaction is one very specific empirical implication:Price changes must be negatively autocorrelated for some holding period.For example,DeBondt and Thaler (1985)write:"If stock prices systematically overshoot,then their reversal should be predictable from past return data alone." Therefore,the extent to which the data are consistent with stock market overreaction,broadly defined,may be distilled into an empir- See,for example,the papers in Cootner (1964),and Fama (1965,1970).Our usage of the term "random walk"differs slightly from the classical definition of a process with independently and identically distributed increments.Since historically the property of primary economic interest has been the uncorrelatedness of increments,we also consider processes with uncorrelated but het- erogeneously distributed dependent increments to be random walks. 176

Contrarian Profits and Stock Market Overreaction ically decidable question:Are return reversals responsible for the predictability in stock returns? A more specific consequence of overreaction is the profitability of a contrarian portfolio strategy,a strategy that exploits negative serial dependence in asset returns in particular.The defining characteristic of a contrarian strategy is the purchase of securities that have per- formed poorly in the past and the sale of securities that have per- formed well.2 Selling the"winners"and buying the"losers"will earn positive expected profits in the presence of negative serial correlation because current losers are likely to become future winners and current winners are likely to become future losers.Therefore,one implication of stock market overreaction is positive expected profits from a con. trarian investment rule.It is the apparent profitability of several con- trarian strategies that has led many to conclude that stock markets do indeed overreact. In this article,we question this reverse implication,namely,that the profitability of contrarian investment strategies necessarily implies stock market overreaction.As an illustrative example,we construct a simple return-generating process in which each security's return is serially independent and yet will still yield positive expected profits for a portfolio strategy that buys losers and sells winners. This counterintuitive result is a consequence of positive cross-auto- covariances across securities,from which contrarian portfolio strat- egies benefit.If,for example,a high return for security A today implies that security B's return will probably be high tomorrow,then a con- trarian investment strategy will be profitable even if each security's returns are unforecastable using past returns of that security alone. To see how,suppose the market consists of only the two stocks,A and B;if A's return is higher than the market today,a contrarian sells it and buys B.But if A and B are positively cross-autocorrelated,a higher return for A today implies a higher return for B tomorrow on average,thus the contrarian will have profited from his long position in B on average.Nowhere is it required that the stock market over- reacts,that is,that individual returns are negatively autocorrelated. Therefore,the fact that some contrarian strategies have positive expected profits need not imply stock market overreaction.In fact, for the particular contrarian strategy we examine,over half of the expected profits are due to cross effects and not to negative autocor- relation in individual security returns. Perhaps the most striking aspect of our empirical findings is that these cross effects are generally positive in sign and have a pro- Decisions about how performance is defined and for what length of time generate as many different kinds of contrarian strategies as there are theories of overreaction. 177

The Revfew of Financial Studies /v 3 n 2 1990 nounced lead-lag structure:The returns of large-capitalization stocks almost always lead those of smaller stocks.This result,coupled with the observation that individual security returns are generally weakly negatively autocorrelated,indicates that the recently documented positive autocorrelation in weekly returns indexes is completely attributable to cross effects.This provides important guidance for theoretical models of equilibrium asset prices attempting to explain positive index autocorrelation via time-varying conditional expected returns.Such theories must be capable of generating lead-lag pat- terns,since it is the cross-autocorrelations that are the source of positive dependence in stock returns. Of course,positive index autocorrelation and lead-lag effects are also a symptom of the so-called "nonsynchronous trading"or "thin trading"problem,in which the prices of distinct securities are mis- takenly assumed to be sampled simultaneously.Perhaps the first to show that nonsynchronous sampling of prices induces autocorrelated portfolio returns was Fisher (1966);hence the nonsynchronous trad- ing problem is also known as the "Fisher effect."3 Lead-lag effects are also a natural consequence of thin trading,as the models of Cohen et al.(1986)and Lo and MacKinlay (1989)show.To resolve this issue,we examine the magnitudes of index autocorrelation and cross- autocorrelations generated by a simple but general model of thin trading.We find that,although some of the correlation observed in the data may be due to this problem,to attribute all of it to thin trading would require unrealistically thin markets. Because we focus only on the expected profits of the contrarian investment rule and not on its risk,our results have implications for stock market efficiency only insofar as they provide restrictions on economic models that might be consistent with the empirical results. In particular,we do not assert or deny the existence of "excessive" contrarian profits.Such an issue cannot be addressed without spec- ifying an economic paradigm within which asset prices are rationally determined in equilibrium.Nevertheless,we show that the contrarian investment strategy is still a convenient tool for exploring the auto- correlation properties of stock returns. In Section 1 we provide a summary of the autocorrelation properties of weekly returns,documenting the positive autocorrelation in port- folio returns and the negative autocorrelations of individual returns. Section 2 presents a formal analysis of the expected profits from a specific contrarian investment strategy under several different return- generating mechanisms and shows that positive expected profits need We refrain from this usage since the more common usage of the Fisher effect(that of Irving Fisher) is the one-for-one change in nominal interest rates with changes in expected inflation. 178

Contrarian Profits and Stock Market Overreaction not be related to overreaction.We also develop our model of non- synchronous trading and calculate the effect on the time-series prop- erties of the observed data,to be used later in our empirical analysis. In Section 3,we attempt to quantify empirically the proportion of contrarian profits that can be attributed to overreaction,and find that a substantial portion cannot be.We show that a systematic lead-lag relationship among returns of size-sorted portfolios is an important source of contrarian profits,and is the sole source of positive index autocorrelation.Using the nontrading model of Section 2,we also conclude that the lead-lag patterns cannot be completely attributed to nonsynchronous prices.In Section 4 we provide some discussion of our use of weekly returns in contrast to the much longer-horizon returns used in previous studies of stock market overreaction,and we conclude in Section 5. 1.A Summary of Recent Findings In Table 1 we report the first four autocorrelations of weekly equal- weighted and value-weighted returns indexes for the sample period from July 6,1962,to December 31,1987,where the indexes are constructed from the Center for Research in Security Prices (CRSP) daily returns files.During this period,the equal-weighted index has a first-order autocorrelation p,of approximately 30 percent.Since its heteroskedasticity-consistent standard error is .046,this autocorre- lation is statistically different from zero at all conventional signifi- cance levels.The subperiod autocorrelations show that this signifi- cance is not an artifact of any particularly influential subsample; equal-weighted returns are strongly positively autocorrelated throughout the sample.Higher-order autocorrelations are also pos- itive although generally smaller in magnitude,and decay at a some what slower rate than the geometric rate of an autoregressive process of order 1 [AR(1)](for example,p is 8.8 percent whereas p2 is 11.6 percent). To develop a sense of the economic importance of the autocorre- lations,observe that the R2 of a regression of returns on a constant and its first lag is the square of the slope coefficient,which is simply the first-order autocorrelation.Therefore,an autocorrelation of 30 percent implies that 9 percent of weekly return variation is predictable using only the preceding week's returns.In fact,the autocorrelation coefficients implicit in Lo and MacKinlay's (1988)variance ratios are as high as 49 percent for a subsample of the portfolio of stocks in the smallest-size quintile,implying an R2 of about 25 percent. Unless stated otherwise,we take returns to be simple returns and not continuously compounded. 179
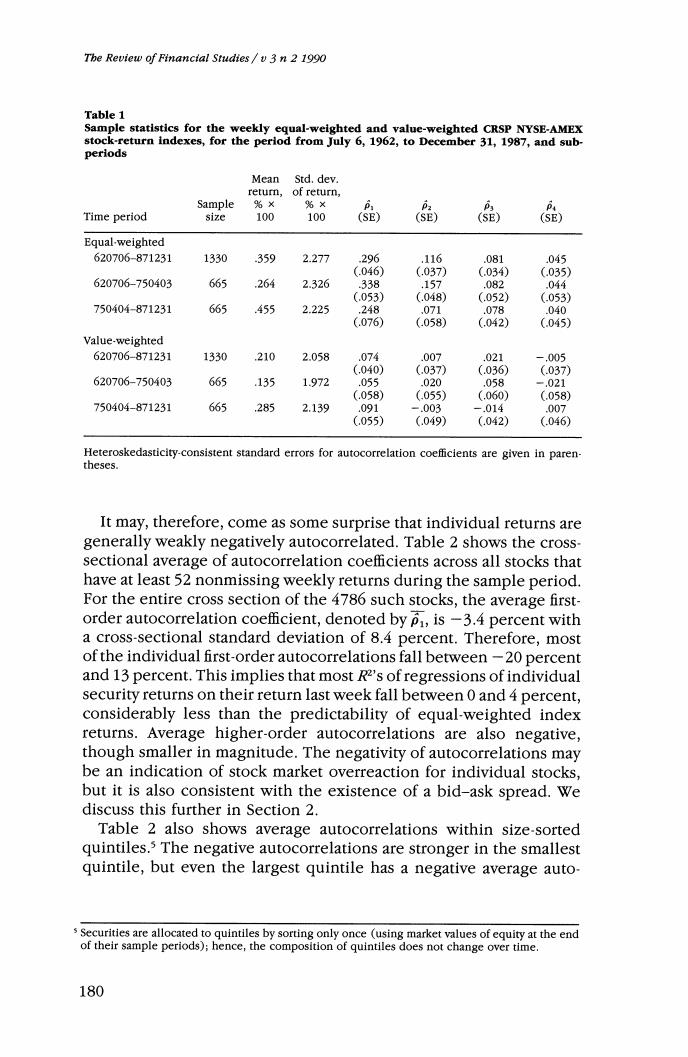
The Review of Financial Studies /v 3 n 2 1990 Table 1 Sample statistics for the weekly equal-weighted and value-weighted CRSP NYSE-AMEX stock-return indexes,for the period from July 6,1962,to December 31,1987,and sub- periods Mean Std.dev. return, of return, Sample %× %× P Time period size 100 100 (SE) (SE) (SE) (SE) Equal-weighted 620706-871231 1330 359 2.277 296 .116 .081 .045 (.046) (.037) (.034) (.035) 620706-750403 665 264 2.326 338 .157 .082 .044 (.053) (.048) (.052) (.053) 750404-871231 665 .455 2.225 ,248 .071 .078 .040 (.076) (.058) (.042) (.045) Value-weighted 620706-871231 1330 ,210 2.058 .074 .007 .021 -.005 (.040) (.037) (.036) (.037) 620706-750403 665 .135 1.972 .055 .020 .058 -.021 (.058) (.055) (.060) (.058) 750404-871231 665 ,285 2.139 .091 -.003 -.014 .007 (.055) (.049) (.042) (.046) Heteroskedasticity-consistent standard errors for autocorrelation coefficlents are given in paren- theses. It may,therefore,come as some surprise that individual returns are generally weakly negatively autocorrelated.Table 2 shows the cross- sectional average of autocorrelation coefficients across all stocks that have at least 52 nonmissing weekly returns during the sample period. For the entire cross section of the 4786 such stocks,the average first- order autocorrelation coefficient,denoted by p,is-3.4 percent with a cross-sectional standard deviation of 8.4 percent.Therefore,most of the individual first-order autocorrelations fall between-20 percent and 13 percent.This implies that most R2's of regressions of individual security returns on their return last week fall between 0 and 4 percent, considerably less than the predictability of equal-weighted index returns.Average higher-order autocorrelations are also negative, though smaller in magnitude.The negativity of autocorrelations may be an indication of stock market overreaction for individual stocks, but it is also consistent with the existence of a bid-ask spread.We discuss this further in Section 2. Table 2 also shows average autocorrelations within size-sorted quintiles.s The negative autocorrelations are stronger in the smallest quintile,but even the largest quintile has a negative average auto- s Securities are allocated to quintiles by sorting only once (using market values of equity at the end of their sample periods);hence,the composition of quintiles does not change over time. 180
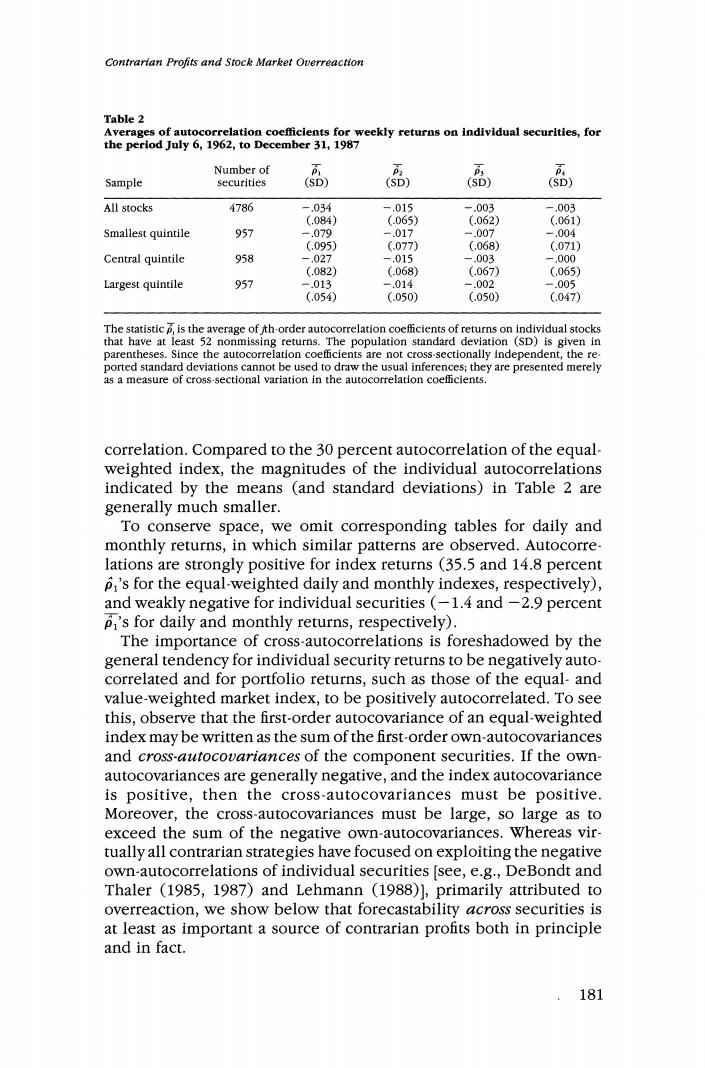
Contrarian Profits and Stock Market Overreaction Table 2 Averages of autocorrelation coefficients for weekly returns on individual securities,for the period July 6,1962,to December 31,1987 Number of Sample securities (SD) (SD) 高 All stocks 4786 -.034 -,015 -.003 -.003 (.084) (.065) (.062) (.061) Smallest quintile 957 -.079 -.017 -.007 -.004 (.095) (.077) (.068) (.071) Central quintile 958 -,027 -.015 -.003 -,000 (.082) (.068) (.067) (,065) Largest quintile 957 -.013 -.014 -.002 -.005 (.054) (.050) (.050) (.047) The statistic p,is the average of th-order autocorrelation coefficients of returns on individual stocks that have at least 52 nonmissing returns.The population standard deviation (SD)is given in parentheses.Since the autocorrelation coefficients are not cross-sectionally independent,the re- ported standard deviations cannot be used to draw the usual inferences;they are presented merely as a measure of cross-sectional variation in the autocorrelation coefficients. correlation.Compared to the 30 percent autocorrelation of the equal- weighted index,the magnitudes of the individual autocorrelations indicated by the means (and standard deviations)in Table 2 are generally much smaller. To conserve space,we omit corresponding tables for daily and monthly returns,in which similar patterns are observed.Autocorre lations are strongly positive for index returns (35.5 and 14.8 percent p,'s for the equal-weighted daily and monthly indexes,respectively), and weakly negative for individual securities (-1.4 and-2.9 percent pI's for daily and monthly returns,respectively). The importance of cross-autocorrelations is foreshadowed by the general tendency for individual security returns to be negatively auto- correlated and for portfolio returns,such as those of the equal-and value-weighted market index,to be positively autocorrelated.To see this,observe that the first-order autocovariance of an equal-weighted index may be written as the sum of the first-order own-autocovariances and cross-autocovariances of the component securities.If the own- autocovariances are generally negative,and the index autocovariance is positive,then the cross-autocovariances must be positive. Moreover,the cross-autocovariances must be large,so large as to exceed the sum of the negative own-autocovariances.Whereas vir- tually all contrarian strategies have focused on exploiting the negative own-autocorrelations of individual securities [see,e.g.,DeBondt and Thaler (1985,1987)and Lehmann (1988)],primarily attributed to overreaction,we show below that forecastability across securities is at least as important a source of contrarian profits both in principle and in fact. .181

The Review of Financial Studies /v 3 n 2 1990 2.Analysis of Contrarian Profitability To show the relationship between contrarian profits and the cross effects that are apparent in the data,we examine the expected profits of one such strategy under various return-generating processes.Con- sider a collection of Nsecurities and denote by R,the N x 1 vector of their period t returns[R,···RwJ'.For convenience,we maintain the following assumption throughout this section: Assumption 1.R,is a jointly covariance-stationary stocbastic process with expectation ER,]=u=u,u2···4w'and autocovariance matrices E[(R-)(R-u)]=T wbere,with no loss ofgenerality, we take k=0 since =I.6 In the spirit of virtually all contrarian investment strategies,consider buying stocks at time t that were losers at time t-k and selling stocks at time t that were winners at time t-k,where winning and losing is determined with respect to the equal-weighted return on the market.More formally,if (k)denotes the fraction of the port- folio devoted to security i at time t,let w(k)=-(1/N0(Rm-k-Rnt-)i=1,..,N (1) where Rm=R/N is the equal-weighted market index.7 If, for example,k=1,then the portfolio strategy in period t is to short the winners and buy the losers of the previous period,t-1.By construction,w,(k)=[o(k)w2()···ωw()]'is an arbitrage port- folio since the weights sum to zero.Therefore,the total investment long (or short)at time t is given by I,(k)where lo(1 (2) Since the portfolio weights are proportional to the differences between the market index and the returns,securities that deviate more posi- tively from the market at time t-k will have greater negative weight 6Assumption 1 is made for notational simplicity,since joint covariance-stationarity allows us to eliminate time indexes from population moments such as and I;the qualitative features of our results will not change under the weaker assumptions of weakly dependent heterogeneously distributed vectors R.This would merely require replacing expectations with corresponding prob- ability limits of suitably defined time averages.The empirical results of Section 3 are based on these weaker assumptions;interested readers may refer to Assumptions A1-A3 in Appendix B. This is perhaps the simplest portfolio strategy that captures the essence of the contrarian principle. Lehmann (1988)also considers this strategy,although he employs a more complicated strategy in his empirical analysis in which the portfolio weights [Equation (1)]are renormalized each period by a random factor of proportionality,so that the investment is always $1 long and short.This portfolio strategy is also similar to that of DeBondt and Thaler (1985,1987),although in contrast to our use of weekly returns,they consider holding periods of three years.See Section 4 for further discussion. 182

Contrartan Profits and Stock Market Overreaction in the time t portfolio,and vice versa.Such a strategy is designed to take advantage of stock market overreactions as characterized,for example,by DeBondt and Thaler (1985):"(1)Extreme movements in stock prices will be followed by extreme movements in the oppo- site direction.(2)The more extreme the initial price movement,the greater will be the subsequent adjustment."The profit (k)from such a strategy is simply x,()=∑@()R。 (3) Rearranging Equation (3)and taking expectations yields the follow- ing: 肉1-g-点如)一片这a- (4) where um=E[Rm]=u'/N and tr()denotes the trace operator.8 The first term of Equation (4)is simply the kth-order autocovariance of the equal-weighted market index.The second term is the cross-sec- tional average of the kth-order autocovariances of the individual secu- rities,and the third term is the cross-sectional variance of the mean returns.Since this last term is independent of the autocovariances Ie and does not vary with k,we define the profitability indexL=L(T) and the constant o2(u)as (5) Thus, E[T,()]=L。-σ2(4) (6) For purposes that will become evident below,we rewrite L as Lw=C6十O (7) where G=1 KT4-tr(T] (8) Hence, π(k]=C+O。-σ2(u) (9) The derivation of Equation(4)is included in Appendix 1 for completeness.This is the population counterpart of Lehmann's (1988)sample moment equation (5)divided by N. 183