
Stock Prices and Volume STOR A.Ronald Gallant;Peter E.Rossi;George Tauchen The Review of Financial Studies,Volume 5,Issue 2 (1992).199-242 Stable URL: hutp://links.jstor.org/sici?sici=0893-9454%281992%295%3A2%3C199%3ASPAV3E2.0.CO%3B2-Y Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use,available at http://www.jstor.org/about/terms.html.JSTOR's Terms and Conditions of Use provides,in part,that unless you have obtained prior permission,you may not download an entire issue of a journal or multiple copies of articles,and you may use content in the JSTOR archive only for your personal,non-commercial use. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. The Review of Financial Studies is published by Oxford University Press.Please contact the publisher for further permissions regarding the use of this work.Publisher contact information may be obtained at http://www.jstor.org/journals/oup.html. The Review of Financial Studies 1992 Oxford University Press JSTOR and the JSTOR logo are trademarks of JSTOR,and are Registered in the U.S.Patent and Trademark Office. For more information on JSTOR contact jstor-info@umich.edu. ©2003 JSTOR http://www.jstor.org/ Mon Feb1708:55:332003

Stock Prices and Volume A.Ronald Gallant North Carolina State University Peter E.Rossi University of Chicago George Tauchen Duke University We undertake a comprebensive investigation of price and volume co-movement using daily New York Stock Excbange data from 1928 to 1987.We adjust tbe data to take into account well-known calendar effects and long-run trends.To describe the process,we use a seminonparametric estimate of the joint density of current price change and volume conditional on past price changes and vol- ume.Four empirical regularities are found:(i) positive correlation between conditional volatility and volume;(ii)large price movements are fol- lowed by bigb volume;(iii)conditioning on lagged volume substantially attenuates the 'leverage" effect;and (iv)after conditioning on lagged vol- ume,tbere is a positive risk-return relation. The recent history of the stock market has been char- acterized by sharp downward price movements accompanied by high volume and associated with increased future volatility.On Black Monday II (October 19,1987),the s&P 500 composite index plunged 22.9 percent on the second highest volume This article is based upon work supported by the National Science Foun dation under grants SES-8808015 and SES-8810357,North Carolina Agricul- tural Experiment Station Project NCO-6134,and the Graduate School of Business of the University of Chicago.We are grateful to David Hendry, David Hsieh,William Schwert,Robert Stambaugh,and Tim Bollerslev (the referee)for many helpful comments.Address requests for reprints to George Tauchen,Department of Economics,Duke University,Durham,NC 27706. The Review of Financial Studies 1992 Volume 5,number 2,pp.199-242 1992 The Review of Financial Studies 0893-9454/92/$1.50

The Review of Financial Studies /v 5 n 2 1992 ever recorded (604 million shares).On the day after the crash of 1987,the S&P 500 index rose by 5.2 percent on the highest volume ever recorded of 608 million shares.Two days after the crash on October 21,the S&P 500 index rose 8.7 percent (the seventh highest one-day increase in the period from 1928 to 1989)with the trading of 450 million shares.In 1989,the 7 percent drop on October 13 was accompanied by a 50 percent increase in volume and followed by heavy trading on Monday,October 16,of two and a half times the normal volume.These events of the late 1980s suggest strong inter- relationships among the sign and magnitude of price movements,the volatility of prices,and the trading volume. Studies of volatility dynamics examine the relationship between large price movements and increased volatility.For the (univariate) S&P composite price index data,French,Schwert,and Stambaugh (1987)employ the GARCH specification developed by Bollerslev (1986,1987).Engle and Bollerslev (1986)extend the GARCH model to include a unit root in the variance evolution term to accommodate the observed strong persistence in conditional variances.Nelson (1989, 1991)introduces an "exponential"GARCH model that overcomes some problems with positivity restrictions and symmetry in the con- ditional variance function associated with standard GARCH models. Efforts to explore the determination of the risk premium for stocks have employed a variety of ARCH-M specifications [see French, Schwert,and Stambaugh (1987),Bollerslev,Engle,and Wooldridge (1988),and Nelson(1989,1991)].Pagan and Hong (1991)and Harvey (1991)use nonparametric techniques to study the risk premium.The presence of ARCH-like variance shifts is thus well-documented,though there is considerable disagreement about which variant of a para- metric ARCH model is most appropriate to describe the price change process. In this study,we investigate the joint dynamics of price changes and volume on the stock market.We use daily data on the S&P com- posite index and total NYSE trading volume from 1928 to 1987,which is a bivariate time series of 16,127 observations. We use nonparametric methods throughout.The main reason for choosing nonparametric methods is that we wish to avoid bias due to a specification error.With parametric methods,there is always a risk that specification error will seriously bias an estimate and thereby lead to a spurious result.The best-known discussion of this point in the econometrics literature is White (1980).An excellent illustration of an instance where the use of nonparametric methods uncovered a specification error that was responsible for an incorrect sign on an important variable is Engle et al.(1986).With respect to financial market data,Gallant,Hsieh,and Tauchen (1991)find that side lobes 200

Stock Prices and Volume in the error density (which are ruled out in customary,parametric, ARCH specifications)are clearly revealed in a nonparametric analysis and are the apparent source of spurious findings of nonlinearity over and above ARCH.Engle and Gonzales-Rivera (1991)analyze these same data using an alternative nonparametric technique.They confirm these departures from customary parametric specifications and per- form Monte Carlo simulations to assess the consequences for para- metric analysis. Previous empirical work on the price and volume relationship has focused primarily on the contemporaneous relationship between price changes and volume.Transactions level,hourly,daily,weekly,and monthly data on individual stocks,futures,and stock price indices have been used to document a positive correlation between the abso- lute value of stock price changes and volume [see Karpoff(1987)and Tauchen and Pitts (1983)for summaries of this literature].Foster and Viswanathan (1990)use transactions level data to examine within- day price-volume relations;Mulherin and Gerety (1988)use both hourly and daily volume and returns data to document the relation- ship between the magnitude of price changes and volume,as well as patterns in volume by time of day and week for the period from 1900 to 1987.Lamoureux and Lastrapes (1991)enter volume directly into the GARCH variance equation in their analysis of individual stock returns data.Schwert (1989)uses monthly aggregates of daily data and finds a positive relationship between estimated volatility and current and lagged volume growth rates in linear distributed lag and VAR models.With the exception of Mulherin and Gerety (1988),most empirical studies using daily or within-day data examine relatively short time periods of between 3 and 5 years. Generally speaking,the empirical work on price-volume relations tends to be very data-based and not guided by rigorous,equilibrium models of market behavior.The models are more statistical than economic in character,and typically neither the optimization prob- lem facing agents nor the information structure is fully specified.The intrinsic difficulties of specifying plausible,rigorous,and imple- mentable models of volume and prices are the reasons for the informal modeling approaches commonly used. Recently,some interesting theoretical work investigated factors such as heterogeneous agents and incomplete markets,which are substantial complications of the familiar representative agent asset- pricing models.For example,Admati and Pfleiderer (1988,1989) explore the implications for within-day and weekend volume and price movements of a model comprised of informed traders and liquidity traders.Huffman (1987)presents a capital growth model with overlapping generations that yields a contemporaneous volume- 201

Tbe Review of Financial Studies /v 5 n 2 1992 price relationship.More recently,Huffman (1988)and Ketterer and Marcet (1989)examine trading volume and welfare issues in various economies comprised of heterogeneous infinitely lived agents facing limited trading opportunities [also,see Andersen (1991)].Existing models,however,do not confront the data in its full complexity and have not evolved sufficiently to guide the specification of an empirical model of daily stock market data.For instance,there seems to be no model with dynamically optimizing,heterogeneous agents that can jointly account for major stylized facts-serially correlated volatility, contemporaneous volume-volatility correlation,and excess kurtosis of price changes-each of which we discuss below. In this article,we undertake an empirical investigation of the dynamic interrelationships among price and volume movements on the stock market.Our work is motivated in part by the recent events on the stock market,which suggest that more can be learned about the market-and,in particular,about volatility-by studying prices in conjunction with volume,instead of prices alone.It is also moti- vated by an objective of providing a full set of stylized facts that theoretical work will ultimately have to confront.Because of the limitations of existing theory,the empirical work is not organized around the specification and testing of a particular model or class of models.Instead,the empirical effort is mainly data-based.We begin with an informal graphical look at the data and then proceed ulti- mately to the estimation and interpretation of a seminonparametric (SNP)model of the conditional joint density of market price changes and volume in Section 3. The investigation has four objectives:(i)to analyze the relation- ships between contemporaneous volume and volatility in an esti- mation context that explicitly accounts for conditional heteroskedas- ticity and other forms of conditional heterogeneity;(ii)to characterize the intertemporal relationships among prices,volatility,and volume; (iii)to examine the "leverage"effect,which is an asymmetry about the vertical axis in a plot of the conditional variance of current price change against past price change,and to examine the extent to which conditioning on past volume reduces or increases the asymmetry;and (iv)to determine what,if any,relationship there is between the conditional mean and variances of price changes. These objectives relate to features of the conditional density of the price change and volume data,and not to the signs and magnitudes of specific parameters.The conditional density is the fundamental statistical object of interest,as it embodies all of the information about the probabilistic structure of the data.Hence,as noted above,we employ a seminonparametric approach to estimate the density directly. 202

Stock Prices and Volume We also use kernel-based methods and subperiod analysis to corrob- orate major findings. The remainder of the article is organized as follows.In Section 1, we describe the data sources and the adjustments made to remove systematic calendar and trend effects from the location and scale of the price change and volume series.In Section 2,we review the seminonparametric approach to modeling nonlinear time series and undertake the estimation,which involves a specification search and diagnostic checking procedures.In Section 3,we examine various features of the fitted SNP density in order to address the basic research goals described above.In Section 4,we summarize our findings. 1.Data Sources and Adjustments The raw data consist of the daily closing value of the S&P composite stock index and the daily volume of shares traded on the NYSE.Price index data for the period from 1928 to 1985 were generously supplied to us by Robert Stambaugh.We extended the price data through 1987. The volume data is from the Standard Poor's Security Price Index Record(various years).The Security Price Record appears to be the only source of a long-time series on daily market volume. The S&P composite price index is a value-weighted,arithmetic index of prices of common stocks,most of which are traded on the NYSE.In the period before March 1,1957,the S&P composite index was made up of 90 stocks.On March 1,1957,the index was broadened to include 500 stocks.In July 1976,Standard Poor added a group of financial stocks to the s&P 500 composite index.Some of these financial stocks are traded over-the-counter,so that in recent years the S&P 500 has included a few non-NYSE stocks. The raw price index series,P,is differenced in the logs to create the raw price change series,100(log P:-log P,-1),and is plotted in the top panel of Figure 1.There is a U-shaped pattern in the volatility of the raw price change series:in the early 1930s and the late 1980s, the volatility is very high,while in the middle part of the sample the volatility is low.We do not expect to explain or model long-run shifts in the volatility of price movements.We decided,therefore,to allow for a quadratic trend in the variance of the raw price change series in order to focus our modeling efforts on the short-run pattern of conditional heteroskedasticity. Many authors have noted systematic calendar effects in both the mean and variance of price movements.Rozeff and Kinney (1976) report a January seasonal in stock market index returns (i.e.,mean returns are higher in January).Keim (1983)refined this analysis of the January seasonal by studying the magnitude of the seasonal for 203
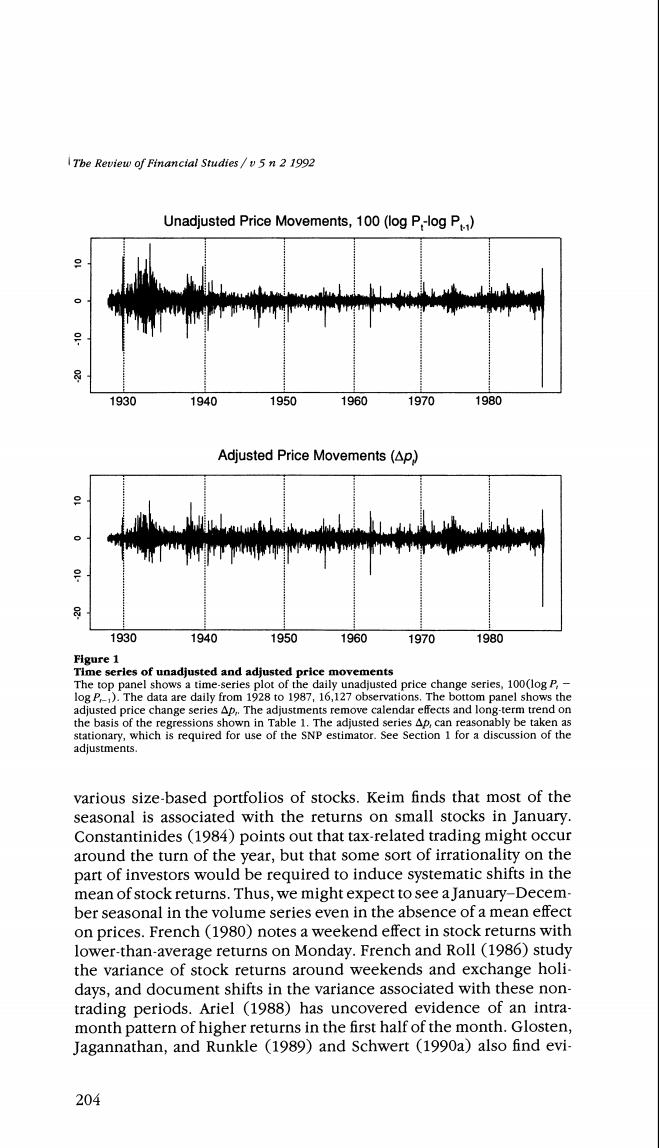
The Review of Financial Studies /v 5 n 2 1992 Unadjusted Price Movements,100(log P-log P) 1930 1940 1950 1960 1970 1980 Adjusted Price Movements(Ap) 1930 1940 1950 1960 1970 1980 Figure 1 Time serles of unadjusted and adjusted price movements The top panel shows a time-series plot of the daily unadjusted price change series,100(log P,- log P).The data are daily from 1928 to 1987,16,127 observations.The bottom panel shows the adjusted price change series Ap,.The adjustments remove calendar effects and long-term trend on the basis of the regressions shown in Table 1.The adjusted series Ap,can reasonably be taken as stationary,which is required for use of the SNP estimator.See Section 1 for a discussion of the adjustments. various size-based portfolios of stocks.Keim finds that most of the seasonal is associated with the returns on small stocks in January. Constantinides (1984)points out that tax-related trading might occur around the turn of the year,but that some sort of irrationality on the part of investors would be required to induce systematic shifts in the mean of stock returns.Thus,we might expect to see a January-Decem- ber seasonal in the volume series even in the absence of a mean effect on prices.French (1980)notes a weekend effect in stock returns with lower-than-average returns on Monday.French and Roll (1986)study the variance of stock returns around weekends and exchange holi- days,and document shifts in the variance associated with these non- trading periods.Ariel (1988)has uncovered evidence of an intra- month pattern of higher returns in the first half of the month.Glosten, Jagannathan,and Runkle (1989)and Schwert (1990a)also find evi- 204

Stock Prices and Volume dence of monthly and daily seasonals in means and standard devia- tions of returns. In order to adjust for these documented shifts in both the mean and variance of the price and volume series,we perform a two-stage adjustment process in which systematic effects are first removed from the mean and then from the variance.We use the following set of dummy and time-trend variables in the adjustment regressions to capture these systematic effects: 1.Day-of-the-week dummies (one for each day,Tuesday through Saturday). 2.Dummy variables for each number of nontrading days preceding the current trading day (dummies for each of 1,2,3,and 4 nontrading days since the preceding trading day).These"gap"variables capture the effects of holidays and weekends.The distribution of these gaps in the trading record are as follows: gap of one nontrading day:1339 gap of two nontrading days:1873 gap of three nontrading days:223 gap of four nontrading days:5 3.Dummy variables for months of March,April,May,June,July, August,September,October,and November. 4.Dummy variables for each week of December and January.These variables are designed to accommodate the well-known "January' effect in both the mean and variance of prices and volume. 5.Dummy variables for each year,1941 to 1945. 6.t,t2,time trend variables.(Note:these variables are not included in the mean regressions for the price change.) This list of variables is generally self-explanatory,though we should elaborate on a few points concerning the "gap"variables in the sec- ond group.As to frequency,there are more one-day gaps and fewer two-day gaps than one might expect as a result of trading on Saturdays for the years 1928 through mid-year 1949.As to encoding,if trading occurred on the preceding day,then there is no gap in the trading record and no dummy is included;there are 12,686 such days.The Bank Holiday of 1933 is associated with a gap of 11 days over which the increase in the raw S&P index is the largest close-to-close move- ment in the entire data set.No dummy is included for this single 11- day gap because doing so would,in effect,replace the largest upward change in the price index with the unconditional mean of the price changes,which in our view would not accurately reflect what tran- spired over the Bank Holiday.Finally,in both the adjustments for the mean and variance of volume,the coefficients of the four gap variables 205

Tbe Review of Financial Studies /v 5 n 2 1992 are constrained to lie along a line.Without such constraints,the adjustment process itself appears to create some very extreme and implausible values in the adjusted volume process,particularly for the five days in which gap =4. To perform the adjustment,we first regress 100(log P:-log P1) or log(V)(V,represents volume)on the set of adjustment variables: w=xB+u (mean equation). Here w is the series to be adjusted and x contains the adjustment regressors.The least squares residuals are taken from the mean equa- tion to construct a variance equation: log(42)=x'y +e (variance equation). This regression is used to standardize the residuals from the mean equation,and then a final linear transformation is performed to cal- culate adjusted w: wadi a+b(i/exp(x'y/2)), where a and b are chosen so that the sample means and variances of w and wadi are the same.The linear transformation makes the units of measurement of adjusted and unadjusted data the same,which facilitates interpretation of our empirical results.In what follows,Ap. denotes adjusted 100(log P,-log P-1)and v,denotes adjusted log V.. Table 1 shows the estimated coefficients in the mean and variance adjustment equations for the price change series.The patterns confirm the well-known day-of-the-week and January effects:Monday has a lower return than any other day of the week,which is seen by noting that the coefficients of all other day-of-the-week dummies are positive. Price changes are higher in the last week of December and the first week of January.The effect of wartime seems to be confined to a reduction in the variance. The Ap,series is plotted in the bottom panel of Figure 1.The adjustments make the series appear more homogeneous,thereby allowing us to focus on the day-to-day dynamic structure under an assumption of stationarity. We do not regard the Ap,series as a market-returns series since the S&P index is not adjusted for dividend payout.If dividend payout is lumpy and the payout has an appreciable effect on the index (because of groups of stocks going ex-dividend together),then the lumpy dividends can create yet another possible systematic calendar effect. In order to investigate the lumpiness of dividend payout,we obtained daily data on the total dividend payout of the s&P 100 index in the period 1979 to 1987.[These data are used in Harvey and Whaley (1991),and we thank the authors for allowing us access to these data.] 206
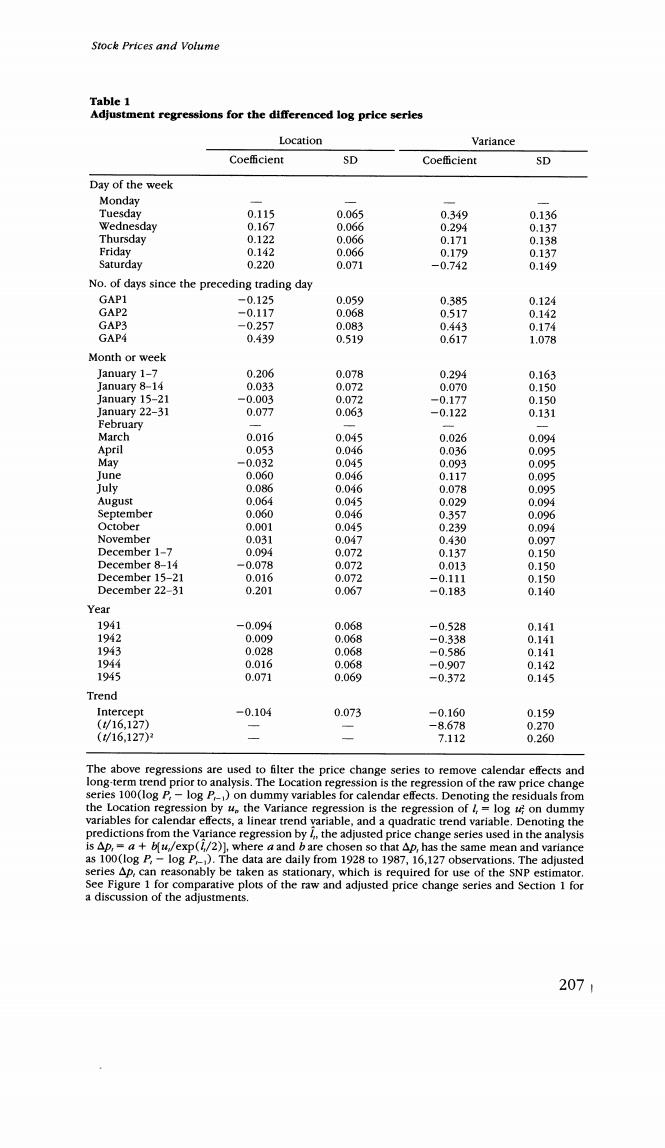
Stock Prices and Volume Table 1 Adjustment regressions for the differenced log price serles Location Variance Coefficient SD Coe伍cient SD Day of the week Monday Tuesday 0.115 0.065 0.349 0.136 Wednesday 0.167 0.066 0.294 0.137 Thursday 0.122 0.066 0.171 0.138 Friday 0.142 0.066 0.179 0.137 Saturday 0.220 0.071 -0.742 0.149 No.of days since the preceding trading day GAP1 -0.125 0.059 0.385 0.124 GAP2 -0.117 0.068 0.517 0.142 GAP3 -0.257 0.083 0.443 0.174 GAP4 0.439 0.519 0.617 1.078 Month or week January 1-7 0.206 0.078 0.294 0.163 January 8-14 0.033 0.072 0.070 0.150 January 15-21 -0.003 0.072 -0.177 0.150 January 22-31 0.077 0.063 -0.122 0.131 February March 0.016 0.045 0.026 0.094 April 0.053 0.046 0.036 0.095 May -0.032 0.045 0.093 0.095 lune 0.060 0.046 0.117 0.095 July 0.086 0.046 0.078 0095 August 0.064 0.045 0.029 0.094 September 0.060 0.046 0.357 0.096 October 0.001 0.045 0.239 0.094 November 0.031 0.047 0.430 0.097 December 1-7 0.094 0.072 0.137 0.150 December 8-14 -0.078 0.072 0.013 0.150 December 15-21 0.016 0.072 -0.111 0.150 December 22-31 0.201 0.067 -0.183 0.140 Year 1941 -0.094 0.068 -0.528 0.141 1942 0.009 0.068 -0.338 0.141 1943 0.028 0.068 -0.586 0.141 1944 0.016 0.068 =0.907 0.142 1945 0.071 0.069 -0.372 0.145 Trend Intercept -0.104 0.073 -0.160 0.159 (/16,127) -8.678 0.270 (16.127) 7.112 0.260 The above regressions are used to filter the price change series to remove calendar effects and long-term trend prior to analysis.The Location regression is the regression of the raw price change series 100(log P,-log P-)on dummy variables for calendar effects.Denoting the residuals from the Location regression by ue the variance regression is the regression of /,log u;on dummy variables for calendar effects,a linear trend variable,and a quadratic trend variable.Denoting the predictions from the Variance regression by the adjusted price change series used in the analysis is Ap,=a+bfu/exp(/2)],where a and b are chosen so that Ap,has the same mean and variance as 100(log P,-log P).The data are daily from 1928 to 1987,16,127 observations.The adjusted series Ap,can reasonably be taken as stationary,which is required for use of the SNP estimator See Figure 1 for comparative plots of the raw and adjusted price change series and Section 1 for a discussion of the adjustments. 207