
Review of Economic Studies (1991)58,529-546 0034-6527/91/00320529$02.00 C1991 The Review of Economic Studies Limited Speculative Dynamics DAVID M.CUTLER MIT JAMES M.POTERBA MIT and NBER and LAWRENCE H.SUMMERS Harvard University and NBER First version received January 1990;final version accepted February 1991 (Eds.) This paper presents evidence on the characteristic speculative dynamics of returns on stocks, bonds,foreign exchange,real estate,collectibles,and precious metals.It highlights four stylized facts.First,returns tend to be positively serially correlated at high frequency.Second,they are weakly negatively serially correlated over long horizons.Third,deviations of asset values from proxies for fundamental value have predictive power for returns.Fourth,short term interest rates are negatively correlated with excess returns on other assets.The similarity of the results across markets suggests that they may be due to inherent features of the speculative process Many recent studies have rejected the hypothesis of constant ex ante returns in a variety of different speculative markets.There is evidence that stock returns for the United States are weakly serially correlated,that dividend yields have predictive power for returns,that the slope of the yield curve predicts long-term bond returns,that interest rate spreads predict excess returns in the foreign exchange market,and more controversially,that asset markets display excess volatility.Research attempting to explain these findings has either challenged the statistical basis of rejections of the constant required return model, or sought to explain varying risk premia with changing risk factors. An alternative view is that variations in ex ante returns and asset market volatility arise primarily from what we have elsewhere labelled"speculative dynamics"-interac- tions between different types of traders,some of whom are not rational in the conventional sense of trading on the basis of all publicly available information.Distinguishing conclus- ively between the speculative dynamics view and the conventional view of asset market fluctuations is inherently very difficult,given the limited amount of data on asset returns and the difficulty of satisfactorily proxying for risk factors. This paper extends our research on speculative dynamics by introducing a larger and more diverse data set on speculative returns than has previously been analyzed. These data suggest four regularities in asset returns.First,asset returns are positively serially correlated at high frequencies.Second,returns are negatively serially correlated at lower frequencies.Third,there is a tendency toward"fundamental reversion"in asset prices.Finally,when short-term interest rates are high,the excess returns on other assets are low.Not all of these patterns emerge in all markets,but each appears in many different markets.Since risk factors might be expected to operate quite differently in different markets,we tentatively interpret the common patterns as evidence in favour of theories emphasizing speculative dynamics. 529 Copyright O 2001 All Rights Reserved

530 REVIEW OF ECONOMIC STUDIES This paper is organized as follows.Section one describes the data set covering asset returns in various markets.The second section reports the autocorrelogram of the various returns,emphasizing the similarities across markets.Section three discusses issues relating to fundamental reversion as well as the predictive power of short-term interest rates.The final section concludes by comparing the plausibility of the speculative dynamics and the time-varying returns interpretations of our results,and identifying directions for further research. 1.ASSET-RETURNS DATA This section describes the data we use in our subsequent analysis.Unlike past studies, which have relied almost exclusively on equity returns in the U.S.,our analysis includes returns in a wide range of asset markets.The data are available on diskette from the authors. Stocks and Bonds:Stock return data for the period 1960-1988 are drawn from Morgan Stanley's Capital International Perspectives (MSCI),augmented by data from Ibbotson Associates.For each of the thirteen equity markets in our sample--Australia, Austria,Belgium,Canada,France,Germany,Italy,Japan,Netherlands,Sweden,Switzer- land,United Kingdom,and United States-we calculate monthly excess returns R,.as R.=log (P..+D)-log (P..-1)-log (1+i) (1) where P.denotes the end-of-month price index for country j,D..dividend payments, and i,,the monthly short-term nominal interest rate.We chose these thirteen countries because they were the only ones in the Capital International universe with data back to 1960.The MSCI price index for each country is a weighted average of the prices for a number of large firms in the country's equity markets.These indices do not correspond to other published indices and often include shares traded on several different exchanges.? Our data on government bond returns are from Ibbotson Associates World Asser Module.Short-term yields are Treasury bill or money market yields,except in Italy, Sweden,and Switzerland,where we use the discount rate.The data sample for each country,for both bond and stock returns,is shown in Table 1.For comparability to earlier studies,we also report the results of autocorrelation tests applied to U.S.historical data from Ibbotson Associates (1988). Foreign Exchange:We compute the excess return to holding foreign currency assuming that investors making such investments hold foreign short-term bonds rather than cash.This implies that the excess return to a U.S.investor holding currency j is: Rts.=log (Eus./EUs..-1)+log (1+i )-log (1+ius.) (2) where the first term is the nominal appreciation of country i's currency relative to the dollar during month t.We focus on the returns to investors in each of five countries- France,Germany,Japan,the U.K.,and the U.S.-from holding the currencies of each of the other four countries.This yields 10 bilateral currency returns.Our sample period 1.MSCI computes dividend yields as aggregate dividends paid over the last twelve months divided by price at the end of the reference month.For several countries,dividend yields in the early part of the sample appear to reflect actual dividend payments rather than the sum of the previous year's payments.We adjusted these yields to make them comparable with the later sample.The resulting errors in the measured returns are likely to be smaller than those from omitting dividends altogether. 2.Poterba and Summers (1988)analyzed real (as distinct from excess)returns excluding dividends and computed from monthly averages of stock prices as reported by the International Monetary Fund. Copyright 2001 All Rights Reserved .....won
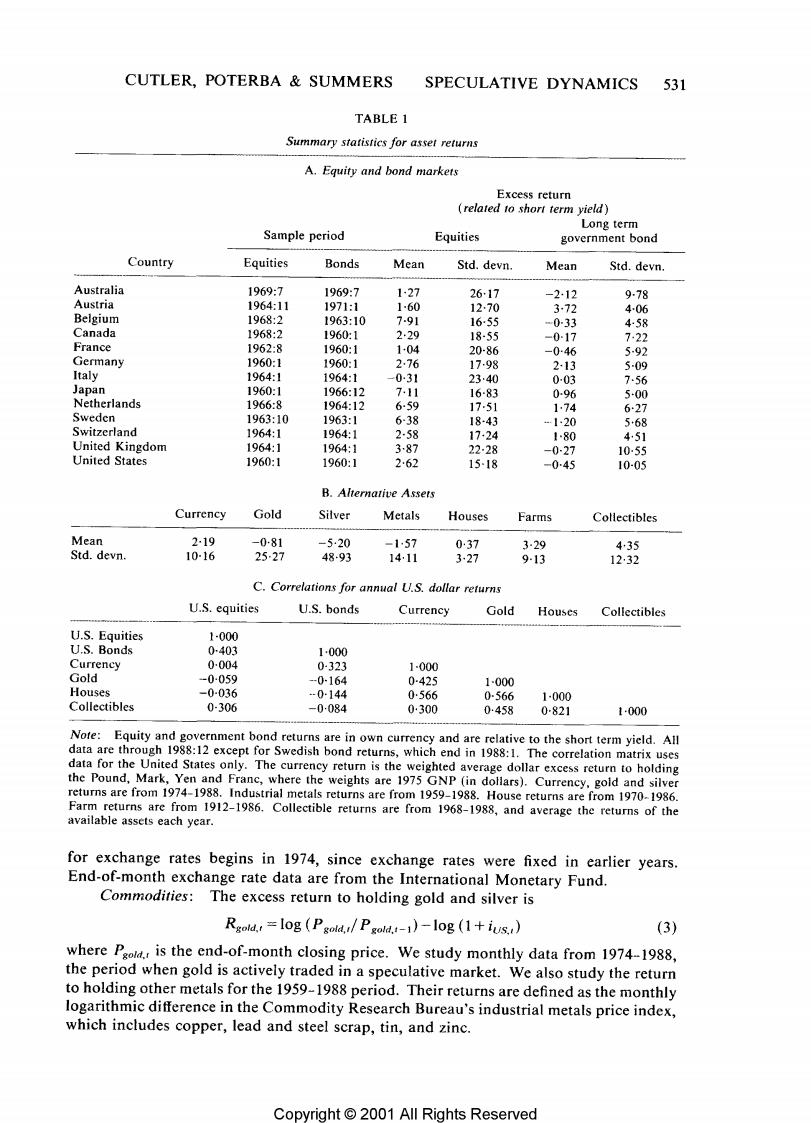
CUTLER,POTERBA SUMMERS SPECULATIVE DYNAMICS 531 TABLE 1 Summary statistics for asset returns A.Equity and bond markets Excess return related to short term yield) Long term Sample period Equities government bond Country Equities Bonds Mean Std.devn. Mean Std.devn. Australia 1969:7 1969:7 1-27 2617 -2.12 9-78 Austria 1964:11 1971:1 160 12.70 372 4-06 Belgium 1968:2 1963:10 791 16-55 -0-33 458 Canada 1968:2 1960:1 2·29 18-55 -017 722 France 1962:8 1960:1 1-04 20-86 -046 592 Germany 1960:1 1960:1 2.76 1798 213 5-09 Italy 1964:1 1964:1 -031 23.40 0-03 7.56 Japan 1960:1 1966:12 7,11 16-83 0-96 5-00 Netherlands 1966:8 1964:12 6-59 17-51 1.74 6·27 Sweden 1963:10 1963:1 6-38 18-43 1…20 568 Switzerland 1964:1 1964:1 2-58 17-24 1-80 451 United Kingdom 1964:1 1964:1 387 22-28 -0-27 1055 United States 1960:1 1960:1 262 15-18 -045 10-05 B.Alternative Assets Currency Gold Silver Metals Houses Farms Collectibles Mean 2-19 -081 -5·20 -157 037 3-29 435 Std.devn. 10-16 25-27 48-93 1411 327 9-13 12,32 C.Correlations for annual U.S.dollar returns U.S.equities U.S.bonds Currency Gold Houses Collectibles U.S.Equities 1-000 U.S.Bonds 0-403 1.000 Currency 0-004 0-323 1-000 Gold -0059 -0-164 0-425 1-000 Houses -0-036 -0-144 0566 0-566 1-000 Collectibles 0-306 -0084 0300 0:458 0-821 1-000 Note:Equity and government bond returns are in own currency and are relative to the short term yield.All data are through 1988:12 except for Swedish bond returns,which end in 1988:1.The correlation matrix uses data for the United States only.The currency return is the weighted average dollar excess return to holding the Pound,Mark,Yen and Franc,where the weights are 1975 GNP(in dollars).Currency,gold and silver returns are from 1974-1988.Industrial metals returns are from 1959-1988.House returns are from 1970-1986. Farm returns are from 1912-1986.Collectible returns are from 1968-1988,and average the returns of the available assets each year. for exchange rates begins in 1974,since exchange rates were fixed in earlier years. End-of-month exchange rate data are from the International Monetary Fund. Commodities:The excess return to holding gold and silver is Rgold.=log (Pgold./Pgold.-1)-log (1+ius.) (3) where Paold.,is the end-of-month closing price.We study monthly data from 1974-1988, the period when gold is actively traded in a speculative market.We also study the return to holding other metals for the 1959-1988 period.Their returns are defined as the monthly logarithmic difference in the Commodity Research Bureau's industrial metals price index, which includes copper,lead and steel scrap,tin,and zinc. Copyright 2001 All Rights Reserved

532 REVIEW OF ECONOMIC STUDIES Real Assets:We also analyze returns on houses and various collectibles.We measure excess holding returns under the assumption that these assets provide no service fow: R=l0g (P/P-1)-log (1+ius..). (4) Constant-quality house price indices are from Case and Shiller (1989).3 The data on collectibles,provided annually by Salomon Brothers for 1967-1988,cover oriental carpets, stamps,Chinese ceramics,rare books,coins,diamonds,and old master paintings. We also computed the return to holding farms by generalizing(4)to include a service flow term: Rfarm.=l0g Pfarm.!+Dfarm.)-log Pfarm.t-1)-log (1+ius.() (5) where Djarm.is aggregate farm income divided by aggregate farm value,then multiplied by the farm price index.The price is the average farm value per acre.Data on average value per are,1912-1986,were obtained from the Department of Agriculture (1981 and updates).Farm income data are from Colling and Irwin(1989). 2.AUTOCORRELATION OF ASSET RETURNS This section presents empirical evidence on the autocorrelation properties of asset returns. Analyzing many markets increases the statistical power of our tests,although in some cases the limited data span makes our findings relatively imprecise.The various markets should share any patterns that are common to the process of speculation,although risk considerations may differ across markets. Table I presents summary statistics on asset returns.The first panel focuses on equity and bond returns and shows substantial disparity in the mean returns across nations. Table 1 also shows the correlation between U.S.dollar returns on different classes of assets.The correlation between equity and bond returns is 0.403.The foreign exchange portfolio-a 1975 GNP-weighted average of the returns on the poind,franc,yen,and mark-exhibits a correlation of only 0-004 with U.S.equity returns,and its correlation with U.S.bond returns is 0.323.The real assets we analyze are highly correlated with each other,but negatively correlated with many other asset returns.Gold,houses and collectibles all exhibit cross-correlations of over 0.45,but the correlation between them and either stocks or bonds is small and usually negative.These findings suggest that our analysis of many different assets provides substantial evidence on the behaviour of speculative prices beyond that contained in equity returns. 2.1.The characteristic autocorrelogram of speculative returns Tables 2 through 4 present autocorrelograms for the various returns.We report the first order autocorrelation as well as the average autocorrelation over several distinct twelve month intervals.In each case,the reported autocorrelations have been corrected for small sample bias as described in the appendix. Table 2 presents the autocorrelations for stocks and bonds,Table 3 for foreign exchange and precious metals,and Table 4 for real assets.When we analyse data from 3.In order to avoid autocorrelation induced by measurement error,Case and Shiller formed an A and B price index for each city,using separate houses in each index.Our autocorrelations correlate contemporaneous values of the A series with lags of the B series.The results are very similar when the two series are reversed. www Copyright o 2001 All Rights Reserved

CUTLER,POTERBA SUMMERS SPECULATIVE DYNAMICS 533 TABLE 2 Autocorrelations for stock and bond returns Autocorrelations-excess returns relative to short-term treasury bills Months averaged in autocorrelations Asset 1-12 13-24 25-36 37-48 49-60 61-72 73-84 85-96 Corporate equities (1960-1988) Australia 0-028 0-002 -0-022 0-007 0012 0-003 -0-013 0-004 0-034 Austria 0-116 0-070 -0040 -0-002 -0007 -0-024 0-007 0-012 -0-014 Belgium 0-200 0-018 0006 0-040 0-009 0-016 -0022 0-033 -0-014 Canada 0-057 0-002 -0032 -0-004 0-G07 0-007 -0014 0-019 0039 France 0-083 0007 -0021 0-023 0-003 0-000 -0001 0-030 0-022 Germany 0-138 0-029 -0-042 0-002 0-006 -0-003 -0024 -0-003 0-044 Italy 0-138 0044 -0-040 0-000 -0017 0019 0-031 -0-013 0-031 Japan 0-085 0020 -0025 0019 0-004 -0-016 0-010 0-017 -0-013 Netherlands 0-114 0-021 -0015 0-004 0-010 0-002 -0-022 -0005 0-036 Sweden 0-134 0-038 -0041 0-022 0-001 0000 0-002 -0011 0-035 Switzerland 0046 0-017 -0019 -0-017 0-020 -0-007 -0019 0-008 0022 U.K. 0-091 0002 -0015 -0015 0011 0009 -0005 0-010 0-019 U.S. 0-077 -0-002 -0029 0004 0-017 0-019 -0016 0-000 0-041 Average 0-101 0021 -0-026 0-006 0-006 0-019 -0007 0-008 0-022 (0-030) (0-004) (0-0091 (0-006) (0-014) (0-016) (0-008) (0-011) (0-005) United States 0-106 0-021 -0-017 -0005 -0-011 -0006 0-000 0-012 0-013 (1926-1988) (0-036) (0011) (0011) (0-011) (0011) (0-011) (0011) (0-011) (0-011) Long-term bonds (1960-1988) Australia 0-078 0-036 -0-013 -0-032 -0-010 0012 0014 0022 0-008 Austria 0-360 0-119 -0-046 -0-067 -0003 0-013 -0-010 0-060 0-056 Belgium 0-191 0-110 0-006 -0-005 -0006 -0-023 -0-022 0-025 0012 Canada 0116 0-032 -0-008 -0-007 -0015 -0-020 0011 0-002 0-004 France 0230 0-086 -0-009 -0011 -0012 -0039 0-004 -0-003 0047 Germany 0477 0-106 -0-033 -0-041 -0-055 -0029 -0024 0003 0-051 Italy 0514 0-115 -0-003 -0-026 -0049 0018 -0018 0-078 -0010 Japan 0-132 0-062 -0-028 -0-036 -0-024 0024 0056 0-008 -0032 Netherlands 0291 0-043 -0-026 -0-017 -0015 0-013 -0-001 0-006 0023 Sweden 0-116 -0007 0-004 -0-006 -0015 0031 0-008 0-004 -0006 Switzerland 0-266 0-083 -0010 -0-045 -0-014 -0020 0-030 -0-012 0-010 U.K. 0-299 0-026 0-003 -0-039 -0014 0-031 0-036 0017 0-006 U.S. 0-030 0027 -0012 -0-005 0-008 -0-016 0-000 -0006 -0-003 Average 0-238 0-064 -0013 -0026 -0-017 -0-002 0-006 0-012 0013 (0-015) (0-004) (0-005) (0005) (0-005) (0005) (0-005) (0-005) (0-005) United States 0033 0023 -0-010 0-001 0-009 -0010 0-004 0-000 0-000 (1926-1988) (0036) (0011) (0011) (0-011) (0-011)(0-011)(0-011) (0011) (0-011) Note.Each entry reports the average autocorrelation for the 1 or 12 months in the indicated time period.The autocorrelations are bias-adjusted,by adding 1/(T-j)to each entry,where T is the length of the time period, andJ is the autocorrelation.The standard error of the individual correlations is (T-k)s,as in Kendall (1973).The standard error of the average autocorrelation,shown in parentheses,adjusts the predicted standard error for the cross-correlation of the assets,as indicated in the text. several countries,we also report the average autocorrelation at each frequency.We view this as a summary indication of the autocorrelation pattern,not as a deep parameter which characterizes behaviour in all markets.To indicate the precision of this average, we calculate its standard error assuming that the estimated statistics(such as the average of twelve autocorrelations)exhibit a constant pairwise correlation across countries, Copyright 2001 All Rights Reserved
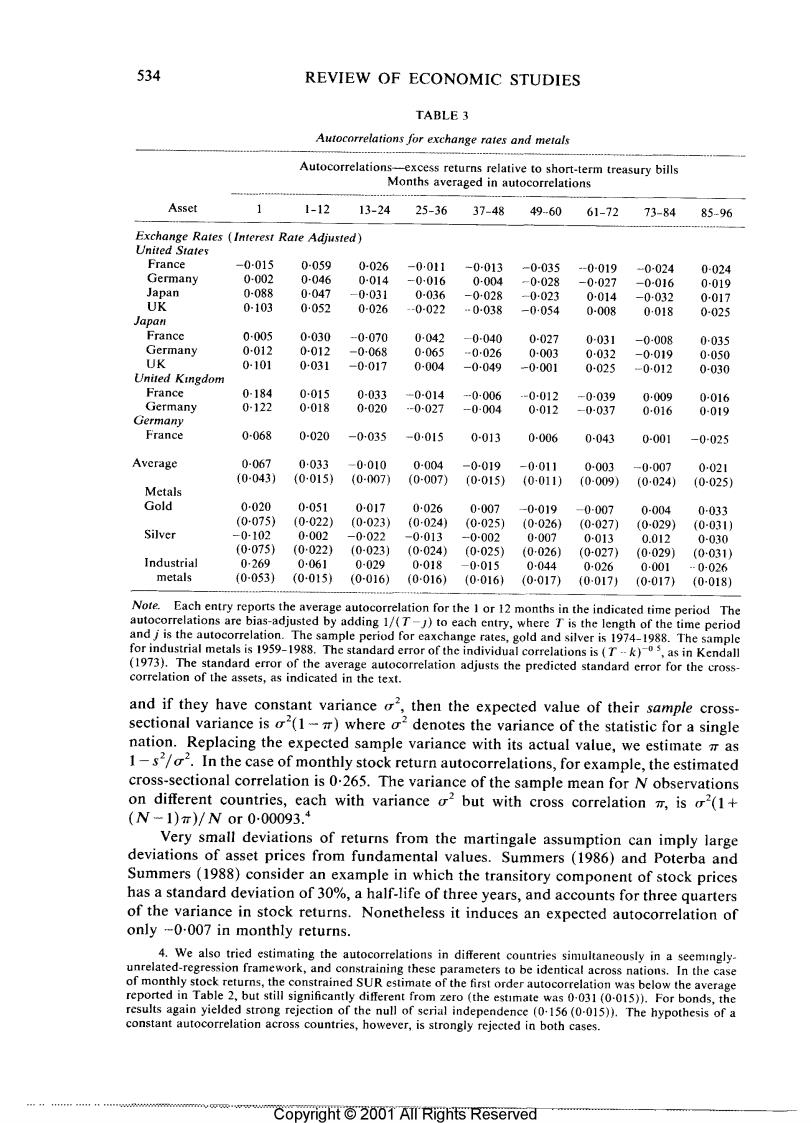
534 REVIEW OF ECONOMIC STUDIES TABLE 3 Autocorrelations for exchange rates and metals Autocorrelations-excess returns relative to short-term treasury bills Months averaged in autocorrelations Asset 1-12 13-24 25-36 37-48 49-60 61-72 73-84 85-96 Exchange Rates (Interest Rate Adjusted) United States France -0-015 0-059 0-026 -0011 -0-013 -0-035 -0-019 0-024 0-024 Germany 0-002 0046 0-014 -0016 0-004 -0028 -0027 -0-016 0-019 Japan 0-088 0047 -0-031 0-036 -0028 -0023 0014 -0-032 0017 UK 0-103 0052 0-026 -0-022 …0038 -0054 0-008 0-018 0-025 Japan France 0-005 0-030 -0-070 0-042 -0-040 0-027 0031 -0-008 0035 Germany 0-012 0-012 -0-068 0-065 -0-026 0-003 0-032 -0-019 0050 UK 0-101 0-031 -0-017 0-004 -0-049 -0-001 0025 -0012 0-030 United Kingdom France 0-184 0015 0-033 -0-014 -0-006 -0012 -0039 0009 0-016 Germany 0-122 0018 0-020 -0-027 -0-004 0-012 -0-037 0016 0-019 Germany France 0-068 0-020 -0-035 -0015 0013 0-006 0-043 0-001 -0-025 Average 0-067 0·033 -0-010 0-004 -0019 -0011 0-003 -0-007 0021 (0-043) (0-015) (0-007) (0007) (0-015) (0-011) (0-009) (0024) (0-025) Metals Gold 0-020 0-051 0017 0026 0-007 -0-019 -0-007 0-004 0-033 (0075 (0-022) (0-023 (0-024) (0-025) (0-026) (0-027) (0-029) (0-0311 Silver -0-102 0-002 -0-022 -0-013 -0002 0-007 0-013 0.012 0-030 (0-075 (0022) (0-023) (0024) (0025) (0-026) (0027) (0029) (0-031) Industrial 0269 0061 0-029 0-018 -0015 0044 0-026 0001 -0-026 metals (0-053) (0-015) (0-016) (0016) (0016) (0-017)0-0171 (0017) (0-018) Note.Each entry reports the average autocorrelation for the 1 or 12 months in the indicated time period The autocorrelations are bias-adjusted by adding 1/(T-J)to each entry,where T is the length of the time period and j is the autocorrelation.The sample period for eaxchange rates,gold and silver is 1974-1988.The sample for industrial metals is 1959-1988.The standard error of the individual correlations is (Tk),as in Kendall (1973).The standard error of the average autocorrelation adjusts the predicted standard error for the cross- correlation of the assets,as indicated in the text. and if they have constant variance o",then the expected value of their sample cross- sectional variance is o2(1)where o2denotes the variance of the statistic for a single nation.Replacing the expected sample variance with its actual value,we estimate m as 1-s2/o2.In the case of monthly stock return autocorrelations,for example,the estimated cross-sectional correlation is 0.265.The variance of the sample mean for N observations on different countries,each with variance o2 but with cross correlation m,is (1+ (N-1)π)/Nor000093.4 Very small deviations of returns from the martingale assumption can imply large deviations of asset prices from fundamental values.Summers (1986)and Poterba and Summers (1988)consider an example in which the transitory component of stock prices has a standard deviation of 30%,a half-life of three years,and accounts for three quarters of the variance in stock returns.Nonetheless it induces an expected autocorrelation of only -0-007 in monthly returns. 4.We also tried estimating the autocorrelations in different countries simultaneously in a seemingly- unrelated-regression framework,and constraining these parameters to be identical across nations.In the case of monthly stock returns,the constrained SUR estimate of the first order autocorrelation was below the average reported in Table 2,but still significantly different from zero (the estimate was 0-031(0-015)).For bonds,the results again yielded strong rejection of the null of serial independence (0-156(0-015)).The hypothesis of a constant autocorrelation across countries,however,is strongly rejected in both cases. Copyright 2001 All Rights Reserved
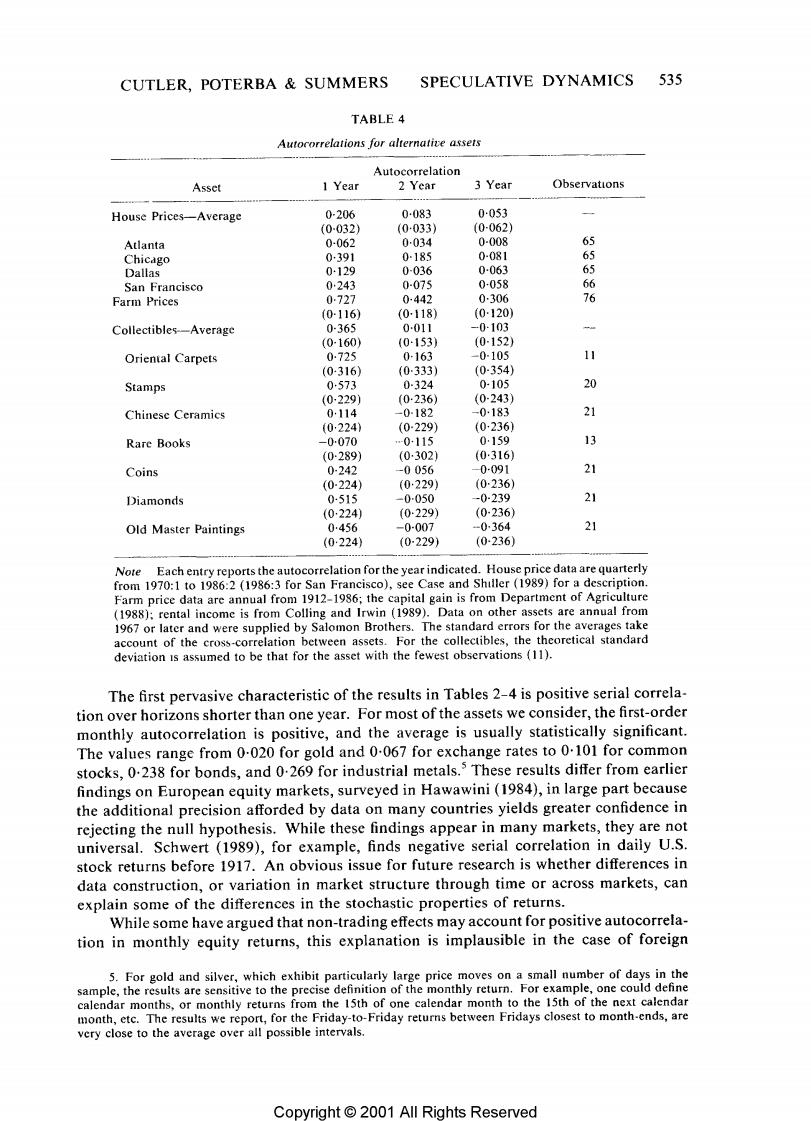
CUTLER,POTERBA SUMMERS SPECULATIVE DYNAMICS 535 TABLE 4 Autocorrelations for alternatice assets Autocorrelation Asset 1 Year 2 Year 3 Year Observations House Prices-Average 0-206 0-083 0053 (0-032) (0033) (0-062) Atlanta 0-062 0034 0-008 65 Chicago 0391 0-185 0-081 65 Dallas 0-129 0-036 0-063 65 San Francisco 0243 0-075 0-058 66 Farm Prices 0-727 0-442 0-306 76 (0-116) (0-118) (0120) Collectibles--Average 0-365 0011 -0-103 (0-160) (0-153) (0-152) Oriental Carpets 0725 0-163 -0-105 11 (0-316) (0333) (0-354) Stamps 0573 0-324 0-105 20 (0229j (0-236) (0-243) Chinese Ceramics 0114 -0-182 -0183 (0224) (0229) (0-236) Rare Books -0-070 0-115 0159 13 (0289) (0302) (0-316) Coins 0-242 -0056 0-091 21 (0-224) (0·229) (0236) Diamonds 0-515 -0-050 -0-239 21 (0224) (0229) (0-236) Old Master Paintings 0456 -0-007 -0364 21 (0:224) (0-229) (0236) Note Each entry reports the autocorrelation for the year indicated.House price data are quarterly from 1970:1 to 1986:2 (1986:3 for San Francisco),see Case and Shiller (1989)for a description. Farm price data are annual from 1912-1986;the capital gain is from Department of Agriculture (1988);rental income is from Colling and Irwin (1989).Data on other assets are annual from 1967 or later and were supplied by Salomon Brothers.The standard errors for the averages take account of the cross-correlation between assets.For the collectibles,the theoretical standard deviation is assumed to be that for the asset with the fewest observations (11). The first pervasive characteristic of the results in Tables 2-4 is positive serial correla- tion over horizons shorter than one year.For most of the assets we consider,the first-order monthly autocorrelation is positive,and the average is usually statistically significant. The values range from 0-020 for gold and 0.067 for exchange rates to 0.101 for common stocks,0.238 for bonds,and 0.269 for industrial metals.These results differ from earlier findings on European equity markets,surveyed in Hawawini(1984),in large part because the additional precision afforded by data on many countries yields greater confidence in rejecting the null hypothesis.While these findings appear in many markets,they are not universal.Schwert (1989),for example,finds negative serial correlation in daily U.S. stock returns before 1917.An obvious issue for future research is whether differences in data construction,or variation in market structure through time or across markets,can explain some of the differences in the stochastic properties of returns. While some have argued that non-trading effects may account for positive autocorrela- tion in monthly equity returns,this explanation is implausible in the case of foreign 5.For gold and silver,which exhibit particularly large price moves on a small number of days in the sample,the results are sensitive to the precise definition of the monthly return.For example,one could define calendar months,or monthly returns from the 15th of one calendar month to the 15th of the next calendar month,etc.The results we report,for the Friday-to-Friday returns between Fridays closest to month-ends,are very close to the average over all possible intervals. Copyright 2001 All Rights Reserved

536 REVIEW OF ECONOMIC STUDIES exchange,gold or bonds.Even in the case of equities,our focus on monthly data makes non-trading biases unlikely;Lo and McKinlay (1988)find little support for non-trading as the explanation of positive autocorrelation in weekly U.S.equity returns since 1962. The estimated monthly autocorrelations are not only statistically but also substantively significant,often implying negative expected returns.If the monthly risk premium in a given market is u,the ex ante risk premium on an asset will be negative if pR,<-u, which occurs with probability (-u/p )where is the distribution function for returns For stocks,if one takes the risk premium to be 0.7%per month and the standard deviation of returns to be 5%per months,negative expected returns would be observed more than 10%of the time.For bonds,where the standard deviation is only slightly smaller but the risk premium is much smaller,the calculation is even more dramatic. Substantial autocorrelation at short horizons is particularly difficult to reconcile with traditional asset-pricing models.As we expand the return interval,the risk premium increases linearly while the standard deviation of returns rises with the square root of the interval length.For k-period returns,therefore,the chance of a negative expected return is(-k/p),where p is the autocorrelation coefficient for this horizon.The probability of a negative expected return is therefore higher if an autocorrelation coefficient of a given absolute value is observed at high frequencies. Positive autocorrelation is not confined to one-month returns.By subtracting one- twelfth of the first month's autocorrelation from the average autocorrelation over the (1-12)-month interval,one finds that average autocorrelations between two and twelve months are positive for all of the assets.For equities,the one-month autocorrelation is 0.101 and the average over the next eleven months is 0-013.For bonds,the corresponding values are 0.238 and 0-047,while for foreign exchange the average autocorrelation at months 2-12 is 0-029.For both stocks and bonds,markets in the United States exhibit below-average degrees of positive autocorrelation.These findings strengthen earlier results (for example Poterba and Summers (1988)and Lo and MacKinlay (1988))of positive serial correlation in U.S.equity returns. For collectibles,farms,and real estate,data limitations prevent us from calculating monthly return autocorrelations.Nevertheless,the returns on these assets show positive serial correlation at an annual frequency.For house prices,the annual autocorrelation averages 0-206 for the four cities,while for farm returns and collectibles,the autocorrela- tions are even larger. The results in Tables 2-4 also suggest the presence of negative autocorrelation at longer lags,although the evidence on this point is less compelling than that for positive high-frequency autocorrelation.For both stocks and bonds,the average of the 13th-24th autocorrelations is statistically significantly negative.The correlation is also negative in U.S.historical data on equity returns.For bonds,the negative serial correlation persists, with negative average autocorrelations at twelve-month windows up to 60 months.For exchange rates,the average autocorrelation in the second year is negative and approxi- mately equal to its standard error,paralleling earilier findings by Huizinga(1986).The 6.At higher frequencies,for example in daily returns,there may be non-trading biases even in recent years,when stock exchange volume has been far higher than in earlier decades.For the period since 1982, when S&P futures contracts have been traded,daily and weekly returns on the S&P 500 index exhibit more positive autocorrelation than the analogous futures returns.The interpretation of this result is tempered, however,by the finding that the difference between spot and futures prices forecasts index returns no better than returns on S&P futures. 7.The negative autocorrelations for stocks during the post-1960 period are noteworthy,since Kim,Nelson and Startz (1989)and others have emphasized the sensitivity (noted in Poterba and Summers(1988))of evidence for mean-reversion in U.S.stock prices to inclusion of the Depression period. Copynight 2001 All Rights ReservedR

CUTLER,POTERBA SUMMERS SPECULATIVE DYNAMICS 537 negative autocorrelation is somewhat more pronounced at longer lags.There is also more pronounced evidence of negative autocorrelation at longer lags,notably between three and four years.There is little evidence of negative autocorrelation in the returns to holding metals,houses,or farmland,although Case and Shiller (1990)present evidence that annual real returns in the housing market are negatively autocorrelated at longer horizons. 3.PREDICTING RETURNS USING INFORMATION ON FUNDAMENTALS The previous results suggest that asset returns are partly predictable on the basis of lagged returns.In this section,we examine the extent to which returns over various horizons can be forecast using information on the deviation of price from estimates of fundamental value,as well as lagged values of short-term interest rates. 3.1.The predictive power of fundamentals We begin by examining whether the deviation between actual prices and crude proxies for fundamental values have forecast power for returns.We study returns over horizons of one,twelve,and forty-eight months by estimating regression equations of the form: T+k=ak+Bk(Z,-p)+”+k (6) where r+k is the return from period t to period t+k and(z,-p,)is the difference between the logarithm of a potentially noisy measure of fundamental value (z)and the asset price.We interpret Bx as the fraction of the deviation from the price fundamental which is eradicated over a k-month horizon.If the current market price is one percent below the price fundamental z,then returns over the next month will be higher by 0.01B. To test the null hypothesis that returns are unpredictable,we compute the bias- corrected t-statistic for B&using Newey-West (1987)standard errors.(The bias correction is described in the appendix.)We also use Monte Carlo simulations to find the empirical distribution of the t-statistic of B&under the null hypothesis.We report the p-value associated with the hypothesis that the bias-corrected f-statistic equals zero. Imprecise measures of price fundamentals will bias our tests against finding that the divergence between price and the measured fundamental can forecast returns.Neverthe- less,under the null hypothesis that asset returns cannot be predicted using lagged information,none of our variables should exhibit any forecast power. For equities,we measure the price fundamental as a constant multiple of the real dividend.The variable(z,-p,)is therefore the logarithm of the dividend-price ratio,and equation (6)resembles equations estimated by Campbell and Shiller (1988)and Fama and French(1988).In the bond market,the efficient markets hypothesis and the assump- tion of a constant risk premium imply that the long-term interest rate is a weighted average of expected future short-term rates.If short rates are a random walk,the long rate should equal the short rate,and the fundamental value of the long-term bond is therefore the reciprocal of the short rate.Since the actual price of the long-term bond is the reciprocal of the long rate,we define (z,-p)as the logarithm of the long rate divided by the short rate.The resulting specification resembles the term structure tests of Shiller,Campbell and Schoenholtz (1983)and Mankiw and Summers (1984). The fundamental value of the exchange rate depends on the long-run real exchange rate at which a sustainable trade balance can be achieved.Rather than attempting to 8.Hodrick (1990)and Nelson and Kim(1990)discuss the potential biases in estimating equations similar to (6),and present Monte Carlo evidence using a somewhat different specification of the null hypothesis. Copyright 2001 All Rights Reserved

538 REVIEW OF ECONOMIC STUDIES model changes in terms of trade,we simply assume that the real exchange rate consistent with long-run trade balance is a constant.The logarithmic difference between the funda- mental and the current exchange rate is therefore just minus the logarithm of the real exchange rate.We use the same approach with metals,so the price deviation is minus the logarithm of the real price. Table 5 presents evidence on the forecast power of differences between fundamentals and prices in world equity markets.The first column considers the forecastability of one month returns;the results are relatively weak.The estimated coefficient on z,-p,has a p-value less than 0.10 for only three of the thirteen countries,although the cross-country average (reported in the penultimate row)has a p-value of 0-02.The point estimates, however,suggest substantively important links between the dividend-price ratio and subsequent returns.The average value of B,,0-75,implies that the ex ante risk premium is negative whenever dividend yields are less than approximately forty percent below their average value.It also suggests that about three-quarters of one percent of any deviation between the current price and our dividend-based fundamental is corrected in the first month after such a deviation appears. The centre columns in Table 5 report regressions for twelve-month returns.The patterns of coefficients is similar to the one-month returns.On average,approximately 15%of a deviation from the price fundamental is erased over the subsequent year.Since the average value of B2 is about seventeen times the average for B,the evidence suggests that the dividend-price ratio's forecast power for one-period returns grows slightly as the horizon grows.In four of the thirteen countries,the coefficient has a p-value less than 010;the p-value for the average,however,is 001.The most notable outlier is Japan, where the coefficient is negative and statistically significant.For the United States,the forecast power of the dividend-price ratio appears to have fallen over time.Within our post-1960 sample,however,there is limited evidence of parameter instability.We experi- mented by allowing for a parameter shift in the middle of our data sample,and in nine of the thirteen stock markets we analyze,the null hypothesis of parameter constancy was not rejected at standard levels. The final columns in Table 5 present evidence for 48-month returns.Although the sample size for these regressions is limited,the results suggest some predictive power of dividend-price ratios.The average correction to deviations between the current price and our simple measure of fundamentals is forty-one percent over a four-year horizon.This confirms Fama and French's(1988)earlier findings based on U.S.time-series data. These results are nevertheless much weaker than might have been expected in light of earlier findings for the United States.These discrepancies may be attributed to several features.First,our corrections for small-sample bias significantly reduce the average 9.We also experimented with allowing the fundamental value for equities,exchange rates,and metals to vary with the long term real interest rate The qualitative conclusions were similar to those we report below, although this modification typically raised the standard errors of our estimated coefficients. 10.We also applied the seemingly-unrelated-regression methodology,constraining the coefficient on the dividend-price ratio to be the same across all nations.In this framework we did not calculate Newey-West standard errors or make out small-sample adjustment,but the results may nevertheless be of interest.If the twelve-month equations are estimated by OLS,the resulting average coefficient is 24.23 and our cstimated standard error for the average is 294.Constraining the B2 parameter to be identical across countries yields a value of 15.62(0-84),strongly rejecting the null hypothesis of no effect.The data also reject the hypothesis of a common coefficient,however. 11.The power of the dividend-price ratio to forecast U.S.multiperiod returns is only slightly smaller for the post-1945 period than for the 1926-1988 period,in contrast to the finding of long-horizon negative serial correlation in returns,which is much weaker for the latter period.However,for the period since 1960,shown in Table 5,the forecast power of dividend-price ratios is distinctly lower than in the longer sample. Copyright 2001 All Rights Reserved