
第十章协方差分析 第十章协方差分析 教学要求: 1、了解协方差分析的意义。 2、掌握单因子协方差分析的基本步骤
第十章 协方差分析 教学要求: 2、掌握单因子协方差分析的基本步骤。 1、了解协方差分析的意义。 第十章 协方差分析

第十章 协方差分析 第一节协方差分析的意义 试验控制 为了提高试验的精确性和准确性,对处理以外 的一切条件都需要采取有效措施,使它们在各处理 间尽量一致,这叫试验控制。 例如:研究几种饲料对猪的增重效果,要求供试仔 猪的初始重相同,因为仔猪的初始重不同,会影响猪的 增重效果
第一节 协方差分析的意义 为了提高试验的精确性和准确性,对处理以外 的一切条件都需要采取有效措施,使它们在各处理 间尽量一致,这叫试验控制。 一、试验控制 第十章 协方差分析 例如:研究几种饲料对猪的增重效果,要求供试仔 猪的初始重相同,因为仔猪的初始重不同,会影响猪的 增重效果
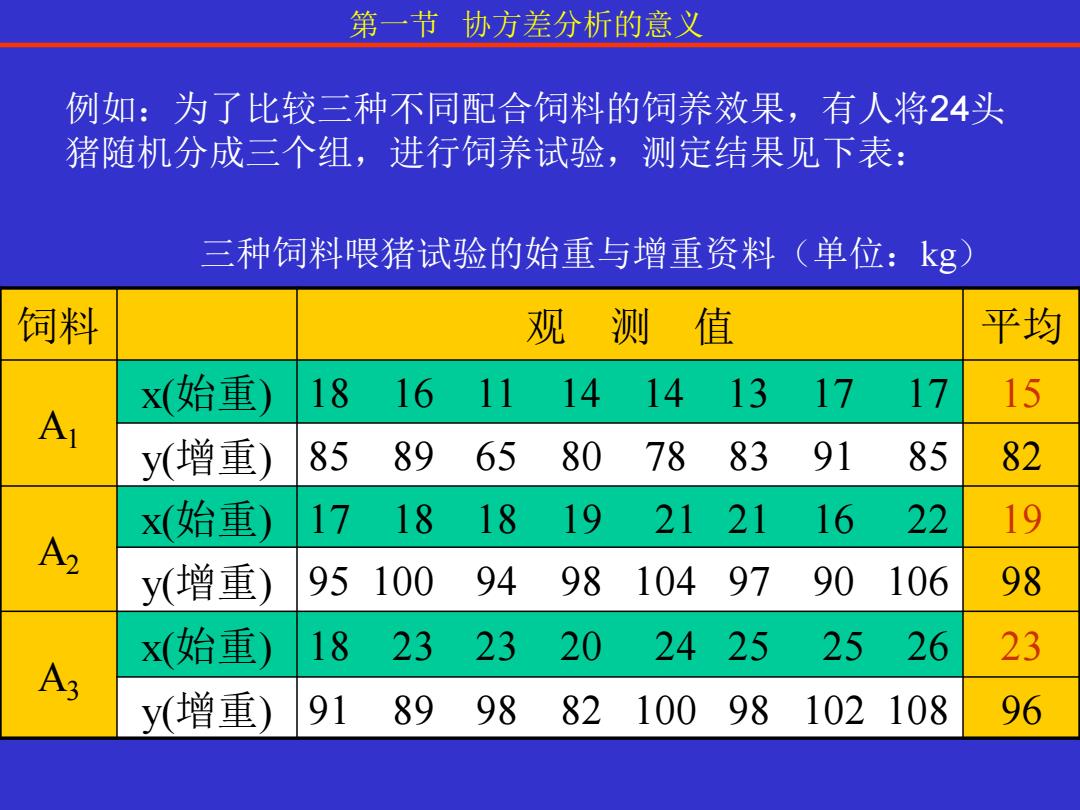
第一节协方差分析的意义 例如:为了比较三种不同配合饲料的饲养效果,有人将24头 猪随机分成三个组,进行饲养试验,测定结果见下表: 三种饲料喂猪试验的始重与增重资料(单位:kg〉 饲料 观测值 平均 x(始重) 181611 14 1413 17 17 15 A y(增重) 858965 807883 91 85 82 x(始重) 171818 19 2121 16 22 19 A2 y(增重) 95100 94 98104 97 90106 98 x(始重) 18 23 23 20 2425 2526 23 A3 y(增重) 91 89 98 82100 98102108 96
例如:为了比较三种不同配合饲料的饲养效果,有人将24头 猪随机分成三个组,进行饲养试验,测定结果见下表: 饲料 观 测 值 平均 A1 x(始重) 18 16 11 14 14 13 17 17 15 y(增重) 85 89 65 80 78 83 91 85 82 A2 x(始重) 17 18 18 19 21 21 16 22 19 y(增重) 95 100 94 98 104 97 90 106 98 A3 x(始重) 18 23 23 20 24 25 25 26 23 y(增重) 91 89 98 82 100 98 102 108 96 三种饲料喂猪试验的始重与增重资料(单位:kg) 第一节 协方差分析的意义

第一节协方差分析的意义 二、统计控制 在实际试验中,很难满足供试仔猪初始体重完全相 同的条件。 如果仔猪的初始重(x)与增重(记为y)存在回归关 系,则可以应用统计学方法将仔猪增重矫正为初始 重相同时的增重,在消除初始重不同对仔猪增重的 影响后,再进行方差分析,这叫试验控制。 通过矫正,试验误差将减少,对试验处理的效应估计 将更为准确
如果仔猪的初始重(x)与增重(记为y)存在回归关 系,则可以应用统计学方法将仔猪增重矫正为初始 重相同时的增重,在消除初始重不同对仔猪增重的 影响后,再进行方差分析,这叫试验控制。 二、统计控制 第一节 协方差分析的意义 通过矫正,试验误差将减少,对试验处理的效应估计 将更为准确。 在实际试验中,很难满足供试仔猪初始体重完全相 同的条件

第一节协方差分析的意义 三、协方差分析定义 将回归分析与方差分析结合起来的统计方法, 叫作协方差分析(analysis of covariance) 四、适用范围 协方差分析适用于:两变数间存在显著的回归关系而 初值不一致的资料
将回归分析与方差分析结合起来的统计方法, 叫作协方差分析(analysis of covariance) 三、协方差分析定义 四、适用范围 协方差分析适用于:两变数间存在显著的回归关系而 初值不一致的资料。 第一节 协方差分析的意义

第一节协方差分析的意义 五、协方差组分的估计 ∑(x-x)y-y) V∑(x-x)2(y-y)2 分子、分母同时除以自由度(n-1),得 ∑(x-x)(y-y)(n-1) V∑(x-x)2/(n-1)V∑y-y)2/(n-1)
五、协方差组分的估计 第一节 协方差分析的意义 − − − − = 2 2 ( ) ( ) ( )( ) x x y y x x y y r 分子、分母同时除以自由度(n-1),得 ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r

第一节协方差分析的意义 ∑(x-xy-y)/(n-1) V∑(x-x)2/(n-1)V∑(y-y)2/(n-1) 其中, ∑(x-x)2 是×的均方MSx,是×的总体方差 的无偏估计量。 n-1 ∑y-y)2 2 是y的均方MSy,是y的总体方差 的无偏估计量。 n-1 ∑(x-xy-y) 是×与y的离均差的乘积和,简称均积,记为 n-1 大与均积相对应的总体参数叫协方差,记为COV(x,y) 大均积是协方差的无偏估计量,即EMP,=COV(x,y)
第一节 协方差分析的意义 其中, ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r 1 ( ) 2 − − n x x 1 ( ) 2 − − n y y 1 ( )( ) − − − n x x y y 是x的均方MSx,是x的总体方差 的无偏估计量。 2 x 2 是y的均方MS y y,是y的总体方差 的无偏估计量。 是x与y的离均差的乘积和,简称均积,记为 ★与均积相对应的总体参数叫协方差,记为 COV(x, y) MPxy ★均积是协方差的无偏估计量,即 EMP COV(x, y) xy =

第一节协方差分析的意义 ∑(x-x(y-y)/(n-1) 正法显示该图 ∑(x-x2n-1V∑少-丹2(-1) 于是,相关系数可以表示为: MP MS,MS, 相应的总体相关系数可以表示为: COV(x,y) 00y OxOy
第一节 协方差分析的意义 于是,相关系数可以表示为: ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r x y xy MS MS MP r = 相应的总体相关系数可以表示为: x y xy x y COV x y = = ( , )

第一节协方差分析的意义 大均积与均方具有相似的形式,也有相似的性质 无法显示该图片 大方差分析时,一个变量的总平方和与自由度可按变 异来源进行剖分,进而求得相应的均方。 大同样,两个变量的总乘积和自由度也可按变异来源 进行剖分,从而获得相应的均积。 把两个变量的总乘积和与自由度按变异来 源进行剖分,并获得相应的均积的方法,也称为 协方差分析
第一节 协方差分析的意义 ★均积与均方具有相似的形式,也有相似的性质。 ★方差分析时,一个变量的总平方和与自由度可按变 异来源进行剖分,进而求得相应的均方。 ★同样,两个变量的总乘积和自由度也可按变异来源 进行剖分,从而获得相应的均积。 把两个变量的总乘积和与自由度按变异来 源进行剖分,并获得相应的均积的方法,也称为 协方差分析
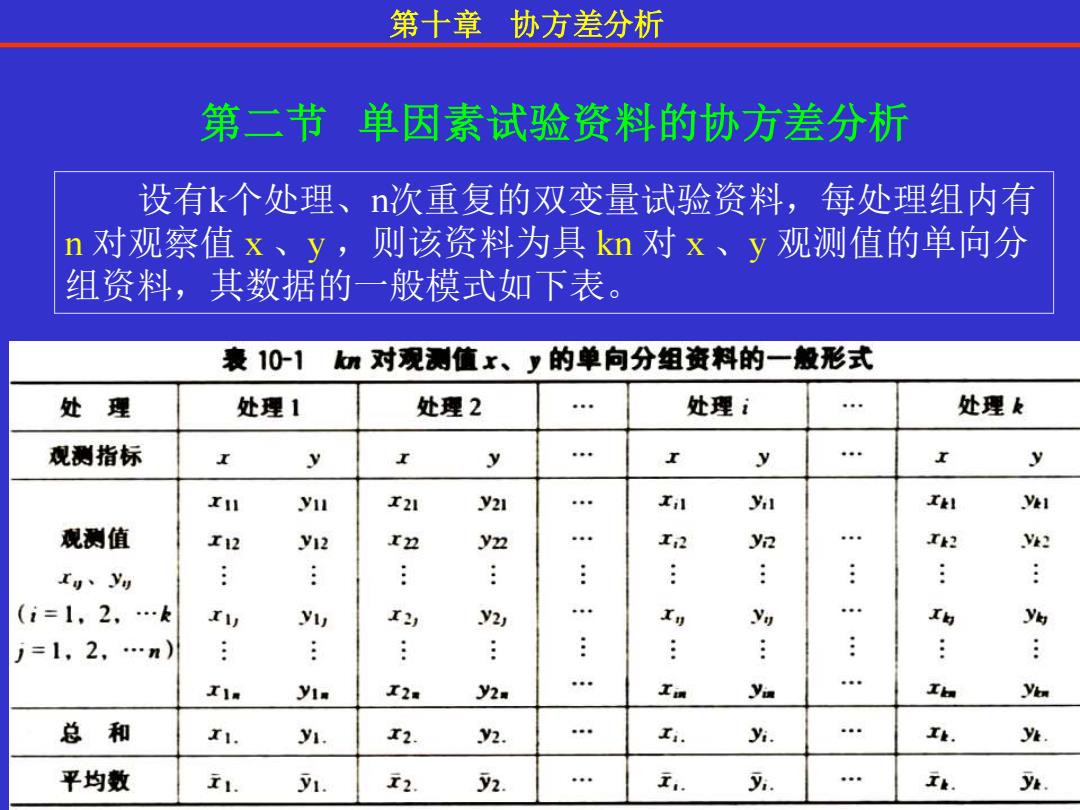
第十章协方差分析 第三节单因素试验资料的协方差分析 设有k个处理、次重复的双变量试验资料,每处理组内有 n对观察值x、y,则该资料为具kn对x、y观测值的单向分 组资料,其数据的一般模式如下表。 表101对观测值x、y的单向分组资料的一般形式 处理 处理1 处理2 .. 处理i 处理k 观测指标 y 。年 y . y xn y11 I21 y21 Jil y ZH y:1 观测值 x12 y12 In yn In y2 TH2 : rg、yg (i=1,2、…k I\ y 12 y2, Iy g Ik yh j=1,2,…n) x1. y1. I2s y2m 工m yin Ih yin 总和 r1. y1. x2. 2. Ii. yi. Ik. % 平均数 i1. y1. r2. y2. 000 工. Bi. 年0 Ih
第二节 单因素试验资料的协方差分析 第十章 协方差分析 设有k个处理、n次重复的双变量试验资料,每处理组内有 n 对观察值 x 、y ,则该资料为具 kn 对 x 、y 观测值的单向分 组资料,其数据的一般模式如下表