
第一节:统计学习与推理基础 00M队 Fisher经典参数统计理论 Fisher把判别分析、回归分析和和密度估计问题等表达为特定参数化模型 的参数估计问题,并提出了估计所有模型未知参数的方法一一最大似然法。 2
Fisher经典参数统计理论 第一节:统计学习与推理基础 2 Fisher把判别分析、回归分析和和密度估计问题等表达为特定参数化模型 的参数估计问题,并提出了估计所有模型未知参数的方法——最大似然法
第一节:统计学习与推理基础 000 、经验非线性方法 人工神经网络(artificial neural network,ANN)具有很好的非线性逼近能 力,克服了经典参数统计理论中参数估计方法的困难,但存在模型结构难 以确定(缺乏一种统一的数学理论,更多地依赖于使用者的技巧)、可解 释性差(没有一个显性的表达式)、易于出现过度训练和训练不足、陷入 局部最小等诸多缺陷 6 5 ●D 4 ① D
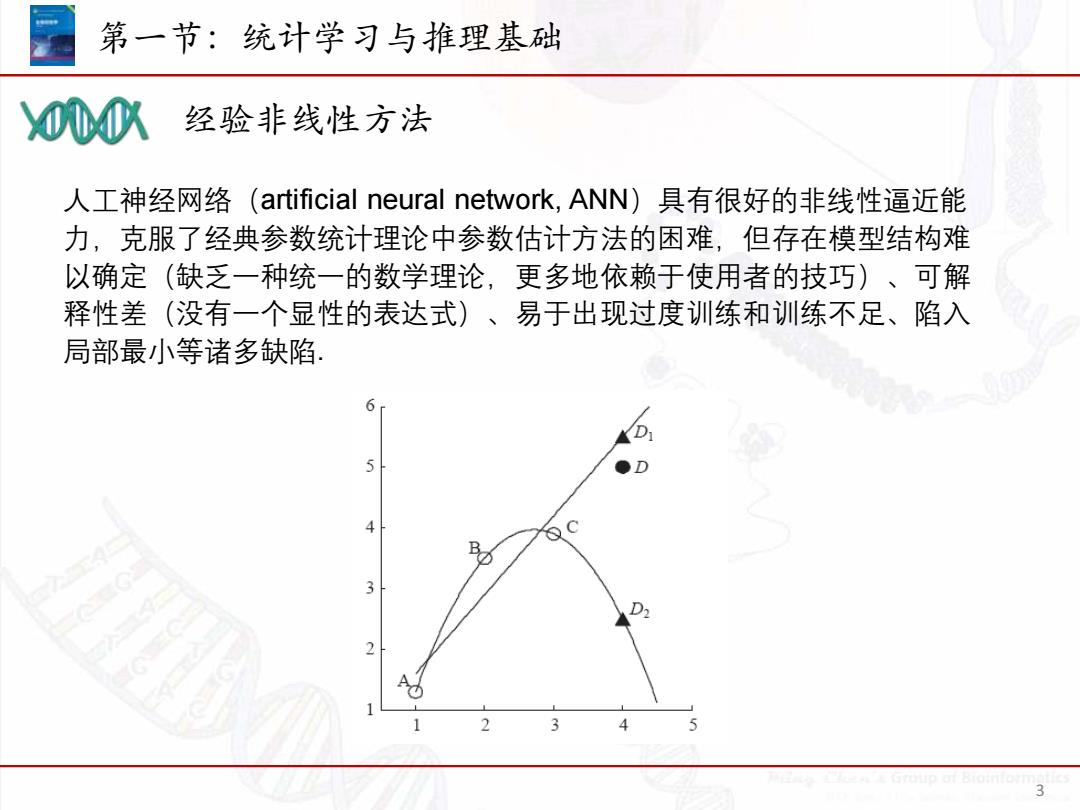
经验非线性方法 第一节:统计学习与推理基础 3 人工神经网络(artificial neural network, ANN)具有很好的非线性逼近能 力,克服了经典参数统计理论中参数估计方法的困难,但存在模型结构难 以确定(缺乏一种统一的数学理论,更多地依赖于使用者的技巧)、可解 释性差(没有一个显性的表达式)、易于出现过度训练和训练不足、陷入 局部最小等诸多缺陷

第一节:统计学习与推理基础 0似小样本统计学习理论 (-)VC维 (二)推广性的界 对各种类型的函数集,统计学习理论系统地研究了其经验风险与期望风险之间 的关系,即推广性的界。 (三)结构风险最小 (四)小样本与转导推理
小样本统计学习理论 第一节:统计学习与推理基础 4 (一)VC维 (二)推广性的界 对各种类型的函数集,统计学习理论系统地研究了其经验风险与期望风险之间 的关系,即推广性的界。 (三)结构风险最小 (四)小样本与转导推理

第一节:统计学习与推理基础 00M以 基于概率的方法 基于概率的方法主要包括贝叶斯(Bayes)推理及隐马尔可夫模型(hidden Markov model,.HMM),其中贝叶斯推理需利用来源于经验和历史资料的先 验信息。 5
基于概率的方法 第一节:统计学习与推理基础 5 基于概率的方法主要包括贝叶斯(Bayes)推理及隐马尔可夫模型(hidden Markov model,HMM),其中贝叶斯推理需利用来源于经验和历史资料的先 验信息

第二节:统计模型与参数推断 000以 参数估计量的评选标准 (一)无偏性 参数估计量的期望值与参数真值是相等的,这种性质称为无偏性。具有无 偏性的估计量称为无偏估计量。 (二)有效性 (三)相合性 (四)充分性与完备性 6
参数估计量的评选标准 第二节:统计模型与参数推断 6 (一)无偏性 参数估计量的期望值与参数真值是相等的,这种性质称为无偏性。具有无 偏性的估计量称为无偏估计量。 (二)有效性 (三)相合性 (四)充分性与完备性

第二节:统计模型与参数推断 00M0以 最小二乘估计 基本思想:保证由新估参数得到的理论值与观察值离均差的平方和值为最 小。 具体方法:为使离差平方和Q为最小,可通过求Q对待参数的偏导数,并 令其等于0,以求得参数估计量
最小二乘估计 第二节:统计模型与参数推断 7 基本思想:保证由新估参数得到的理论值与观察值离均差的平方和值为最 小。 具体方法:为使离差平方和Q为最小,可通过求Q对待参数的偏导数,并 令其等于0,以求得参数估计量

第二节:统计模型与参数推断 000八 最小二乘估计 例:用最小二乘法求总体平均数:的估计量」 若从平均数为的总体中抽得样本为1,2,,…,y,则观察值可剖分为总体平均数 u与误差e,之和,即 y=十e (12.2.1) 总体平均数:的最小二乘估计量就是使y与估计值“间的离差平方和为最小,即 -v (12.2.2) 为获得其最小值,求Q对u的导数,并令导数等于0,可得 器90w (12.2.3) 即总体平均数的估计量为 (12.2.4) 因此,算数平均数为总体平均数的最小二乘估计。 一般地,若个自变数x1,x2,x,…,xm与依变数y存在统计模型关系, y=f(x1,2,3,…,xm;01,82,…,0)十e (12.2.5) 式中,日,02,…,为待估参数。 通过n次观测(n>k)得到n组含有x,x,…,x,为(i=1,2,…,n)的数据,以 估计日1,02,…,0。其最小二乘估计值为使 0-2-2f…k:44…户 (12.2.6) 为最小的,a2,…,a。 8
最小二乘估计 第二节:统计模型与参数推断 8

第二节:统计模型与参数推断 00M以 最大似然估计 (一)似然函数 对于离散型随机变量,似然函数是多个独立事件的概率函数的乘积,该乘 积是概率函数值,它是关于总体参数的函数。 例:一只大口袋里有红、白、黑3种球,采用复置抽50次,得到红、白、 黑3种球的个数分别为12、24、14,根据多项式的理论建立似然函。 (二)最大似然估计 所谓最大似然估计就是指使似然函数值为最大以获得总体参数估计的方法。 例:求红、白、黑球实例中的最大似然估计值。 9
最大似然估计 第二节:统计模型与参数推断 9 (一)似然函数 对于离散型随机变量,似然函数是多个独立事件的概率函数的乘积,该乘 积是概率函数值,它是关于总体参数的函数。 例:一只大口袋里有红、白、黑3种球,采用复置抽50次,得到红、白、 黑3种球的个数分别为12、24、14,根据多项式的理论建立似然函。 (二)最大似然估计 所谓最大似然估计就是指使似然函数值为最大以获得总体参数估计的方法。 例:求红、白、黑球实例中 的最大似然估计值

第三节:聚类分析、主成分分析与Fisher.判别 00M八 聚类分析 (一)数据变换 1)中心化变换。 ,-,1,2,:户l2m∑/n 2)规格化变换。 号(i,(a,}一c,) 3)标准化变换。 公空到 4)对数变换。 x号lnx,x,>0 10
聚类分析 第三节:聚类分析、主成分分析与Fisher判别 10 (一)数据变换

第三节:聚类分析、主成分分析与Fisher.判别 00M 【聚类分析 (二)距离尺度函数 常用的距离度量包括几何距离、线性相关系数、非线性相关系数、互信息 等。 11
聚类分析 第三节:聚类分析、主成分分析与Fisher判别 11 (二)距离尺度函数 常用的距离度量包括几何距离、线性相关系数、非线性相关系数、互信息 等