
第一节红外吸收光谱及主要用途 红外光谱在化学领域中的应用 红外光谱在化学领域中的应用大体上可分为两个方 面:一是用于分子结构的基础研究,应用红外光谱可以 测定分子的键长、键角,以此推断出分子的立体构型; 根据所得的力常数可以知道化学键的强弱;由简正频率 来计算热力学函数。二是用于化学组成的分析,红外光 谱最广泛的应用在于对物质的化学组成进行分析,用红 外光谱法可以根据光谱中吸收峰的位置和形状来推断未 知物结构,依照特征吸收峰的强度来测定混合物中各组 分的含量,它已成为现代结构化学、分析化学最常用和 不可缺少的工具。 疮潮清商業大孕 HARBIN LNTVERSITY OP COMMERCE
红外光谱在化学领域中的应用大体上可分为两个方 面:一是用于分子结构的基础研究,应用红外光谱可以 测定分子的键长、键角,以此推断出分子的立体构型; 根据所得的力常数可以知道化学键的强弱;由简正频率 来计算热力学函数。二是用于化学组成的分析,红外光 谱最广泛的应用在于对物质的化学组成进行分析,用红 外光谱法可以根据光谱中吸收峰的位置和形状来推断未 知物结构,依照特征吸收峰的强度来测定混合物中各组 分的含量,它已成为现代结构化学、分析化学最常用和 不可缺少的工具。 一、红外光谱在化学领域中的应用 第一节 红外吸收光谱及主要用途

红外光区的划分 习惯上按红外线波长,将红外光谱分成三个区域: 近红外区:0.78~2.5μm(12820~4000cm1),主要 用于研究分子中的0一H、N一H、C一H键的振动倍频与组频。 2、中红外区:2.5~25μm(4000400cm1),主要用于研 究大部分有机化合物的振动基频。, 3、远红外区:25~300μm(400~33cm1),主要用于研究 分子的转动光谱及重原子成键的振动。 其中,中红外区(2.5~25μm即4000~400cm1)是 研究和应用最多的区域,通常说的红外光谱就是指中红外 区的红外吸收光谱。红外光谱除用波长入表征横坐标外, 更常用波数(wave number)表征。纵坐标为百分透射比T %。 宏源演商業大圣 HARBIN LNTVERSTTY OF COMMERCE
二、红外光区的划分 习惯上按红外线波长,将红外光谱分成三个区域: 1、近红外区:0.78~2.5μm(12 820~4 000cm-1),主要 用于研究分子中的O—H、N—H、C—H键的振动倍频与组频。 2、中红外区:2.5~25μm(4 000~400cm-1),主要用于研 究大部分有机化合物的振动基频。 3、远红外区:25~300μm(400~33cm-1),主要用于研究 分子的转动光谱及重原子成键的振动。 其中,中红外区(2.5~25μm即4 000~400cm-1)是 研究和应用最多的区域,通常说的红外光谱就是指中红外 区的红外吸收光谱。红外光谱除用波长λ表征横坐标外, 更常用波数(wave number)表征。纵坐标为百分透射比T %

E、 红外光谱法的特点 1、特征性高。就像人的指纹一样,每一种化合物都 有自己的特征红外光谱,所以把红外光谱分析形象 的称为物质分子的“指纹”分析。 2、应用范围广。从气体、液体到固体,从无机化合 物到有机化合物,从高分子到低分子都可用红外光 谱法进行分析。 3、用样量少,分析速度快,不破坏样品。 疮潮清月業大孕 HARBIN LNTVERSITY OP COMMERCE
三、 红外光谱法的特点 1、特征性高。就像人的指纹一样,每一种化合物都 有自己的特征红外光谱,所以把红外光谱分析形象 的称为物质分子的“指纹”分析。 2、应用范围广。从气体、液体到固体,从无机化合 物到有机化合物,从高分子到低分子都可用红外光 谱法进行分析。 3、用样量少,分析速度快,不破坏样品

第二节红外吸收光谱基本原理 二、产生红外吸收的条件 红外光谱是由于分子振动能级(同时伴随转动。 能级)跃迁而产生的,物质吸收红外辐射应满足两 ,个条件: (1)辐射光具有的能量与发生振动跃迁时所需的能 ,量相等;, (2)辐射与物质之间有偶合作用。 给潮清月掌大呈 HARBIN LNTVERSTTY OF COMMERCE
第二节 红外吸收光谱基本原理 一、 产生红外吸收的条件 红外光谱是由于分子振动能级(同时伴随转动 能级)跃迁而产生的,物质吸收红外辐射应满足两 个条件: (1)辐射光具有的能量与发生振动跃迁时所需的能 量相等; (2)辐射与物质之间有偶合作用
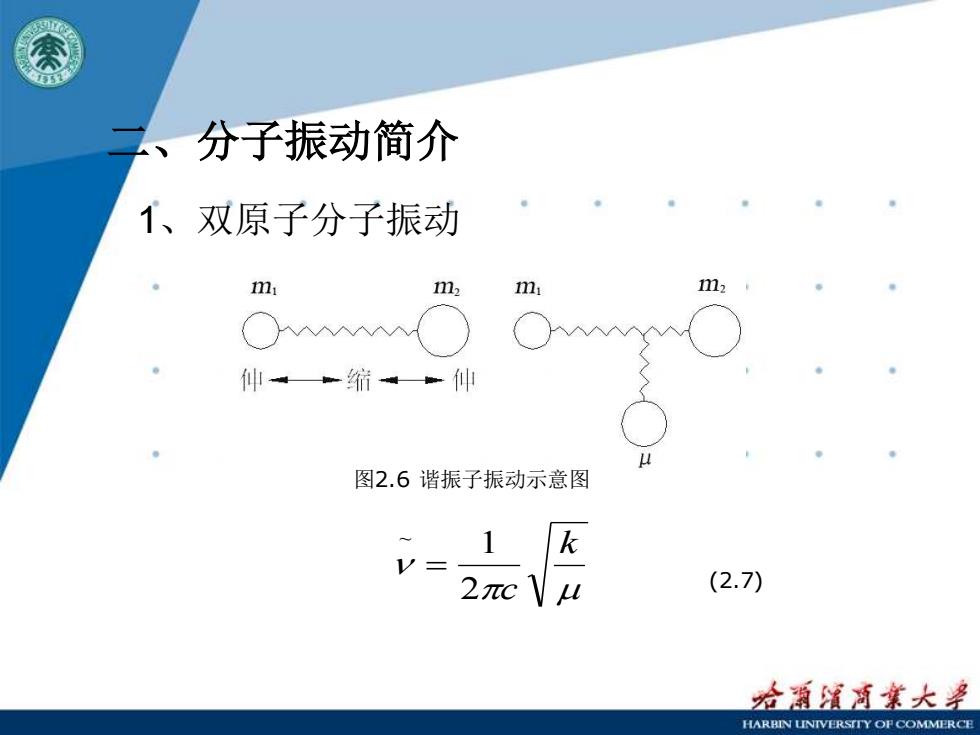
、 分子振动简介 1、双原子分子振动 m m, 1m2 仲缩。仲 图2.6谐振子振动示意图 k V= 2πc (2.7) 给源清商業大 HARBIN LNTVERSITY OF COMMERCE
二、分子振动简介 1、双原子分子振动 图2.6 谐振子振动示意图 k 2 c 1 ~ = (2.7)

武中:k是弹簧力常数,也即连接原子的化学键的力常数 (两原子由平衡位置伸长1A0的恢复力,单位为Ncm1) (2.8) (式中a,b一常数X,X,一原子电负性N一价键数 d一平衡核间距);·是两个小球(即两个原子)的折合 质量(单位为g) u≥ m1*m2 m1+m2 (2.9) 分酒爱商常大多 HARBIN LNTVERSTTY OF COMMERCE
式中:k是弹簧力常数,也即连接原子的化学键的力常数 (两原子由平衡位置伸长1A0的恢复力,单位为N·cm-1) (式中a,b—常数 xa,xb—原子电负性 N—价键数 d—平衡核间距); μ是两个小球(即两个原子)的折合 质量(单位为g) b d x x k a N a b = ( ) + 2 1 2 1 2 m m m m μ + = (2.8) (2.9)

根据小球的质量和相对原子质量之间的关系,式 (2.7)可写作: A V= 2.10 2πcVM 其中Na为阿伏加德罗(Avogadro)常数 (6.022×1023),M是折合相对原子质量,. M= M1*M2 2.11 M1+M2 疮爾清月業大孕 HARBIN LNTVERSITY OP COMMERCE
根据小球的质量和相对原子质量之间的关系,式 (2.7)可写作: 其中NA 为阿伏加德罗(Avogadro)常数 (6.022×1023),M是折合相对原子质量, M k c N v A 2 1/ 2 ~ = 1 2 1 2 M M M M M + = 2.10 2.11

式(2.10)为分子的振动方程式。由此式可见, 影响基本振动频率的直接因素是相对原子质量和化学 键的力常数。谐振子的振动频率和原子的质量有关, 而与外界能量无关,外界能量只能使振动振幅加大 (频率不变)。 对于多原子分子中的每个化学键也可以看成一个 谐振子。 给酒渭商業大是 HARBIN LNTVERSTTY OF COMMERCE
式(2.10)为分子的振动方程式。由此式可见, 影响基本振动频率的直接因素是相对原子质量和化学 键的力常数。谐振子的振动频率和原子的质量有关, 而与外界能量无关,外界能量只能使振动振幅加大 (频率不变)。 对于多原子分子中的每个化学键也可以看成一个 谐振子

2 振动的量子化处理 根据量子力学,其分子的振动能 .E=(o+1/2)hv振 (2.12) 在光谱学中,体系从能量E变到能量E,',要遵循一 定的规则,即选择定则,谐振子振动能级的选择定则 △)=±1。由选择定则可知,振动能级跃迁只能发生在 相邻的能级间。 E=o+112)2元V2 h k (2.13) 哈源頒章大孕 HARBIN LNTVERSITY OP COMMERCE
2、振动的量子化处理 根据量子力学,其分子的振动能 E=(υ+1/2)h v振 (2.12) 在光谱学中,体系从能量E变到能量E1',要遵循一 定的规则,即选择定则,谐振子振动能级的选择定则 △υ=±1。由选择定则可知,振动能级跃迁只能发生在 相邻的能级间 。 k π h E υ 2 = ( +1/ 2) (2.13)

根据选择定则:可得任一相邻能级间能量差为: AE= h 2πu (2.14) 当照射的电磁辐射能正好能使振动能级跃迁时: 给酒渭商業大是 HARBIN LNTVERSTTY OF COMMERCE
根据选择定则:可得任一相邻能级间能量差为: 当照射的电磁辐射能正好能使振动能级跃迁时: h k E 2 = (2.14)