
换院究研濟腿南曼王季大們厦餐 WI8目 Convergences and Limit Theorems Professor Yongmiao Hong Cornell University April 16,2020
Convergences and Limit Theorems Professor Yongmiao Hong Cornell University April 16, 2020

CONTENTS 7.1 Limits and Orders of Magnitude:A Review 7.2 Motivation for Convergence Concepts 7.3 Convergence in Quadratic Mean and Lp-Convergence 7.4 Convergence in Probability 7.5 Almost Sure Convergence 7.6 Convergence in Distribution 7.7 Central Limit Theorems 7.8 Conclusion Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 2/186
Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 2/186 7.1 Limits and Orders of Magnitude: A Review 7.2 Motivation for Convergence Concepts 7.3 Convergence in Quadratic Mean and 𝑳𝑳𝒑𝒑-Convergence 7.4 Convergence in Probability 7.5 Almost Sure Convergence 7.6 Convergence in Distribution 7.7 Central Limit Theorems 7.8 Conclusion CONTENTS

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Definition 1 (7.1).[Limit] Let fon,n=1,2,...}be a sequence of nonstochastic real numbers.If there exists a real number b such that for every real number e>0,there exists a finite integer N(e)such that for all nN(e),we have on-b<e,then b is the limit of the sequence fon,n 1,2,...}. 2) n 十十十十十十十十十十十 n 十 23456789101112131415 23456789101112131415 Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 3/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 3/186 Definition 1 (7.1). [Limit] Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Remarks: ◆When{bn}converges to b as n→o,we write bm→basm→o, or lim on =b. m→o∞ The constant e>0 can be set to be arbitrarily small. The smaller e is,the larger N(e)will be.One can inter- pret e as a prespecified tolerance level for the discrep- ancy between bn and b. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 4/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 4/186 Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review Remarks:

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 1 (7.1) bn=(-l)r.Then{bn,n=l,2,·…}is bounded by a constant in the sense that on1 and for all n 1.However,its limit does not exist. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 5/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 5/186 Example 1 (7.1) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review
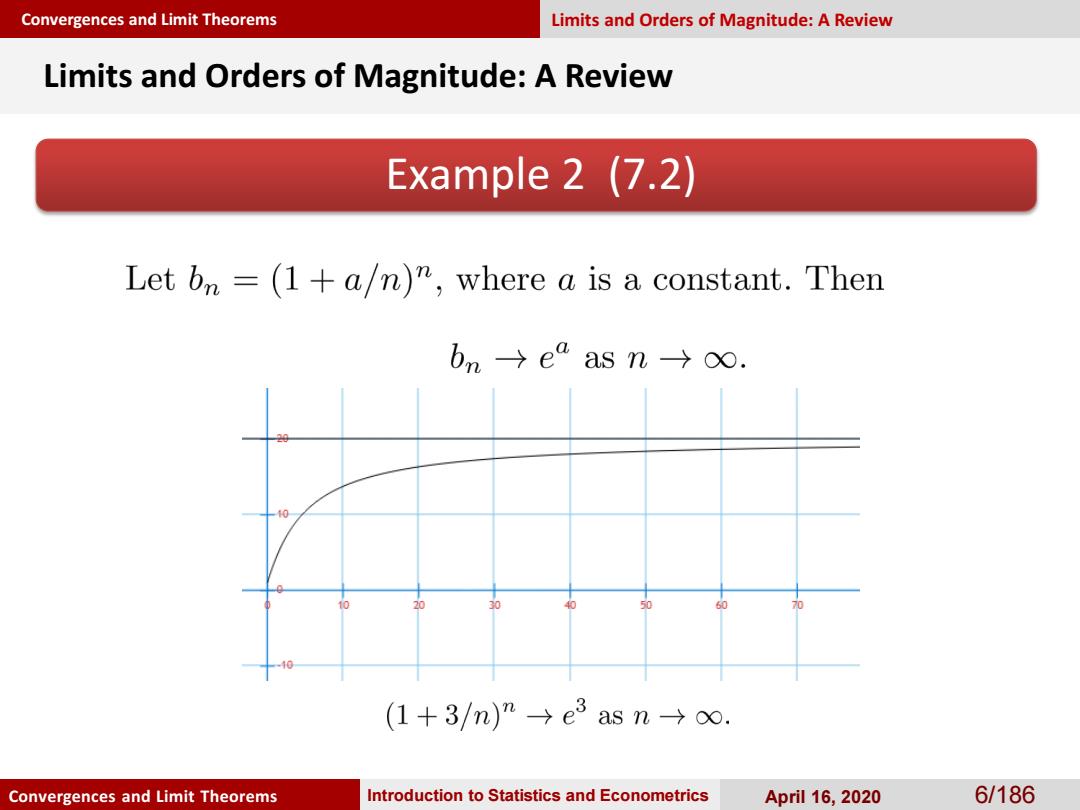
Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 2 (7.2) Let on=(1+a/n)",where a is a constant.Then bn→ea as n→o. 40 (1+3/m)n→e3asn→o. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 6/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 6/186 Example 2 (7.2) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 3 (7.3) on=(-1)".Then fon,n 1,2,...}is bounded by a constant in the sense that on1 and for all n 1.However,its limit does not exist. Solution Set e=.Then there exist no b and N(e)such that for all n >N(e),we can have bn -b<e. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 7/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 7/186 Example 3 (7.3) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review Solution

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Definition 2 (7.2).[Continuity] The function g:R->R is continuous at point b if for any sequence{bn}such that on→basn→o,we have g(bn)→g(b)asn→o. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 8/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 8/186 Definition 2 (7.2). [Continuity] Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Remarks: An alternative but equivalent definition of continuity: for each given e>0 there exists a 6=(e)such that whenever on-bl 6,we have lg(on)-g(b)<c. When g()is continuous at b,we can write im。g6n)=gibm)=g6). n→oa In other words,the limit of a sequence of values for a continuous function is equal to the value of the function at the limit. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 9/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 9/186 Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review Remarks:

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 4 (7.4) Suppose an→a and bn→basm→o.Then as n→o, (1)an+bn→a+b; (2)anbn→ab; (3)an/bn→a/bifb≠0. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 10/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 10/186 Example 4 (7.4) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review