
第一章传输线理论 ◆§1.1传输线方程及其解 ◆§1.2均匀无耗长线的工作状态 ◆§1.3圆图及阻抗匹配 ◆§1.4波导与同轴线 ◆§1.5平面传输线 2018年6月6日星期三
2018年6月6日星期三 第一章 传输线理论 §1.1 传输线方程及其解 §1.2 均匀无耗长线的工作状态 §1.3 圆图及阻抗匹配 §1.4 波导与同轴线 §1.5 平面传输线

§1.4波导与同轴线 波导与同轴线是封闭的微波传输系统。 对于波导传输线,只能用场理论分析: 对于同轴线,由于是双导体结构,线上电压电流具有 确切定义,其传输的主模式是TEM波,因此既可以用长 线理论分析,也可用场理论分析。 用电磁场理论,建立导波系统的一般理论及模式电 压和模式电流的概念,导出与长线理论中的传输线方程 相类似的广义传输线方程。这样无论是TEM波、还是非 TEM波传输线,在广义传输线理论下,其传输线方程具 有相同的形式。 ·讨论波导与同轴线的传输特性。 STE_A.J.YUE 西安电子科技大学通信工程学院 2
STE_A.J.YUE 西安电子科技大学通信工程学院 2 §1.4 波导与同轴线 波导与同轴线是封闭的微波传输系统。 对于波导传输线,只能用场理论分析; 对于同轴线,由于是双导体结构,线上电压电流具有 确切定义,其传输的主模式是 TEM 波,因此既可以用长 线理论分析,也可用场理论分析。 ·用电磁场理论,建立导波系统的一般理论及模式电 压和模式电流的概念,导出与长线理论中的传输线方程 相类似的广义传输线方程。这样无论是 TEM 波、还是非 TEM 波传输线,在广义传输线理论下,其传输线方程具 有相同的形式。 ·讨论波导与同轴线的传输特性
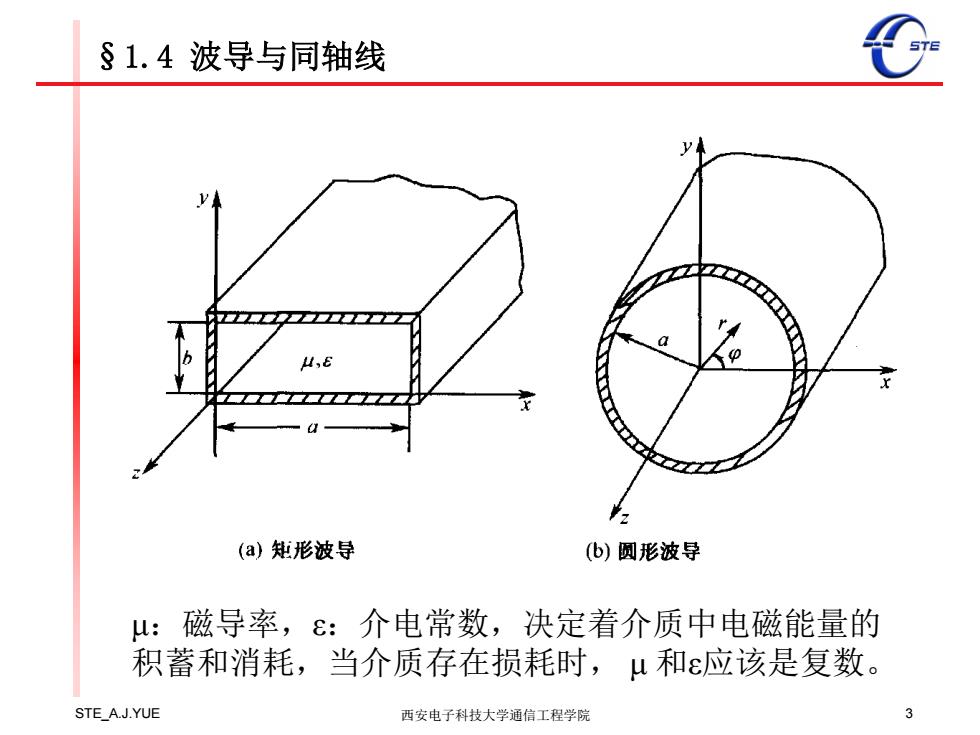
§1.4波导与同轴线 (a)矩形波导 (6)圆形波导 u: 磁导率,ε:介电常数,决定着介质中电磁能量的 积蓄和消耗,当介质存在损耗时,u和ε应该是复数。 STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 3 §1.4 波导与同轴线 μ:磁导率,ε:介电常数,决定着介质中电磁能量的 积蓄和消耗,当介质存在损耗时, μ 和ε应该是复数
§1.4波导与同轴线 =% (心)同轴线的结构 STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 4 §1.4 波导与同轴线

、 理想导波系统的一般分析 1、横、纵场分量的关系 理想导波系统中的电磁场,可以直接对麦克斯韦方程 求解,下面通过麦克斯韦方程组导出横纵向场分量间的关 系及所满足的方程。 设所研究的导波系统由无限长理想导体和各向同性的 理想介质构成,并且介质是均匀填充于系统中。对于按正 弦规律变化的电磁场,其满足无源区的麦克斯韦方程: VX H=j@EE VXE =-jw uH V。H=0 V·E=0 STE_A.J.YUE 西安电子科技大学通信工程学院 5
STE_A.J.YUE 西安电子科技大学通信工程学院 5 一、理想导波系统的一般分析 1 、横、纵场分量的关系 理想导波系统中的电磁场,可以直接对麦克斯韦方程 求解,下面通过麦克斯韦方程组导出横纵向场分量间的关 系及所满足的方程。 设所研究的导波系统由无限长理想导体和各向同性的 理想介质构成,并且介质是均匀填充于系统中。对于按正 弦规律变化的电磁场,其满足无源区的麦克斯韦方程:

用广义柱坐标系(41,42,-),其中41及2为导波系统横截面 上的坐标,z为纵向坐标。场强的纵向分量用E(4,42,2)和 H.(41,2,z)表示,场强的横向分量用E,(1,42,2)和H(u1,42,2)表 示,稀度算子为:。-可+0名 则场强矢量可写成: E(u1,u2,之)=E(u1,u2,z)十E2(u1,u2,z)=E:十Ez H(u1,u2,x)=H(u1,2,z)十H2(u1,w2,之)=H:+H2 由旋度方程可得 VX H.jwE aH 了XH.+a:X3z jweEt VX E:=-jouH aE VXE2十a:X ax =-j@uH STE A.J.YUE 四女巴丁件仪人子烟同上任子阮 6
STE_A.J.YUE 西安电子科技大学通信工程学院 6 用广义柱坐标系(u1 ,u2 ,z),其中u1及u2为导波系统横截面 上的坐标,z为纵向坐标。场强的纵向分量用 Ez (u1 ,u2 ,z)和 Hz (u1 ,u2 ,z)表示,场强的横向分量用Et (u1 ,u2 ,z)和Ht (u1 ,u2 ,z)表 示,梯度算子为: ,则场强矢量可写成: t z a z 由旋度方程可得

(k2+ 02 )E=员E:+j四a,XH. az )H=.H,-jo6a,X又E 日2 可得各场量所满足的矢量及标量亥姆霍兹方程为 V2E:+k2E:=0 72H十k2H:=0 V2E2十k2E2=0 V2H2+k2H,=0 式中k=ω√E为电磁波在无限媒质中的波数,由 分离变量法可知,E、H的解可表示成孔4,w2)e江,其中 Y=√:一称为导波的传播常数,这样横、纵场量的 关系可表示成: STE_A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 可得各场量所满足的矢量及标量亥姆霍兹方程为 式中 为电磁波在无限媒质中的波数,由 分离变量法可知,Ez、Hz的解可表示成 f(u1 ,u2 )e-gz ,其中 g 称为导波的传播常数,这样横、纵场量的 关系可表示成:

E= 1(-YVE:+jwua:X V.H.) k H:= YV.H,-jwea.XVE V2E+k2E=0 VH:十H=0 VE2十总E,=0 VH2十总H2=0 纵向解 →Ez →Hz 1 0Ez 波动方程 nidur 横向解 Eut -Y 0 0 -jω ∂Ez 1 Eu2 1 0 -Y jωu 0 n2 u2 Huk k好 0 jωe -Y 0 1∂Hz Hu2 L-jωe 0 0 -Y h1∂u1 1 OHz h2 0u2- STE_A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院

§1.4波导与同轴线 2、导行波波形的分类 导行波的波形是指能够单独在导波系统中存在的电 磁场结构形式,也叫传输模式。 导波横向场分量只与纵向场分量有关,因此可根据 导行波中是否存在纵向场分量,对导行波的波形进行分 类。 (1)横电磁波(TEM波) 此传输模式没有电磁场的纵向场量,即E,=H,=O,要 使E和H不为零,必须有k。=0即 y=Vk好-k2=jB=k TEM波的存在条件:横电磁波在导波系统横截面上的场 分布与相同条件下静止场的分布形式一样。这说明只有能 够建立静止场的导波系统,才能传输TEM波。因此TEM 波模式只能存在于多导体传输系统中。 STE_A.J.YUE 西安电子科技大学通信工程学院 9
STE_A.J.YUE 西安电子科技大学通信工程学院 9 §1.4 波导与同轴线 2、导行波波形的分类 导行波的波形是指能够单独在导波系统中存在的电 磁场结构形式,也叫传输模式。 导波横向场分量只与纵向场分量有关,因此可根据 导行波中是否存在纵向场分量,对导行波的波形进行分 类。 ( 1 )横电磁波( TEM 波) 此传输模式没有电磁场的纵向场量,即 Ez=Hz =0,要 使 Et和 Ht不为零,必须有 kc =0即 2 2 c g k k j jk TEM 波的存在条件:横电磁波在导波系统横截面上的场 分布与相同条件下静止场的分布形式一样。这说明只有能 够建立静止场的导波系统,才能传输 TEM 波。因此 TEM 波模式只能存在于多导体传输系统中

§1.4波导与同轴线 (2)横电波(TE波)或磁波(H波) 此波形的特征是E,=O,H0,所有的场分量可由纵向 磁场分量H求出。 (3)横磁波(TM波)或电波(E波) 此波形的特征是E,0,H,=0,所有的场分量可由纵向 电场分量E,求出。 在某些特殊的场合,单独用TE波或TM波不能满足 所有的边界条件,但它们的线性组合总能满足这些特殊要 求,并且提供一个完整而普遍的解,这时的波称为混合波。 当然还有别的分类方法,但按上述方法分类的三种波形是 最实用的。 STE A.J.YUE 西安电子科技大学通信工程学院 10
STE_A.J.YUE 西安电子科技大学通信工程学院 10 §1.4 波导与同轴线 (2)横电波(TE波)或磁波( H 波) 此波形的特征是Ez =0,Hz≠0,所有的场分量可由纵向 磁场分量Hz求出。 (3)横磁波(TM波)或电波(E波) 此波形的特征是Ez≠0,Hz =0,所有的场分量可由纵向 电场分量 Ez求出。 在某些特殊的场合,单独用 TE 波或 TM 波不能满足 所有的边界条件,但它们的线性组合总能满足这些特殊要 求,并且提供一个完整而普遍的解,这时的波称为混合波。 当然还有别的分类方法,但按上述方法分类的三种波形是 最实用的