
第一章传输线理论 ◆§1.1传输线方程及其解 ◆§1.2均匀无耗长线的工作状态 ◆§1.3圆图及阻抗匹配 ◆§1.4波导与同轴线 ◆§1.5平面传输线 2018年6月6日星期三
2018年6月6日星期三 第一章 传输线理论 §1.1 传输线方程及其解 §1.2 均匀无耗长线的工作状态 §1.3 圆图及阻抗匹配 §1.4 波导与同轴线 §1.5 平面传输线

§1.3圆图及阻抗匹配 从前面的讨论可以看出,分析长线的工作状态离不开 计算阻抗、反射系数等参数,会遇到大量繁琐的复数运算。 为了简化运算,图解法是常用的手段之一。在天线和微波 工程设计中,经常会用到各种图形曲线,它们既简便直观, 又具有足够的准确度,对天线和微波工程设计有着重要的 影响作用。下面介绍阻抗圆图,也称Smith圆图。 一、圆图的构成 在传输线的输入阻抗与反射系数一节中,已知均匀无 耗传输线上某点的反射系数与终端负载反射系数及某点的 等效输入阻抗之间有下述关系 (1-13 T()=「m+r,=「e2 Zm()=Z-) 1+T(z) F.-Z-2-IL.lem Z.Zo T(z)= Zn(=)-Zo T(2)=Ie(o-20-) Zn(=)+Zo STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 2 §1.3 圆图及阻抗匹配 从前面的讨论可以看出,分析长线的工作状态离不开 计算阻抗、反射系数等参数,会遇到大量繁琐的复数运算。 为了简化运算,图解法是常用的手段之一。在天线和微波 工程设计中,经常会用到各种图形曲线,它们既简便直观, 又具有足够的准确度,对天线和微波工程设计有着重要的 影响作用。下面介绍阻抗圆图,也称Smith圆图。 一、圆图的构成 在传输线的输入阻抗与反射系数一节中,已知均匀无 耗传输线上某点的反射系数与终端负载反射系数及某点的 等效输入阻抗之间有下述关系 2 L 0 L L 0 ( ) L j z u v L j L z j e Z Z e Z Z 0 0 0 1 ( ) ( ) 1 ( ) ( ) ( ) ( ) in in in z Z z Z z Z z Z z Z z Z ( 2 ) ( ) L j z L z e (1-13f)

§1.3圆图及阻抗匹配 阻抗千变万化,极难统一表述,因此引入归一化阻抗的 概念,用Z。归一化,统一起来作为一种情况加以研究。 归一化输入阻抗和负载阻抗定义为: Zn(=乙(-1+Ie Z-1+ Z。1-(z) Z。1-, 归一化阻抗是一个无量纲量,因此也称为标称阻抗。同时: r()= 2-l=r.+r,=「e Zin(=)+1 T(=)=Te-) 根据上述关系式在极坐标系中绘制的曲线图称为极坐 标阻抗圆图,也称其为史密斯(Smith)圆图。 STE_A.J.YUE 西安电子科技大学通信工程学院 3
STE_A.J.YUE 西安电子科技大学通信工程学院 3 §1.3 圆图及阻抗匹配 阻抗千变万化,极难统一表述,因此引入归一化阻抗的 概念,用Z0归一化,统一起来作为一种情况加以研究。 归一化输入阻抗和负载阻抗定义为: 0 0 ( ) 1 ( ) 1 ( ) 1 ( ) 1 in L L in L L Z z z Z Z z Z Z z Z , 归一化阻抗是一个无量纲量,因此也称为标称阻抗。同时: 2 L L L ( ) 1 ( ) ( ) 1 1 1 L in j z u v in L j L Z z z j e Z z Z e Z ( 2 ) ( ) L j z L z e 根据上述关系式在极坐标系中绘制的曲线图称为极坐 标阻抗圆图,也称其为史密斯( Smith )圆图

1、等反射系数圆 均匀无耗长线的特性阻抗为Z,终端接负载阻抗Z,「 为终端电压反射系数,传输线上任一点z的反射系数为: r(e=re=「m+r,F=2+r2 -arctan-2.=cos 上式表明,在「=「T,复平面上等反射系数模的轨迹 是以坐标原点为圆心、厂为半径的圆。不同的反射系数模, 就对应不同大小的圆。 因为T≤1,因此所有的反射系数圆都位于单位圆内。 这一组圆族称为等反射系数圆族。 又因为反射系数模和驻波系数有一一对应的关系,故 又称它为等驻波系数圆族。 半径为零,即坐标原点为匹配点;半径为1,表示最外 面的单位圆为全反射圆。 STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 4 1、等反射系数圆 均匀无耗长线的特性阻抗为Z0,终端接负载阻抗 ZL,L 为终端电压反射系数,传输线上任一点z'的反射系数为: 2 2 2 ( ) arctan 2 cos sin u v u v v L u v u z e j z 上式表明,在Γ=Γu +jΓv复平面上等反射系数模的轨迹 是以坐标原点为圆心、|Γ|为半径的圆。不同的反射系数模, 就对应不同大小的圆。 因为|Γ|≤1,因此所有的反射系数圆都位于单位圆内。 这一组圆族称为等反射系数圆族。 又因为反射系数模和驻波系数有一一对应的关系,故 又称它为等驻波系数圆族。 半径为零,即坐标原点为匹配点;半径为1,表示最外 面的单位圆为全反射圆
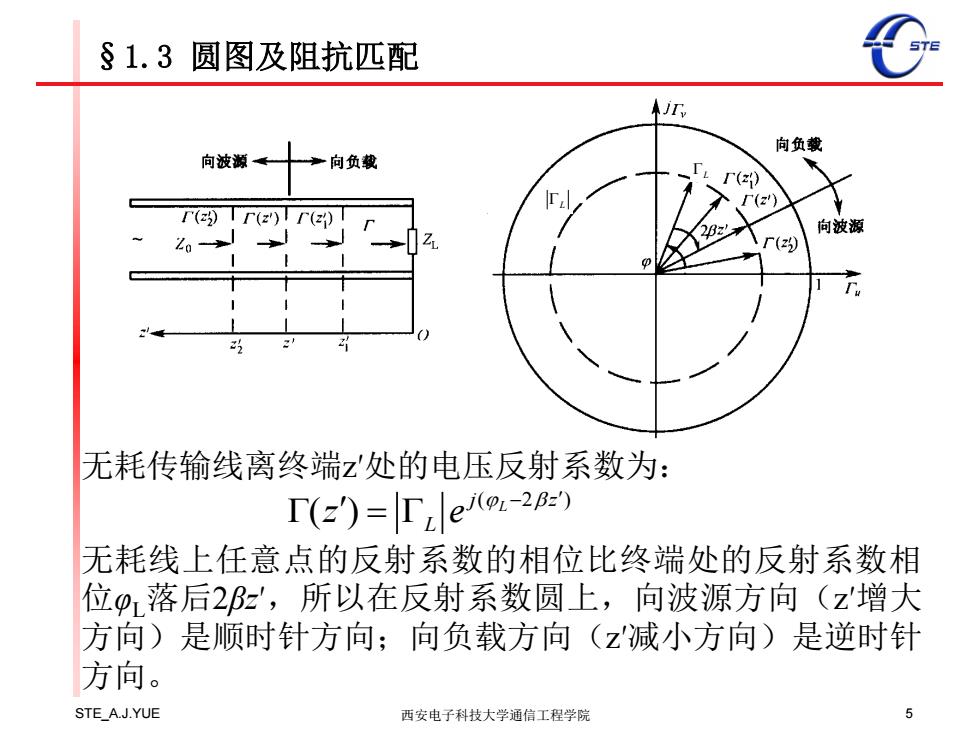
§1.3圆图及阻抗匹配 向负载 向波源← 。向负载 r() (T(z')TT(z) 向波源 201 () 无耗传输线离终端z处的电压反射系数为: T(z)=|reo-2e 无耗线上任意点的反射系数的相位比终端处的反射系数相 位p落后2Bz',所以在反射系数圆上,向波源方向(z'增大 方向)是顺时针方向;向负载方向(z减小方向)是逆时针 方向。 STE_A.J.YUE 西安电子科技大学通信工程学院 5
STE_A.J.YUE 西安电子科技大学通信工程学院 5 §1.3 圆图及阻抗匹配 无耗传输线离终端z′处的电压反射系数为: ( 2 ) ( ) L j z L z e 无耗线上任意点的反射系数的相位比终端处的反射系数相 位φL落后2βz′ ,所以在反射系数圆上,向波源方向(z′增大 方向)是顺时针方向;向负载方向(z′减小方向)是逆时针 方向。 L L

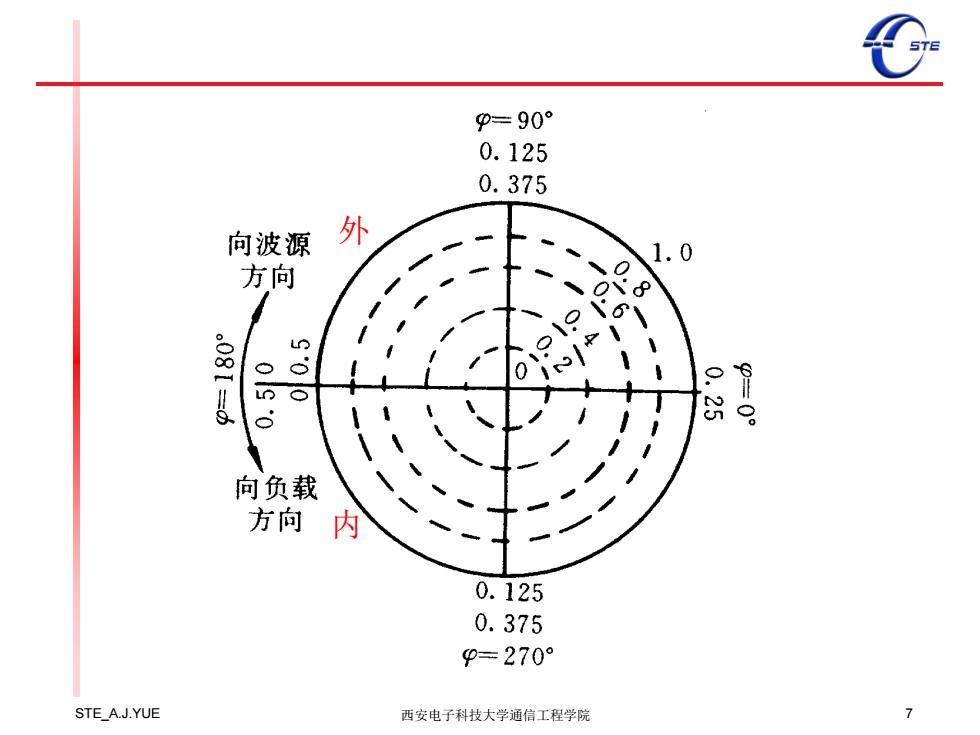
§1.3圆图及阻抗匹配 传输线上移动距离与圆图上转动角度的关系为: △p=2p=47A'=4z仁=42 △z 式中△z=△z'/元为电长度增量,当△z=0.5时,则△p =360°,1°对应的电长度是1/720,这样就可以用电长 度的改变量来描述反射系数幅角的变化。 电长度的零点可选在反射系数单位圆周上的任意位 置,但由于Z=R+X=0时,对应的反射系数为-1,位于 T=1圆的(-1,0)点,即单位圆上的π点,在该点上 恒有K=O。为使图上的所有物理零点一致,故选电长度的 零点位于(-1,0)处。 将标有角度及电长度的单位圆与复平面上的反射系 数圆族相叠加,就得到了反射系数圆。为了使用方便, 有的图上标有两个方向的电长度值,如图所示,向波源 方向移动读外圈的值,向负载方向移动读里圈的值。 STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 6 §1.3 圆图及阻抗匹配 式中 为电长度增量,当 时,则Δ =360° ,1°对应的电长度是 1 / 720,这样就可以用电长 度的改变量来描述反射系数幅角的变化。 电长度的零点可选在反射系数单位圆周上的任意位 置,但由于ZL=R+jX=0时,对应的反射系数为-1 ,位于 ||=1圆的(-1,0 )点,即单位圆上的=p点,在该点上 恒有K=0。为使图上的所有物理零点一致,故选电长度的 零点位于(-1,0)处。 将标有角度及电长度的单位圆与复平面上的反射系 数圆族相叠加,就得到了反射系数圆。为了使用方便, 有的图上标有两个方向的电长度值,如图所示,向波源 方向移动读外圈的值,向负载方向移动读里圈的值。 4 2 4 4 z z z z p p p 传输线上移动距离与圆图上转动角度的关系为: z z / z 0.5
p=90° 0.125 0.375 向波源 外 1.0 方向 0 & 8 向负载 方向 内 0.125 0.375 p=270° STE_A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 7 外 内

§1.3圆图及阻抗匹配 反射系数圆的特点: ①一个负载阻抗对应一个「,由厂确定一反射系数 圆。该圆上不同的点代表传输线上不同位置的反射系数。 ②反射系数具有入/2的重复性。电长度的零点选在 物理零点(-1,0),即π处,电长度增大的方向,也是 向波源方向,是顺时针方向旋转。 ③不同的工作状态对应的反射系数位于反射系数圆 的不同区域,匹配工作时反射系数对应单位圆圆心;驻波 工作时反射系数对应单位圆周;行驻波工作时反射系数模 值在(0,1)之间。其中右半实轴上的点(0,0<C<1) 对应是纯电阻负载或电压波腹点输入阻抗反射系数的轨迹, 左半实轴上的点(元,0<T<1)对应是纯电阻或波节 点输入阻抗反射系数的轨迹。 STE_A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 8 §1.3 圆图及阻抗匹配 反射系数圆的特点: ① 一个负载阻抗对应一个L,由|L |确定一反射系数 圆。该圆上不同的点代表传输线上不同位置的反射系数。 ② 反射系数具有/2的重复性。电长度的零点选在 物理零点(-1 , 0),即=p处,电长度增大的方向,也是 向波源方向,是顺时针方向旋转。 ③ 不同的工作状态对应的反射系数位于反射系数圆 的不同区域,匹配工作时反射系数对应单位圆圆心;驻波 工作时反射系数对应单位圆周;行驻波工作时反射系数模 值在(0,1)之间。其中右半实轴上的点(=0, 0<|L |<1) 对应是纯电阻负载或电压波腹点输入阻抗反射系数的轨迹, 左半实轴上的点( =p, 0<|L |<1 )对应是纯电阻或波节 点输入阻抗反射系数的轨迹

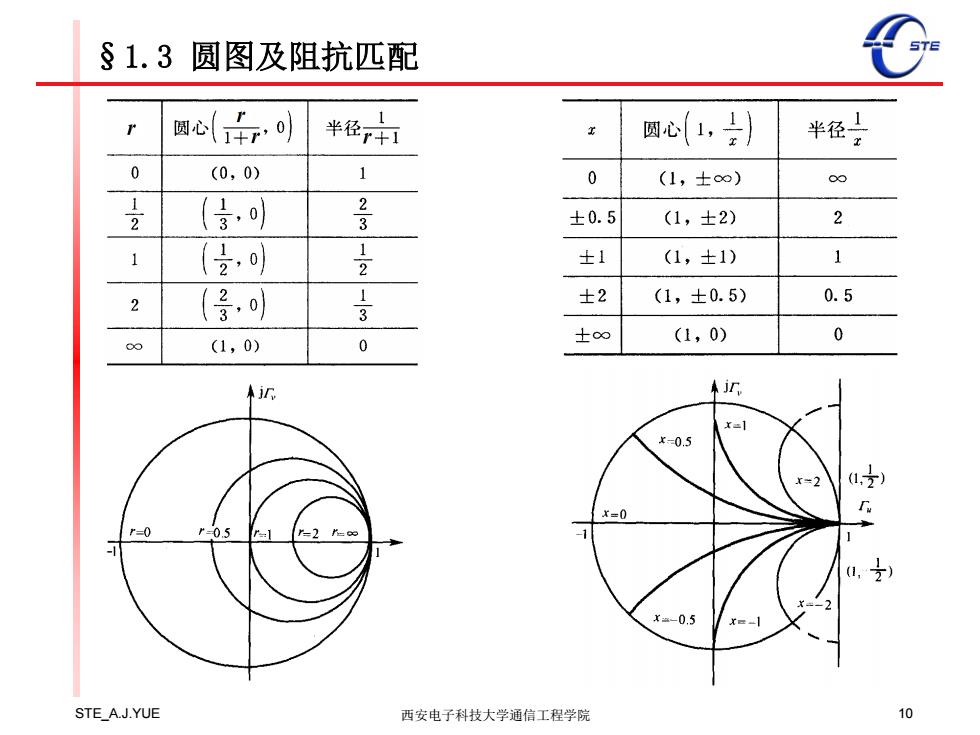
§1.3圆图及阻抗匹配 2、阻抗圆图 由Z(z) 1+), (z)=「m+汇,可得: 1-T(z) 乙(西=+r.+L-1-(+r +J 2T 1-『m-r,(1-)2+2(1-Γ)2+Γ2 =r+ix 令实部和虚部分别相等并整理化简,得到两个方程 本+r=产 ①。-2+(,-2=( 这就是Γ平面上等电阻r圆和等电抗x圆的方程。 STE_A.J.YUE 西安电子科技大学通信工程学院 9
STE_A.J.YUE 西安电子科技大学通信工程学院 9 §1.3 圆图及阻抗匹配 2、阻抗圆图 1 ( ) ( ) ( ) 1 ( ) in u v z Z z z j z 由 , 可得: 2 2 2 2 2 2 1 1 ( ) 2 ( ) 1 (1 ) (1 ) u v u v u in u v u v u v j Z z j j r jx 令实部和虚部分别相等并整理化简,得到两个方程 2 2 2 2 2 2 1 ( ) ( ) 1 1 1 1 ( 1) ( ) ( ) u v u v r r r x x 这就是平面上等电阻 r 圆和等电抗 x 圆的方程
§1.3圆图及阻抗匹配 圆心(+) 半径中 圆心(1,】 半径: 0 (0,0) 1 0 (1,土∞) 0∞ 2 (3, 号 ±0.5 (1,士2) 2 1 (,0 1 土1 (1,±1) 1 (号,0 士2 (1,±0.5) 0.5 3 (1,0) 0 士∞ (1,0) 0 x-0.5 a) r-0 -0.5 x-05 STE A.J.YUE 西安电子科技大学通信工程学院 10
STE_A.J.YUE 西安电子科技大学通信工程学院 10 §1.3 圆图及阻抗匹配