西安电子科技大学：《微波技术与天线》课程教学资源（课件讲稿）第一章 传输线理论（8/9）

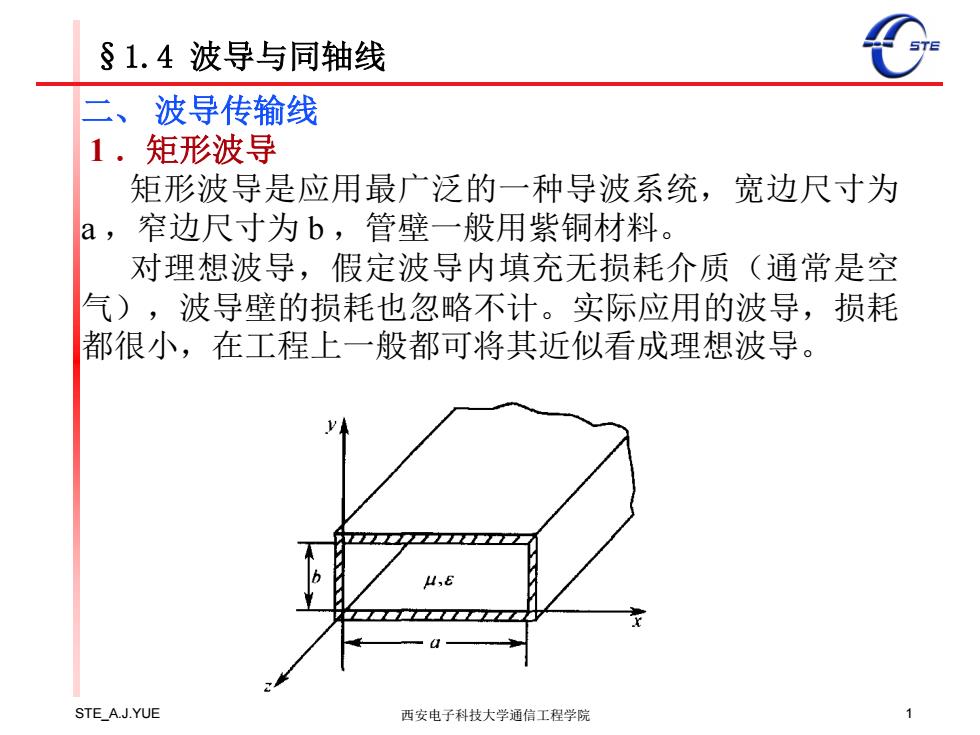
§1.4波导与同轴线 二、 波导传输线 1.矩形波导 矩形波导是应用最广泛的一种导波系统，宽边尺寸为 a,窄边尺寸为b,管壁一般用紫铜材料。 对理想波导，假定波导内填充无损耗介质（通常是空 气)，波导壁的损耗也忽略不计。实际应用的波导，损耗 都很小，在工程上一般都可将其近似看成理想波导。 STE A.J.YUE 西安电子科技大学通信工程学院

STE_A.J.YUE 西安电子科技大学通信工程学院 1 §1.4 波导与同轴线 二、 波导传输线 1 ．矩形波导 矩形波导是应用最广泛的一种导波系统，宽边尺寸为 a ，窄边尺寸为 b ，管壁一般用紫铜材料。 对理想波导，假定波导内填充无损耗介质（通常是空 气），波导壁的损耗也忽略不计。实际应用的波导，损耗 都很小，在工程上一般都可将其近似看成理想波导

§1.4波导与同轴线 STE_A.J.YUE 西安电子科技大学通信工程学院 2

STE_A.J.YUE 西安电子科技大学通信工程学院 2 §1.4 波导与同轴线

§1.4波导与同轴线 由(1-27d)可知：VE.+k2E=0V2H.+k2H.=0 其中： E.=E.(x,y)e r H.=H.(x,y)e 可得： E.(x.y)E.(x.y)+k2E.(x.y)=0 0x2 02 H.(x.y)H.(x.y)H.(x.y)=0 Ox2 0y2 分离变量，E(xy)和H(xy)都可以表示为X☒Yy) 纵向分量解为： E.(x,y)=(4 cosk x+4 sink x)(A cosk,y+4 sink,y) H.(x,y)=(B cosk,x+B2 sin k,x)(B:cosk,y+B sink,y) 其中的Ak、Bk、kx、ky为积分常数。 STE_A.J.YUE 西安电子科技大学通信工程学院 3

STE_A.J.YUE 西安电子科技大学通信工程学院 3 §1.4 波导与同轴线 由(1-27d)可知： 2 2 2 2 0 0       t z c z t z c z E k E H k H 其中： (x, y)e (x, y)e z z E E H H z z z z       可得： 2 2 2 2 2 2 2 2 2 2 (x, y) (x, y) (x, y) 0 (x, y) (x, y) (x, y) 0 z z c z z z c z E E k E x y H H k H x y               分离变量， E z (x, y) 和 H z (x, y) 都可以表示为 X(x)Y(y) 1 2 3 4 1 2 3 4 (x, y) ( cos sin )( cos sin y) (x, y) ( cos sin )( cos sin y) z x x y y z x x y y E A k x A k x A k y A k H B k x B k x B k y B k       纵向分量解为： 其中的Ak、Bk、kx、ky为积分常数

§1.4波导与同轴线 (1)TM波 TM波E.≠0H.=0而且 E.=(A cosk x+sink x)(A cosk,y+4 sink,y)e 代入TM波的边界条件： 横向电场为零，波导内壁表面电 场切向分量为零。 E:l-0=E:l-0=E:ly-0=E:ly=0 得到：A=04=0飞，=mz k,= b 即： 将上式及y=jB代入式(1-28)即可得到TM波的各 个场分量 STE A.J.YUE 西安电子科技大学通信工程学院

STE_A.J.YUE 西安电子科技大学通信工程学院 4 §1.4 波导与同轴线 ( 1 ) TM 波 代入TM 波的边界条件： TM 波 0 0 E H z z   而且 1 2 3 4 ( cos sin )( cos sin y)e z E A k x A k x A k y A k z x x y y     0 0 | | | | 0 E E E E z x z x a z y z y b         横向电场为零，波导内壁表面电 场切向分量为零。 1 3 0 0 x y m n A A k k a b   得到：     2 2 2 2 2 c x y m n k k k a b                   即： 0 sin sin e z z m n E E x y a b                 将上式及 代入式（1-28）即可得到TM波的各 个场分量    j

§1.4波导与同轴线 TM波各场分量的完整解为： .=-jg是os-sn(e E,=-j是m产（学） E.-Esin()sin e H.E,sin )cos) H,=-iao(g-sin(爱)e* STE_A.J.YUE 西安电子科技大学通信工程学院 5

STE_A.J.YUE 西安电子科技大学通信工程学院 5 §1.4 波导与同轴线 TM 波各场分量的完整解为： 0 E z 

§1.4波导与同轴线 式中E,是振幅常数，m和n是由波导边界条件决定的 正整数，称为波指数。 m表示沿波导宽边a分布的半驻波数， n表示沿窄边b分布的半驻波数。 每一对(m，n)对应一种电磁场分布，即某种波形 (或模式)。 从E的表达式可以看出m、n不能为零，m，n的取值 只能是1,2,3，，所以矩形波导中不存在TMo、 TMmo、TMn波形，TM1是TM波中的最简单波形。为了 满足边界条件，截止波数只能取离散值。 STE_A.J.YUE 西安电子科技大学通信工程学院 6

STE_A.J.YUE 西安电子科技大学通信工程学院 6 §1.4 波导与同轴线 式中 E0是振幅常数， m 和 n 是由波导边界条件决定的 正整数，称为波指数。 m 表示沿波导宽边 a 分布的半驻波数， n 表示沿窄边 b 分布的半驻波数。 每一对（ m , n ）对应一种电磁场分布，即某种波形 （或模式）。 从Ez的表达式可以看出 m、n 不能为零，m , n的取值 只能是l，2，3，…，所以矩形波导中不存在 TM00、 TMm0、TM0n波形，TM11是TM波中的最简单波形。为了 满足边界条件，截止波数只能取离散值

§1.4波导与同轴线 (2)TE波 TE波 E.=0H.≠0 而且 H.(x,y)=(B coskx+B,sink x)(B cosk,y+Ba sink y) 代入TE波的边界条件： 横向电场为零，波导内壁表面电 场切向分量为零。 Ey ly=0=Ey l-o=E:ly-0=Exly=0 得到：B,=0B,=0飞，=m nπ = a b 即： 及=+的 mπ nπ b mπ nπ H.=Ho cos cos b 将上式及y=B代入式(1-28)即可得到TE波的各 个场分量 STE_A.J.YUE 西安电子科技大学通信工程学院

STE_A.J.YUE 西安电子科技大学通信工程学院 7 §1.4 波导与同轴线 ( 2 ) TE 波 代入TE 波的边界条件： TE 波 0 0 E H z z   而且 1 2 3 4 (x, y) ( cos sin )( cos sin y) H B k x B k x B k y B k z x x y y    0 0 | | | | 0 E E E E y x y x a x y x y b         横向电场为零，波导内壁表面电 场切向分量为零。 2 4 0 0 x y m n B B k k a b   得到：     2 2 2 2 2 c x y m n k k k a b                   即： 0 cos cos e z z m n H H x y a b                 将上式及 代入式（1-28）即可得到TE波的各 个场分量    j

§1.4波导与同轴线 (2)TE波 TE波各场分量的完整解为 E.=j器gH,os(）in()e E,=jgH,sin(小cos(e ,=j是Hnj()e H,=j是gH,cos(2x)sn(e H.-H.cos )coa) STE_A.J.YUE 西安电子科技大学通信工程学院

STE_A.J.YUE 西安电子科技大学通信工程学院 8 §1.4 波导与同轴线 ( 2 ) TE 波 TE 波各场分量的完整解为

§1.4波导与同轴线 式中H是振幅常数。 从H,的表达式可以看出m,n不能同时为零，其取值 为m=0,1,2,.;n=0,1,2,.所以矩形波导中， 不存在TE0波形。若a>b,则最简单的TE波是TE10波， 其截止波数k的表达式与TM波相同。 问题：在矩形波导的波形中，为什么没有讨论TEM波？ (3)传输特性 将所求得的TM和TE波场线性叠加，可以完整地 表示出矩形波导中所有可能存在的场。波指数m、n不 同，就有不同的场分布，而且一般也具有不同的传输 特性，但是它们都满足矩形波导的边界条件而独立地 存在于矩形波导中，这称为正规波的正交性。 STE_A.J.YUE 西安电子科技大学通信工程学院 9

STE_A.J.YUE 西安电子科技大学通信工程学院 9 §1.4 波导与同轴线 式中 H0是振幅常数。 从 Hz的表达式可以看出 m , n 不能同时为零，其取值 为 m = 0，1，2，… ； n=0，1，2，… 所以矩形波导中， 不存在 TE00波形。若 a > b ，则最简单的 TE波是 TE10波， 其截止波数 kc的表达式与 TM波相同。 （3）传输特性 将所求得的 TM 和 TE 波场线性叠加，可以完整地 表示出矩形波导中所有可能存在的场。波指数 m、n 不 同，就有不同的场分布，而且一般也具有不同的传输 特性，但是它们都满足矩形波导的边界条件而独立地 存在于矩形波导中，这称为正规波的正交性。 问题：在矩形波导的波形中，为什么没有讨论TEM波？

§1.4波导与同轴线 截止波长是决定波的传输特性的重要参数 2π 2 ke 它表明每个以波指数m、n表征的正规波，都有对应 的截止波长，而该波的传输条件为入，<入。，因此，不同的 波形有不同的传输条件。 对波指数相同的TE和TM波来说，具有相同的截止 波长，也就具有了相同的传输条件，但它们的场结构显然 是不同的。这种具有不同的场结构，而有相同的传输参数 的现象，称为“简并”。 只有TEm和TE波没有简并模，这是因为不存在 TMmo和TMn波形的缘故。 STE_A.J.YUE 西安电子科技大学通信工程学院 10

STE_A.J.YUE 西安电子科技大学通信工程学院 10 §1.4 波导与同轴线 截止波长是决定波的传输特性的重要参数 它表明每个以波指数 m 、 n 表征的正规波，都有对应 的截止波长，而该波的传输条件为l0＜lc，因此，不同的 波形有不同的传输条件。 对波指数相同的 TE 和 TM 波来说，具有相同的截止 波长，也就具有了相同的传输条件，但它们的场结构显然 是不同的。这种具有不同的场结构，而有相同的传输参数 的现象，称为“简并” 。 只有TEm0和TE0n波没有简并模，这是因为不存在 TMm0和 TM0n波形的缘故。 2 2 2 2 c c k m n a b  l               