
上游气通大学 SHANGHAI JIAO TONG UNIVERSITY 第八章 机械振动的测试 1日日6
第八章 机械振动的测试

上泽文通大学 SHANGHAI JIAO TONG UNIVERSITY 第一节机械振动的概念 1、机械振动定义 物体在一定位置附近所做的周期性往复运动。 2、机械振动产生的物理原因 机械在运动时,由于旋转件的不平衡、负载的不均匀、间隙、润滑 不良、支撑松动等因素,产生各种振动。 3、振动测试的研究内容 口测量设备运行时的振动参量,了解被测对象的振动状态,寻找 振源; 口对设备激振,测试其受迫振动,以求得被测对象的动态性能, 如固有频率、阻尼、机械阻抗等
1、机械振动定义 物体在一定位置附近所做的周期性往复运动。 2、机械振动产生的物理原因 机械在运动时,由于旋转件的不平衡、负载的不均匀、间隙、润滑 不良、支撑松动等因素,产生各种振动。 3、振动测试的研究内容 测量设备运行时的振动参量,了解被测对象的振动状态,寻找 振源; 对设备激振,测试其受迫振动,以求得被测对象的动态性能, 如固有频率、阻尼、机械阻抗等。 第一节 机械振动的概念
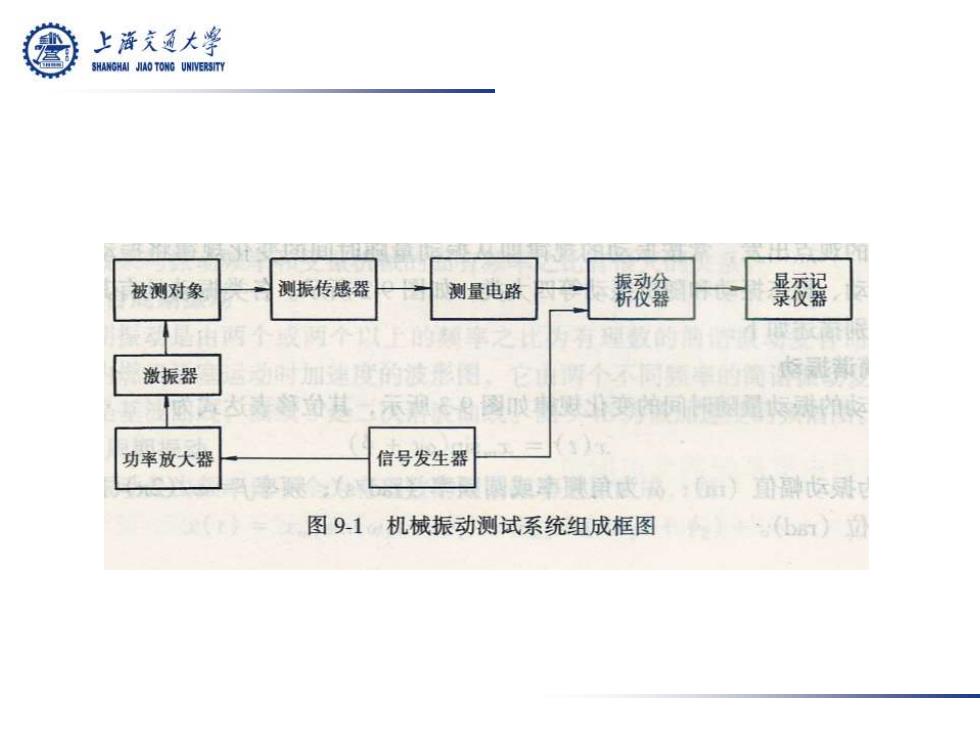
上海充通大学 SHANGHAI JIAO TONG UNIVERSITY 被测对象 测振传感器 测量电路 养被鑫 景委露 激振器 等始其,示®倒拟 功率放大器 信号发生器 题南谜食皮品,)融标鼎 图91机械振动测试系统组成框图 (6)道

上泽充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 2.1振动的分类 (1)从产生振动的方式来分: 自由振动:仅受初始条件(初始位移、初始速度) 激励而引起的振动: 受迫振动:系统在持续外力激励下的振动
2.1 振动的分类 (1)从产生振动的方式来分: 自由振动:仅受初始条件(初始位移、初始速度) 激励而引起的振动; 受迫振动:系统在持续外力激励下的振动。 第二节 机械振动的类型

上海充通大学 第二节机械振动的类型 SHANGHAI JIAO TONG UNIVERSITY (2)从振动的规律来分: ☑ 简谐振动 ☑复合周期振动 ☑ 瞬态振动 ☑ 随机振动
(2)从振动的规律来分: 简谐振动 复合周期振动 瞬态振动 随机振动 第二节 机械振动的类型

上泽文通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 简谐振动 以无阻尼自由振动的弹簧振子为例得出普遍结论: 由 F=ma=-kx 运动学特征 k 0 Q=- X=-0X m d'x 2 dt2 +x=0
以无阻尼自由振动的弹簧振子为例得出普遍结论: x o k 微分方程特征 运动学特征 由 F ma kx = = −x 0 dt d x 2 2 2 + = x x m k a 2 = − = − m k = (一) 简谐振动 第二节 机械振动的类型

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 d2x 解 dt2 +02x=0 可得 位移 x-Acos(ot+p) 振动方程 速度 v=i =-osin(ot+)=A@cos(+ π dt 加速度 i a=. dy =-Ao2 cos(ot+p)=Ao'cos() dt
加速度 2 2 cos( ) cos( ) dv a A t A t dt = = − + = + + 速 度 sin( ) cos( ) 2 dx v A t A t dt = = − + = + + 2 4 6 8 10 12 14 -1 -0.5 0.5 1 v t x a 解 可得 2 2 2 d x +ω x = 0 dt 位 移 x = Acos( t + ) 振动方程 第二节 机械振动的类型

常数A和φ的确定 x=Acos(ot+) dx V= =-@Asin(ot+p) dt 由初始条件: xo=Acoso Vo=-A@sino 说明: ()一般来说φ的取值 在-π和π(或0和2)之 tgo=- Vo 间; @xo
常数A和 的确定 0 0 2 2 0 0 x v tg v A x = − = + sin cos 0 0 v A x A = − = cos( ) sin( t ) x A t dx v A dt = + = = − + 说明: (1) 一般来说 的取值 在-π和π(或0和2π)之 间; 由初始条件:

上海充通大学 SHANGHAI JIAO TONG UNIVERSITY 结论: (1)单自由度无阻尼系统的自由振动是以正弦或余弦函数表示 的,故称为简谐振动。 (2)自由振动的角频率即系统的固有频率仅由系统本身参数确 定,与外界激励、初始条件无关。 m (3)自由振动的振幅A和初相角中由初始条件所确定
结论: (1)单自由度无阻尼系统的自由振动是以正弦或余弦函数表示 的,故称为简谐振动。 (2)自由振动的角频率即系统的固有频率仅由系统本身参数确 定,与外界激励、初始条件无关。 (3)自由振动的振幅A和初相角φ由初始条件所确定。 k m =
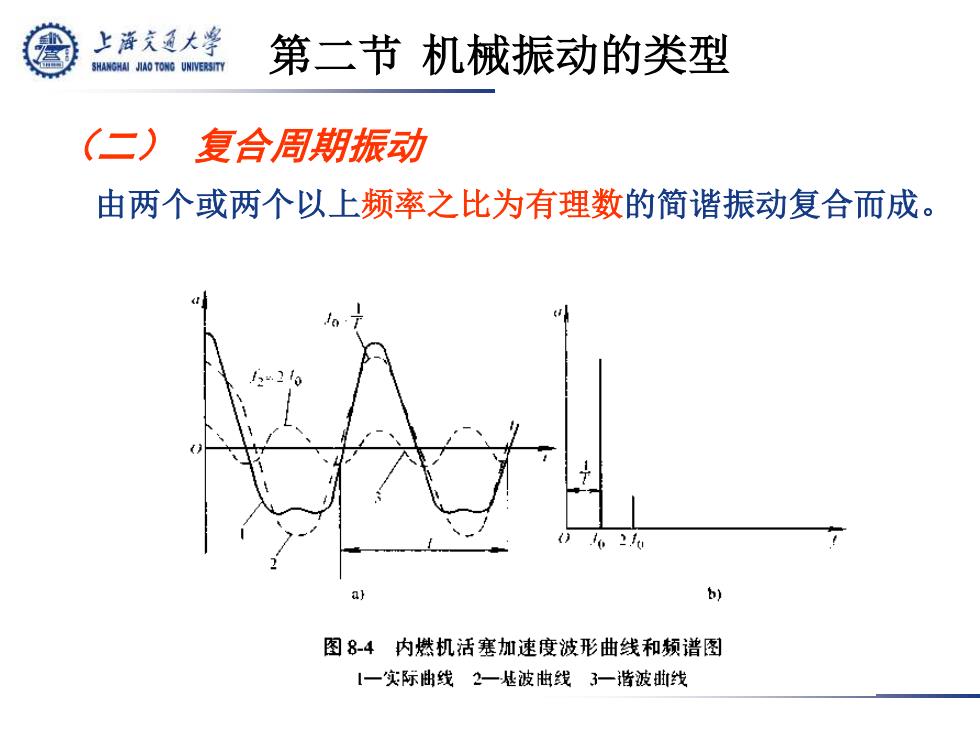
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 (二) 复合周期振动 由两个或两个以上频率之比为有理数的简谐振动复合而成。 图84内燃机活塞加速度波形曲线和频谱图 一实际出线2一基波曲线3一谐波曲线
(二) 复合周期振动 由两个或两个以上频率之比为有理数的简谐振动复合而成。 第二节 机械振动的类型