
The Fournal of FINANCE VoL.XIX SEPTEMBER 1964 No.3 CAPITAL ASSET PRICES:A THEORY OF MARKET EQUILIBRIUM UNDER CONDITIONS OF RISK* WILLIAM F.SHARPE I.INTRODUCTION ONE OF THE PROBLEMs which has plagued those attempting to predict the behavior of capital markets is the absence of a body of positive micro- economic theory dealing with conditions of risk.Although many useful insights can be obtained from the traditional models of investment under conditions of certainty,the pervasive influence of risk in financial trans- actions has forced those working in this area to adopt models of price behavior which are little more than assertions.A typical classroom ex- planation of the determination of capital asset prices,for example, usually begins with a careful and relatively rigorous description of the process through which individual preferences and physical relationships interact to determine an equilibrium pure interest rate.This is generally followed by the assertion that somehow a market risk-premium is also determined,with the prices of assets adjusting accordingly to account for differences in their risk. A useful representation of the view of the capital market implied in such discussions is illustrated in Figure 1.In equilibrium,capital asset prices have adjusted so that the investor,if he follows rational procedures (primarily diversification),is able to attain any desired point along a capital market line.1 He may obtain a higher expected rate of return on his holdings only by incurring additional risk.In effect,the market presents him with two prices:the price of time,or the pure interest rate (shown by the intersection of the line with the horizontal axis)and the price of risk,the additional expected return per unit of risk borne (the reciprocal of the slope of the line). *A great many people provided comments on early versions of this paper which led to major improvements in the exposition.In addition to the referees,who were most helpful,the author wishes to express his appreciation to Dr.Harry Markowitz of the RAND Corporation,Professor Jack Hirshleifer of the University of California at Los Angeles,and to Professors Yoram Barzel,George Brabb,Bruce Johnson,Walter Oi and R.Haney Scott of the University of Washington. Associate Professor of Operations Research,University of Washington. 1.Although some discussions are also consistent with a non-linear (but monotonic)curve. 425 This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
The journal of FINANCE VOL. XIX SEPTEMBER 1964 No. 3 CAPITAL ASSET PRICES: A THEORY OF MARKET EQUILIBRIUM UNDER CONDITIONS OF RISK* WILLIAM F. SHARPEt I. INTRODUCTION ONE OF THE PROBLEMS which has plagued those attempting to predict the behavior of capital markets is the absence of a body of positive micro- economic theory dealing with conditions of risk. Although many useful insights can be obtained from the traditional models of investment under conditions of certainty, the pervasive influence of risk in financial trans- actions has forced those working in this area to adopt models of price behavior which are little more than assertions. A typical classroom ex- planation of the determination of capital asset prices, for example, usually begins with a careful and relatively rigorous description of the process through which individual preferences and physical relationships interact to determine an equilibrium pure interest rate. This is generally followed by the assertion that somehow a market risk-premium is also determined, with the prices of assets adjusting accordingly to account for differences in their risk. A useful representation of the view of the capital market implied in such discussions is illustrated in Figure 1. In equilibrium, capital asset prices have adjusted so that the investor, if he follows rational procedures (primarily diversification), is able to attain any desired point along a capital market line.' He may obtain a higher expected rate of return on his holdings only by incurring additional risk. In effect, the market presents him with two prices: the price of time, or the pure interest rate (shown by the intersection of the line with the horizontal axis) and the price of risk, the additional expected return per unit of risk borne (the reciprocal of the slope of the line). * A great many people provided comments on early versions of this paper which led to major improvements in the exposition. In addition to the referees, who were most helpful, the author wishes to express his appreciation to Dr. Harry Markowitz of the RAND Corporation, Professor Jack Hirshleifer of the University of California at Los Angeles, and to Professors Yoram Barzel, George Brabb, Bruce Johnson, Walter Oi and R. Haney Scott of the University of Washington. t Associate Professor of Operations Research, University of Washington. 1. Although some discussions are also consistent with a non-linear (but monotonic) curve. 425 This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms
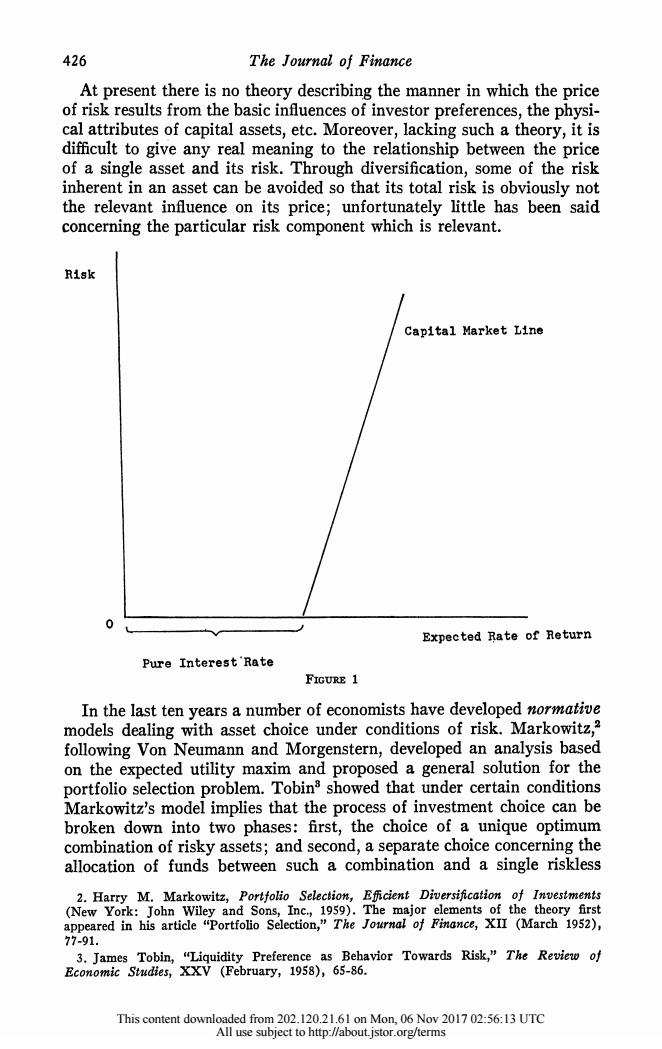
426 The Journal of Finance At present there is no theory describing the manner in which the price of risk results from the basic influences of investor preferences,the physi- cal attributes of capital assets,etc.Moreover,lacking such a theory,it is difficult to give any real meaning to the relationship between the price of a single asset and its risk.Through diversification,some of the risk inherent in an asset can be avoided so that its total risk is obviously not the relevant influence on its price;unfortunately little has been said concerning the particular risk component which is relevant. Risk Capital Market Line Expected Rate of Return Pure Interest'Rate FIGURE 1 In the last ten years a number of economists have developed normative models dealing with asset choice under conditions of risk.Markowitz,? following Von Neumann and Morgenstern,developed an analysis based on the expected utility maxim and proposed a general solution for the portfolio selection problem.Tobin3 showed that under certain conditions Markowitz's model implies that the process of investment choice can be broken down into two phases:first,the choice of a unique optimum combination of risky assets;and second,a separate choice concerning the allocation of funds between such a combination and a single riskless 2.Harry M.Markowitz,Portfolio Selection,Eficient Diversification of Investments (New York:John Wiley and Sons,Inc,1959).The major elements of the theory first appeared in his article "Portfolio Selection,"The Journal of Finance,XII (March 1952), 77-91. 3.James Tobin,"Liquidity Preference as Behavior Towards Risk,"The Review of Economic Studies,XXV (February,1958),65-86. This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
426 The Journal of Finance At present there is no theory describing the manner in which the price of risk results from the basic influences of investor preferences, the physi- cal attributes of capital assets, etc. Moreover, lacking such a theory, it is difficult to give any real meaning to the relationship between the price of a single asset and its risk. Through diversification, some of the risk inherent in an asset can be avoided so that its total risk is obviously not the relevant influence on its price; unfortunately little has been said concerning the particular risk component which is relevant. Risk Capital Market Line 0 Expected Rate of Return Pure Interest'Rate FIGURE 1 In the last ten years a number of economists have developed normative models dealing with asset choice under conditions of risk. Markowitz,2 following Von Neumann and Morgenstern, developed an analysis based on the expected utility maxim and proposed a general solution for the portfolio selection problem. Tobin' showed that under certain conditions Markowitz's model implies that the process of investment choice can be broken down into two phases: first, the choice of a unique optimum combination of risky assets; and second, a separate choice concerning the allocation of funds between such a combination and a single riskless 2. Harry M. Markowitz, Portfolio Selection, Efficient Diversification of Investments (New York: John Wiley and Sons, Inc., 1959). The major elements of the theory first appeared in his article "Portfolio Selection," The Journal of Finance, XII (March 1952), 77-91. 3. James Tobin, "Liquidity Preference as Behavior Towards Risk," The Review of Economic Studies, XXV (February, 1958), 65-86. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms

Capital Asset Prices 427 asset.Recently,Hicks has used a model similar to that proposed by Tobin to derive corresponding conclusions about individual investor behavior,dealing somewhat more explicitly with the nature of the condi- tions under which the process of investment choice can be dichotomized. An even more detailed discussion of this process,including a rigorous proof in the context of a choice among lotteries has been presented by Gordon and Gangolli.5 Although all the authors cited use virtually the same model of investor behavior,none has yet attempted to extend it to construct a market equilibrium theory of asset prices under conditions of risk.7 We will show that such an extension provides a theory with implications consistent with the assertions of traditional financial theory described above.Moreover, it sheds considerable light on the relationship between the price of an asset and the various components of its overall risk.For these reasons it warrants consideration as a model of the determination of capital asset prices. Part II provides the model of individual investor behavior under con- ditions of risk.In Part III the equilibrium conditions for the capital market are considered and the capital market line derived.The implica- tions for the relationship between the prices of individual capital assets and the various components of risk are described in Part IV. II.OPTIMAL INVESTMENT POLICY FOR THE INDIVIDUAL The Investor's Preference Function Assume that an individual views the outcome of any investment in probabilistic terms;that is,he thinks of the possible results in terms of some probability distribution.In assessing the desirability of a particular investment,however,he is willing to act on the basis of only two para- 4.John R.Hicks,"Liquidity,"The Economic Journal,LXXII (December,1962),787- 802. 5.M.J.Gordon and Ramesh Gangolli,"Choice Among and Scale of Play on Lottery Type Alternatives,"College of Business Administration,University of Rochester,1962. For another discussion of this relationship see W.F.Sharpe,"A Simplified Model for Portfolio Analysis,"Management Science,Vol.9,No.2 (January 1963),277-293.A related discussion can be found in F.Modigliani and M.H.Miller,"The Cost of Capital, Corporation Finance,and the Theory of Investment,"The American Economic Review, XLVIIⅡ(June1958),261-297. 6.Recently Hirshleifer has suggested that the mean-variance approach used in the articles cited is best regarded as a special case of a more general formulation due to Arrow.See Hirshleifer's "Investment Decision Under Uncertainty,"Papers and Proceedings of the Seventy-Sixth Annual Meeting of the American Economic Association,Dec.1963, or Arrow's "Le Role des Valeurs Boursieres pour la Repartition la Meilleure des Risques," International Colloquium on Econometrics,1952. 7.After preparing this paper the author learned that Mr.Jack L.Treynor,of Arthur D.Little,Inc.,had independently developed a model similar in many respects to the one described here.Unfortunately Mr.Treynor's excellent work on this subject is,at present, unpublished. This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
Capital Asset Prices 427 asset. Recently, Hicks4 has used a model similar to that proposed by Tobin to derive corresponding conclusions about individual investor behavior, dealing somewhat more explicitly with the nature of the condi- tions under which the process of investment choice can be dichotomized. An even more detailed discussion of this process, including a rigorous proof in the context of a choice among lotteries has been presented by Gordon and Gangolli.5 Although all the authors cited use virtually the same model of investor behavior,6 none has yet attempted to extend it to construct a market equilibrium theory of asset prices under conditions of risk. We will show that such an extension provides a theory with implications consistent with the assertions of traditional financial theory described above. Moreover, it sheds considerable light on the relationship between the price of an asset and the various components of its overall risk. For these reasons it warrants consideration as a model of the determination of capital asset prices. Part II provides the model of individual investor behavior under con- ditions of risk. In Part III the equilibrium conditions for the capital market are considered and the capital market line derived. The implica- tions for the relationship between the prices of individual capital assets and the various components of risk are described in Part IV. II. OPTIMAL INVESTMENT POLICY FOR THE INDIVIDUAL The Investor's Preference Function Assume that an individual views the outcome of any investment in probabilistic terms; that is, he thinks of the possible results in terms of some probability distribution. In assessing the desirability of a particular investment, however, he is willing to act on the basis of only two para- 4. John R. Hicks, "Liquidity," The Economic Journal, LXXII (December, 1962), 787- 802. 5. M. J. Gordon and Ramesh Gangolli, "Choice Among and Scale of Play on Lottery Type Alternatives," College of Business Administration, University of Rochester, 1962. For another discussion of this relationship see W. F. Sharpe, "A Simplified Model for Portfolio Analysis," Management Science, Vol. 9, No. 2 (January 1963), 277-293. A related discussion can be found in F. Modigliani and M. H. Miller, "The Cost of Capital, Corporation Finance, and the Theory of Investment," The American Economic Review, XLVIII (June 1958), 261-297. 6. Recently Hirshleifer has suggested that the mean-variance approach used in the articles cited is best regarded as a special case of a more general formulation due to -Arrow. See Hirshleifer's "Investment Decision Under Uncertainty," Papers and Proceedings of the Seventy-Sixth Annual Meeting of the American Economic Association, Dec. 1963, or Arrow's "Le Role des Valeurs Boursieres pour la Repartition la Meilleure des Risques," International Colloquium on Econometrics, 1952. 7. After preparing this paper the author learned that Mr. Jack L. Treynor, of Arthur D. Little, Inc., had independently developed a model similar in many respects to the one described here. Unfortunately Mr. Treynor's excellent work on this subject is, at present, unpublished. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms

428 The Journal of Finance meters of this distribution-its expected value and standard deviation.s This can be represented by a total utility function of the form: U=f(Ew;w) where Ew indicates expected future wealth and ow the predicted standard deviation of the possible divergence of actual future wealth from Ew. Investors are assumed to prefer a higher expected future wealth to a lower value,ceteris paribus (dU/dEw>0).Moreover,they exhibit risk-aversion,choosing an investment offering a lower value of ow to one with a greater level,given the level of Ew (dU/dow<0).These as- sumptions imply that indifference curves relating Ew and cw will be upward-sloping. To simplify the analysis,we assume that an investor has decided to commit a given amount (Wi)of his present wealth to investment.Letting We be his terminal wealth and R the rate of return on his investment: R=W:一W Wi we have Wt=R Wi+Wi. This relationship makes it possible to express the investor's utility in terms of R,since terminal wealth is directly related to the rate of return: U=g(EE,OR). Figure 2 summarizes the model of investor preferences in a family of indifference curves;successive curves indicate higher levels of utility as one moves down and/or to the right.10 8.Under certain conditions the mean-variance approach can be shown to lead to unsatisfactory predictions of behavior.Markowitz suggests that a model based on the semi-variance (the average of the squared deviations below the mean)would be preferable; in light of the formidable computational problems,however,he bases his analysis on the variance and standard deviation. 9.While only these characteristics are required for the analysis,it is generally assumed that the curves have the property of diminishing marginal rates of substitution between Ew and ow as do those in our diagrams. 10.Such indifference curves can also be derived by assuming that the investor wishes to maximize expected utility and that his total utility can be represented by a quadratic function of R with decreasing marginal utility.Both Markowitz and Tobin present such a derivation.A similar approach is used by Donald E.Farrar in The Investment Decision Under Uncertainty (Prentice-Hall,1962).Unfortunately Farrar makes an error in his derivation;he appeals to the Von-Neumann-Morgenstern cardinal utility axioms to trans- form a function of the form: E(U)=a+bEg一cEa2一coh2 into one of the form: E(U)=k1Er一k20r2. That such a transformation is not consistent with the axioms can readily be seen in this form,since the first equation implies non-linear indifference curves in the Eg,oB2 plane while the second implies a linear relationship.Obviously no three (different)points can lie on both a line and a non-linear curve (with a monotonic derivative).Thus the two functions must imply different orderings among alternative choices in at least some instance This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms
428 The Journal of Finance meters of this distribution-its expected value and standard deviation.8 This can be represented by a total utility function of the form: U = f(E,, a,) where Ew indicates expected future wealth and cw the predicted standard deviation of the possible divergence of actual future wealth from Ew. Investors are assumed to prefer a higher expected future wealth to a lower value, ceteris paribus (dU/dEw > 0). Moreover, they exhibit risk-aversion, choosing an investment offering a lower value of aw to one with a greater level, given the level of Ew (dU/dow < 0). These as- sumptions imply that indifference curves relating Ew and co will be upward-sloping.9 To simplify the analysis, we assume that an investor has decided to commit a given amount (WI) of his present wealth to investment. Letting Wt be his terminal wealth and R the rate of return on his investment: R Wt Wi WI we have Wt R WI + Wi. This relationship makes it possible to express the investor's utility in terms of R, since terminal wealth is directly related to the rate of return: U = g(ER, OR) . Figure 2 summarizes the model of investor preferences in a family of indifference curves; successive curves indicate higher levels of utility as one moves down and/or to the right.10 8. Under certain conditions the mean-variance approach can be shown to lead to unsatisfactory predictions of behavior. Markowitz suggests that a model based on the semi-variance (the average of the squared deviations below the mean) would be preferable; in light of the formidable computational problems, however, he bases his analysis on the variance and standard deviation. 9. While only these characteristics are required for the analysis, it is generally assumed that the curves have the property of diminishing marginal rates of substitution between EW and aw, as do those in our diagrams. 10. Such indifference curves can also be derived by assuming that the investor wishes to maximize expected utility and that his total utility can be represented by a quadratic function of R with decreasing marginal utility. Both Markowitz and Tobin present such a derivation. A similar approach is used by Donald E. Farrar in The Investment Decision Under Uncertainty (Prentice-Hall, 1962). Unfortunately Farrar makes an error in his derivation; he appeals to the Von-Neumann-Morgenstern cardinal utility axioms to trans- form a function of the form: E(U) = a+ bER - cER2 -CR2 into one of the form: E (U) = k1 E -k2aR2. That such a transformation is not consistent with the axioms can readily be seen in this form, since the first equation implies non-linear indifference curves in the ER' aR2 plane while the second implies a linear relationship. Obviously no three (different) points can lie on both a line and a non-linear curve (with a monotonic derivative). Thus the two functions must imply different orderings among alternative choices in at least some instance. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms
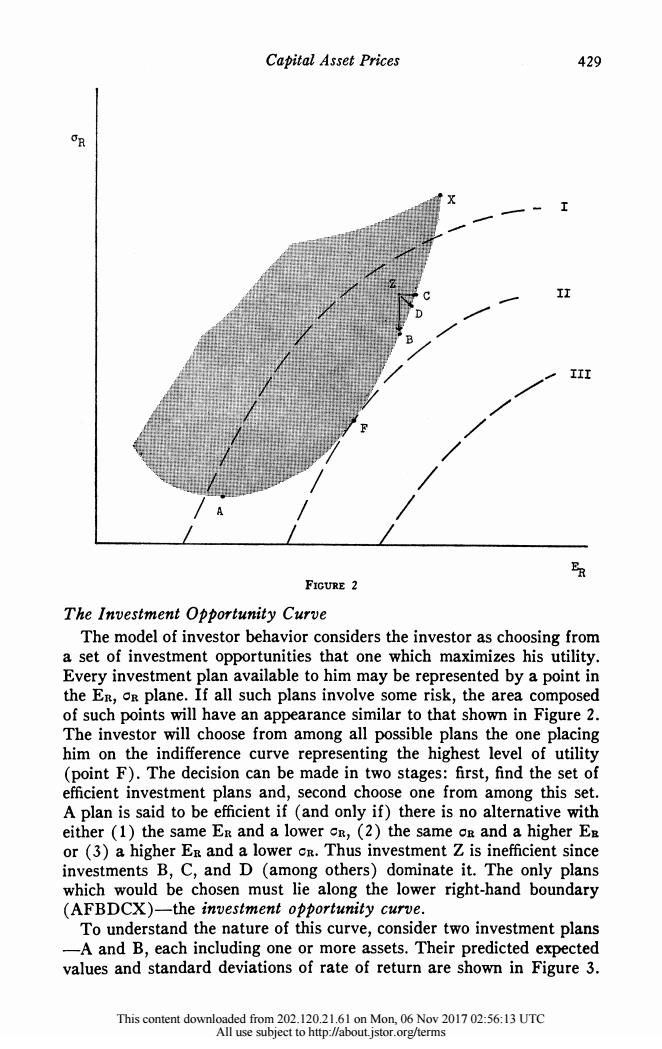
Capital Asset Prices 429 II III FIGURE 2 The Investment Opportunity Curve The model of investor behavior considers the investor as choosing from a set of investment opportunities that one which maximizes his utility. Every investment plan available to him may be represented by a point in the Er,os plane.If all such plans involve some risk,the area composed of such points will have an appearance similar to that shown in Figure 2. The investor will choose from among all possible plans the one placing him on the indifference curve representing the highest level of utility (point F).The decision can be made in two stages:first,find the set of efficient investment plans and,second choose one from among this set. A plan is said to be efficient if (and only if)there is no alternative with either (1)the same Er and a lower cr,(2)the same on and a higher E or (3)a higher Er and a lower cr.Thus investment Z is inefficient since investments B,C,and D (among others)dominate it.The only plans which would be chosen must lie along the lower right-hand boundary (AFBDCX)-the investment opportunity curve. To understand the nature of this curve,consider two investment plans -A and B,each including one or more assets.Their predicted expected values and standard deviations of rate of return are shown in Figure 3. This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
Capital Asset Prices 429 CYR The~. Ineten poruiy uv /he .. or // -7..... Thset ofinvestment opportuniti ures htoewihmsm shsuiiy Every investment plan available to him may be represented by a point in the ER, OR plane. If all such plans involve some risk, the area composed of such points will have an appearance similar to that shown in Figure 2. The investor will choose from among all possible plans the one placing him on the indifference curve representing the highest level of utility (point F). The decision can be made in two stages: first, find the set of efficient investment plans and, second choose one from among this set. A plan is said to be efficient if (and only if) there is no alternative with either (1) the same ER and a lower CR, (2) the same OR and a higher EB or (3) a higher ER and a lower CR. Thus investment Z is inefficient since investments B, C, and D (among others) dominate it. The only plans which would be chosen must lie along the lower right-hand boundary (AFBDCX)- the investment opportunity curve. To understand the nature of this curve, consider two investment plans -A and B, each including one or more assets. Their predicted expected values and standard deviations of rate of return are shown in Figure 3. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms
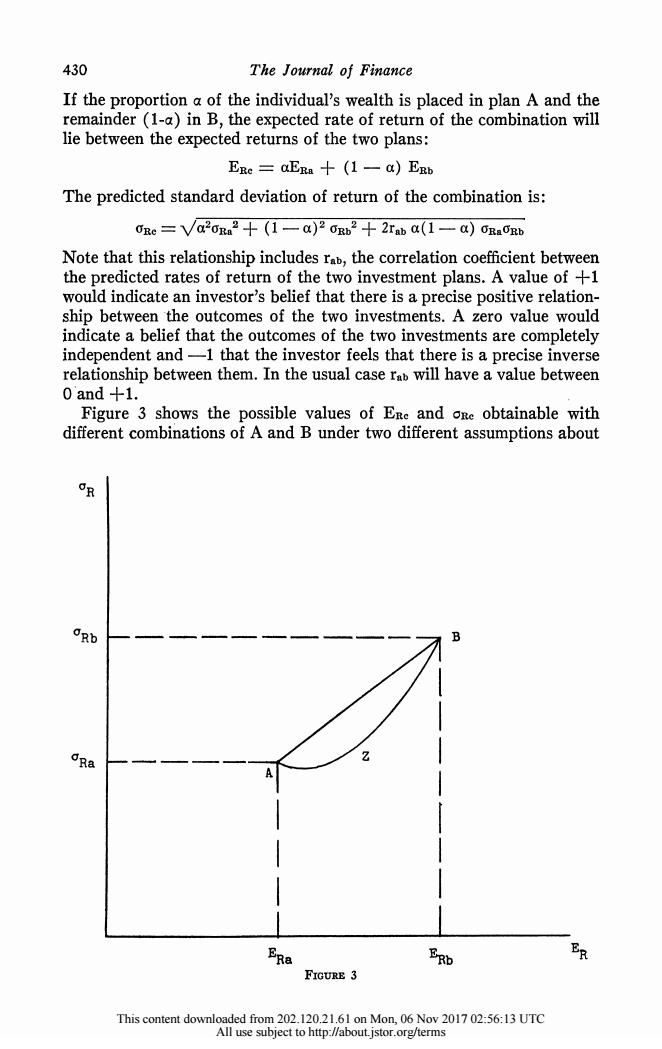
430 The Journal of Finance If the proportion a of the individual's wealth is placed in plan A and the remainder(1-a)in B,the expected rate of return of the combination will lie between the expected returns of the two plans: ERe=aERa十(1一a)ERb The predicted standard deviation of return of the combination is: 0Re=Va2ora2十(1一a)20rb2+2raba(1一a)Ragb Note that this relationship includes rab,the correlation coefficient between the predicted rates of return of the two investment plans.A value of +1 would indicate an investor's belief that there is a precise positive relation- ship between the outcomes of the two investments.A zero value would indicate a belief that the outcomes of the two investments are completely independent and-1 that the investor feels that there is a precise inverse relationship between them.In the usual case rab will have a value between 0 and +1. Figure 3 shows the possible values of Ere and oRe obtainable with different combinations of A and B under two different assumptions about oRb 0R3 Z pRo 如 FIGURE 3 This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
430 The Journal of Finance If the proportion a of the individual's wealth is placed in plan A and the remainder (1-a) in B, the expected rate of return of the combination will lie between the expected returns of the two plans: ER= aERa + (1 a) ERb The predicted standard deviation of return of the combination is: RC Va2Ra 2 + (1 a)2 Rb2 + 2rab a(1 - a) CRaORb Note that this relationship includes rab, the correlation coefficient between the predicted rates of return of the two investment plans. A value of +1 would indicate an investor's belief that there is a precise positive relation- ship between 'the outcomes of the two investments. A zero value would indicate a belief that the outcomes of the two investments are completely independent and -1 that the investor feels that there is a precise inverse relationship between them. In the usual case rab will have a value between o and +1. Figure 3 shows the possible values of ERc and ORC obtainable with different combinations of A and B under two different assumptions about OR aRb -B CRa- I I l I I I ERa ERb ER FIGURE 3 This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms

Capital Asset Prices 431 the value of rab.If the two investments are perfectly correlated,the combinations will lie along a straight line between the two points,since in this case both ERe and one will be linearly related to the proportions invested in the two plans.If they are less than perfectly positively cor- related,the standard deviation of any combination must be less than that obtained with perfect correlation (since rab will be less);thus the combi- nations must lie along a curve below the line AB.12 AZB shows such a curve for the case of complete independence (rab=0);with negative correlation the locus is even more U-shaped.18 The manner in which the investment opportunity curve is formed is relatively simple conceptually,although exact solutions are usually quite difficult.14 One first traces curves indicating Er,on values available with simple combinations of individual assets,then considers combinations of combinations of assets.The lower right-hand boundary must be either linear or increasing at an increasing rate (d2 on/dE2R>0).As suggested earlier,the complexity of the relationship between the characteristics of individual assets and the location of the investment opportunity curve makes it difficult to provide a simple rule for assessing the desirability of individual assets,since the effect of an asset on an investor's over-all investment opportunity curve depends not only on its expected rate of return (ER)and risk (cR),but also on its correlations with the other available opportunities (ru,r2,....,r).However,such a rule is implied by the equilibrium conditions for the model,as we will show in part IV. The Pure Rate of Interest We have not yet dealt with riskless assets.Let P be such an asset;its risk is zero (cEp=0)and its expected rate of return,Erp,is equal (by definition)to the pure interest rate.If an investor places a of his wealth 11. ERe=ERa十(I一a)ERb=ERb+(ERa一ER,)a ORe=Va20B 2+(1-a)2 ORb2+2Tab a(1-a)GRa Ogb but rab=1,therefore the expression under the square root sign can be factored: oRe=V儿a0Ra+((1-a)r, =a ORa +(1-a)ORb =Rb+(CRa一ORb)a 12.This curvature is,in essence,the rationale for diversification. ORa 13.When rab =0,the slope of the curve at point A is- -at point B it is ERb一ER ORb -When rab=-1,the curve degenerates to two straight lines to a point ERb一ER on the horizontal axis. 14.Markowitz has shown that this is a problem in parametric quadratic programming. An efficient solution technique is described in his article,"The Optimization of a Quadratic Function Subject to Linear Constraints,"Naval Research Logistics Quarterly,Vol.3 (March and June,1956),111-133.A solution method for a special case is given in the author's "A Simplified Model for Portfolio Analysis,"op.cit. This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
Capital Asset Prices 431 the value of rab. If the two investments are perfectly correlated, the combinations will lie along a straight line between the two points, since in this case both ERC and oRc will be linearly related to the proportions invested in the two plans.11 If they are less than perfectly positively cor- related, the standard deviation of any combination must be less than that obtained with perfect correlation (since rab will be less); thus the combi- nations must lie along a curve below the line AB."2 AZB shows such a curve for the case of complete independence (rab - 0); with negative correlation the locus is even more U-shaped.13 The manner in which the investment opportunity curve is formed is relatively simple conceptually, although exact solutions are usually quite difficult.14 One first traces curves indicating ER, OR values available with simple combinations of individual assets, then considers combinations of combinations of assets. The lower right-hand boundary must be either linear or increasing at an increasing rate (d2 CR/dE2R> 0). As suggested earlier, the complexity of the relationship between the characteristics of individual assets and the location of the investment opportunity curve makes it difficult to provide a simple rule for assessing the desirability of individual assets, since the effect of an asset on an investor's over-all investment opportunity curve depends not only on its expected rate of return (ERI) and risk (CR1), but also on its correlations with the other available opportunities (rii, rI2 ...., rin). However, such a rule is implied by the equilibrium conditions for the model, as we will show in part IV. The Pure Rate of Interest We have not yet dealt with riskless assets. Let P be such an asset; its risk is zero (oRp = 0) and its expected rate of return, ERR, is equal (by definition) to the pure interest rate. If an investor places a of his wealth 11. ERC = aERa + (1 -a) ERb = ERb + (ERa ERb) ORC = V/a2Ra2 + (1- a)2 cvRb2 + 2rab a(1 - a) rRa aRb butab 1, therefore the expression under the square root sign can be factored: YRc = \/[aaRa + (1 GO) cRb]2 - a YRa + (1 - a) aRb - 0Rb + (OYRa - YRb) a 12. This curvature is, in essence, the rationale for diversification. 13. When rab = 0, the slope of the curve at point A is - , at point B it is ERb - ERa YRb . When rab =-1, the curve degenerates to two straight lines to a point ERb- ERa on the horizontal axis. 14. Markowitz has shown that this is a problem in parametric quadratic programming. An efficient solution technique is described in his article, "The Optimization of a Quadratic Function Subject to Linear Constraints," Naval Research Logistics Quarterly, Vol. 3 (March and June, 1956), 111-133. A solution method for a special case is given in the author's "A Simplified Model for Portfolio Analysis," op. cit. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms
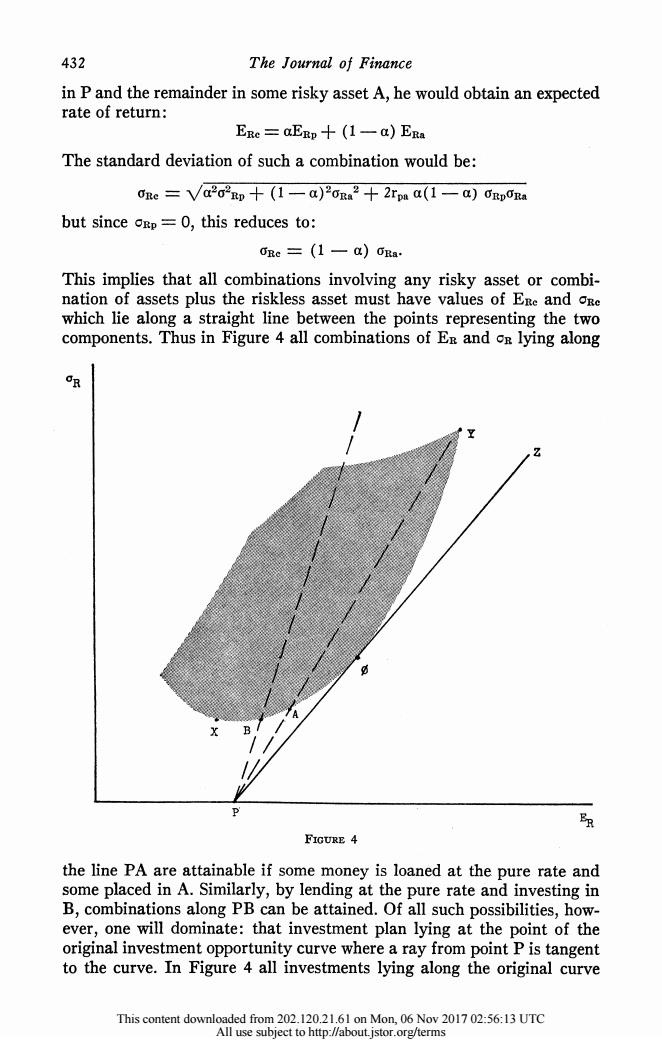
432 The Journal of Finance in P and the remainder in some risky asset A,he would obtain an expected rate of return: ERe=aEp十(1一a)ERa The standard deviation of such a combination would be: cre=Va2o2o十(1-am)2ora2十2raa(1-a)0Rpra but since oEp=0,this reduces to: rc=(1一a)Ra This implies that all combinations involving any risky asset or combi- nation of assets plus the riskless asset must have values of Ere and cRe which lie along a straight line between the points representing the two components.Thus in Figure 4 all combinations of En and cs lying along FIGURE 4 the line PA are attainable if some money is loaned at the pure rate and some placed in A.Similarly,by lending at the pure rate and investing in B,combinations along PB can be attained.Of all such possibilities,how- ever,one will dominate:that investment plan lying at the point of the original investment opportunity curve where a ray from point P is tangent to the curve.In Figure 4 all investments lying along the original curve This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
432 The Journal of Finance in P and the remainder in some risky asset A, he would obtain an expected rate of return: ERC= aERP + (1 - a) ER1a The standard deviation of such a combination would be: 0Rc - V\a202Rp + ( -a)2aua2 + 2rpa a(1-a) (}RplRa but since ORp = 0, this reduces to: CrR = (1 a) (Ra. This implies that all combinations involving any risky asset or combi- nation of assets plus the riskless asset must have values of ERC and OCR which lie along a straight line between the points representing the two components. Thus in Figure 4 all combinations of ER and OR lying along OaR P' 'v FIGURiE 4 the line PA are attainable 'if some money is loaned at the pure rate and some pBlaced in A. Similarly, by lending at the pure rate and investing in B, combinations along PB can be attained. Of all such possibilities, how- ever, one will dominate: that investment plan lying at the point of the original investment opprortunity curve where a ray from point P is tangent to the curve. In Figure 4 all investments lying along the original curve This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms

Capital Asset Prices 433 from X to are dominated by some combination of investment in and lending at the pure interest rate. Consider next the possibility of borrowing.If the investor can borrow at the pure rate of interest,this is equivalent to disinvesting in P.The effect of borrowing to purchase more of any given investment than is possible with the given amount of wealth can be found simply by letting a take on negative values in the equations derived for the case of lending. This will obviously give points lying along the extension of line PA if borrowing is used to purchase more of A;points lying along the extension of PB if the funds are used to purchase B,etc. As in the case of lending,however,one investment plan will dominate all others when borrowing is possible.When the rate at which funds can be borrowed equals the lending rate,this plan will be the same one which is dominant if lending is to take place.Under these conditions,the invest- ment opportunity curve becomes a line (PZ in Figure 4).Moreover, if the original investment opportunity curve is not linear at point,the process of investment choice can be dichotomized as follows:first select the (unique)optimum combination of risky assets (point )and second borrow or lend to obtain the particular point on PZ at which an indiffer- ence curve is tangent to the line.15 Before proceeding with the analysis,it may be useful to consider alter- native assumptions under which only a combination of assets lying at the point of tangency between the original investment opportunity curve and a ray from P can be efficient.Even if borrowing is impossible,the investor will choose(and lending)if his risk-aversion leads him to a point below on the line P.Since a large number of investors choose to place some of their funds in relatively risk-free investments,this is not an un- likely possibility.Alternatively,if borrowing is possible but only up to some limit,the choice of would be made by all but those investors willing to undertake considerable risk.These alternative paths lead to the main conclusion,thus making the assumption of borrowing or lending at the pure interest rate less onerous than it might initially appear to be. III.EQUILIBRIUM IN THE CAPITAL MARKET In order to derive conditions for equilibrium in the capital market we invoke two assumptions.First,we assume a common pure rate of interest, with all investors able to borrow or lend funds on equal terms.Second, we assume homogeneity of investor expectations:16 investors are assumed 15.This proof was first presented by Tobin for the case in which the pure rate of interest is zero (cash).Hicks considers the lending situation under comparable conditions but does not allow borrowing.Both authors present their analysis using maximization subject to constraints expressed as equalities.Hicks'analysis assumes independence and thus insures that the solution will include no negative holdings of risky assets;Tobin's covers the general case,thus his solution would generally include negative holdings of some assets.The discussion in this paper is based on Markowitz'formulation,which includes non-negativity constraints on the holdings of all assets. 16.A term suggested by one of the referees. This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
Capital Asset Prices 433 from X to cP are dominated by some combination of investment in 4 and lending at the pure interest rate. Consider next the possibility of borrowing. If the investor can borrow at the pure rate of interest, this is equivalent to disinvesting in P. The effect of borrowing to purchase more of any given investment than is possible with the given amount of wealth can be found simply by letting a take on negative values in the equations derived for the case of lending. This will obviously give points lying along the extension of line PA if borrowing is used to purchase more of A; points lying along the extension of PB if the funds are used to purchase B, etc. As in the case of lending, however, one investment plan will dominate all others when borrowing is possible. When the rate at which funds can be borrowed equals the lending rate, this plan will be the same one which is dominant if lending is to take place. Under these conditions, the invest- ment opportunity curve becomes a line (POZ in Figure 4). Moreover, if the original investment opportunity curve is not linear at point c, the process of investment choice can be dichotomized as follows: first select the (unique) optimum combination of risky assets (point c), and second borrow or lend to obtain the particular point on PZ at which an indiffer- ence curve is tangent to the line.'5 Before proceeding with the analysis, it may be useful to consider alter- native assumptions under which only a combination of assets lying at the point of tangency between the original investment opportunity curve and a ray from P can be efficient. Even if borrowing is impossible, the investor will choose 4 (and lending) if his risk-aversion leads him to a point below 4) on the line Pq). Since a large number of investors choose to place some of their funds in relatively risk-free investments, this is not an un- likely possibility. Alternatively, if borrowing is possible but only up to some limit, the choice of 4) would be made by all but those investors willing to undertake considerable risk. These alternative paths lead to the main conclusion, thus making the assumption of borrowing or lending at the pure interest rate less onerous than it might initially appear to be. III. EQUILIBRIUM IN THE CAPITAL MARKET In order to derive conditions for equilibrium in the capital market we invoke two assumptions. First, we assume a common pure rate of interest, with all investors able to borrow or lend funds on equal terms. Second, we assume homogeneity of investor expectations:16 investors are assumed 15. This proof was first presented by Tobin for the case in which the pure rate of interest is zero (cash). Hicks considers the lending situation under comparable conditions but does not allow borrowing. Both authors present their analysis using maximization subject to constraints expressed as equalities. Hicks' analysis assumes independence and thus insures that the solution will include no negative holdings of risky assets; Tobin's covers the general case, thus his solution would generally include negative holdings of some assets. The discussion in this paper is based on Markowitz' formulation, which includes non-negativity constraints on the holdings of all assets. 16. A term suggested by one of the referees. This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms

434 The Journal of Finance to agree on the prospects of various investments-the expected values standard deviations and correlation coefficients described in Part II. Needless to say,these are highly restrictive and undoubtedly unrealistic assumptions.However,since the proper test of a theory is not the realism of its assumptions but the acceptability of its implications,and since these assumptions imply equilibrium conditions which form a major part of classical financial doctrine,it is far from clear that this formulation should be rejected-especially in view of the dearth of alternative models leading to similar results. Under these assumptions,given some set of capital asset prices,each investor will view his alternatives in the same manner.For one set of prices the alternatives might appear as shown in Figure 5.In this situa- OR Cl C2 CL 1 B4 M FIGURE 5 tion,an investor with the preferences indicated by indifference curves A through As would seek to lend some of his funds at the pure interest rate and to invest the remainder in the combination of assets shown by point since this would give him the preferred over-all position A*.An investor with the preferences indicated by curves Bi through B would seek to in- vest all his funds in combination while an investor with indifference curves Ci through Cs would invest all his funds plus additional (borrowed) This content downloaded from 202.120.21.61 on Mon,06 Nov 2017 02:56:13 UTC All use subject to http://about.istor.org/terms
434 The Journal of Finance to agree on the prospects of various investments-the expected values, standard deviations and correlation coefficients described in Part II. Needless to say, these are highly restrictive and undoubtedly unrealistic assumptions. However, since the proper test of a theory is not the realism of its assumptions but the acceptability of its implications, and since these assumptions imply equilibrium conditions which form a major part of classical financial doctrine, it is far from clear that this formulation should be rejected-especially in view of the dearth of alternative models leading to similar results. Under these assumptions, given some set of capital asset prices, each investor will view his alternatives in the same manner. For one set of prices the alternatives might appear as shown in Figure 5. In this situa- aR Cl C2 - -C3 C1/ / B ~~ B~2 1/ / A3 P ER FIGURE 5 tion an investor with the preferences indicated by indifference curves A1 through A4 would seek to lend some of his funds at the pure interest rate and to invest the remainder in the combination of assets shown by point 4,0 since this would give him the preferred over-all position A*. An investor with the preferences indicated by curves B1 through B4 would seek to in- vest all his funds in combination 4, while an investor with indifference curves C1 through C4 would invest all his funds plus additional (borrowed) This content downloaded from 202.120.21.61 on Mon, 06 Nov 2017 02:56:13 UTC All use subject to http://about.jstor.org/terms