兰州交通大学：《数控技术及编程》课程教学资源（教案讲义）05

数控技术及应用教案及讲稿 上部分：数控技术及编程 第五讲 一、备课教案 适用专业机械设计制造及其自动化讲次 第五讲 上课 时间 年月日节 第二章计算机数控系统 第二节计算机数控系统的基本原理 五.插补原理 学 内 3.脉冲增量插补（行程标量插补） 容 提 (2)DDA法直线插补 纲 及 能够运用DDA法进行直线插补和 (3)DDA法圆弧插补 要 圆弧插补计算：理解数字增量插 补（时间标量插补）中插补周期 4.数字增量插补（时间标量插补 与速度、精度的关系和直线插补 算法 (1)插补周期与速度、精度的关系 (2)直线插补算法 教学实施手段 效果记录 课堂讲授 √ 重 插补周期与速度、精度的关系和止 课堂讨论 点 线插补算法。 现场示教 小结讲评 难 增量括 其它 插补周期与速度、 精度的关系和直 点 线插补算法 教具 CAI,黑板 推预 陈德道主编数控技术及应用北京 荐复 参习 国防工业出版社，2009 学 考任 董玉红主编机床数控技术哈尔滨 书务哈尔滨工业大学出版社2003 记 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 1 第五讲 一、备课教案 适用专业 机械设计制造及其自动化 讲次 第五讲 上课 时间 年 月 日 节 教 学 内 容 提 纲 及 要 求 第二章 计算机数控系统 第二节 计算机数控系统的基本原理 . 五．插补原理 3．脉冲增量插补（行程标量插补） 能够运用DDA法进行直线插补和 圆弧插补计算；理解数字增量插 补（时间标量插补）中插补周期 与速度、精度的关系和直线插补 算法 （2）DDA 法直线插补 （3）DDA 法圆弧插补 4．数字增量插补（时间标量插补） （1）插补周期与速度、精度的关系 （2）直线插补算法 重 点 DDA 法进行直线插补和圆弧插补； 数字增量插补（时间标量插补）中 插补周期与速度、精度的关系和直 线插补算法。 教学实施手段 效果记录 课堂讲授 √ 课堂讨论 √ 现场示教 小结讲评 难 点 DDA 法进行直线插补和圆弧插补； 数字增量插补（时间标量插补）中 插补周期与速度、精度的关系和直 线插补算法。 其 它 教具 CAI，黑板 推 预 荐 复 参 习 考 任 书 务 陈德道主编.数控技术及应用.北京: 国防工业出版社,2009 董玉红主编.机床数控技术.哈尔滨: 哈尔滨工业大学出版社,2003 教 学 后 记

数控技术及应用教案及讲稿 上部分：数控技术及编程 二、讲稿 第二章计算机数控系统 第二节计算机数控系统的基本原理 (2)DDA法直线插补 对于平面直线进行插补，如图2-20所示的直线0E,起点在原点，终点坐标为 (x,y),令v表示动点移动速度，,y,分别表示动点在X轴和Y轴方向的分速度 根据积分公式，在XY轴上的微小位移量△x,△y应为 △r=y,Ar △y=y,△M L=Vx+月 L 因而有 V:=Kxe =K 坐标轴的位移增量为 △r=Kx.M △y=Ky.△1 各坐标轴的位移量为 X-jkx.dl-Kx-K Y=jK.=K2yM=K∑ 上式中取△1=1，由此可作直线插补器，如图2-21所示。直线插补器由两个数字积分器 组成，其被积函数寄存器中存放终点坐标值x,和y。,山相当于插补控制源发出的控制 信号。每发出一个插补脉冲△，控制被积函数x和y.向各自的积分累加器相加一次。 设累加器为n位，容量为2”（最大存为2”1），取K=。,当x、y计数满2"时必然发 生溢出。如果将x,累m次以后X的积分值应为 该数的整数部分表示溢出的脉冲数，余数部分存放在累加器中。这种关系还可以表 示为： 积分值=溢出脉冲数+余数 当两个坐标方向X、Y同时插补时，用溢出脉冲控制机床进给就可以加工出所需要的直 兰州交通大学机电工程学院 2

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 2 二、讲稿 第二章 计算机数控系统 第二节 计算机数控系统的基本原理 （2） DDA 法直线插补 对于平面直线进行插补，如图 2-20 所示的直线 OE，起点在原点，终点坐标为 （ e e x , y ），令 v 表示动点移动速度， x y v , v 分别表示动点在 X 轴和 Y 轴方向的分速度， 根据积分公式，在 XY 轴上的微小位移量 x,y 应为 L y v v L x v v L x y y v t x v t y e x e e e y x = = = +  =   =  2 2 因而有 L v K v Ky v Kx y e x e = = = 坐标轴的位移增量为 y Ky t x Kx t e e  =   =  各坐标轴的位移量为       = = = = = =  = = =  = n i n i e e e t n i e n i e e t Y Ky dt K y t K y X Kx dt K x t K x 0 1 1 0 1 1 上式中取 t =1，由此可作直线插补器，如图 2-21 所示。直线插补器由两个数字积分器 组成，其被积函数寄存器中存放终点坐标值 e x 和 e y ，t 相当于插补控制源发出的控制 信号。每发出一个插补脉冲 t ，控制被积函数 e x 和 e y 向各自的积分累加器相加一次。 设累加器为 n 位,容量为 n 2 （最大存为 n 2 -1），取 K n 2 = 1 ，当 x、y 计数满 n 2 时必然发 生溢出。如果将 e x 累 m 次以后 X 的积分值应为 n e m i n xe mx X 1 2 2 =  = = 该数的整数部分表示溢出的脉冲数，余数部分存放在累加器中。这种关系还可以表 示为： 积分值=溢出脉冲数+余数 当两个坐标方向 X、Y 同时插补时，用溢出脉冲控制机床进给就可以加工出所需要的直

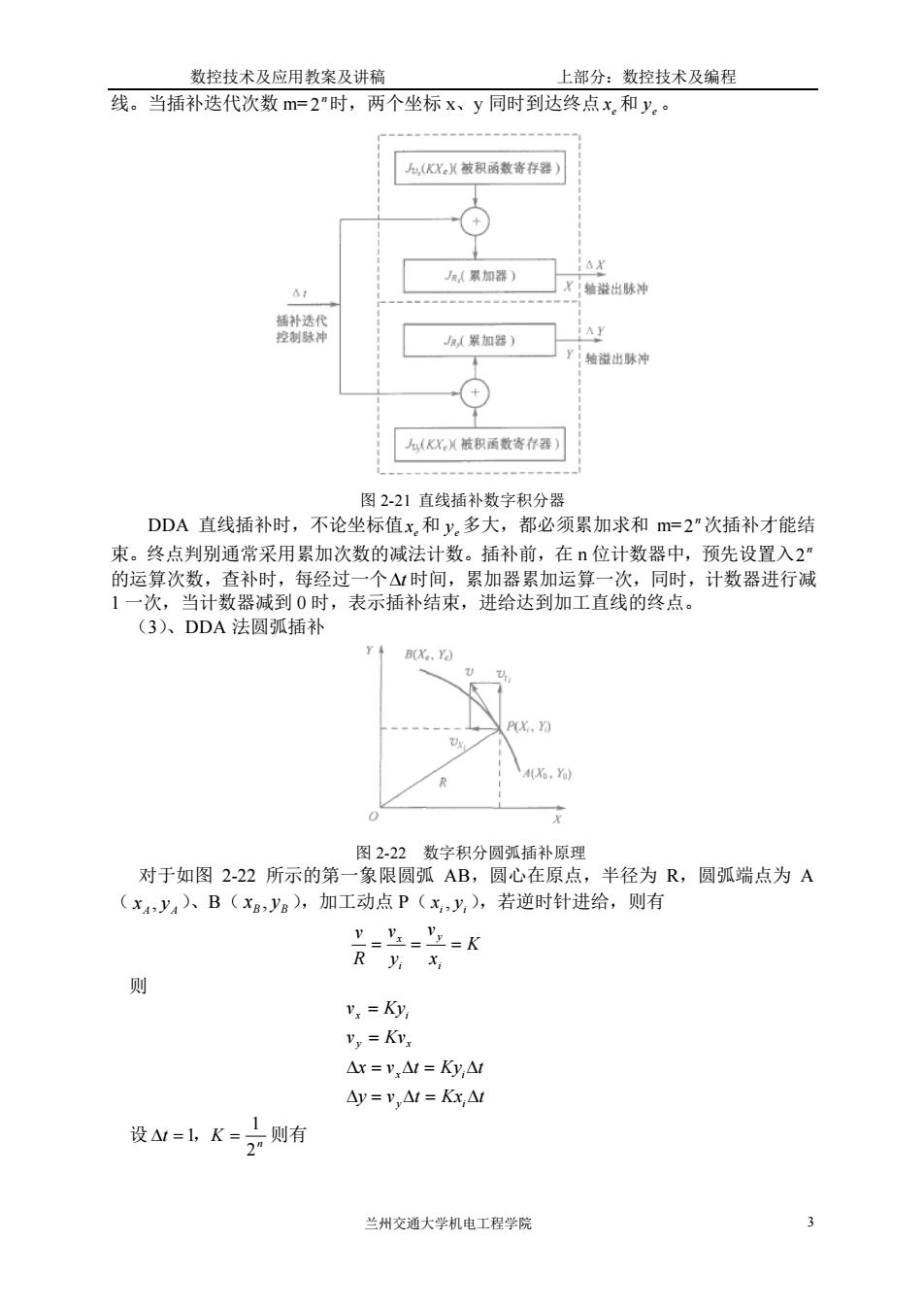
数控技术及应用教案及讲稿 上部分：数控技术及编程 线。当插补迭代次数m=2”时，两个坐标x、y同时到达终点x,和y。 (:X被积函数寄存器) (加器) A X!轴滋出脉冲 Y滋出脉冲 九(X,(被积函数寄存器】 图2-21直线插补数字积分器 DDA直线插补时，不论坐标值x,和y,多大，都必须累加求和m=2"次插补才能结 束。终点判别通常采用累加次数的减法计数。插补前，在位计数器中，预先设置入2 的运算次数，查补时，每经过一个△M时间，累加器累加运算一次，同时，计数器进行减 1一次，当计数器减到0时，表示插补结束，进给达到加工直线的终点。 (3、DDA法圆弧插补 B(X.Ye) 图2-22数字积分圆弧插补原理 对于如图2-22所示的第一象限圆弧AB,圆心在原点，半径为R,圆弧端点为A （x4,ya)、B(xayg),加工动点P（x,y),若逆时针进给，则有 y v:-Y=K 则 V:=Ky ,=K △x=y△M=Ky,M 4y=",A=K,△1 设N=1太=士则有 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 3 线。当插补迭代次数 m= n 2 时，两个坐标 x、y 同时到达终点 e x 和 e y 。 图 2-21 直线插补数字积分器 DDA 直线插补时，不论坐标值 e x 和 e y 多大，都必须累加求和 m= n 2 次插补才能结 束。终点判别通常采用累加次数的减法计数。插补前，在 n 位计数器中，预先设置入 n 2 的运算次数，查补时，每经过一个 t 时间，累加器累加运算一次，同时，计数器进行减 1 一次，当计数器减到 0 时，表示插补结束，进给达到加工直线的终点。 （3）、DDA 法圆弧插补 图 2-22 数字积分圆弧插补原理 对于如图 2-22 所示的第一象限圆弧 AB，圆心在原点，半径为 R，圆弧端点为 A （ A A x , y ）、B（ B B x , y ），加工动点 P（ i i x , y ），若逆时针进给，则有 K x v y v R v i y i x = = = 则 y v t Kx t x v t Ky t v Kv v Ky y i x i y x x i  =  =   =  =  = = 设 n t K 2 1  = 1， = 则有

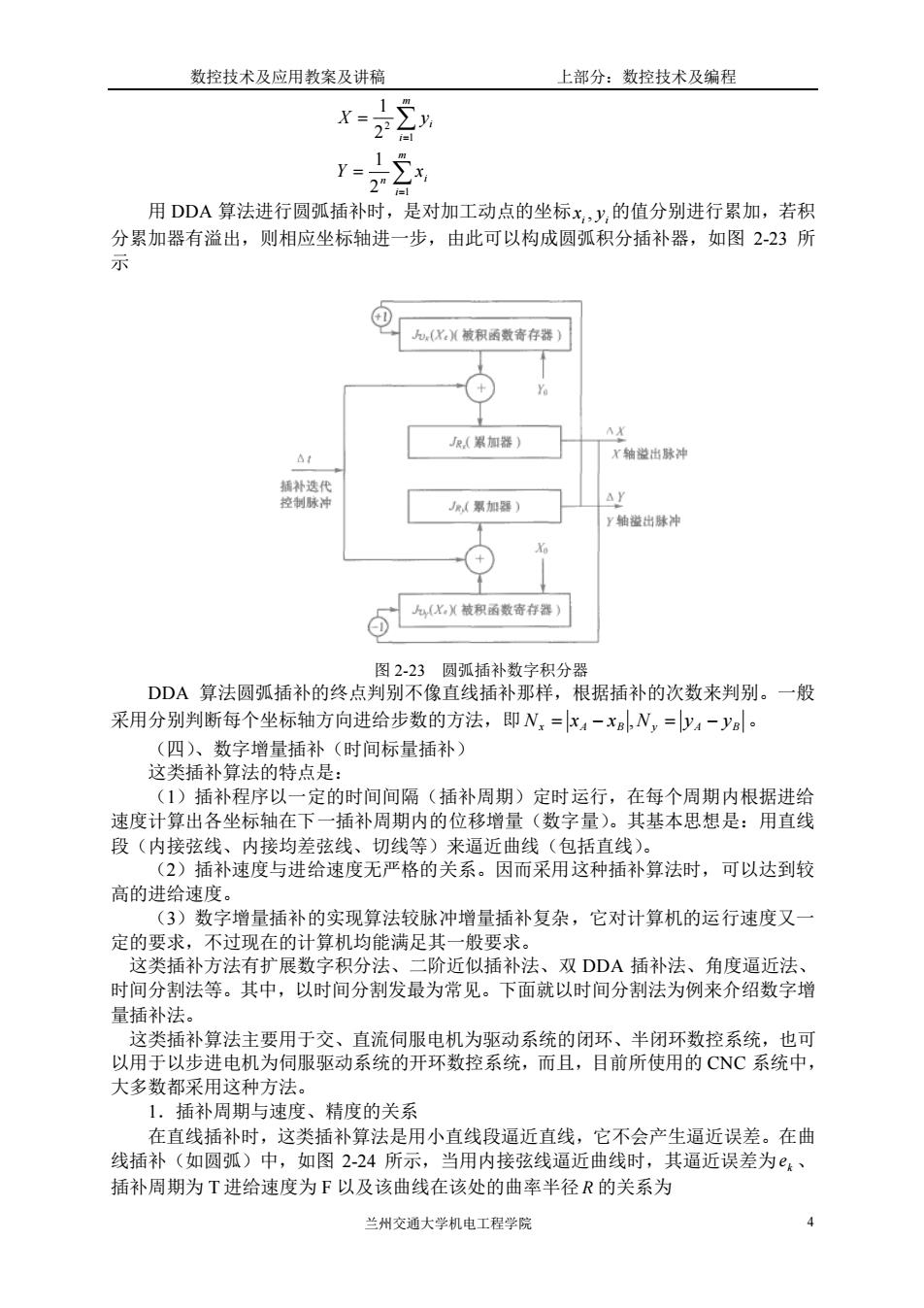
数控技术及应用教案及讲稿 上部分：数控技术及编程 x-2 用DDA算法进行圆弧插补时，是对加工动点的坐标x,y,的值分别进行累加，若积 累加器有溢出，则相应坐标轴进一步，由此可以构成圆弧积分插补器，如图2-23所 示 包化X被限春装者存鞋】 (+ AX e(累加器) X轴脱出脉神 (累加) AY Y轴型出珠冲 4(化，X被积函数寄存器) 图2.23圆插补数字积分 DDA算法圆弧插补的终点判别不像直线插补那样，根据插补的次数来判别。一般 采用分别判断每个坐标轴方向进给步数的方法，即N,=x4一x,N,=y4一y。 特点是 (1)插补程序以一定的时间间隔（插补周期）定时运行，在每个周期内根据进给 速度计算出各坐标轴在下一插补周期内的位移增量（数字量）。其基本思想是：用直线 段（内接弦线、内接均差弦线、切线等）来逼近曲线（包括直线）。 (2)插补速度与进给速度无严格的关系。因而采用这种插补算法时，可以达到较 高的进给速 (3)数字增量插补的实现算法较脉冲增量插补复杂，它对计算机的运行速度又一 定的要求，不过现在的计算机均能满足其一般要求。 这类插补方法有扩展数字积分法、二阶近似插补法、双DDA插补法、角度逼近法、 时间分割法等。其中，以时间分割发最为常见。下面就以时间分割法为例来介绍数字增 量插补法。 这类插补算法主要用于交、直流伺服电机为驱 动系统的闭环、半闭环数控系统 也可 以用于以步进电机为伺服驱动系统的开环数控系统，而且，目前所使用的CC系统中， 大多数都采用这种方法。 1.插补周期与速度、精度的关系 插补周期为T进给速度为F以及该曲线在该处的曲率半径R的关系为 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 4   = = = = m i n i m i i Y x X y 1 1 2 2 1 2 1 用 DDA 算法进行圆弧插补时，是对加工动点的坐标 i i x , y 的值分别进行累加，若积 分累加器有溢出，则相应坐标轴进一步，由此可以构成圆弧积分插补器，如图 2-23 所 示 图 2-23 圆弧插补数字积分器 DDA 算法圆弧插补的终点判别不像直线插补那样，根据插补的次数来判别。一般 采用分别判断每个坐标轴方向进给步数的方法，即 x A B y A B N = x − x ,N = y − y 。 （四）、数字增量插补（时间标量插补） 这类插补算法的特点是： （1）插补程序以一定的时间间隔（插补周期）定时运行，在每个周期内根据进给 速度计算出各坐标轴在下一插补周期内的位移增量（数字量）。其基本思想是：用直线 段（内接弦线、内接均差弦线、切线等）来逼近曲线（包括直线）。 （2）插补速度与进给速度无严格的关系。因而采用这种插补算法时，可以达到较 高的进给速度。 （3）数字增量插补的实现算法较脉冲增量插补复杂，它对计算机的运行速度又一 定的要求，不过现在的计算机均能满足其一般要求。 这类插补方法有扩展数字积分法、二阶近似插补法、双 DDA 插补法、角度逼近法、 时间分割法等。其中，以时间分割发最为常见。下面就以时间分割法为例来介绍数字增 量插补法。 这类插补算法主要用于交、直流伺服电机为驱动系统的闭环、半闭环数控系统，也可 以用于以步进电机为伺服驱动系统的开环数控系统，而且，目前所使用的 CNC 系统中， 大多数都采用这种方法。 1．插补周期与速度、精度的关系 在直线插补时，这类插补算法是用小直线段逼近直线，它不会产生逼近误差。在曲 线插补（如圆弧）中，如图 2-24 所示，当用内接弦线逼近曲线时，其逼近误差为 k e 、 插补周期为 T 进给速度为 F 以及该曲线在该处的曲率半径 R 的关系为

数控技术及应用教案及讲稿 上部分：数控技术及编程 图2-24用内接弦线逼进圆弧 6 由于狠小则 △L=FT 248R8R 由此可知，插补周期T与进给速度F、逼近误差e以及曲率半径R有关。当F、R 定时，T越小，e,也越小：当R、e一定时，T越小，容许的进给速度越大。从这个 意义上讲，T越小越好，但是T的选择将受到插补运算时间、位置控制周期以及系统 CPU等的限制。在实际CNC系统中，T是固定的，而F、R用户给定的，所以编程时 要根据最大容许误差,、以及圆弧半径R来选择进给速度F。 2.直线插补算法 在设计直线插补程序时，为了简化程序的设计，通常将插补计算坐标系的原点选在 被插补直线的起点，如图所示，设有一直线OP,O(0,O)为起点，P(x, )为终点， 要求以速度F(mm/min),沿着OP进给，设系统插补周期为T(ms),则在T内的合成 进给两为△L(m)为 Y P(y.) p,(x,y）△ 、B a 图2-25时间分割法直线插补 兰州交通大学机电工程学院

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 5 图 2-24 用内接弦线逼进圆弧 R FT R L L L L FT R L L ek 8 ( ) 4 2 4 8 tan 2 4 4 tan 4 tan 2 2 2 =   =    =  =   =  =         由于 很小则 由此可知，插补周期 T 与进给速度 F、逼近误差 k e 以及曲率半径 R 有关。当 F、R 一定时，T 越小， k e 也越小；当 R、 k e 一定时，T 越小，容许的进给速度越大。从这个 意义上讲，T 越小越好，但是 T 的选择将受到插补运算时间、位置控制周期以及系统 CPU 等的限制。在实际 CNC 系统中，T 是固定的，而 F、R 用户给定的，所以编程时 要根据最大容许误差 k e 、以及圆弧半径 R 来选择进给速度 F。 2．直线插补算法 在设计直线插补程序时，为了简化程序的设计，通常将插补计算坐标系的原点选在 被插补直线的起点，如图所示，设有一直线 OP，O（0,0）为起点，P（ e e x , y ）为终点， 要求以速度 F（mm/min）,沿着 OP 进给，设系统插补周期为 T（ms），则在 T 内的合成 进给两为 L (µm)为 图 2-25 时间分割法直线插补

数控技术及应用教案及讲稿 上部分：数控技术及编程 FT AL= 60 若T=8ms则 设为P(x,y)某一插补点，P(xy)为下一插补点，则由图可知 △x,=ALcosa X=x+△x y=xi tan a Ay,=y -y 式中 tana =x cosa= x2+y2 上式算法是先求△x后计算△y,同样还可以先计算△y,后计算△x,即 Ay =ALCOs B y1=y+△y X=ya tan B △x,=x--x, 式中 CosB=y/ /√x2+ 上述哪一种算法比较好？可对他们进行如下分析： 由第一种算法可得 △y,=(x,+△x,)tana-y 由第二种算法可得 △x,=y,+Ay,)tanB-x 对上两式分别求微分，并取绝对值得 j-( 式1 a=mAa,X=4》 式2 由此可知：当xy.时 对1式有： ld△y,Kd△x 该算法对误差有收敛作用： 对2式有： 该算法对误差有放大作用。 通过上面的分析，可得出如下结论： 当x≥时，采用先算△x的方法 当xy时，采用先算△y的方法。 该结论的实质是在插补计算时总是先算大的坐标增量，后算小的坐标增量。若再考 虑不同的象限，则插补公式将有8组。为了程序设计的方便，可引入引导坐标的概念， 即在采样周期内，将进给增量值较大的坐标定义为引导坐标G,进给增量值较小的坐标 定义为非引导坐标N。由于引入引导坐标的概念，便将插补计算公式归纳为一组 △G.=△Lcos B G=G,+△G N=G tan B △N,=Na-N, 兰州交通大学机电工程学院 6

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 6 60 FT L = 若 T=8ms 则 15 2F L = 设为 ( , ) i i i P x y 某一插补点， ( , ) i+1 i+1 i+1 P x y 为下一插补点，则由图可知 i i i i i i i i i y y y y x x x x x L  = − = = +   =  + + + + 1 1 1 1 tan cos   式中 e e y x tan = 2 2 cos e e e x y x +  = 上式算法是先求 i x 后计算 i y ，同样还可以先计算 i y 后计算 i x ，即 i i i i i i i i i x x x x y y y y y L  = − = = +   =  − + + + 1 1 1 1 tan cos   式中 e e x y tan  = 2 2 cos e e e x y y +  = 上述哪一种算法比较好？可对他们进行如下分析： 由第一种算法可得 i i i i y = (x + x )tan − y 由第二种算法可得 i i i i x = (y + y )tan  − x 对上两式分别求微分，并取绝对值得 ( ) tan ( ) ( ) i e e i i d x x y d y =   d x =  式 1 ( ) tan ( ) ( ) i e e i i d y y x d x =   d y =  式 2 由此可知：当 e e x  y 时 对 1 式有： ( ) ( ) i i d y  d x 该算法对误差有收敛作用； 对 2 式有： ( ) ( ) i i d x  d y 该算法对误差有放大作用。 通过上面的分析，可得出如下结论： 当 e e x  y 时，采用先算 x 的方法； 当 e e x  y 时， 采用先算 y 的方法。 该结论的实质是在插补计算时总是先算大的坐标增量，后算小的坐标增量。若再考 虑不同的象限，则插补公式将有 8 组。为了程序设计的方便，可引入引导坐标的概念， 即在采样周期内，将进给增量值较大的坐标定义为引导坐标 G，进给增量值较小的坐标 定义为非引导坐标 N。由于引入引导坐标的概念，便将插补计算公式归纳为一组 i i i i i i i i i N N N N G G G G G L  = − = = +   =  − + + + 1 1 1 1 tan cos  

数控技术及应用教案及讲稿 上部分：数控技术及编程 式中ma=6. cosa=G./ /G2+N2 在程序设计时，将上式设计成子程序，并在其输入输出部分进行引导坐标与实际坐 标的相互转换。这样可大大简化程序的设计。 兰州交通大学机电工程学院 7

数控技术及应用教案及讲稿 上部分：数控技术及编程 兰州交通大学机电工程学院 7 式中 e e G N tan = 2 2 cos e e e G N G +  = 在程序设计时，将上式设计成子程序，并在其输入输出部分进行引导坐标与实际坐 标的相互转换。这样可大大简化程序的设计