
第三章点 在几何中学过,确定一点的空同位置,用三维箭卡儿直角坐标系来描述,它是以数来精述 空间点的位置,而本寮三维空间点的位置,是用”形”来描述的,即通过投影的方法,在二维平 面上精确表达点的三维空间位置。 第一节 两投影面体系中点的投影 一、点的两面投影 为了确定点的空间位置,建立一个两投影面体系:两个互相垂直的投影平面V和H,见图 31。V面称之为正立投影面(简称正面),H面称之为水平投 影面(简称水平面)。两投影面的交线OX称为投影轴。V、H 投影面将空间分为四个区域,每个区域称之为分角,按图3】 所示顺序分别称为第一分角、第二分角、第三分角、第四分 角。我国的各种制图标准都规定使用第一分角。 设在两投影体系中有一点A,过A点分别向V、H面投 影,即过A点分别向V、H面作垂线,得到交点a'和a,则称a' 为A点的正面投影,a为A点的水平投影。 将H面绕OX轴向下旋转90°与V面重合,得到如图 图31两投影面体系 3-2b)所示的投影图。因为投影面被认为可以任意大小,所以通常将它画成如图3-2)所示的 投影图。 规定:空间点用大写字母表示,水平投影用相应的小写字母表示,正面投影用相应的小写 字母加一撇表示。 图32点的两面投影的形成 二、点在两面投影体系中的投影规律 如图32a)所示因为Ad1V面,面,所以平面aha10x轴,与0x轴交于点a,所 以a.⊥0x轴,oa10K轴。当投影体系展开时,aa0在一条垂直于Ox轴的直线上,此 .22
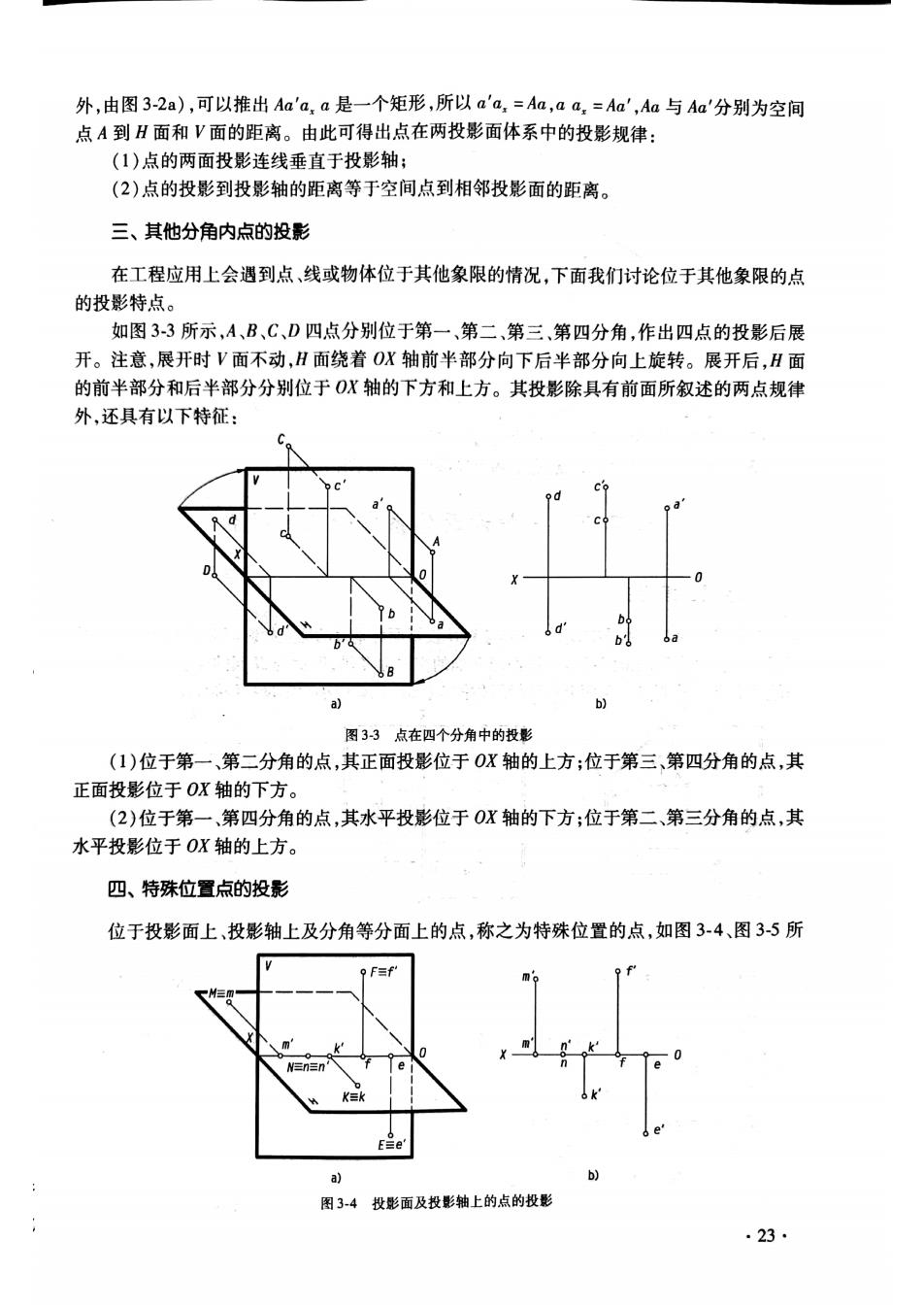
外,由图3-2a),可以推出Aa'a,a是一个矩形,所以a'a,=Aa,aa,=Ad',Au与Aa'分别为空间 点A到H面和V面的距离。由此可得出点在两投影面体系中的投影规律: (1)点的两面投影连线垂直于投影轴: (2)点的投影到投影轴的距离等于空间点到相邻投影面的距离。 三、其他分角内点的投影 在工程应用上会遇到点,线或物体位于其他象限的情况,下面我们讨论位于其他象限的点 的投影特点。 如图33所示,A、B、C、D四点分别位于第一、第二、第三,第四分角,作出四点的投影后展 开。注意,展开时V面不动,H面绕着OX轴前半部分向下后半部分向上旋转。展开后,H面 的前半部分和后半部分分别位于O轴的下方和上方。其投影除具有前面所叙述的两点规律 外,还具有以下特征: 图33点在四个分角中的投影 (1)位于第一、第二分角的点,其正面投影位于O轴的上方;位于第三、第四分角的点,其 正面投影位于Ox轴的下方。 (2)位于第一,第四分角的点,其水平投影位于O轴的下方;位于第二、第三分角的点,其 水平投影位于OX轴的上方。 四、特殊位置点的投影 位于投影面上,投影轴上及分角等分面上的点,称之为特殊位置的点,如图3-4、图3-5所 2 图34投影面及投影轴上的点的投影 .23
示。其投影特征是: 图35第二,第四分角面上的点的投影 ((1)位于投影面上的点,一个投形落在投影轴上,另一个投影与其本身重合: (2)位于投影轴上的点,两个投影均与其本身重合: (3)位于分角等分面上的点,点的两个投影至OX轴的距离相等。 第二节三投影面体系中的,点的投影 一、点的三面投影 在上述两投影面体系中,增加一个与V,H投影面都垂直的侧立投影面W(简称侧面)就构 成了三投影面体系,见图3-6a)。W面与V面的交线称Z轴,W面与H面的交线称Y轴,三投 影轴的交点O称原点。W面上点的投影称侧面投影,用相应小写字母加两撇表示。 图3-6点的三面投影的形成 展开方法如图3-6所示,其中Y轴在展开过程中分别表现在H面上(用Y标注)和W面上 (用Y标注)。 点的两面投影规律,均可应用于三面投影系统中。如图36所示,根据点的两面投影规 律,不难得出: (1)a'a"⊥0z;a'al0X;a"an⊥0Y;aa,⊥0y (2)a'a,=a"a,=Aa=A点到H面的距离; a'a,=a0,=Aa”=A点到W面的距离; aa,=a”a,=Aa'=A点V面的距离。 作图时,为使a4,=aa,采用45°斜线作为辅助线,见图3-6b)和图3-60)。 .24·

点的两面投影能唯一确定点的空间位置。已知点的两面投影,可根据投影原理用作图的 方法求出第三面投影。 【例31】已知B点的正面投影和侧面投影b,b,如图37所示,求B点的水平投影b。 bD, 图37求点的第三面投影 解:根据点的投影规律,水平投影b一定在过正面投影6'垂直于O轴的投影连线上,而 b6,=b6。 作图:过b'作线段垂直于0X轴:再过b作0Y,轴的垂线与45°斜线相交,过此交点作直线 垂直于OY轴,与过b'垂直于OX轴的直线段相交,交,点即为所求水平投影b。 二、点的投影与坐标 三维空间的点是以到三个参照面的距离来定位的。坐标是用数值来表达这三个距离;投 影法则是用图形来表达这三个距离,即投影到轴的距离。实际上,坐标与投影两种表示点的空 间位置的方法是可以互换的,工程实际中,有时也采用坐标来表示空间点的位置。 将笛卡儿坐标系引入到三投影面体系中,这时投影面就是相应的坐标面,投影轴就是相应 的坐标轴,投影体系的原点就是坐标系的原点;并规定X轴从原点向左为正,Y轴从原点向前 为正,Z轴从原点向上为正。图3-6a)A点的三个坐标分别为: x=a,0=Aa”=A点到W面的距离=a'a,=aa,(点的投影到轴的距离); y=a,0=Aa'=A点到V面的距离=aa,=a”a,(点的投影到轴的距离); z=a,0=Aa=A点到H面的距离=a'a,=a"an(点的投影到轴的距离)。 三、点的相对位置 1.两点的相对位置 空间点的位置也可以由相对另一点的位置来确定。在投影体系中两点的相对位置是这样 规定的:两点中,x坐标大的点在左,y坐标大的点在前,:坐标大的点在上。换句话说,两点 中,离W面远的点在左,离V而远的点在前,离H面远的点在上。如图3-8所示,B点在A点 的右方、后方和上方。 2.重影点及其可见性 当两点位于同一投射线上时,两点在该投射线所垂直的投影面上的投影重合成一点,此两 点称为对该投影面的重影点。 重影点的重合投影要区分可见性。我们把投射线看作人的视线,以对H面的重影点为 例:投影时相当于人眼从上往下看,上面的点投影可见:下面的点投影不可见。以此原理推断 凡离投影面远(即坐标大的点)的重影点的投影可见,即规定把不可见点的投影加括号,以区 .25
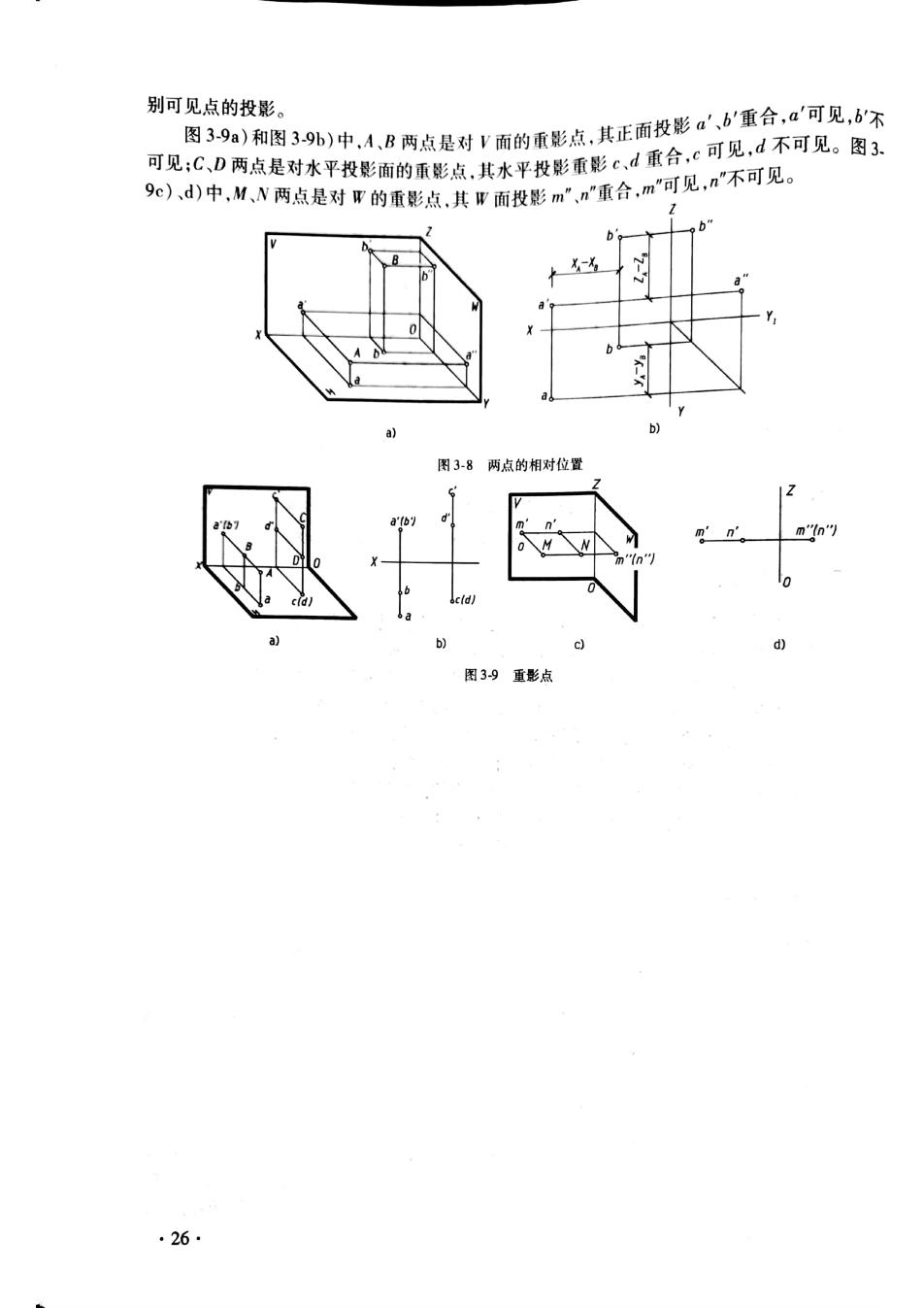
别可见点的投影。 见限3图9外中A,B两点是对Y商的系影点,其正面投影a6重合可见.不 可见:CD商点是对木平技能面的东点其术平投能食彭:1重合可见山不可见。图3。 9e),中,从,V两点是对的重点,其:我重合可见a不可见。 图38两点的相对位增 26