第3章点、直线、平面的投影
第3章 点、直线、平面的投影 第2章

本章要求 1.掌握点、线、面的投影特性及相对位置; 2.掌握直角三角形法; 3.掌握直角投影定理; 4掌握换面法及其应用
本 章 要 求 1.掌握点、线、面的投影特性及相对位置; 2.掌握直角三角形法; 3.掌握直角投影定理; 4.掌握换面法及其应用。 本章要求 本章要 求

3.1点的投影 >点在两投影面体系中的投影 >点在三投影面体系中的投影 >点的投影与其坐标的关系 >两点的相对位置
3.1 点的投影 ➢点在两投影面体系中的投影 ➢点在三投影面体系中的投影 ➢点的投影与其坐标的关系 ➢两点的相对位置
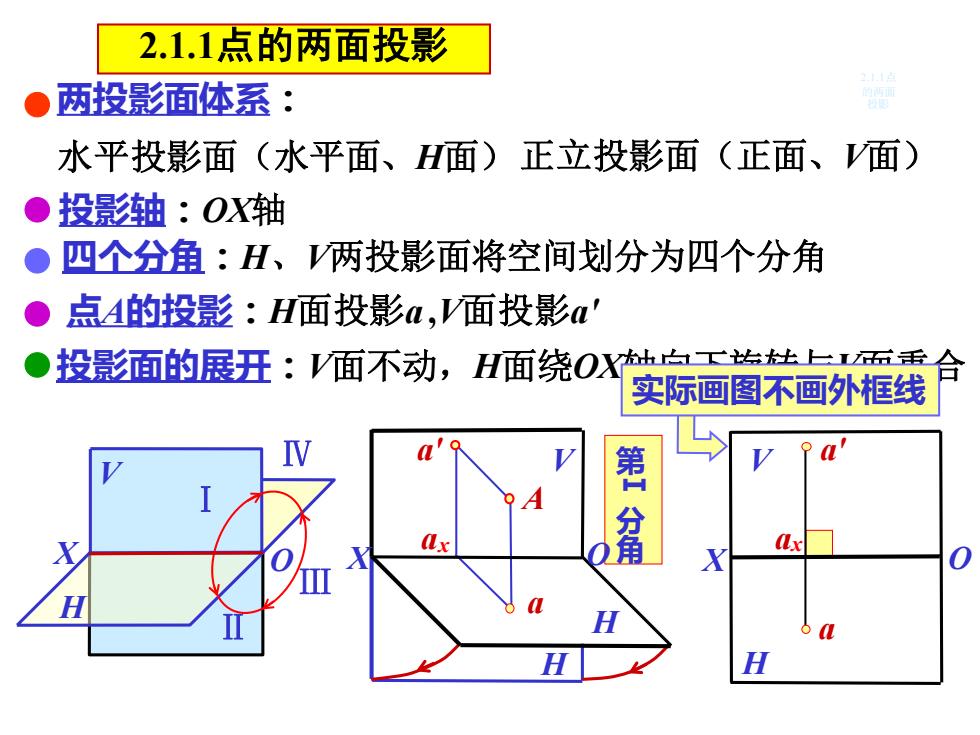
2.1.1点的两面投影 ● 两投影面体系: 水平投影面(水平面、H面)正立投影面(正面、V面) ●投影铀:OX轴 ● 四个分角:H、两投影面将空间划分为四个分角 点4的投影:H面投影a,V面投影a' ●投影面的展狂:V面不动,H面绕OX白工抬共上西秉合 实际画图不画外框线 角 (x 0 a H
2.1.1点的两面投影 两投影面体系: 投影轴:OX轴 四个分角:H、V两投影面将空间划分为四个分角 水平投影面(水平面、H面)正立投影面(正面、V面) H V Ⅳ Ⅰ Ⅱ Ⅲ a A H ax a' a 点A的投影:H面投影a ,V面投影a' 投影面的展开:V面不动,H面绕OX轴向下旋转与V面重合 H V 实际画图不画外框线 a' ax X O V H 第 Ⅰ 分 X O 角 X O 2.1.1点 的两面 投影
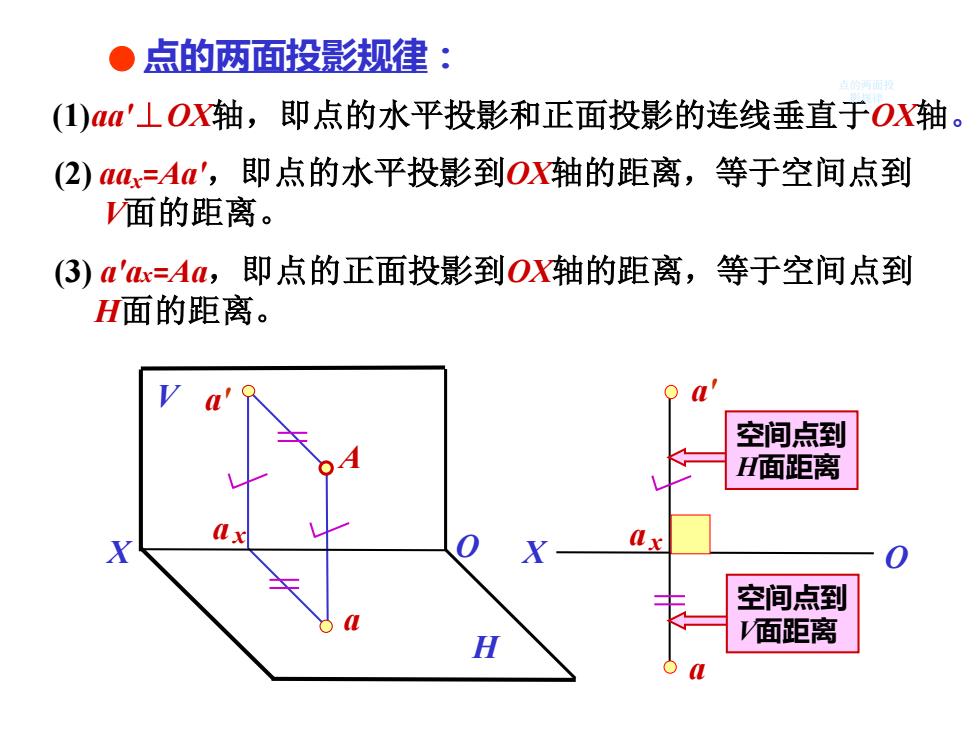
●点的两面投影规律: (1)aa'⊥OX轴,即点的水平投影和正面投影的连线垂直于OX轴。 (2)M=Aa',即点的水平投影到OX轴的距离,等于空间点到 面的距离。 (3)a'a=Aa,即点的正面投影到OX轴的距离,等于空间点到 H面的距离。 e 空间点到 H面距离 空间点到 H 面距离
点的两面投影规律: (2) aax=Aa',即点的水平投影到OX轴的距离,等于空间点到 V面的距离。 (3) a'ax=Aa,即点的正面投影到OX轴的距离,等于空间点到 H面的距离。 a x a' a a' a x 空间点到 V面距离 空间点到 H面距离 (1)aa'⊥OX轴,即点的水平投影和正面投影的连线垂直于OX轴。 a A V H X O X O 点的两面投 影规律
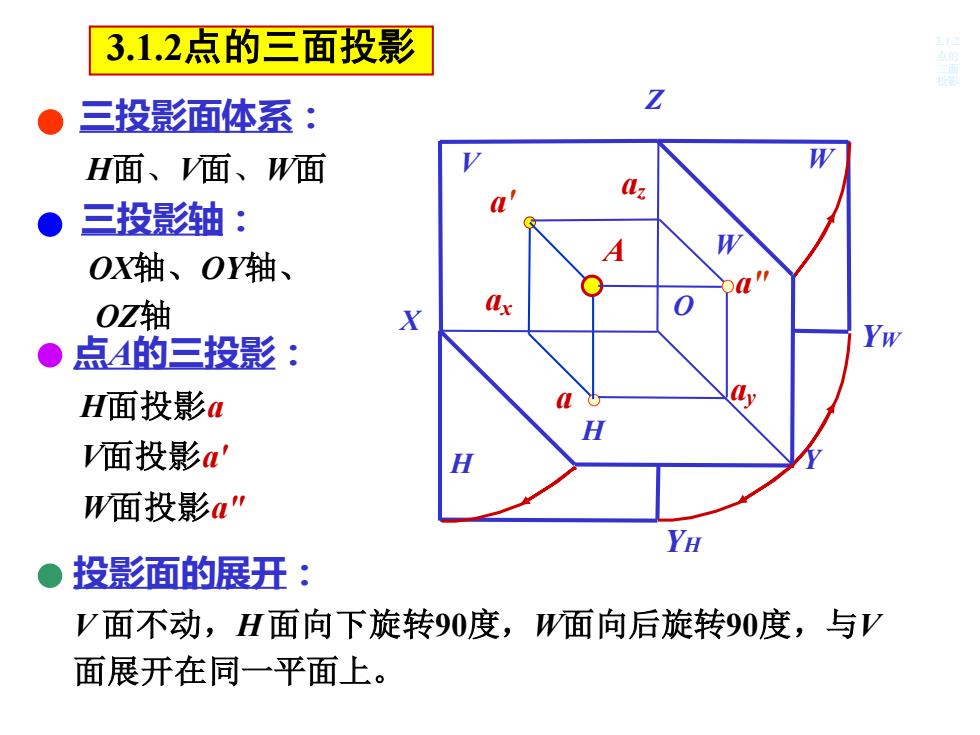
3.1.2点的三面投影 三投影面体系: Z H面、V面、W面 Az 三投影轴: A W OX轴、OY轴、 0Z轴 X ax ●点A的三投影: Yw H面投影a H 面投影a' H W面投影a" YH ●投影面的展开: V面不动,H面向下旋转90度,W面向后旋转90度,与V 面展开在同一平面上
3.1.2点的三面投影 三投影面体系: H面、V面、W面 三投影轴: OX轴、OY轴、 OZ轴 点A的三投影: H面投影a V面投影a' W面投影a" 投影面的展开: V 面不动,H 面向下旋转90度,W面向后旋转90度,与V 面展开在同一平面上。 ax a' a W O Y Z X H V W H A YH YW 2.1.2 点的 三面 投影 az ay a
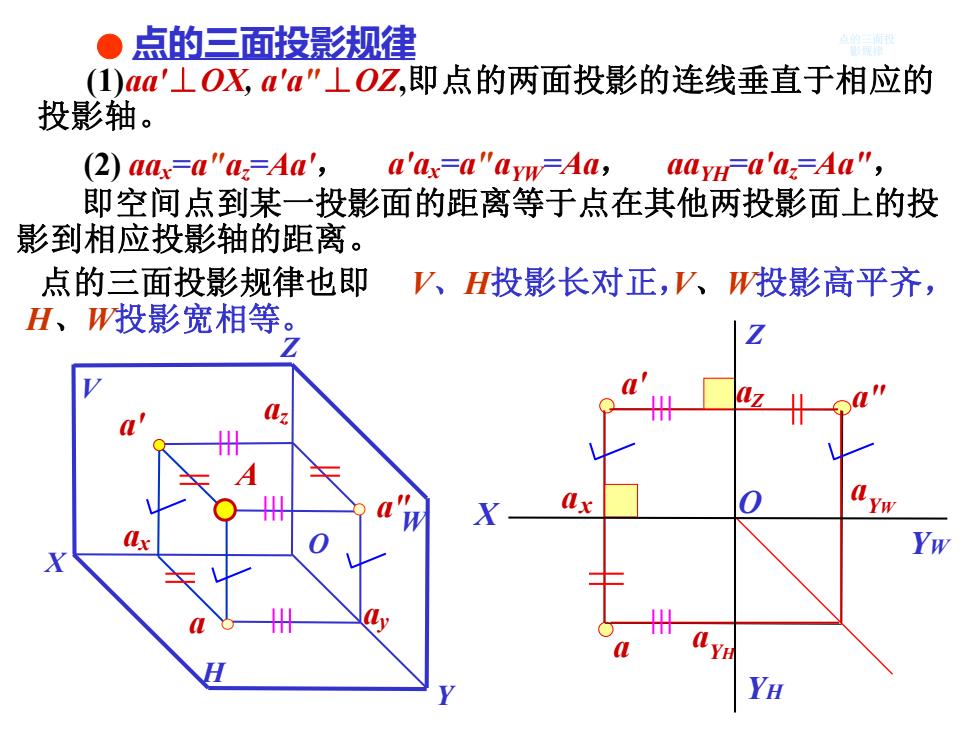
●点的三面投影规律 (1)aa'⊥OX,a'a"⊥OZ,即点的两面投影的连线垂直于相应的 投影轴。 (2)aax=a"a=Aa', a'ax=a"ayw=Aa, aayHa'a;=Aa", 即空间点到某一投影面的距离等于点在其他两投影面上的投 影到相应投影轴的距离。 点的三面投影规律也即 V、H投影长对正,V、W投影高平齐, H、W投影宽相等。 YW YH
a' a aZ a" YH a YW a (1)aa'⊥OX, a'a"⊥OZ,即点的两面投影的连线垂直于相应的 投影轴。 点的三面投影规律 即空间点到某一投影面的距离等于点在其他两投影面上的投 影到相应投影轴的距离。 点的三面投影规律也即 (2) aax =a"az =Aa', a'ax =a"aYW =Aa, aaYH =a'az =Aa", V、H投影长对正,V、W投影高平齐, H、W投影宽相等。 点的三面投 影规律 az ay ax a"W H V O Y Z X a' a A ax YH YW X O Z
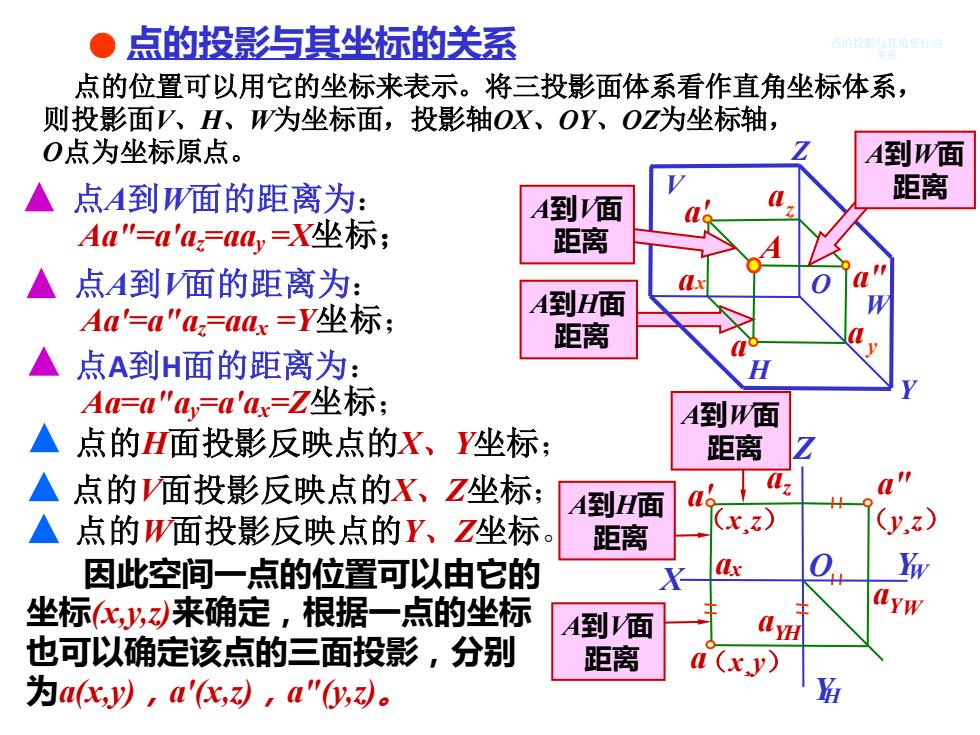
● 点的投影与其坐标的送系 点的位置可以用它的坐标来表示。将三投影面体系看作直角坐标体系, 则投影面V、H、W为坐标面,投影轴OX、OY、OZ为坐标轴, O点为坐标原点。 A到W面 ▲点A到W面的距离为: 距离 A到面 Aa"=a'a=a,=X坐标; 距离 ▲点A到面的距离为: Aa'=a"a=x=Y坐标; A到H面 距离 ▲点A到H面的距离为: A=a"a,=a'a=Z坐标; A到W面 ▲点的H面投影反映点的X、Y坐标; 距离 ▲点的V面投影反映点的X、Z坐标; z A到H面 ▲点的W面投影反映点的Y、Z坐标。 距离 (x.z) (y,z) 因此空间一点的位置可以由它的 X x 0 坐标化,,来确定,根据一点的坐标 A到面 ayH 也可以确定该点的三面投影,分别 距离 a(xy) 为ac以,ac,,a"y
(x¸z) 点的位置可以用它的坐标来表示。将三投影面体系看作直角坐标体系, 则投影面V、H、W为坐标面,投影轴OX、OY、OZ为坐标轴, O点为坐标原点。 点的投影与直角坐标的 点的投影与其坐标的关系 关系 点A到W面的距离为: Aa"=a'az=aay =X坐标; 点A到V面的距离为: Aa'=a"az=aax =Y坐标; 点A到H面的距离为: Aa=a"ay=a'ax=Z坐标; 点的H面投影反映点的X、Y坐标; 点的W面投影反映点的Y、Z坐标。 点的V面投影反映点的X、Z坐标; A到H面 距离 YH O Z YW aYH aYW az a' ax X a a" A到V面 距离 A到H面 距离 A到W面 距离 Z a a O Y z y A a' a ax V H a" W A到W面 距离 A到V面 距离 (x¸y) (y¸z) 因此空间一点的位置可以由它的 坐标(x,y,z)来确定,根据一点的坐标 也可以确定该点的三面投影,分别 为a(x,y),a'(x,z),a"(y,z)

●」 由点的两面投影求第三面投影 点的任意两面投影均包含点的三个坐标值,确定了点到三 个投影面的距离,所以点的两面投影即可唯一确定点在空间的 位置,根据一点的两面投影,可求其第三投影。 [例]已知点A的两个投影,求第三投影。 法一 法二 X YW YW YH YH 通过作45°线使 用分规直接量取 a"a,=aax a"a=aax
点的任意两面投影均包含点的三个坐标值,确定了点到三 个投影面的距离,所以点的两面投影即可唯一确定点在空间的 位置,根据一点的两面投影,可求其第三投影。 由点的两面投影求第三面投影 点的二 求三 az 法一: 法二: 用分规直接量取 a"az =aax [例] 已知点A的两个投影,求第三投影。 a" Z YH a X ax a' O YW az a" Z YH a X ax a' O YW 通过作45°线使 a"az =aax

「例]已知点A、B、C分别两面投影,求其第三面投影, 并指明其空间位置。 点A在面上0y=0, b" 即点到面的距离为0) 点B在W面上KB=0, 即点到W面的距离为0) Yw 点C在OX轴上yc=0, c0,即点到V、H面的 距离均为0) b YH
YW Z X O YH a a' b' b" c' c [例] 已知点A、B、C分别两面投影,求其第三面投影, 并指明其空间位置。 a" b c" 点A在V面上(yA=0, 即点到V面的距离为0) 点B在W面上(xB=0, 即点到W面的距离为0) 点C在OX轴上(yC=0, zC=0,即点到V、H面的 距离均为0)