
第十四章标高投影图 在士木工程中常常需要绘制地形图,以便于在图纸上描述和解决有关问题。由于地 面的形状很复杂,一般为不规则的曲面,且水平尺寸与高度尺寸相差很大,难以用多面 正投影法表达清楚,标高投影法是适于表示地形面和复查曲面的一种投影方法。 标高投影法就是取三面正投影中的水平投影图:在水平投影图上加注特征地形物上 某些特殊点、线、面的高程的方法,以高程数字代替立面图的作用。它是一种单面投影 仍然属于正投影,高程数字称为高程或标高,高程以米为单位,在图上无需注明。在士 须注明绘图比例或画出图示比例尺。 §14.1点和直线的标高投影 一、点的标高投影 在点的水平投影旁,标注出该点距离水平投影面H的高程数字,即得到该点的标高 当一点高于H面时,标高为正 其水平投影为a、b、c,在各点水平投影对应字母的右下角标上各点距离水平面的高程 数字4,0,-2,这些数字称为各点的标高。 .B ko C-3 234 1234 图141点的标搞投影 二、直线的标高投影 1、直线的表示法 (1)两点确定直线,即通过直线上两点的标高投影确定直线,如图142示直线
第十四章 标高投影图 在土木工程中常常需要绘制地形图,以便于在图纸上描述和解决有关问题。由于地 面的形状很复杂,一般为不规则的曲面,且水平尺寸与高度尺寸相差很大,难以用多面 正投影法表达清楚,标高投影法是适于表示地形面和复查曲面的一种投影方法。 标高投影法就是取三面正投影中的水平投影图;在水平投影图上加注特征地形物上 某些特殊点、线、面的高程的方法,以高程数字代替立面图的作用。它是一种单面投影, 仍然属于正投影,高程数字称为高程或标高,高程以米为单位,在图上无需注明。在土 木工程图上一般采用与测量相一致的标准海平面作为高程基准面,目前,我国采用的是 “1985 国家高程基准”。为了根据标高投影确定物体的形状和大小,在标高投影图上必 须注明绘图比例或画出图示比例尺。 §14. 1 点和直线的标高投影 一、 点的标高投影 在点的水平投影旁,标注出该点距离水平投影面 H 的高程数字,即得到该点的标高 投影。选择水平投影面 H 作为基准面,设其高程为零,当一点高于 H 面时,标高为正; 低于 H 面时,标高为负;H 面上的点的标高为零。如图 14-1 示,设空间三个点 A、B、C, 其水平投影为 a、b、c,在各点水平投影对应字母的右下角标上各点距离水平面的高程 数字 4,0,-2,这些数字称为各点的标高。 图 14-1 点的标搞投影 二、直线的标高投影 1、直线的表示法 (1)两点确定直线,即通过直线上两点的标高投影确定直线,如图 14-2 示直线

AB和CD,它们的标高投影分别为ab6和c6d2,其中CD为铅垂线。 (2)直线上一点的标高投影及直线的坡度和方向,如图142示过E点的直线,由 ÷可确定E点的空间位置,在包含过E点这条直线的铅垂面内,按着H面投影上 箭头所指出的下降方向(一般箭头指向下坡),根据坡度1就可以唯一地确定这 条直线的空间位置。 (3)水平线因平行于H面,水平线上所有点的高程都相同,所以水平线称为等高 线。等高线只要画出它的H面投影并注明其高程数,也就可以唯一地确定该等高 线的空间位置。如图14-2示直线FG, 01234 01234 图14-2直线的标高投影 2、直线的实长及确定整数高程点 在标高投影中求直线的实长,仍然采用正投影中的直角三角形法。如图14-3示 以直线的标高投影为一直角边:直线两端点的高程差为另一直角边,作直角三角形,该 直角三角形的斜边为直线的实长,α角为直线对基准面H的倾角。 在实际工作中常遇到直线的两端点的标高数字并非整数,需要在直线的投影上定出 各整数标高点,这些整数标高点称为刻度.如图144示,已知直线AB的标高投影sb6 求直线AB上的整数标高点,作图方法是在标高投影sb6,的一侧作五条任意等距与 a6,平行的平行直线,令最下一条为3个单位,令最上一条为7个单位,分别过a 和b6,作a.b67的垂线,在垂线上分别按其标高数字3.5和6.7定出A、B两点。连接 AB,AB与各
AB 和 CD,它们的标高投影分别为 a3b6 和 c6d2,其中 CD 为铅垂线。 (2)直线上一点的标高投影及直线的坡度和方向,如图 14-2 示过 E 点的直线,由 e5 可确定 E 点的空间位置,在包含过 E 点这条直线的铅垂面内,按着 H 面投影上 箭头所指出的下降方向(一般箭头指向下坡),根据坡度 i=1 就可以唯一地确定这 条直线的空间位置。 (3)水平线因平行于 H 面,水平线上所有点的高程都相同,所以水平线称为等高 线。等高线只要画出它的 H 面投影并注明其高程数,也就可以唯一地确定该等高 线的空间位置。如图 14-2 示直线 FG, 图 14-2 直线的标高投影 2、直线的实长及确定整数高程点 在标高投影中求直线的实长,仍然采用正投影中的直角三角形法。如图 14-3 示, 以直线的标高投影为一直角边;直线两端点的高程差为另一直角边,作直角三角形,该 直角三角形的斜边为直线的实长, 角为直线对基准面 H 的倾角。 在实际工作中常遇到直线的两端点的标高数字并非整数,需要在直线的投影上定出 各整数标高点,这些整数标高点称为刻度。如图 14-4 示,已知直线 AB 的标高投影 a3.5b6.7, 求直线 AB 上的整数标高点,作图方法是在标高投影 a3.5b6.7 的一侧作五条任意等距与 a3.5b6.7 平行的平行直线,令最下一条为 3 个单位,令最上一条为 7 个单位,分别过 a3.5 和 b6.7 作 a3.5b6.7的垂线,在垂线上分别按其标高数字 3.5 和 6.7 定出 A、B 两点。连接 AB,AB 与各

1234H 01234 图14-3直线的实长及倾角 图14-4直线的整数高程点 平行线的交点IV、V、VⅥ即为直线上的整数标高点。再把它们返回到直线的标高投影 sb67上,即得直线上的各整数标高点的投影。如各平行线间距采用单位长度,还可以 同时求出直线AB的实长和直线对基准面H的a倾角。 3、直线的坡度和平距 如图143示,直线上任意两点之间的高度差和它们的水平距离(水平投影长度)之比 称为直线的坡度,用符号1表示。 i=盖=生=ga 上式表示两点间的水平距离为1个单位(m)时两点的高度差即等于坡度。 当两点间的高度差为1个单位(m)时两点间的水平距离称为平距,用符号1表示。 1=*整=片=cga 由此可见,平距是坡度的倒数,坡度大则平距小,坡度小则平距大。 例1求图14-5所示直线AB的坡度与平距,并定出该直线上标高为4.3的C点。 解: 应先求出直线段AB的高差和水平距离H、L,然后利用上述公式确定直线的坡度 与平距。 H=7.3-3.3=4 L=8(注:按比例尺在图上量取得到) i=4== 1==2 HAc=7.3-4.3=3 LAC=HAc+i=6
α α Ⅳ Ⅴ Ⅵ α 图 14-3 直线的实长及倾角 图 14-4 直线的整数高程点 平行线的交点 IV、V、VI 即为直线上的整数标高点。再把它们返回到直线的标高投影 a3.5b6.7 上,即得直线上的各整数标高点的投影。如各平行线间距采用单位长度,还可以 同时求出直线 AB 的实长和直线对基准面 H 的 倾角。 3、直线的坡度和平距 如图 14-3 示,直线上任意两点之间的高度差和它们的水平距离(水平投影长度)之比 称为直线的坡度,用符号 i 表示。 i L tg H 水平距离 高度差 上式表示两点间的水平距离为 1 个单位(m)时两点的高度差即等于坡度。 当两点间的高度差为 1 个单位(m)时两点间的水平距离称为平距,用符号 l 表示。 l H ctg L 高度差 水平距离 由此可见,平距是坡度的倒数,坡度大则平距小,坡度小则平距大。 例 1 求图 14-5 所示直线 AB 的坡度与平距,并定出该直线上标高为 4.3 的 C 点。 解: 应先求出直线段 AB 的高差和水平距离 H、L,然后利用上述公式确定直线的坡度 与平距。 H=7.3-3.3=4 L=8 (注:按比例尺在图上量取得到) 2 1 8 4 L H i 2 1 i l HAC=7.3-4.3=3 LAC= HAC÷i=6

在图上按比例尺量取LAC6即得C点。 b33 C43 33 米 073 6 073 01234 图14-5直线的坡度和平距 §14.2平面的标高投影 一、平面的等高线和坡度比例尺 1、等高线 平面上的水平线称为等高线,在实际应用中常取平面上整数标高的水平线为等高 线。并把平面与基准面(H面)的交线作为高程为零的等高线。 图14-6表示平面上等高线的标高投影。平面上的等高线具有以下特性: (1)等高线是直线: (2)等高线互相平行: (3)等高线平距相等 2、坡度比例尺 如图14-6(a)示,平面上与等高线垂直的直线称为最大坡度线(即第五章中对H 面的最大斜度线)。最大坡度线对基准面H的倾角,即表示平面对基准面面的倾角。 最大坡度线的坡度就代表平面的坡度。 将平面P上的最大坡度线的投影附以整数高程,并画成一粗一细的双线,标注为 P1,使与一般直线有所区别,这种表示法称为平面的坡度比例尺,如图14-6(b)示。 根据画法几何中直角投影定理,标高投影中平面上的坡度比例尺与等高线垂直。坡度比 例尺上的刻度间距就是等高线的平距。 二、平面的常用表示法
在图上按比例尺量取 LAC=6 即得 C 点。 图 14-5 直线的坡度和平距 §14. 2 平面的标高投影 一、平面的等高线和坡度比例尺 1、等高线 平面上的水平线称为等高线,在实际应用中常取平面上整数标高的水平线为等高 线。并把平面与基准面(H 面)的交线作为高程为零的等高线。 图 14-6 表示平面上等高线的标高投影。平面上的等高线具有以下特性: (1)等高线是直线; (2)等高线互相平行; (3)等高线平距相等。 2、坡度比例尺 如图 14-6(a)示,平面上与等高线垂直的直线称为最大坡度线(即第五章中对 H 面的最大斜度线)。最大坡度线对基准面 H 的倾角,即表示平面对基准面面的倾角 。 最大坡度线的坡度就代表平面的坡度。 将平面 P 上的最大坡度线的投影附以整数高程,并画成一粗一细的双线,标注为 Pi,使与一般直线有所区别,这种表示法称为平面的坡度比例尺,如图 14-6(b)示。 根据画法几何中直角投影定理,标高投影中平面上的坡度比例尺与等高线垂直。坡度比 例尺上的刻度间距就是等高线的平距。 二、平面的常用表示法
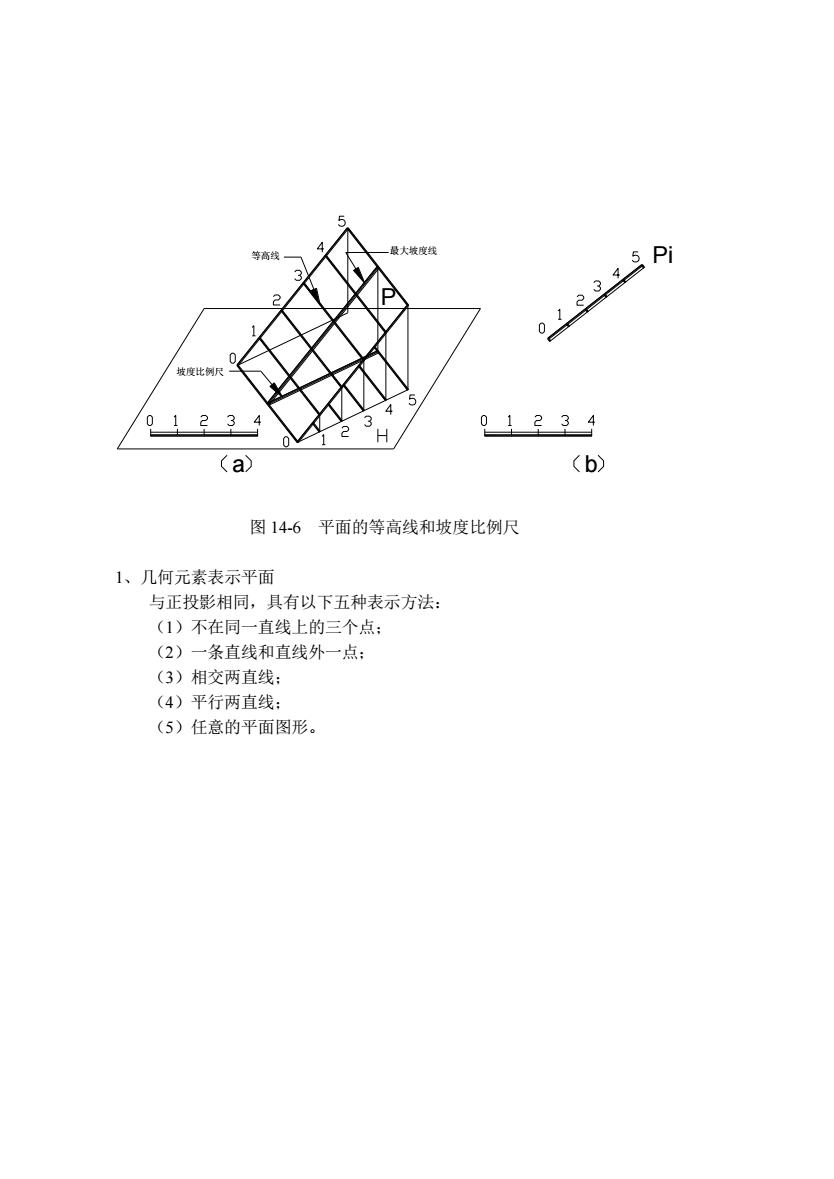
大装度线 1234 01234 (a) (b 图14-6平面的等高线和坡度比例尺 1、几何元素表示平面 与正投影相同,具有以下五种表示方法 (1)不在同一直线上的三个点: (2)一条直线和直线外一点: (3)相交两直线: (4)平行两直线: (5)任意的平面客图形
坡度比例尺 最大坡度线 等高线 a b P Pi 图 14-6 平面的等高线和坡度比例尺 1、几何元素表示平面 与正投影相同,具有以下五种表示方法: (1)不在同一直线上的三个点; (2)一条直线和直线外一点; (3)相交两直线; (4)平行两直线; (5)任意的平面图形

01234 图14-7坡度比例尺和等高线表示平面 2、坡度比例尺表示平面 如图147示,根据平面上的坡度比例尺与等高线垂直的关系,在标高投影中平面 的坡度比例尺的位置和方向一旦确定,平面的位置和方向随之而定,平面上的等高线也 相应确定。 3、一条等高线和平面的坡度表示平面 根据平面上的一条等高线可以确定平面的最大坡度线的方向,即平面的方向。由于 平面的坡度已知,则平面的位置和方向就确定了。如要求平面上的等高线,先利用坡度 得等高线的平距,然后作已知等高线的垂线,按图中比例在垂线上截取平距,过这些点 作已知等高线的平行线即为所求等高线,如图147示, 4、一条非等高线和平面的坡度表示平面 过一条直线可以作无数个平面,然而在平面的坡度和倾斜方向确定后,包含该直线 的平面就唯一确定。如图14-8()示,图中的箭头只是表示平面大致向直线的某一侧 倾斜,并不表示平面的准确坡度方向,因此将它画成带箭头的虚线
图 14-7 坡度比例尺和等高线表示平面 2、坡度比例尺表示平面 如图 14-7 示,根据平面上的坡度比例尺与等高线垂直的关系,在标高投影中平面 的坡度比例尺的位置和方向一旦确定,平面的位置和方向随之而定,平面上的等高线也 相应确定。 3、一条等高线和平面的坡度表示平面 根据平面上的一条等高线可以确定平面的最大坡度线的方向,即平面的方向。由于 平面的坡度已知,则平面的位置和方向就确定了。如要求平面上的等高线,先利用坡度 得等高线的平距,然后作已知等高线的垂线,按图中比例在垂线上截取平距,过这些点 作已知等高线的平行线即为所求等高线,如图 14-7 示, 4、一条非等高线和平面的坡度表示平面 过一条直线可以作无数个平面,然而在平面的坡度和倾斜方向确定后,包含该直线 的平面就唯一确定。如图 14-8(a)示,图中的箭头只是表示平面大致向直线的某一侧 倾斜,并不表示平面的准确坡度方向,因此将它画成带箭头的虚线
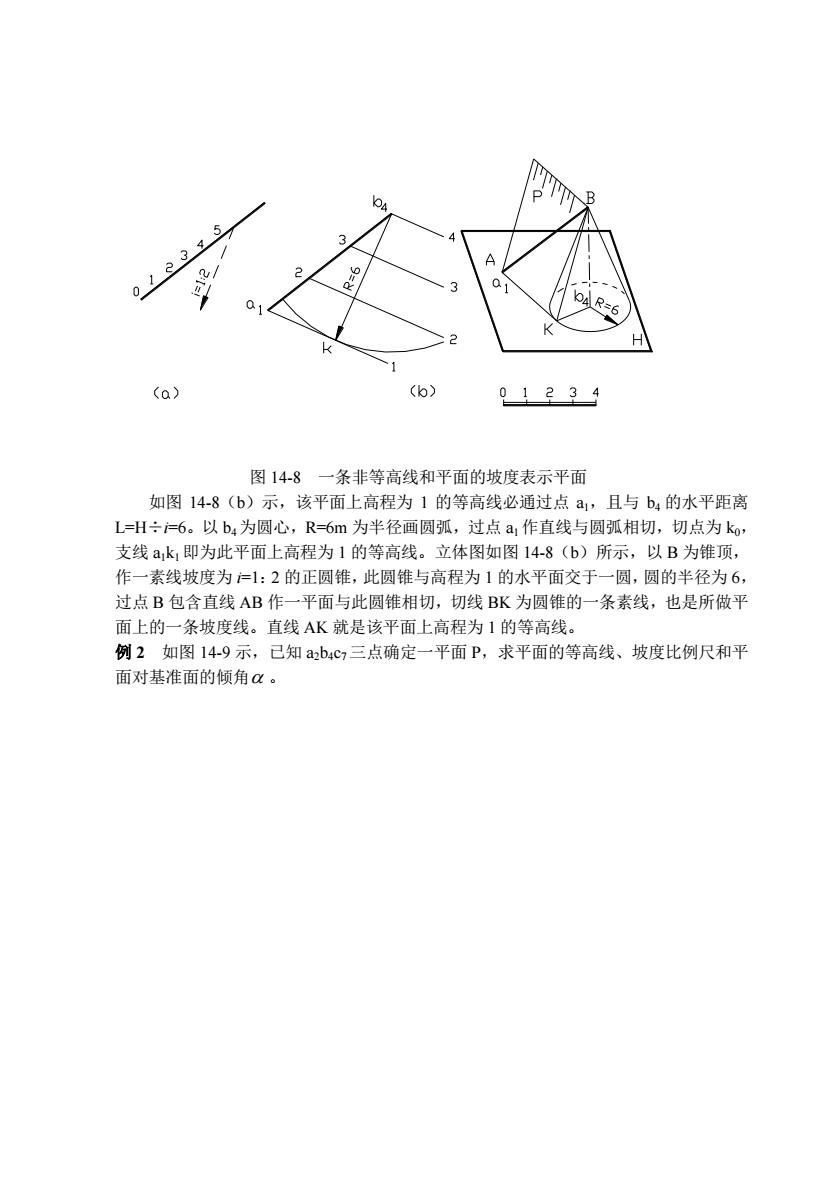
(6) 01234 图14-8一条非等高线和平面的坡度表示平面 如图14-8(b)示,该平面上高程为1的等高线必通过点a,且与b:的水平距离 L=H÷6。以b4为圆心,R=6m为半径画圆弧,过点a,作直线与圆弧相切,切点为ko, 支线k即为此平面上高程为1的等高线。立体图如图14-8(b)所示,以B为锥顶, 作一素线坡度为户1:2的正圆锥,此圆锥与高程为1的水平面交于一圆,圆的半径为6, 过点B包含直线AB作一平面与此圆锥相切,切线BK为圆锥的一条素线,也是所做平 面上的一条坡度线。直线AK就是该平面上高程为1的等高线。 例2如图149示,已知2bc三点确定一平面P,求平面的等高线、坡度比例尺和平 面对基准面的倾角α
图 14-8 一条非等高线和平面的坡度表示平面 如图 14-8(b)示,该平面上高程为 1 的等高线必通过点 a1,且与 b4 的水平距离 L=H÷i=6。以 b4为圆心,R=6m 为半径画圆弧,过点 a1作直线与圆弧相切,切点为 k0, 支线 a1k1 即为此平面上高程为 1 的等高线。立体图如图 14-8(b)所示,以 B 为锥顶, 作一素线坡度为 i=1:2 的正圆锥,此圆锥与高程为 1 的水平面交于一圆,圆的半径为 6, 过点 B 包含直线 AB 作一平面与此圆锥相切,切线 BK 为圆锥的一条素线,也是所做平 面上的一条坡度线。直线 AK 就是该平面上高程为 1 的等高线。 例 2 如图 14-9 示,已知 a2b4c7 三点确定一平面 P,求平面的等高线、坡度比例尺和平 面对基准面的倾角
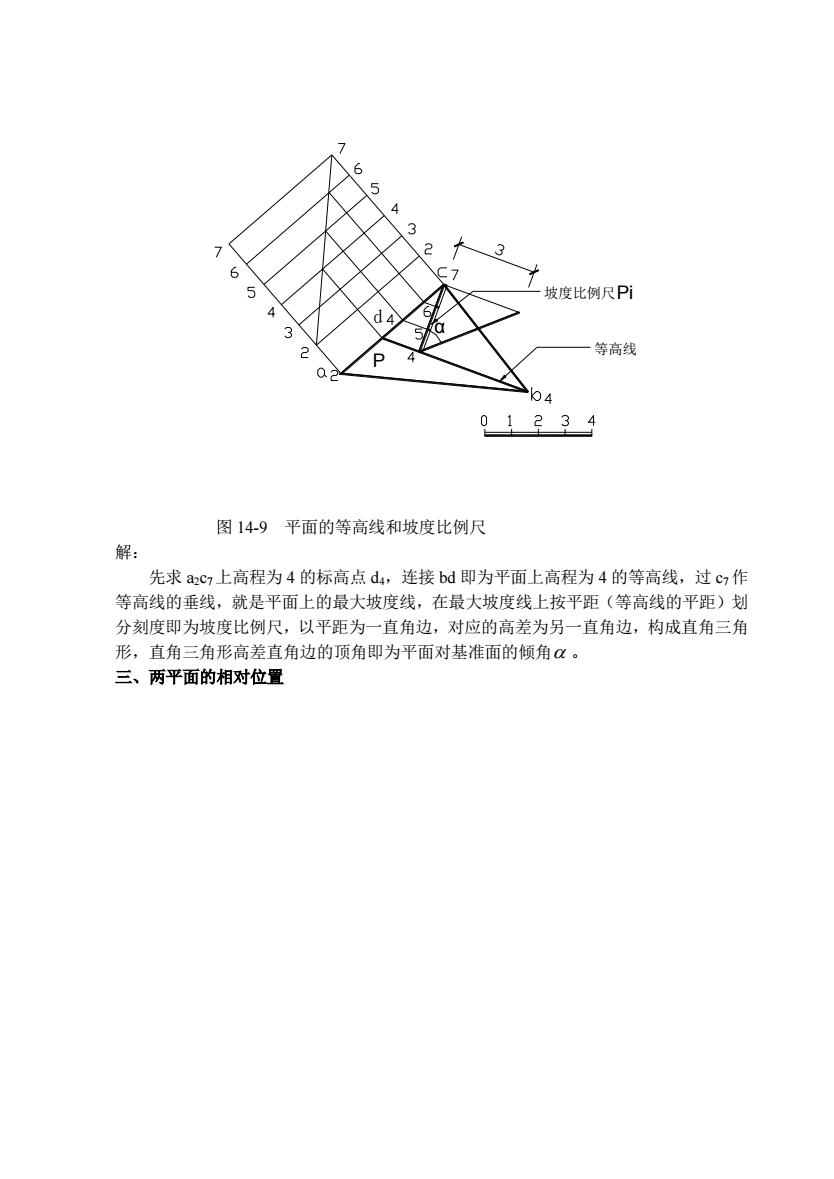
坡度比例尺Pj 等高线 01234 图14-9平面的等高线和坡度比例尺 解: 先求ac上高程为4的标高点d4,连接bd即为平面上高程为4的等高线,过c作 等高线的垂线,就是平面上的最大坡度线,在最大坡度线上按平距(等高线的平距)划 分刻度即为坡度比例尺,以平距为一直角边,对应的高差为另一直角边,构成直角三角 形,直角三角形高差直角边的顶角即为平面对基准面的倾角。 三、两平面的相对位置
α 等高线 坡度比例尺 d Pi P 图 14-9 平面的等高线和坡度比例尺 解: 先求 a2c7 上高程为 4 的标高点 d4,连接 bd 即为平面上高程为 4 的等高线,过 c7 作 等高线的垂线,就是平面上的最大坡度线,在最大坡度线上按平距(等高线的平距)划 分刻度即为坡度比例尺,以平距为一直角边,对应的高差为另一直角边,构成直角三角 形,直角三角形高差直角边的顶角即为平面对基准面的倾角 。 三、两平面的相对位置
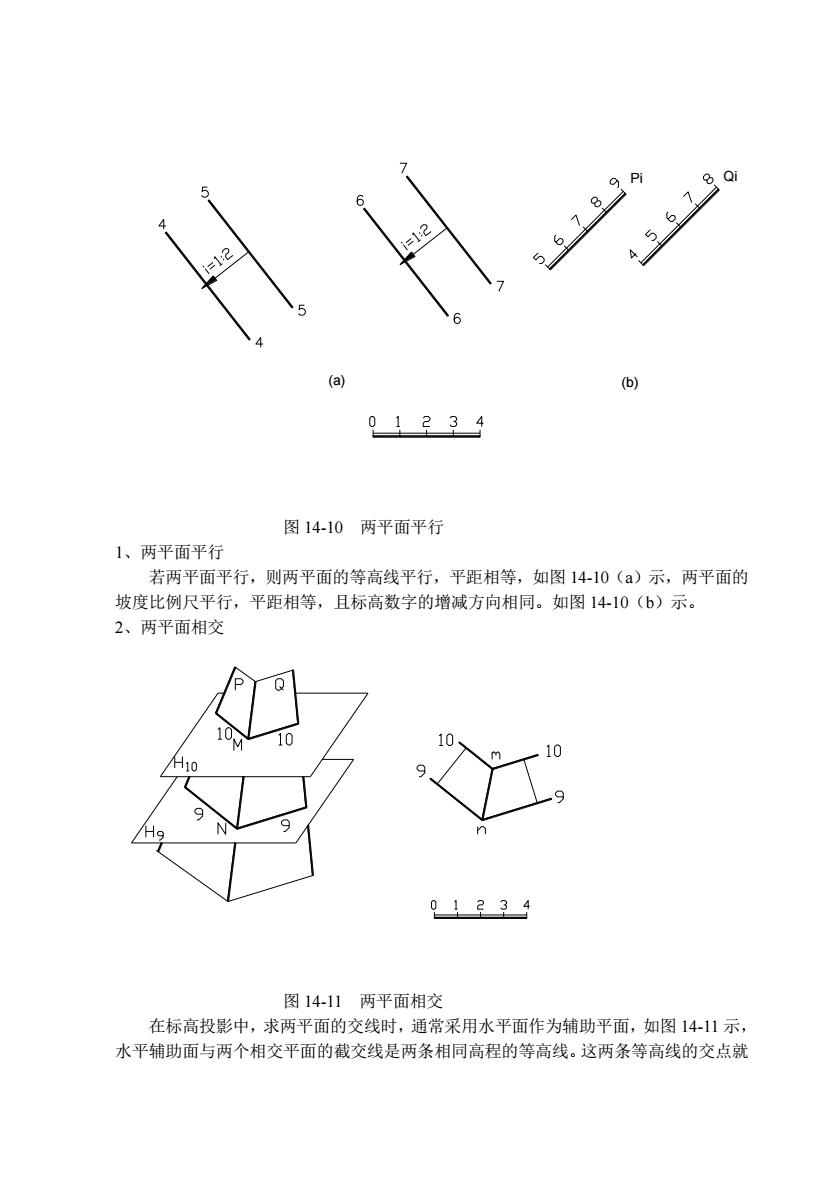
=12 12 56789 456 (a) 01234 图14-10两平面平行 1、两平面平行 若两平面平行,则两平面的等高线平行,平距相等,如图14-10()示,两平面的 坡度比例尺平行,平距相等,且标高数字的增减方向相同。如图14-10(b)示。 2、两平面相 Q 10 10 01239 图14-11两平面相交 在标高投影中,求两平面的交线时,通常采用水平面作为辅助平面,如图1411示 水平辅助面与两个相交平面的截交线是两条相同高程的等高线。这两条等高线的交点就
Pi Qi (a) (b) 图 14-10 两平面平行 1、两平面平行 若两平面平行,则两平面的等高线平行,平距相等,如图 14-10(a)示,两平面的 坡度比例尺平行,平距相等,且标高数字的增减方向相同。如图 14-10(b)示。 2、两平面相交 图 14-11 两平面相交 在标高投影中,求两平面的交线时,通常采用水平面作为辅助平面,如图 14-11 示, 水平辅助面与两个相交平面的截交线是两条相同高程的等高线。这两条等高线的交点就

是两平面的共有点,即交线上的点,重复上述过程,求得两个不同高程的等高线的交点, 连线即为两平面的交线。 =12 -2 dlll 01234 图14-12场地开挖线和坡面交线 实际工程中,把建筑物上相邻两坡面的交线称为坡面交线,坡面与地面的交线称为 坡脚线(填方)或开挖线(挖方)。 例3在高程为零的地面上挖一基坑,基坑底高程为一2m,基坑底的大小、形状和各坡 面的坡度如图1412示,求开挖线和坡面交线。 解: 开挖线:地面高程为零,因此开挖线就是个坡面上高程为零的等高线。它们分别与相应 的基坑底边线平行,其水平距离由L=H÷i求得, L1=L2=2÷1=2 L3=2÷(1/2)=4L4=2÷(1/1.5)=3 坡面交线:相邻两坡面上高程相同的两等高线的交点就是两坡面的共有点,分别连接相 应的两个共有点,即得到四条坡面交线。 示坡线:在高处等高线上用一系列长短线表示2面倾斜方向,这些长短线称为示坡线 示坡线的方向规定与面上的等高线垂直,长线一端指向下坡方向,即与最大坡度线方向 一致
是两平面的共有点,即交线上的点,重复上述过程,求得两个不同高程的等高线的交点, 连线即为两平面的交线。 图 14-12 场地开挖线和坡面交线 实际工程中,把建筑物上相邻两坡面的交线称为坡面交线,坡面与地面的交线称为 坡脚线(填方)或开挖线(挖方)。 例 3 在高程为零的地面上挖一基坑,基坑底高程为-2m,基坑底的大小、形状和各坡 面的坡度如图 14-12 示,求开挖线和坡面交线。 解: 开挖线:地面高程为零,因此开挖线就是个坡面上高程为零的等高线。它们分别与相应 的基坑底边线平行,其水平距离由 L=H÷i 求得, L1=L2=2÷1=2 L3=2÷(1/2)=4 L4=2÷(1/1.5)=3 坡面交线:相邻两坡面上高程相同的两等高线的交点就是两坡面的共有点,分别连接相 应的两个共有点,即得到四条坡面交线。 示坡线:在高处等高线上用一系列长短线表示 2 面倾斜方向,这些长短线称为示坡线, 示坡线的方向规定与面上的等高线垂直,长线一端指向下坡方向,即与最大坡度线方向 一致