第9章基本形体
第9章 基本形体 第3章

本章要求 1.掌握基本形体的投影特点及表面取点法; 2.掌握平面立体和曲面立体截交线的求法; 3掌握平平、平-曲、曲-曲相贯线的求法
本 章 要 求 1.掌握基本形体的投影特点及表面取点法; 2.掌握平面立体和曲面立体截交线的求法; 3.掌握平-平、平-曲、曲-曲相贯线的求法 。 本章要求 本章要 求

9.1基本形体的投影 >平面立体(棱柱、棱锥)的投影及 表面取点 >曲面立体(圆柱、圆锥、球、圆环) 的投影及表面取点
9.1 基本形体的投影 ➢平面立体(棱柱、棱锥)的投影及 表面取点 ➢曲面立体(圆柱、圆锥、球、圆环) 的投影及表面取点

常见的基本体 平面基本体 曲面基本体
基本体 常见的基本体 平面基本体 曲面基本体

9.1.1平面立体的投影及其表面取点 棱柱 (1)棱柱的组成 由两个底面和若干侧 棱面组成。棱线相互平行。 (2)棱柱的三视图 在图示位置时,正六棱柱 的顶面及底面为水平面,其水 平投影反映实形;前后棱面是 正平面,其正面投影反映实形; 其余四个棱面是铅垂面,它们 的水平投影都积聚成直线,与 正六边形的边重合
平面立体 在图示位置时,正六棱柱 的顶面及底面为水平面,其水 平投影反映实形;前后棱面是 正平面,其正面投影反映实形; 其余四个棱面是铅垂面,它们 的水平投影都积聚成直线,与 正六边形的边重合。 ⑵ 棱柱的三视图 ⑴ 棱柱的组成 由两个底面和若干侧 棱面组成。棱线相互平行。 棱柱 9.1.1平面立体的投影及其表面取点 V W H
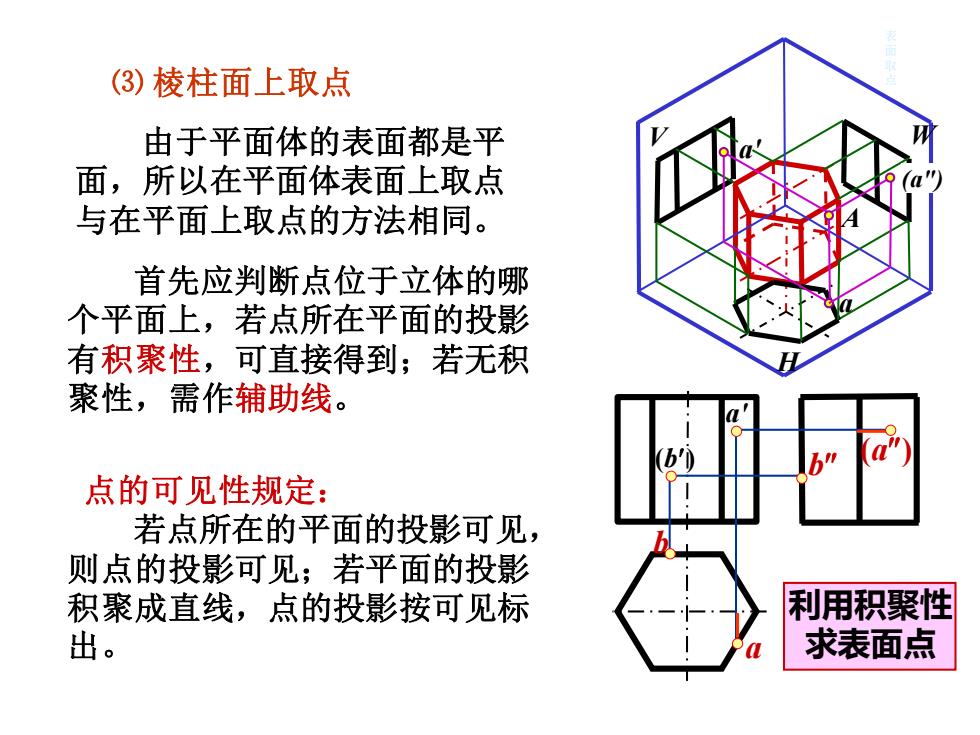
(3)棱柱面上取点 由于平面体的表面都是平 面,所以在平面体表面上取点 与在平面上取点的方法相同。 首先应判断点位于立体的哪 个平面上,若点所在平面的投影 有积聚性,可直接得到;若无积 聚性,需作辅助线。 b' 点的可见性规定: 若点所在的平面的投影可见, 则点的投影可见;若平面的投影 积聚成直线,点的投影按可见标 利用积聚性 出。 求表面点
由于平面体的表面都是平 面,所以在平面体表面上取点 与在平面上取点的方法相同。 点的可见性规定: 若点所在的平面的投影可见, 则点的投影可见;若平面的投影 积聚成直线,点的投影按可见标 出。 ⑶ 棱柱面上取点 首先应判断点位于立体的哪 个平面上,若点所在平面的投影 有积聚性,可直接得到;若无积 聚性,需作辅助线。 V W H 表 面 取 点 a' a (a") A 利用积聚性 求表面点 (b) a' a b b (a)
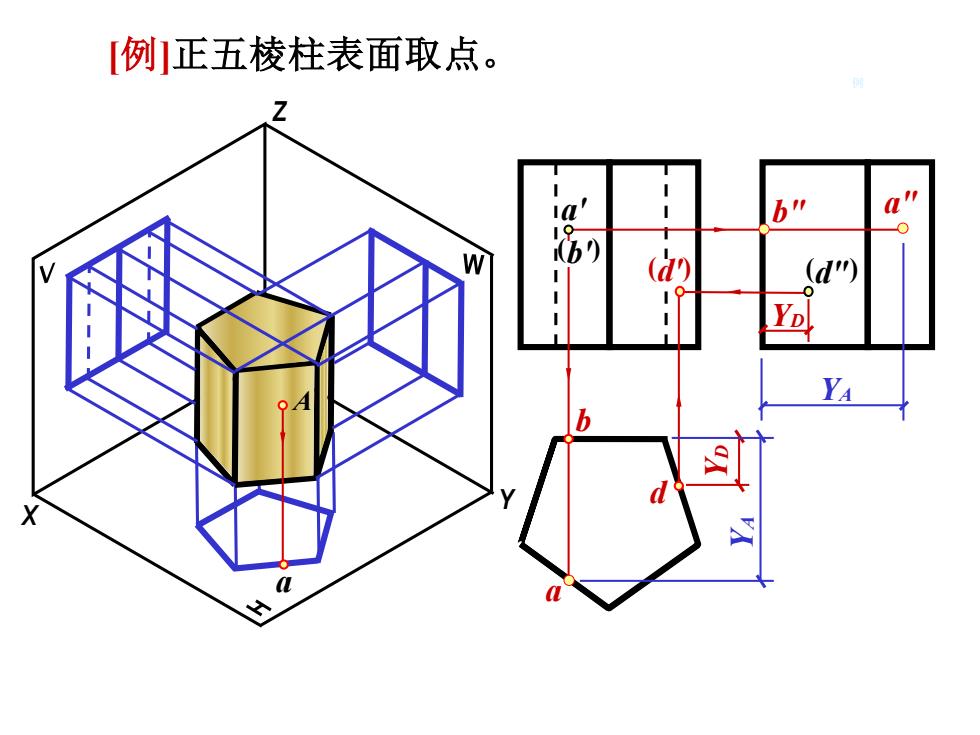
[例]正五棱柱表面取点。 ia' b" (d0 (d") Ya X H Z
a [例]正五棱柱表面取点。 X Y Z O a' (d") b (d') d A 例 b" a" (b') a YD YD YA YA
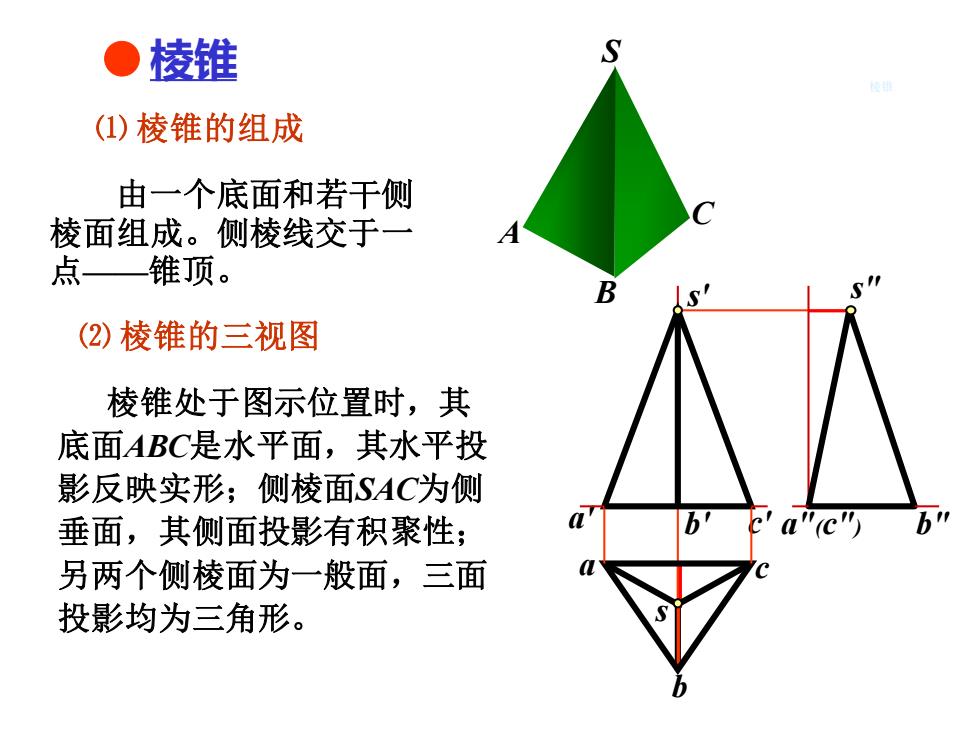
● 棱推 S (1)棱锥的组成 由一个底面和若干侧 棱面组成。侧棱线交于一 点—锥顶。 (2)棱锥的三视图 棱锥处于图示位置时,其 底面ABC是水平面,其水平投 影反映实形;侧棱面SAC为侧 垂面,其侧面投影有积聚性; "ic") 另两个侧棱面为一般面,三面 投影均为三角形
a' c' 棱锥 棱锥 ⑵ 棱锥的三视图 b' a b c a"(c") b" ⑴ 棱锥的组成 由一个底面和若干侧 棱面组成。侧棱线交于一 点——锥顶。 A B C S 棱锥处于图示位置时,其 底面ABC是水平面,其水平投 影反映实形;侧棱面SAC为侧 垂面,其侧面投影有积聚性; 另两个侧棱面为一般面,三面 投影均为三角形。 s s' s

(3)在棱锥面上取点 首先应判断点位于立体的哪个平面上,若点所在平面的投影 有积聚性,可直接得到;若点所在的表面投影没有积聚性,则需 在点所在的平面上作辅助线。 与已知点连线(BC) 作已知线平行线(MN)
m' n' m n a a' n" a" m" 与已知点连线(BC) 作已知线平行线(MN) ⑶ 在棱锥面上取点 首先应判断点位于立体的哪个平面上,若点所在平面的投影 有积聚性,可直接得到;若点所在的表面投影没有积聚性,则需 在点所在的平面上作辅助线。 c' b' c b c" b" a a' a" 表面取点
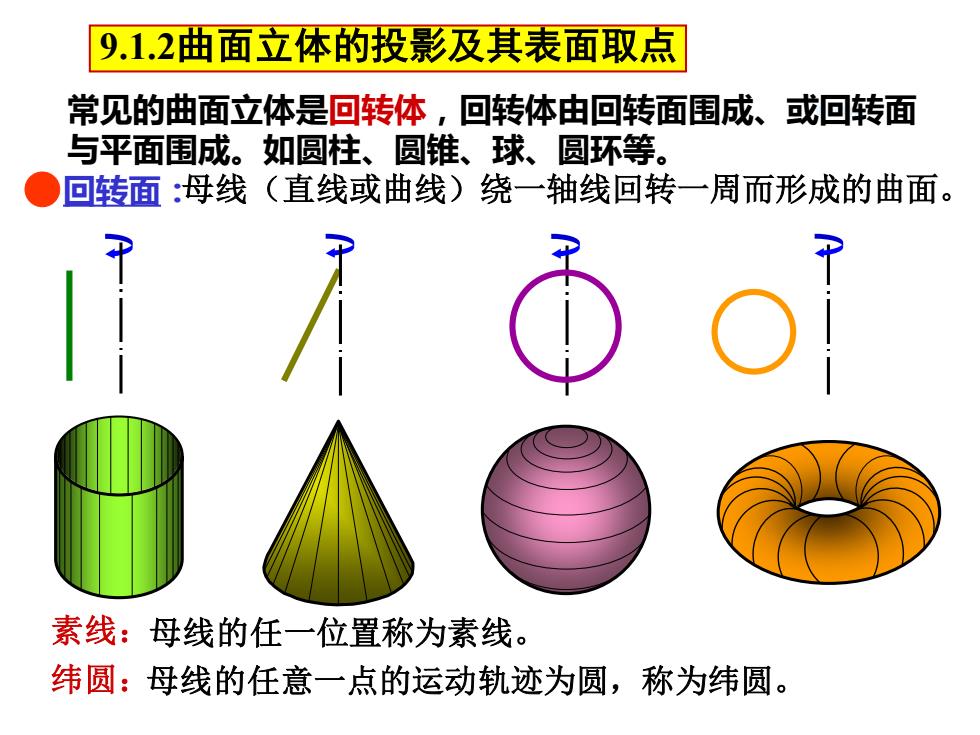
9.1.2曲面立体的投影及其表面取点 常见的曲面立体是回转体,回转体由回转面围成、或回转面 与平面围成。如圆柱、圆锥、球、圆环等。 ●回转面:母线(直线或曲线)绕一轴线回转一周而形成的曲面。 素线:母线的任一位置称为素线。 纬圆:母线的任意一点的运动轨迹为圆,称为纬圆
回转面:母线(直线或曲线)绕一轴线回转一周而形成的曲面。 素线:母线的任一位置称为素线。 纬圆:母线的任意一点的运动轨迹为圆,称为纬圆。 常见的曲面立体是回转体,回转体由回转面围成、或回转面 曲面立体 与平面围成。如圆柱、圆锥、球、圆环等。 9.1.2曲面立体的投影及其表面取点