
第五章平 面 第一节。平面的投影及其表示法 一、用几何元素表示平面 不属于同一直线上的三点可以确定一平面。根据几何原理也可以转换为:一点一直线:相 交两直线;平行两直线或任何 一平面图形来确定平面。因此,在投影图上可以用图51中任 组几何元素的投影表示平面。 长子令 图51几问元素表示的平面 如图5-2所示,在三投影体系中,平面对投影面的相对位置,可分为三类 (1)对三个投影面都倾斜的平面称为一般位置平面,如图示C面。 (2)垂直于一个投影面同时对其他两投影面倾斜的平面称为投影面垂直面,如图示B,D、 F面。 (3)平行于一个投影面的平面称为投影面平行面,如图示A,E,G面。 其中,后两类称为特殊位置平面。 二、各种位置平面的投影 下面分别介绍三类平面的投影特性。 1.一般位置平面 因一般位置平面同时倾斜于三个投影面,故它的三个投影均为类似图形。如图52中的 C面是梯形,故其三面投影均为梯形(图53)。 2.垂直于一个投影面的平面 垂直于一个投影面同时对其他两投影面倾斜的平面,统称为投影面垂直面。垂直于H面 的平面,称为铅垂面:垂直于V面的平面,称为正垂面:垂直于W面的平面,称为侧垂面。 如图5-4所示铅垂面F,垂直于H面,倾斜于V面和W面,故其水平投影积聚为一直线,V 面和甲面投影为类似图形:铅垂面的水平投影与OX轴的交角,反映该平面对V面的角度B: 铅垂面的水平投影与OY轴的交角,反映该平面对W面的角度y。 .35
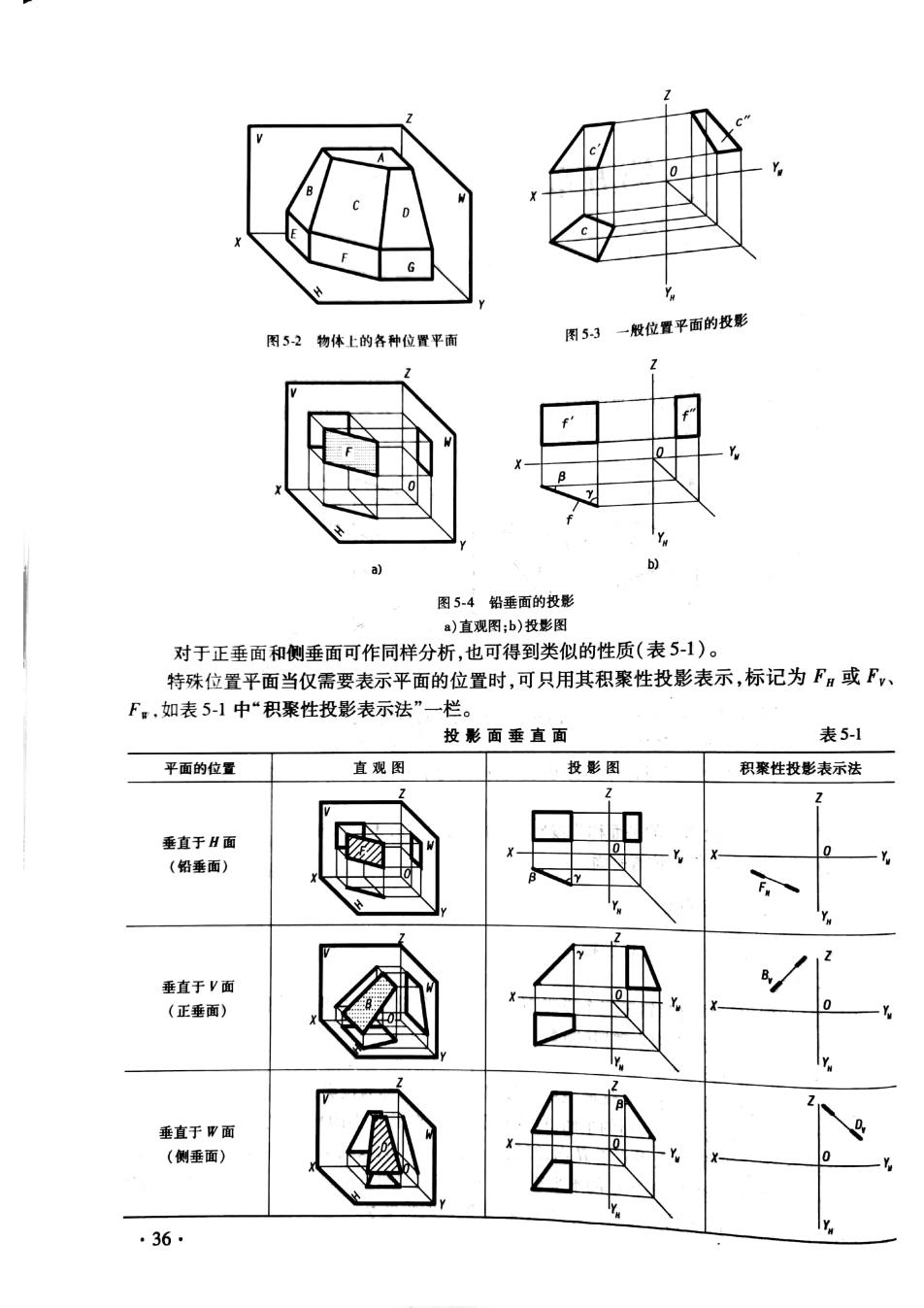
图52物体上的各种位置平面 图53一般位置平面的投影 图5-4铅垂面的投影 }古迎图:b)投影图 对于正垂面和侧垂面可作同样分析,也可得到类似的性质(表51)。 特殊位置平面当仅需要表示平面的位置时,可只用其积聚性投影表示,标记为Fa或F,、 F,.如表5-1中“积聚性投影表示法”一栏 投形面垂直面 表5-1 平面的位置 直观图 投影图 积聚性投影表示法 垂直于H面 (铅垂面) 垂直于V面 (正垂面) 垂直于甲面 (侧垂面) ·36
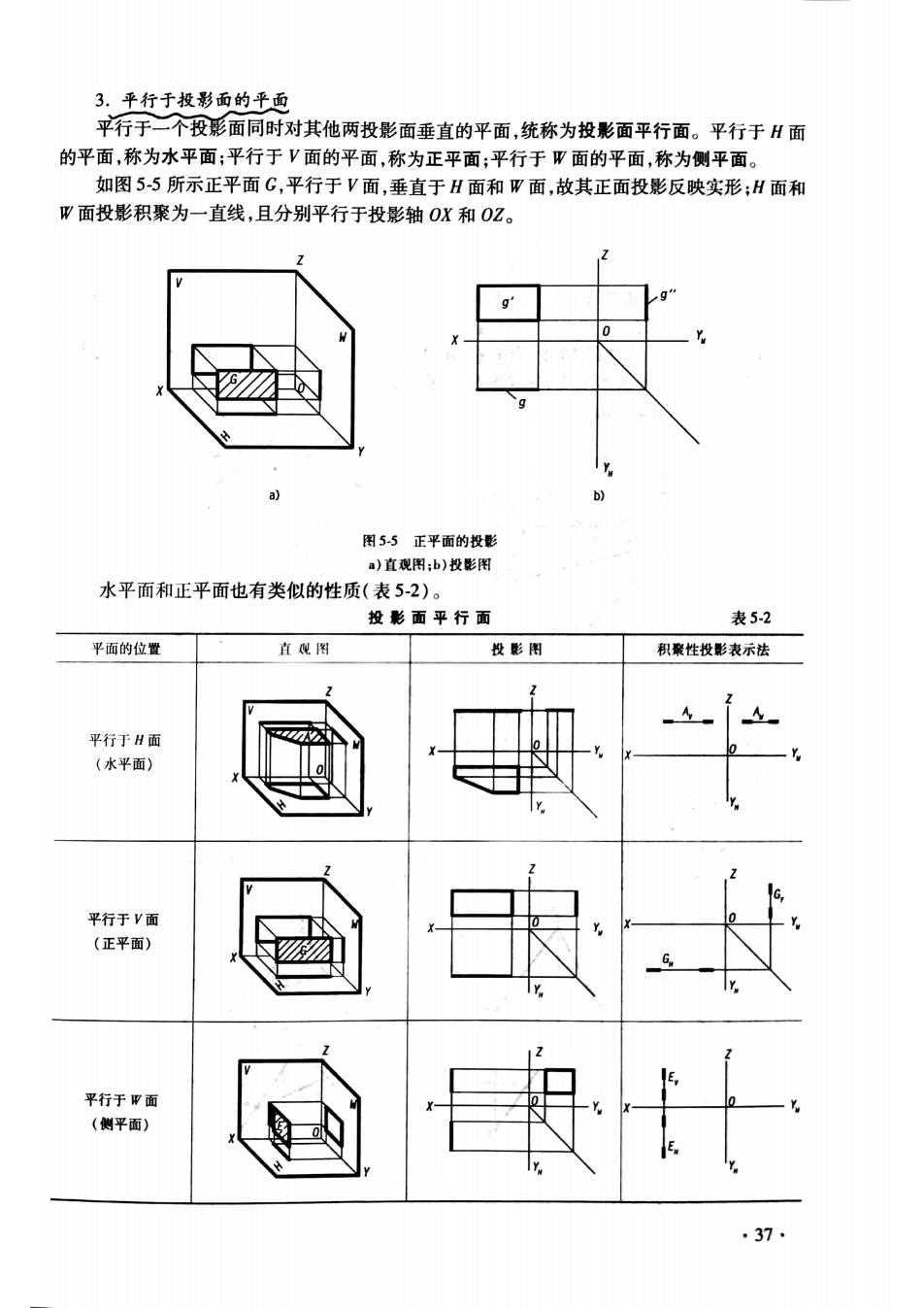
3.平行于投影面的平面 平行于一个投影面同时对其他两投影面垂直的平面,统称为投影面平行面。平行于H面 的平面,称为水平面;平行于V面的平面,称为正平面:平行于W面的平面,称为侧平面。 如图55所示正平面G,平行于V面,垂直于H面和W面,故其正面投影反映实形:H面和 W面投影积聚为一直线,且分别平行于投影轴OX和OZ。 图55正平面的投 a)直观用:b)投影图 水平面和正平面也有类似的性质(表5-2)。 投影面平行面 表5-2 平面的位置 直型图 投影图 积聚性投影表示法 平行于H面 (水平面) 平行于V面 (正平面) 农 平行于甲面 (侧平面) .37
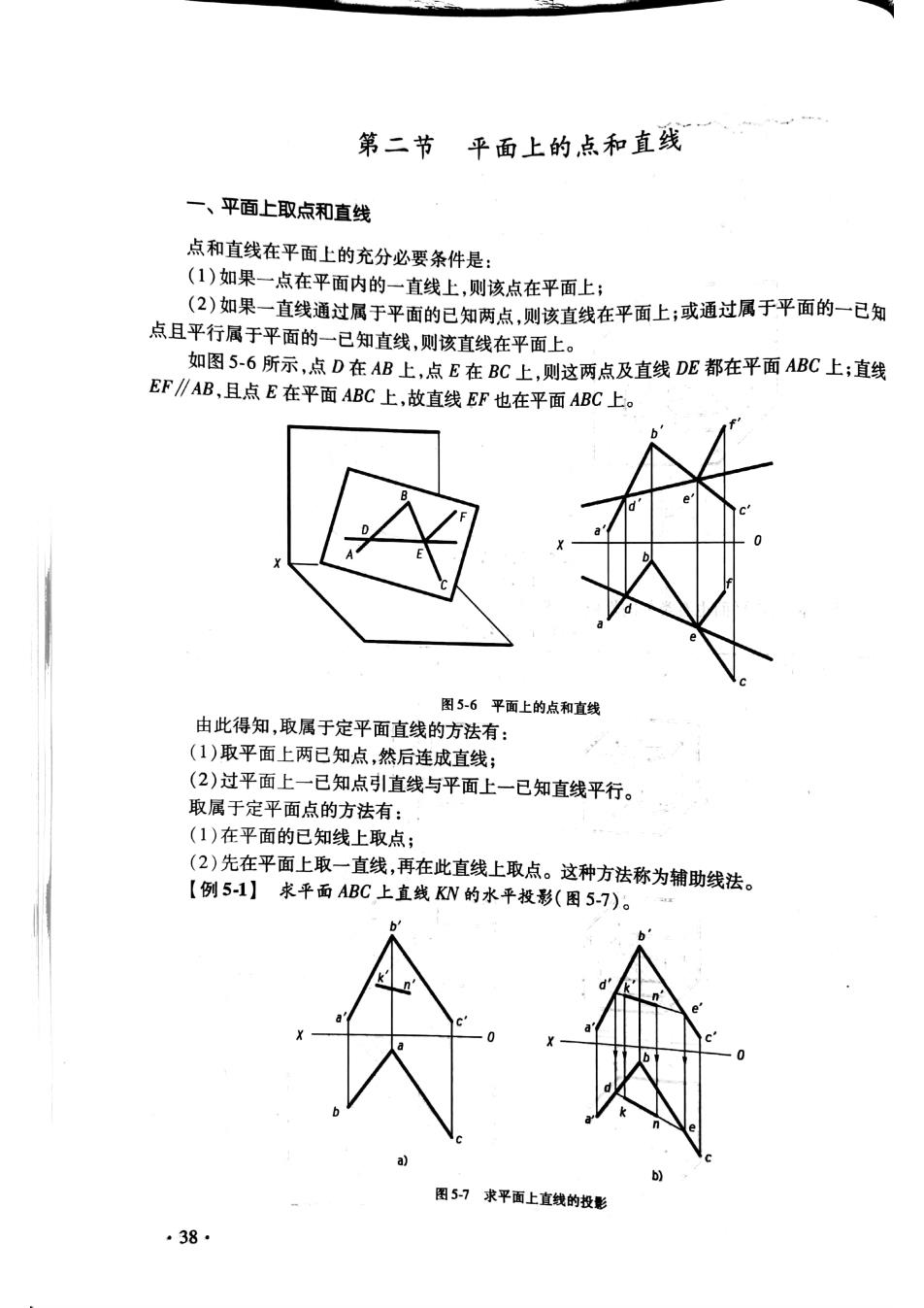
第二节平面上的点和直线“ 一、平面上取点和直线 点和直线在平面上的充分必要条件是; (1)如果一点在平面内的一直线上,则该点在平面上: (2)如果一直线通过属于平面的已知两点,则该直线在平面上;或通过属于平面的一已知 点且平行属于平面的一已知直线,则该直线在平面上。 如图5-6所示,点D在AB上,点E在BC上,则这两点及直线DB都在平面MBC上:直线 EF∥AB,且点E在平面ABC上,故直线EF也在平面ABC上。 图5-6平面上的点和直线 由此得知,取属于定平面直线的方法有: (1)取平面上两已知点,然后连成直线: (2)过平面上一已知点引直线与平面上一已知直线平行。 取属于定平面点的方法有: (1)在平面的已知线上取点; (2)先在平面上取一直线,再在此直线上取点。这种方法称为辅助线法。】 【例51】求平面ABC上直线KW的水平投影(围5-7)。 图5-7求平面上直线的投影 38
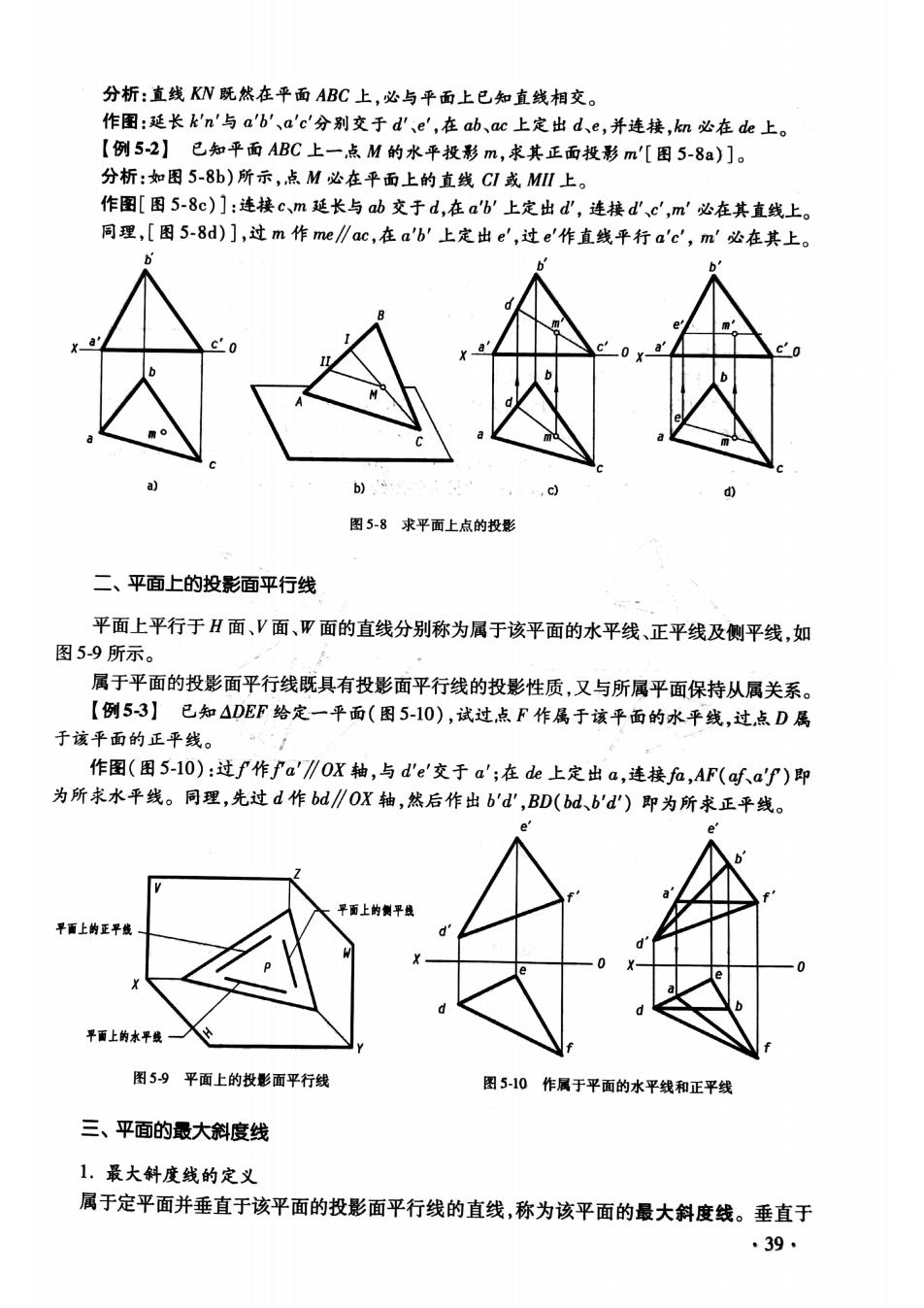
分析:直线KW既然在平面ABC上,必与平面上已知直线相交。 作图:延长k'n'与a'b'、a'c'分别交于d',e',在ab、ac上定出d、e,并连接,m必在de上。 【例52】已知平面ABC上一点M的水平投形m,求其正面投影m'[图5-8a)]。 分析:如图5-8b)所示,点M必在平面上的直线C1或M上。 作图[图5-8c)门:连接c、m延长与b交于d,在a'W上定出d,连接d'、c',m'必在其直线上 同理,[图5-8d)],过m作me∥ac,在a'b'上定出e',过e'作直线平行a'c',m'必在其上。 图5-8求平面上点的投影 二、平面上的投影面平行线 平面上平行于H面、V面、W面的直线分别称为属于该平面的水平线、正平线及侧平线,如 图5-9所示。 属于平面的投影面平行线既具有投影面平行线的投影性质,又与所属平面保持从属关系。 【例53】已知ADEF给定一平面(图5-10),试过点F作属于该平面的水平线,过点D属 于该平面的正平线。 作图(困5-10):过f作fa'∥0x轴,与d'e'交于a';在de上定出a,连接f,AF(afaf)即 为所求水平线。同理,先过d作bd∥OX轴,然后作出b'd',BD(bd、b'd')即为所求正平线。 图59平面上的投影面平行线 图5-10 作属于平面的水平线和正平线 三、平面的最大斜度线 1,最大斜度线的定义 属于定平面并垂直于该平面的投影面平行线的直线,称为该平面的最大斜度线。垂直于 ·39

水平线的直线称为对水平投影面的最大斜度线:垂直于正平线的直线,称为对正投影面的表 大斜度线:垂直于侧平线的直线,称为对侧投影面的最大斜度线。 如图5-11所示,直线CD是属于平面P的水平 线,垂直于CD且属于平面P的直线AF是对H面的 最大斜度线。 如图5-12所示,定平面44BC。为作该平面上对 水平投影面的最大斜度线,先任意引一水平线CD (cd,c'd'")。再根据直角投影定理在平面上任作CD 的垂线AF(af,a),AF即为该平面上对水平投影面 的最大斜度线。 2.最大斜度线对投影面的角度最大 图5-11最大斜度线 如图5-13所示,CD对H面的夹角为O°,最大斜度线对H面的夹角为α。过点A作最大斜 度线以外该平面上任意直线AB。它对H面的夹角为。因AF⊥CD,且BF∥CD,故AF1BP, 根据直角投影定理,aF⊥BF,则aB>aF,两个直角三角形Aba和Aa有相等的直角边Aa,而另 一对直角边aB>aF,相应的锐角w<a。故最大斜度线对投影面的角度最大。 图5-12对水平投影面的最大斜度线4 图513最大斜度线 ·40