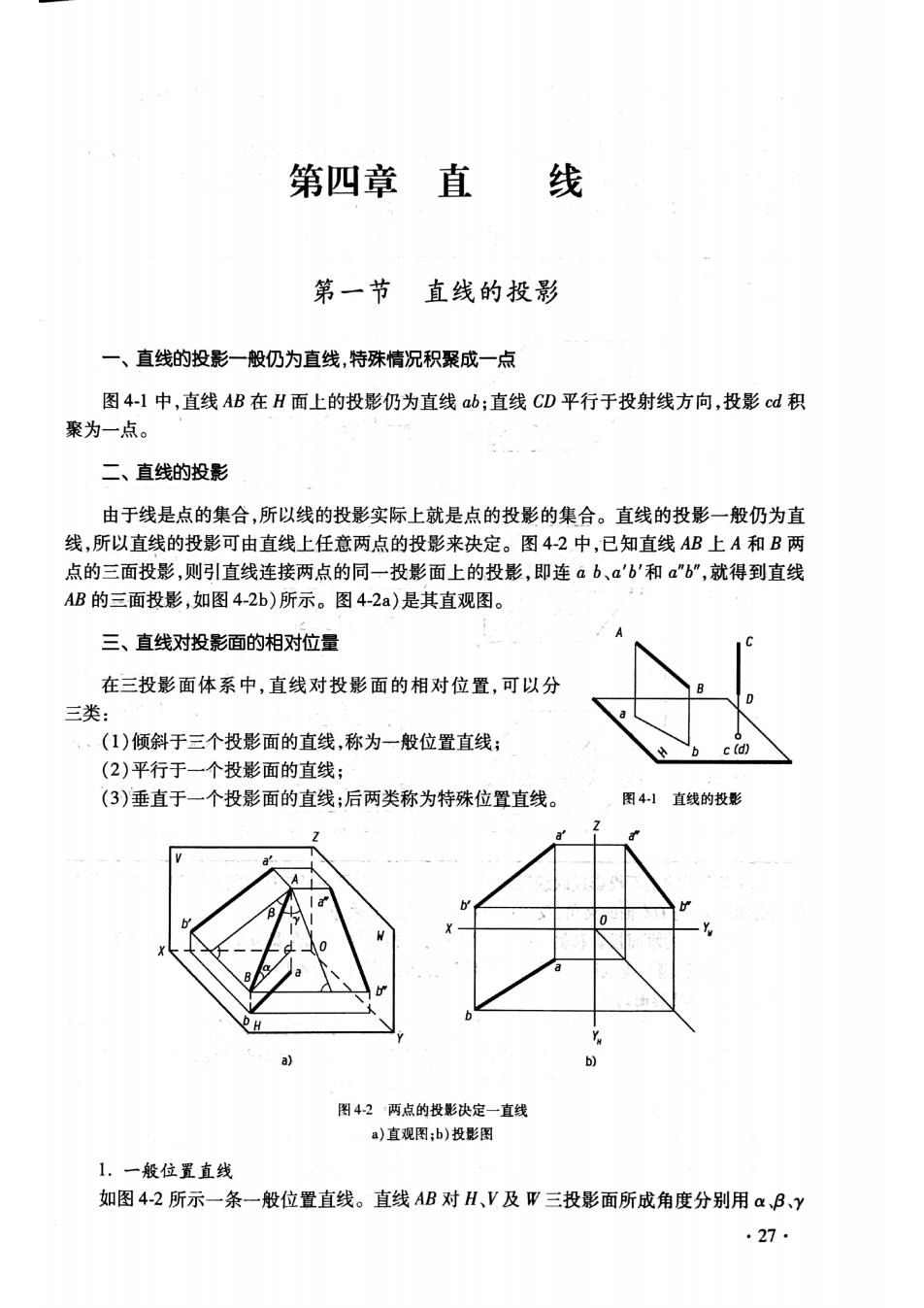
第四章直 线 第一节直线的投影 一、直线的投影一般仍为直线,特殊情况积聚成一点 图4-1中,直线AB在H面上的投影仍为直线ab;直线CD平行于投射线方向,投影cd积 聚为一点。 二、直线的投影 由于线是点的集合,所以线的投影实际上就是点的投影的集合。直线的投影一般仍为直 线,所以直线的投影可由直线上任意两点的投影来决定。图42中,已知直线AB上A和B两 点的三面投影,则引直线连接两点的同一投影面上的投影,即连ab、a'b'和a'b“,就得到直线 AB的三面投影,如图4-2b)所示。图4-2a)是其直观图。 三、直线对投影面的相对位量 在三投影面体系中,直线对投影面的相对位置,可以分 三类: (1)倾斜于三个投影面的直线,称为一般位置直线: (2)平行于一个投影面的直线; (3)垂直于一个投影面的直线;后两类称为特殊位置直线。 图41直线的投 图42两点的投影决定一直线 a)直观图:b)投影图 1.一般位置直线 如图4-2所示一条一般位置直线。直线AB对H、V及平三投影面所成角度分别用αB、y .27
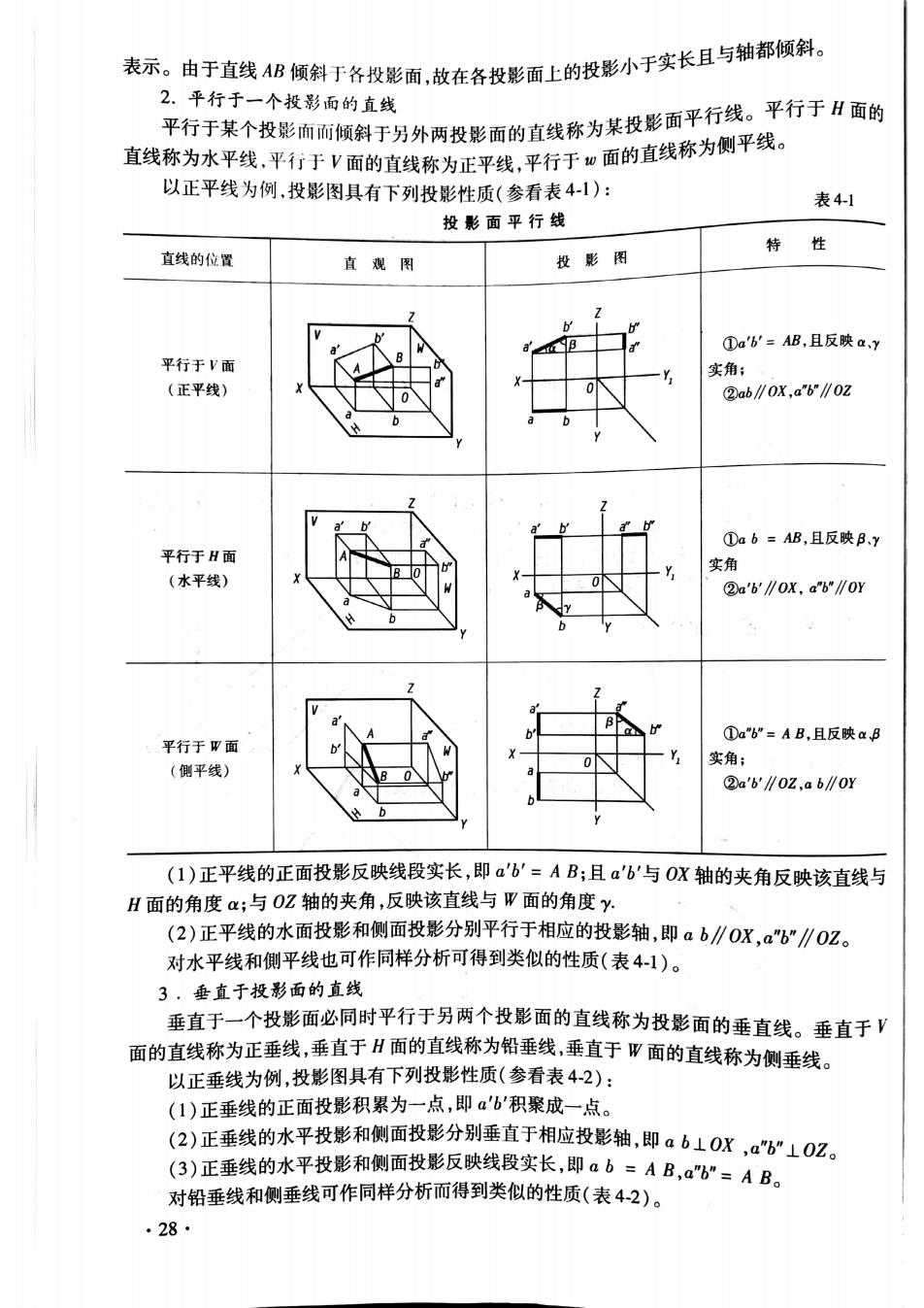
表示,由于直线仍倾斜于名投影面,放在各投影面上的投影小于实长且与轴都倾斜。 2.平行于一个投影面的直线 平行于某个投影南面顿斜于另外两投影面的直线称为某投影面平行线,平行于H面的 直线称为水平线,平行于V面的直线称为正平线:平行于。面的直线称为侧平线。 以正平线为例,投影图具有下列投影性质(参看表4): 表4-1 投影面平行线 特性 直线的位置 直观图 投影 ①ab=AB,且反映a,y 平行于V面 实角: (正平线) 0 ②ab∥0x,ab∥0z ①ab=AB,且反映By 平行于H面 实角 (水平线) ②aB'∥0x.ab"∥0Y ①a6"=AB,且反映aB 平行于W面 (侧平线) 实角 (1)正平线的正面投影反映线段实长,即a'6'=AB;且ab'与Ox轴的夹角反映该直线与 H面的角度a;与O2轴的夹角,反映该直线与W面的角度y. (2)正平线的水面投影和侧面投影分别平行于相应的投影轴,即ab∥OX,ab∥02。 对水平线和侧平线也可作同样分析可得到类似的性质(表41)。 3,垂直于投影面的直线 垂直于一个投影面必同时平行于另两个投影面的直线称为投影面的垂直线。垂直于V 面的直线称为正垂线,垂直于H而的直线称为铅垂线,垂直于甲面的直线称为侧垂线。 以正垂线为例,投影图具有下列投影性质(参看表4-2): (1)正垂线的正面投影积累为一点,即a'b'积聚成一点。 (2)正垂线的水平投影和侧面投影分别垂直于相应投影轴,即a610X,a6”102。 (3)正垂线的水平投影和侧面投影反映线段实长,即a6=AB,a。AB。 对铅垂线和侧垂线可作同样分析而得到类似的性质(表42)。 28
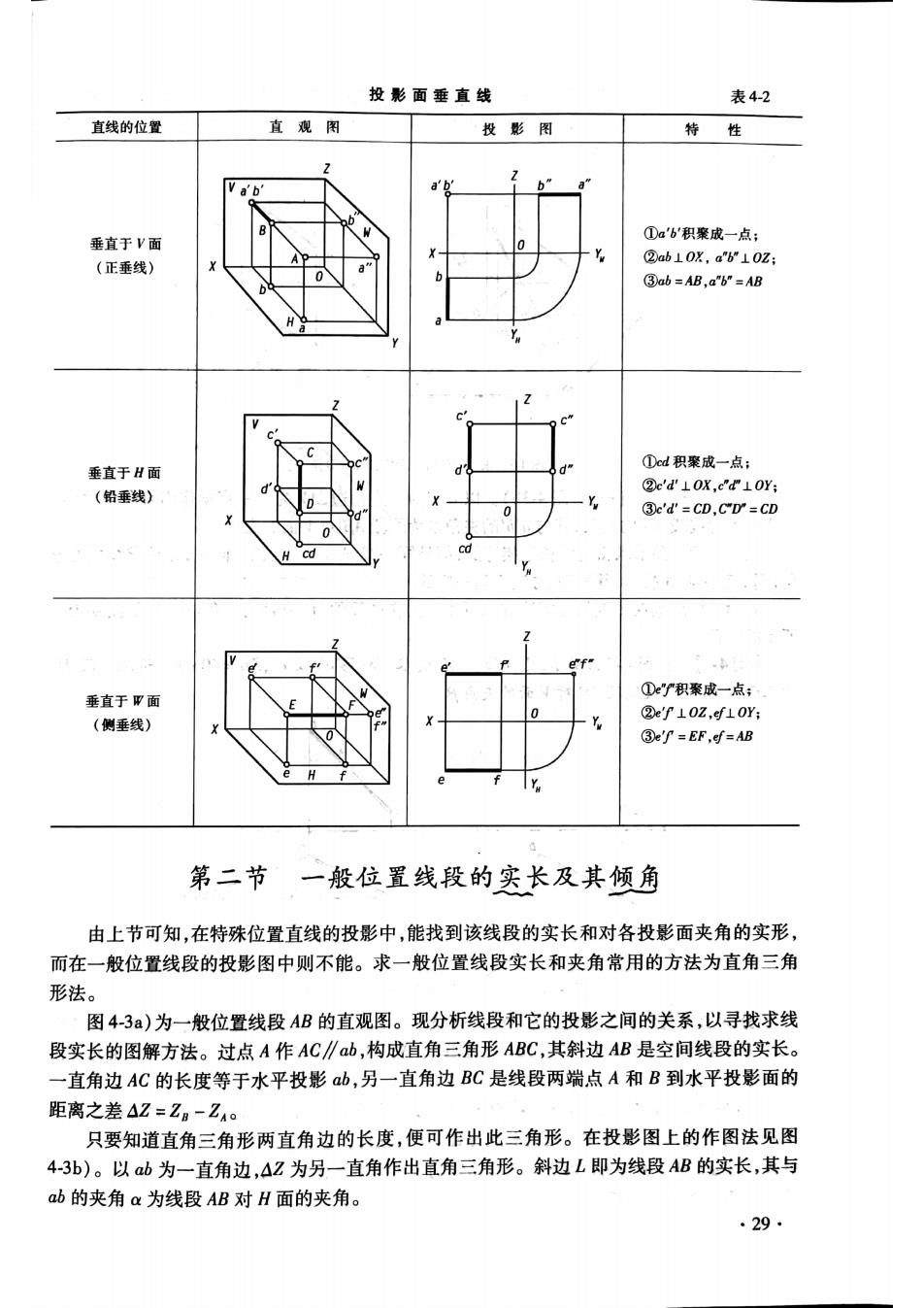
投影面垂直线 表4-2 直线的位置 直观图 投影图 特性 ①a'b积聚成一点: 垂直于V面 (正垂线) ②ab10以,a610z: ③ab=AB,ar=AB 垂直于H面 ①d积案成一点 (铅垂线) 'd'Lox,' ③c'd'=CD,Cr=CL 垂直于甲面 ①了积聚成一点; (侧垂线) ②eP⊥0Z,ef⊥OY: ③ef=EF,gf=AB 第二节 一般位置线段的实长及其倾角 由上节可知,在特殊位置直线的投影中,能找到该线段的实长和对各投影面夹角的实形, 而在一般位置线段的投影图中则不能。求一般位置线段实长和夹角常用的方法为直角三角 形法。 图4-3a)为一般位置线段AB的直观图。现分析线段和它的投影之间的关系,以寻找求线 段实长的图解方法。过点A作AC∥b,构成直角三角形ABC,其斜边AB是空间线段的实长 一直角边AC的长度等于水平投影ab,另一直角边BC是线段两端点A和B到水平投影面的 距离之差4Z=Zg-Z4。 只要知道直角三角形两直角边的长度,便可作出此三角形。在投影图上的作图法见图 4-3b)。以b为一直角边,A2为另一直角作出直角三角形。斜边L即为线段AB的实长,其与 ab的夹角a为线段AB对H面的夹角。 .29

如4所以过友B作Da?,枸底直角三角彩AB0。其斜边是客间线段酶 长直角边即的长度等于正国设能。构穷直算角边D是线段两装点A和日到正面 面的距离之差△Y=Y,-Y0 图43求一般位置线段实长和aB角 在投影图上的作图法见图43b)。以a'6'为一直角边,△Y为另一直角作出直角三角形 斜边L即为线段AB的实长,其与ab'的夹角B为线段AB对V面的夹角。 两个直角三角形求得的实长是相等的,都是同一线段AB的实长。同理,如欲求线段的, 角,则需利用侧面投影,其原理、方法都是一样的。 直角三角形画在图纸的任何地方都可以。为作图简便,可将直角三角形画在如图44b) 所示的位置。 【例4-1】如图4-4a)所示,已知线段AB的水平投影ab及a',AB=40mm。试求线段AB 的正面投影a'b',及线段AB对V面的夹角B。 图44求一般位置线段AB的正面投影'b和夹角B 分析B夫角所在的直角三角形中,一直角边为线段AB的正面投影'6,另一直角边是线 段两端点A和B到正面授面的距离之△Y=业-Y,斜边L为线段AB的实长。由此可作 出此直角三角形 解:知国44b)所示,过a作0轴的平行线构成直角,以6为圆心,L为丰径作孤交谊线 于点A,得直角三角形:一直角边的长度为△Y=-业,另一直角边的长度为正面投移0 斜边L与06的夹角为B。以@'为国心,a'的长度为丰径作孤交过b与om轴套直的线于6 连a'b'即为所求正面投影。 ,30
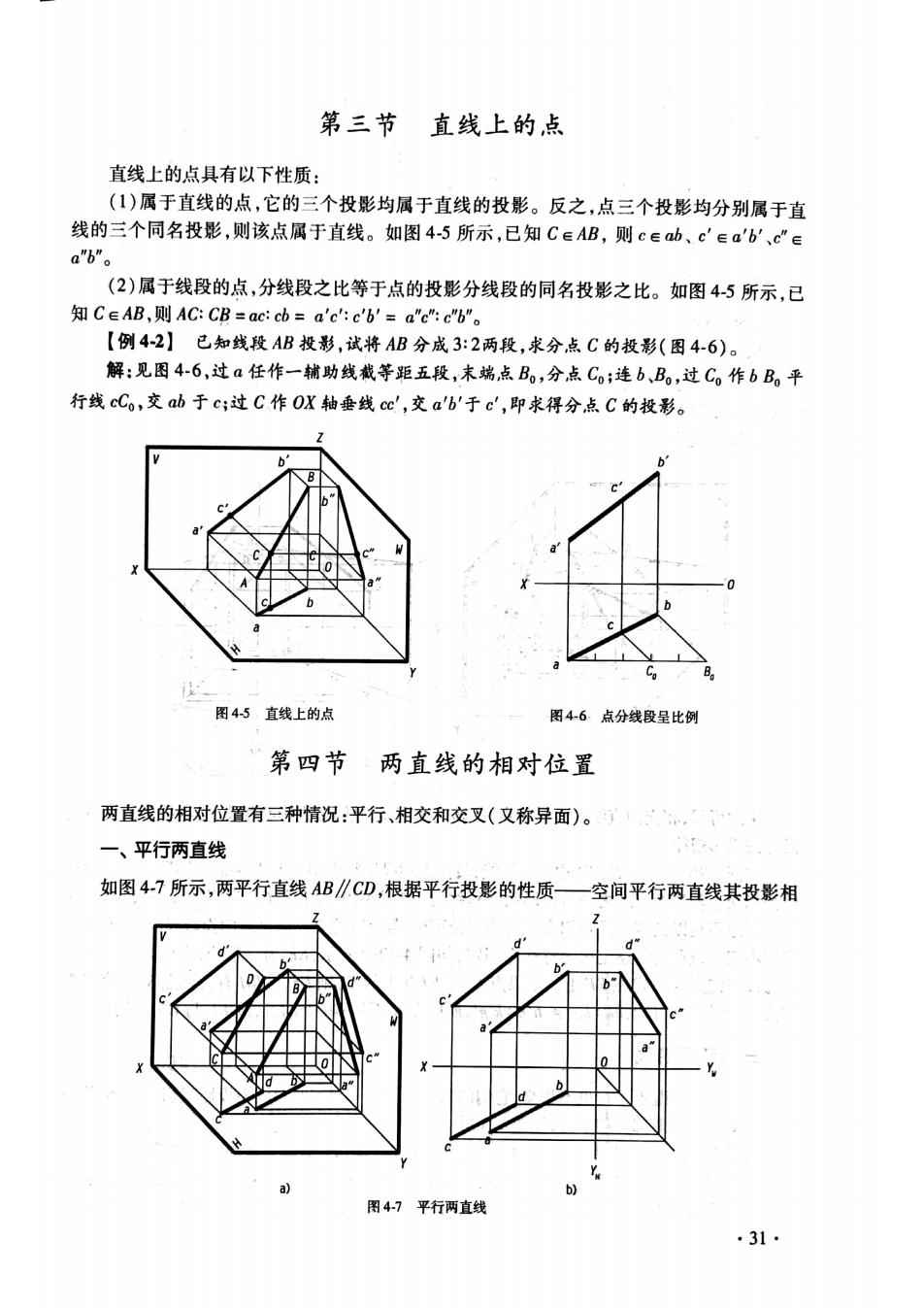
第三节直线上的点 直线上的点具有以下性质: (1)属于直线的点,它的三个投影均属于直线的投影。反之,点三个投影均分别属于直 线的三个同名投影,则该点属于直线。如图4-5所示,已知C∈AB,则c∈ab、c'ea'b'、c∈ a"b”。 (2)属于线段的点,分线段之比等于点的投影分线段的同名投影之比。如图4-5所示,已 知C∈AB,则AC:CB=ac:cb=a'c':c'b'=a”e":c"b"。 【例42】已知线段AB投影,试将AB分成3:2两段,求分点C的投影(图4-6)。 解:见图4-6,过a任作一辅助线截等距五段,末端点B。,分点Co:连b,B。,过C。作bB,平 行线cCo,交ab于c;过C作OX轴垂线cc',交a'b'于c',即求得分点C的投影。 图45直线上的点 图46点分线段呈比例 第四节 两直线的相对位置 两直线的相对位置有三种情况:平行、相交和交叉(又称异面)。 一、平行两直线 如图4-7所示,两平行直线AB∥CD,根据平行投影的性质一空间平行两直线其投影相 图47平行两直线 .31
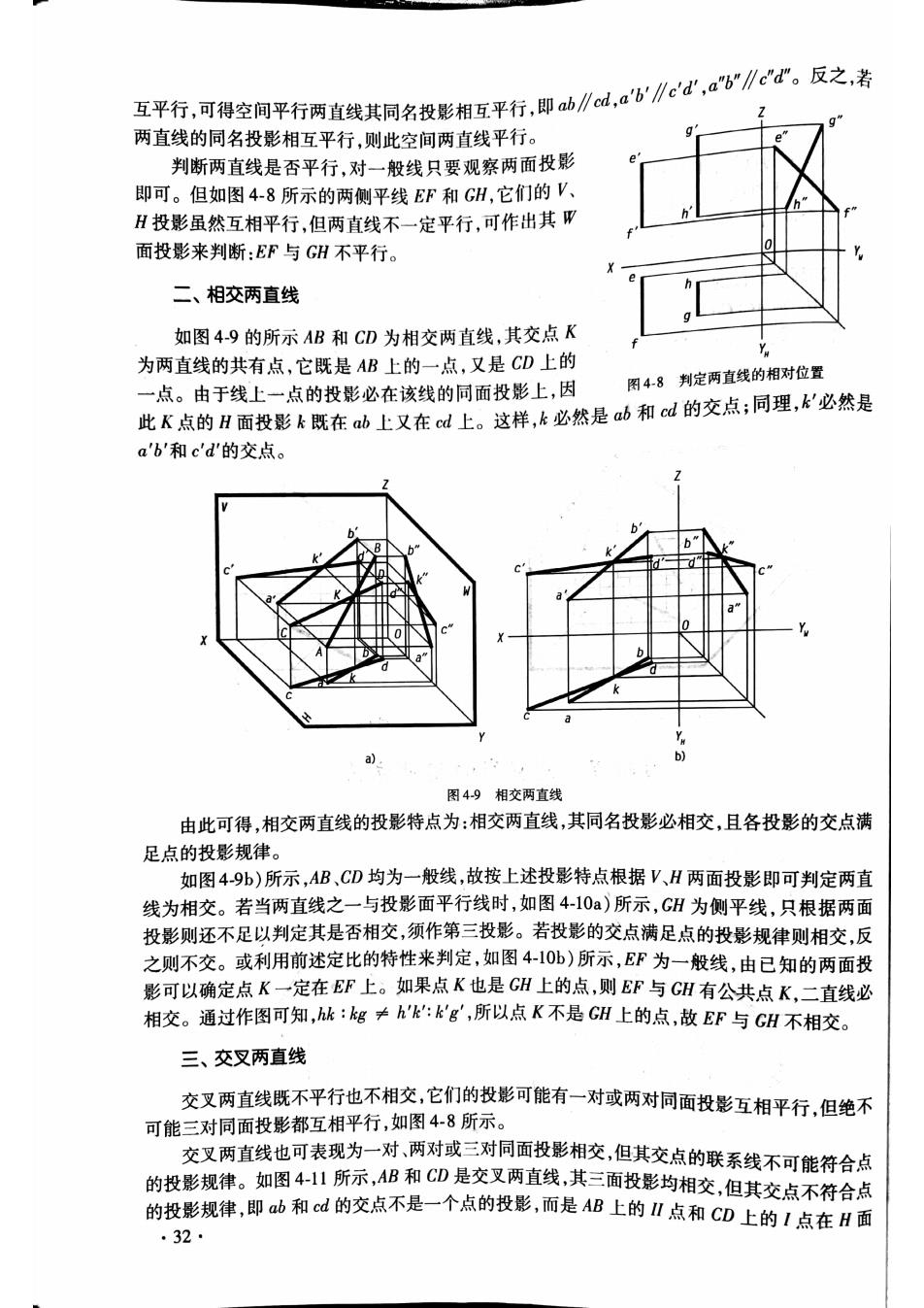
哥平行可得空间平行两直线其同名投影指互平行.即/do8e公,。:。反之,者 两直线的同名投影相互平行,则此空间两直线平行。 判断两直线是否平行,对一般线只要观察两面投影 即可。但如图48所示的两侧平线EF和GH,它们的V, H投影虽然互相平行,但两直线不一定平行,可作出其W 面投影来判断:EF与GH不平行。 二、相交两直线 如图49的所示AB和CD为相交两直线,其交点K 为两直线的共有点,它既是AB上的一点,又是CD上的 一点。由于线上一点的投影必在该线的同面投影上,因 图48判定两直线的相对位置 此K点的H面投影k既在b上又在d上。这样,k必然是b和d的交点;同理,k必然是 a'b和c'd的交点。 图49相交两直线 由此可得,相交两直线的投影特点为:相交两直线,其同名投影必相交,且各投影的交点满 足点的投影规律。 如图49b)所示,AB,CD均为一般线,故按上述投影特点根据V、H两面投影即可判定两直 线为相交。若当两直线之一与投影面平行线时,如图4-10a)所示,GH为侧平线,只根据两面 投影则还不足以判定其是否相交,须作第三投影。若投影的交点满足点的投影规律则相交,反 之则不交。或利用前述定比的特性来判定,如图410b)所示,EF为一般线,由已知的两面投 影可以确定点K一定在EF上。如果点K也是GH上的点,则EF与CH有公共点K,二直线必 相交。通过作图可知,k:g≠h'k:k'g,所以点K不是GH上的点,故EF与GH不相交。 三、交叉两直线 交又两直线既不平行也不相交,它们的投影可能有一对或两对同面投影互相平行,但绝不 可能三对同面投影都互相平行,如图48所示。 交叉两直线也可表现为一对,两对或三对同面投影相交,但其交点的联系线不可能符合点 的投影规律。如图4山所示,4B和D是交又两直线,其三面投影均相交,但其交点不符合点 的投影规律,即山和d的交点不是-个点的投影,而是B上的Ⅱ点和CD上的1点在H面 .32
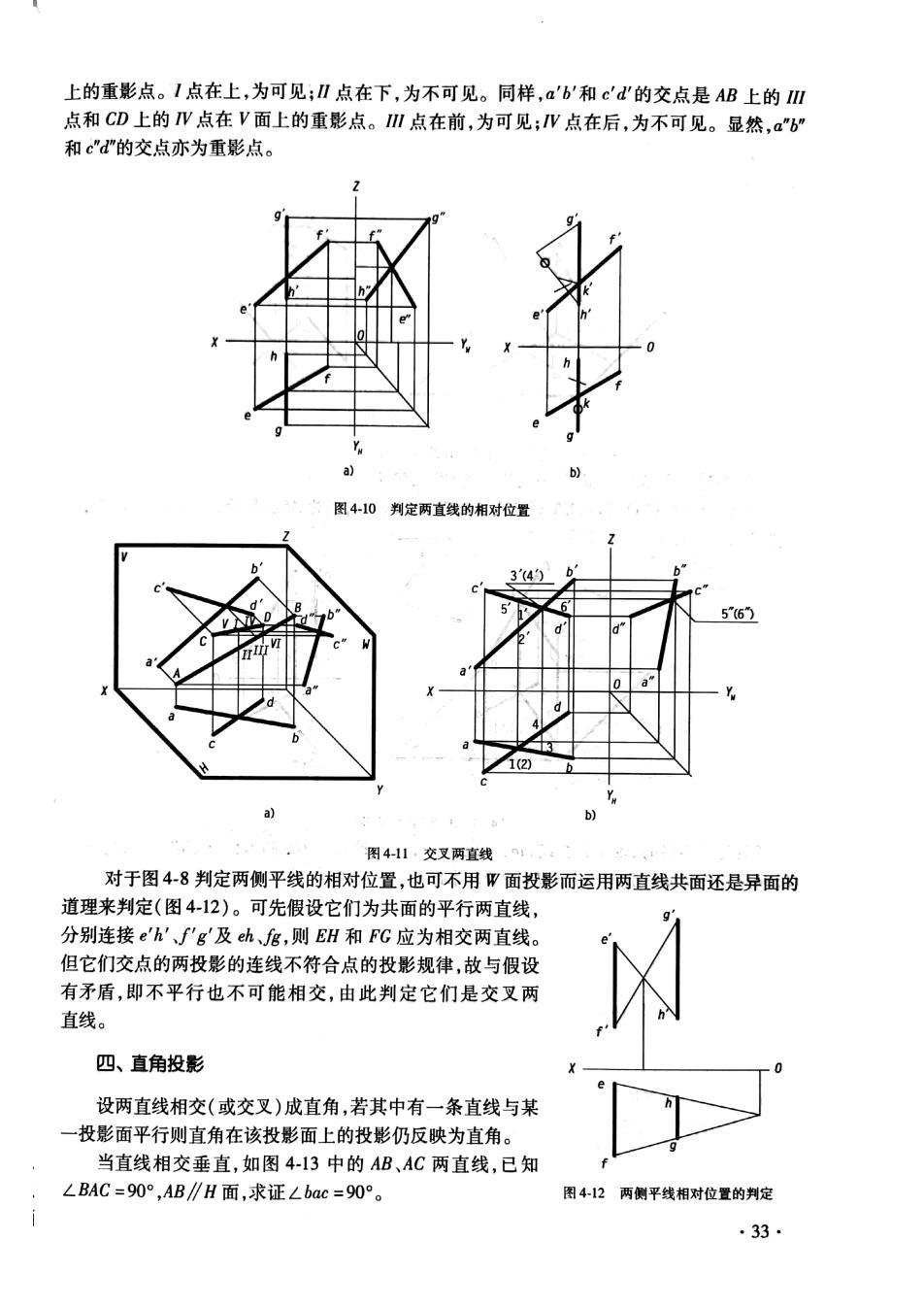
上的重影点。1点在上,为可见;Ⅱ点在下,为不可见。同样,a'b'和c'd的交点是AB上的Ⅲ 点和CD上的W点在V面上的重影点。Ⅲ点在前,为可见;V点在后,为不可见。显然,a"b” 和c"d”的交点亦为重影点。 图410判定两直线的相对位置 3(4 图4-11·交叉两直线 对于图4-8判定两侧平线的相对位置,也可不用W面投影而运用两直线共面还是异面的 道理来判定(图4-12)。可先假设它们为共面的平行两直线, 分别连接e''、f'g及eh、B,则EH和FG应为相交两直线 但它们交点的两投影的连线不符合点的投影规律,故与假设 有矛盾,即不平行也不可能相交,由此判定它们是交叉两 直线。 四、直角投影 设两直线相交(或交叉)成直角,若其中有一条直线与某 ~投影面平行则直角在该投影面上的投影仍反映为直角。 当直线相交垂直,如图4-13中的AB、AC两直线,已知 LBAC=90°,AB∥H面,求证Lbac=90°。 图412两侧平线相对位置的判定 .33

证明:因为ABAC,AB1,所以A银⊥rC.又因为AB/ab,所以ob1,因 当直线交又垂直时,如图413中的AB,MN丙直线,过A点作4C∥MW,则证明与直线有 此,∠bac=90° 交垂直时一样。 图413一直线平行于投影面的两相交(交叉)垂直直线的投是 【例43】求铅垂线AB与一般位置线CD之间的距离MN。 分析:如图4-14a)所示,MN为直线AB、CD的公垂线,因为AB⊥H面,所以MN∥H面,根 直角授影mn⊥cd即可求得。 图414求两直线的公垂线 解:见图4-14b),过a作直线mn⊥cd交cd于n,过n作OX轴垂线交c'd'于n',过n'作 OX轴平行线交'b'于m',mn=MN即为所求距离。 .34