
第六章 直线与平面的相对位置、 两平面的相对位置 直线与平面之间和两平面之间的相对位置可分为平行,相交及垂直三种。本章重点讨论 三个问题: (1)在投影图上如何绘制及判别直线与平面、平面与平面平行。 (2)如果直线与平面、平面与平面不平行,在投影图上如何求出它们的交点或交线, (3)在投影图上如何绘制及判别直线与平面、平面与平面垂直。 最后讨论距离和角度的度量,这是对以前各章原理的综合运用。 第一节·直线与平面、平面与平面平行 一、直线与平面平行 由初等几何知道,若一直线平行于属于定平面的一直线,则直线与该平面平行。如图6-1 所示,直线DE平行于属于定平面P的直线CF,则直线DE与该平面P平行。 【例6-1】试判断已知直线MW是否平行于定平面AB×CD(图6-2)。 分析:在图6-2中,mn平行于ab,而m'n'不平行于a'b',则MN不平行于AB,即平面上没 有与直线MN相平行的直线。所以,直线MN不平行于定平面。 6.1 直线与平面平行示意 断直线与平面是 例6-2 过已知点 线平导 知平面AB [图6-3a)] 41

分折:过在州了以作无方多素平行于已加华西的克我,房中只有康水年维先 已知学面的任-来羊我C0为籍时线图63b】,秀过点孔直维心年行于0, 行于属于定平面的水平线CD,所以MN既是水平线又平行于已知平面ABC。 二、两平面平行 从初等几何得知,若属于一平面的相交再直线对应平行于凤于另平面的相交两直线 此两平面平行。图64说明.两对相交直线B,8C和ABBC,分别属于平面P和Q。者精 对相交直线对应平行,则平面P,Q平行。 图64.平面与平面平行示意图 【例63】试判断两已知平面ABC和DEF是否平行[图6-5a)]。 分析:可先作属于第二平面的一对相交直线,再判断是否与第一平面的一对相交直线 对应平行。图65b)中,作属于第二平面的Dg和Eh,因为Dg∥AB,Eh∥AC,所以两平面 平行。 金为 图65判断两平面是否平行 【例64】巴知定平面由平行两直线AB和CD给定。试过定点K作一平面平行于已 平面[图6-6a)]。 分析:只要过点K做一对相交直线对应地平行于属于已知平面的一对相交直线,所作的 这对相交直线即可代表所求的平面。国66品)中,先在平面(AB/CD)上作与AB相交的直线 AD,再迹点K作KL∥AB,KM/AD,平面(KL×KM)即为所求平面。 若两平行平面同时鲁直来一投影面,则其积聚性的授影相互平行,如用67所示。 42

11.NiV 图66作平面平行于已知平面 图67两特殊位置平面平行 第二节直线与平面的交点、两平面的交线 直线与平面相交只有一个交点,它是直线和平面的共有点。它既属于直线,又属于平面。 两平面的交线是一直线,这条直线为两平面共有。共有性是求解相交问题依据的基本 特性。 一、特殊位置的相交 特殊位置的相交问题是指相交两元素中至少有一个垂直于投影面的情况。此时该元素的 个投影有积聚性,利用积聚性,即可求出交点或交线的投影。 1,直线与平面相交 如图6-8b)所示直线MW和铅垂面Q相交。平面Q的水平投影Qm积聚成一直线。交点 K既然是属于平面的点,那么它的水平投影一定属于平面Q的水平投影。交点K又属于直线 MN,它的水平投影必属于MW的水平投影。因此,水平投影mn与Qa的交点k便是交点K的 水平投影。然后在m'n上找出K的正面投影k,点K(k,k)即为直线MN和平面Q的交点。 图6-8a)为其直观图。 图6-8b)中,直线与平面的正面投影有一段重叠,即存在可见性问题。为了使图形明显起 见,把直线MW被平面Q遮住部分用虚线来表示。交点K是直线MW可见部分和不可见部分 ·43

的分界点,从水平投影可以看出,直线的K段在平面之前,X段在平面之后。所以m'化可 见,nk'与平面重叠部分不可见,即画成虚线。 6) 图68直线与特殊位置平面的交点 图6-9b)表示一铅垂线AB与平面CDEF相交。因交点K在AB上,故k与ab重合;因点 K又在平面CDEF上,故可利用平面上取点的方法,用辅助线(EG)求出K'。直线AB正面投影 的可见性,可利用平面上直线EF与直线AB的重影点H、1来判断。从水平投影上看,H比I离 OX轴近,即EF线上的点H在后,AB线上的点I在前,故'可见,ak'段也可见。 图6-9铅垂线与平面相交 2.两平面相交 通常,把求两平面交线的问题看作是求两个共有点或一个共有点及一确定的方向的问题。 从图610a)分析得知,要求图6-10b)中一般位置平面4MBC和铅垂面DEFG的交线,只要求出 属于交线的任意两点(如K和)即可。显然K.L即为AC,CB两边与铅垂面DEFC的交点。 平面D5FG是铅垂面,直线AC,BC与特殊位置平面交点的求法在前面已讨论,其作图过 程如图6-10b)所示,KL即为两平面的交线。 “当交线在平面图形的范围内时,甲,乙两平面投影重叠部分,其可见性总是以交线为界,如 果交线的一侧为甲面可见,则交线的另一侧必为乙面可见。图6,10b)中两平面正面投影的重 叠部分,从水平投影直观判断,交线右方三角形平面在前,故a0k?可见,:和了线中一段 应画成虚线;交线左方的四边形平面可见,三角形平面轮廓线被遮掩部分应画成虚线。 .44
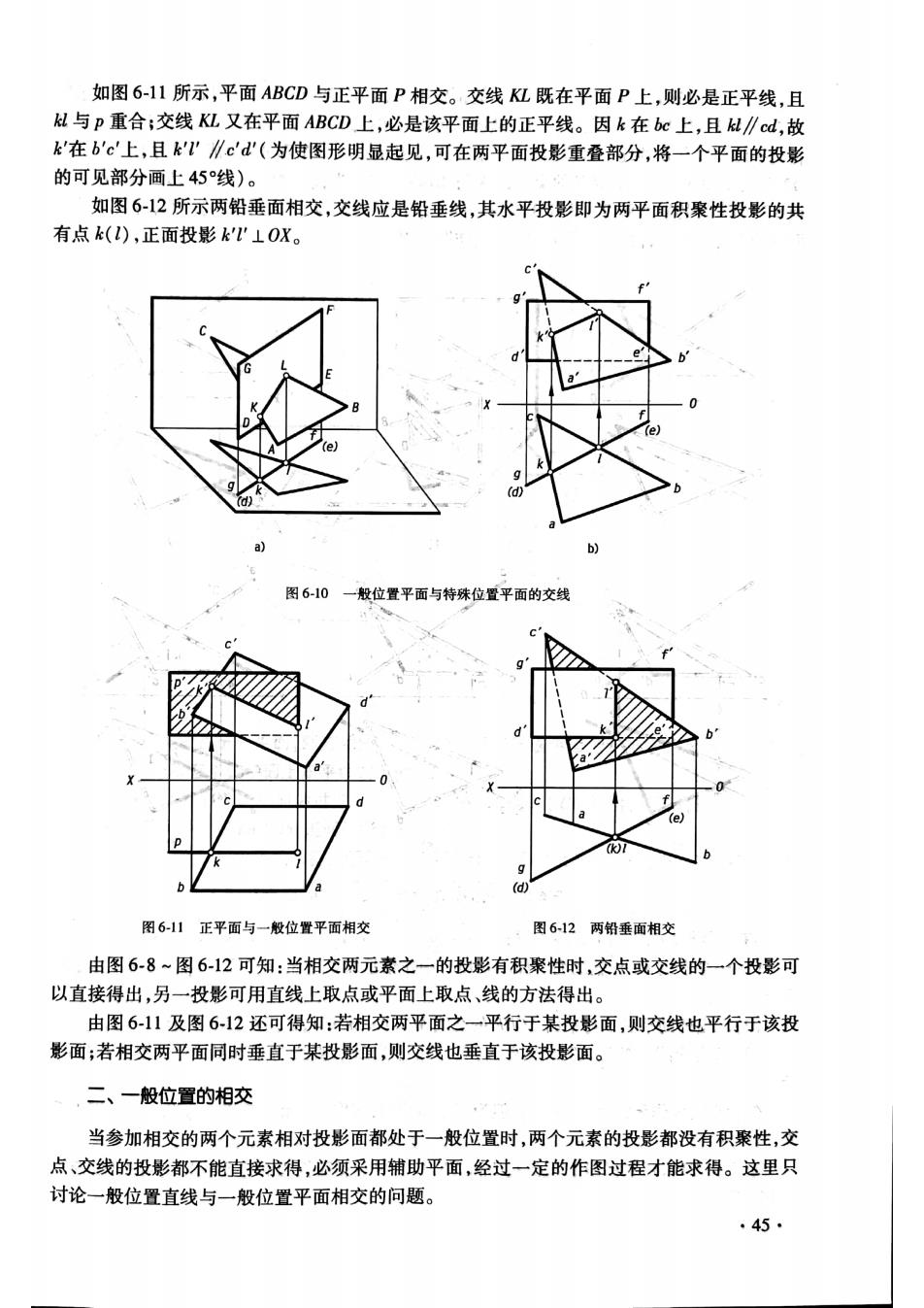
如图6-11所示,平面ABCD与正平面P相交。交线K亿既在平面P上,则必是正平线,且 M与p重合:交线KL又在平面ABCD上,必是该平面上的正平线。因k在bc上,且M∥d,故 k'在b'c上,且k'∥'d'(为使图形明显起见,可在两平面投影重叠部分,将一个平面的投影 的可见部分画上45线)。 如图6-12所示两铅垂面相交,交线应是铅垂线,其水平投影即为两平面积聚性投影的共 有点k(),正面投影kI'⊥OX。 殊位置平面 图611正平面与一般位置平面相交 图6-12两铅垂面相交 由图6-8~图6-12可知:当相交两元素之一的投影有积聚性时,交点或交线的一个投影可 以直接得出,另一投影可用直线上取点或平面上取点、线的方法得出。 由图611及图612还可得知:若相交两平面之一平行于某投影面,则交线也平行于该投 影面;若相交两平面同时垂直于某投影面,则交线也垂直于该投影面 二、一般位置的相交 当参加相交的两个元素相对投影面都处于一般位置时,两个元素的投影都没有积聚性,交 点、交线的投影都不能直接求得,必须采用辅助平面,经过一定的作图过程才能求得。这里只 讨论一般位置直线与一般位置平面相交的问题。 .45
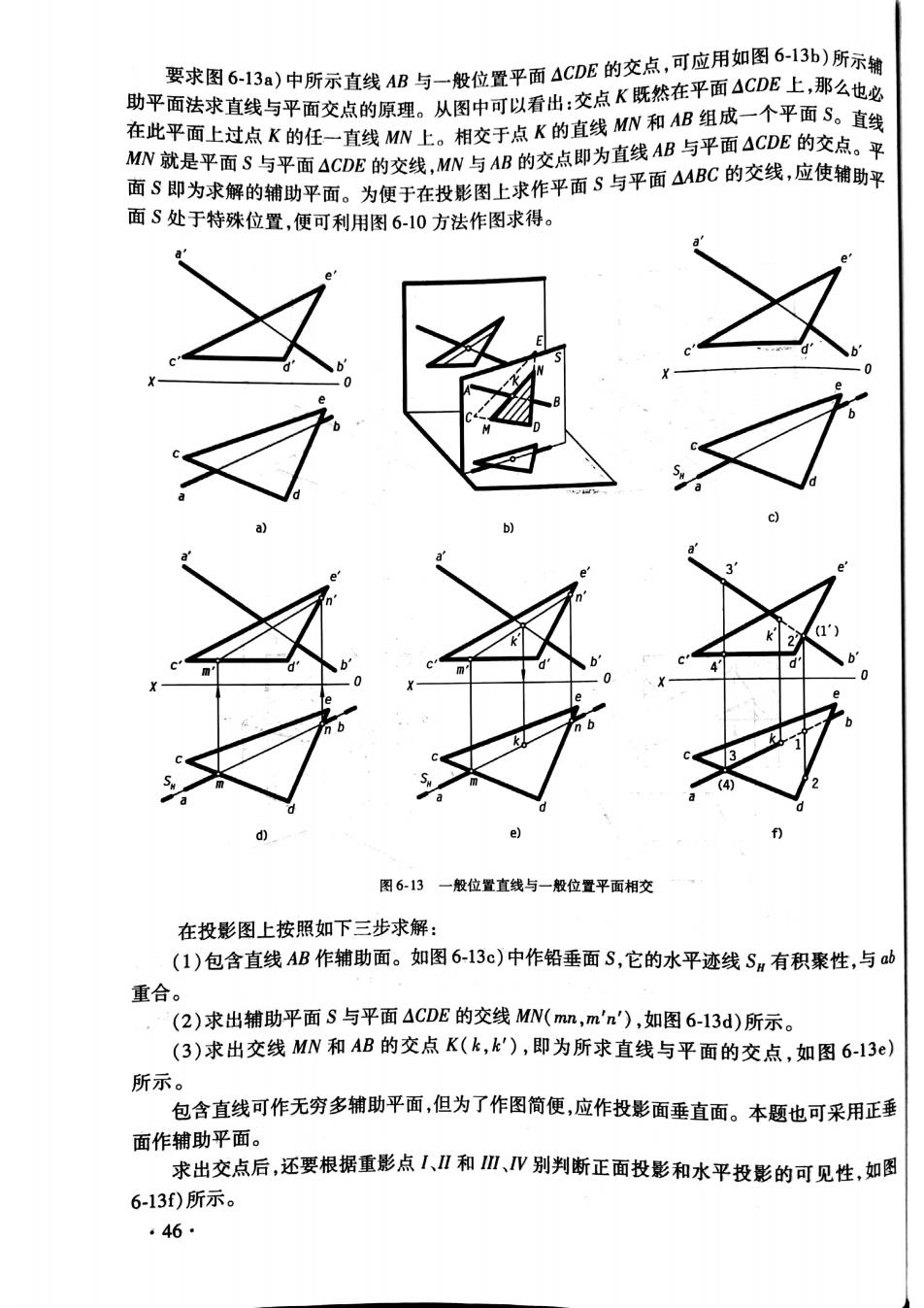
要求图6-13a)中所示直线AB与一般位置平面4GDB的交点,可应用如图6-13b)所示输 助子面法求直线与平面交点的原定。从图中可以看击:交点人既然在平面4CE上,聚么使么 在此平面上过点K的任一直线MN上。相交于点K的直线MN和AB组成一个平面S。直线 MN就是平面S与平面4CDE的交线,MN与B的交点即为直线AB与平面4CDE的交点。平 面8即为求解的辅助平面。为便于在投影图上求作平面3与平面4MBC的交线,应使辅助平 面S处于特殊位置,便可利用图6-10方法作图求得。 图6-13一般位置直线与一般位置平面相交 在投影图上按照如下三步求解: (1)包含直线4B作辅助面。如图6-13c)中作铅垂面S,它的水平迹线Sn有积聚性,与d 重合。 (2)求出辅助平面S与平面4CDE的交线MN(mn,m'n'),如图6-13d)所示。 (3)求出交线MN和AB的交点K(k,k'),即为所求直线与平面的交点,如图6-13) 所示 包含直线可作无穷多辅助平面,但为了作图简便,应作投影面垂直面。本题也可采用正垂 面作辅助平面。 求出交点后,还要根据重影点1人Ⅱ和Ⅲ、V别判断正面投影和水平投影的可见性,如图 6-13f)所示。 ·46

第三节直线与平面垂直、两平面垂直 一、直线与平面垂直 垂直于平面的直线,称为该平面的垂线或法线。 初等几何定理:若一直线垂直于某平面,则此直线必垂直于该平面上的一切直线。在图 6-14a)中,若直线M垂直于平面P,则其必垂直于属于平面P的一切直线,其中包括水平线 AB和正平线CD。根据直角投影定理,投影图上必表现为直线LM的水平投影垂直于水平线 AB的水平投影(m⊥ab),直线M的正面投影垂直于正平线CD的正面投影(L'm'⊥c'd')。由 此可得直线与平面垂直的投影定理: 图6-14直线与平面垂直 若一直线垂直于一平面,则直线的水平投影必垂直于该平面上水平线的水平投彩,直线 的正面投影必垂直于该平面上正平线的正面投影。 如图6-14b)所示,定平面为过点K的水平线AB和正平线CD给出,若要直线LM垂直于 该平面,则其水平投影lm⊥ab,正面投影'm'⊥c'd'。 反之,若一直线的水平投影垂直于属于定平面上水平线的水平投影;直线的正面投影垂直 于属于定平面上正平线的正面投彩,则直线必垂直于该平面。 这是因为直线和平面垂直的必要和充分条件是,该直线垂直于属于平面的相交两直线: 需要注意:国614中,M与AB、CD是不相交的。若要求法线的垂足,必须按直线与平 面求交点的作图方法求得。 【例65】已知定平面由平行两直线AB和CD给定,试判断直线是否垂直于定平面 (图6-15)。 分析:直线AB和CD是水平线。作属于定平面的任意正平线ED(ed,ed')。M⊥cd,但 '不垂直于e'd',故直线KL不垂直于定平面。 平面法线的作困与判断,要依赖属于该平面的投影面平行线的方向。这与前面学习的 平面的最大斜度线有类似之处。但必须分清:法线与平面垂直在平面之外,而最大斜度线 在平面之内:作法线需依靠两个面内投形面的平行线,而作最大斜度线只需一个面内投影 面的平行线。 47
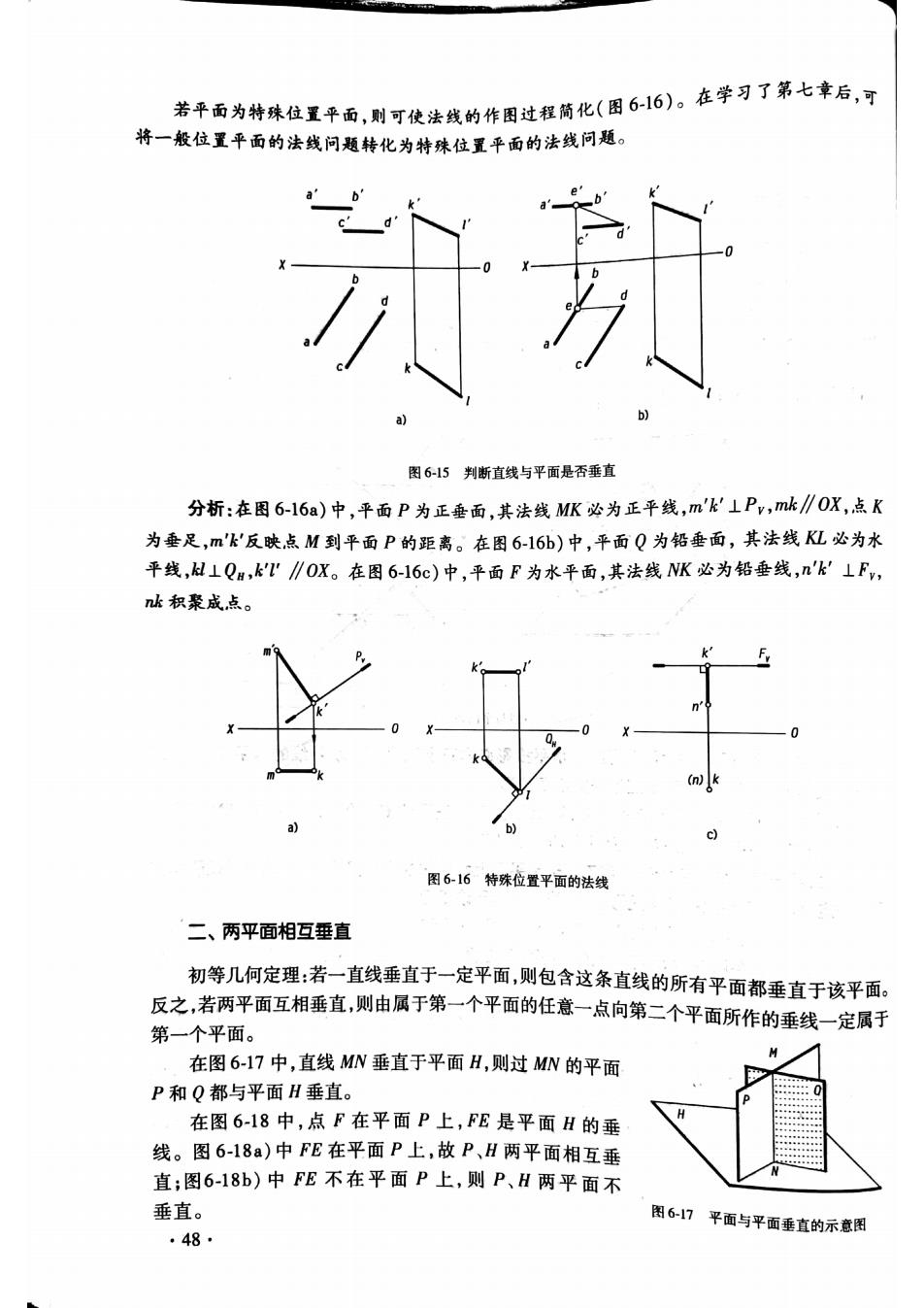
者年西为特珠位里平面,则可代法城的作国过红简化(因6:6)。在学习了第七幸后,于 将一搬位里平面的法线问题转化为特殊位置平面的法线问题。 次贸 图6-15判断直线与平面是否垂直 分析:在图6-16a)中,平面P为正垂面,其法线MK必为正平线,m'k⊥Pv,mk∥0X,点K 为垂足,m'k'反映点M到平面P的距离。在图6-16b)中,平面Q为铅垂面,其法线L必为水 平线,H1Qa,kT∥OX。在图6-16c)中,平面F为水平面,其法线NK必为铅垂线,n'K⊥F, nk积聚成点」 ¥… 图616特殊位置平面的法线 二、两平面相互垂直 初等儿何定理:若一直线垂直于一定平面,则包含这条直线的所有平面都垂直于该平面。 反之,若两平面互相垂直,则由属于第一个平面的任意一点向第二个平面所作的垂线一定属于 第一个平面。 在图6-17中,直线MN垂直于平面H,则过MN的平面 P和Q都与平面H垂直。 在图6-18中,点F在平面P上,FE是平面H的垂 线。图6-18a)中FE在平面P上,故P、H两平面相互垂 直:图6-18b)中FE不在平面P上,则P、H两平面不 垂直。 ·48 图6-7平面与平面垂直的示意图
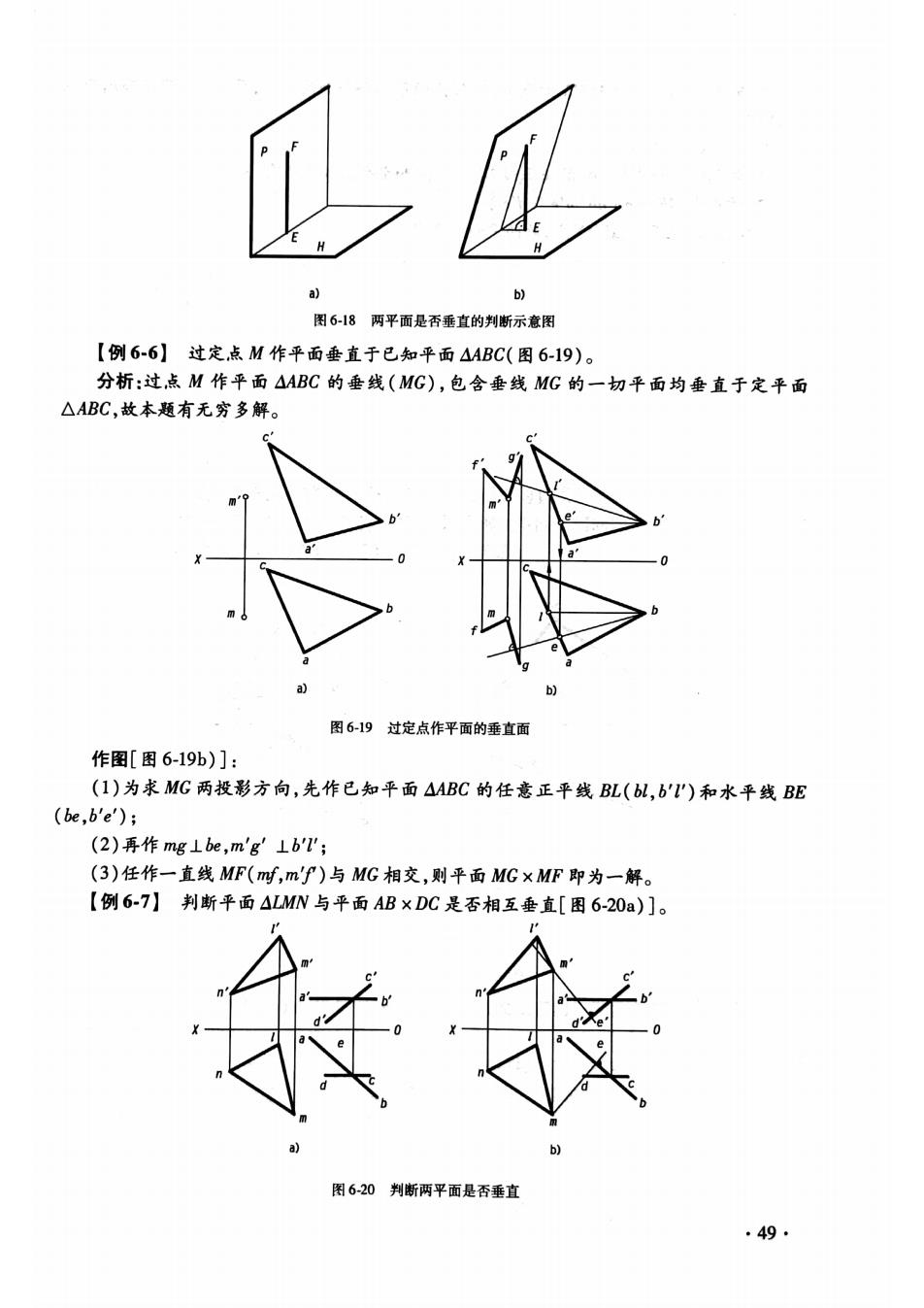
a) 图6-18两平面是否垂直的判断示意图 【例6-6】过定点M作平面垂直于已知平面△ABC(图6-19)。 分析:过点M作平面△ABC的垂线(MG),包含垂线MG的一切平面均垂直于定平面 △ABC,故本题有无穷多解。 图6-1 过定点作平面的垂直面 作图[图6-19b)]: (1)为求MG两投影方向,先作已知平面△ABC的任意正平线BL(bL,b'')和水平线BE (be,b'e'); (2)再作mg⊥be,m'g'⊥b'; (3)任作一直线MF(m时,mP)与MG相交,则平面MG×MF即为一解。 【例6-7】判断平面ALMN与平面AB×DC是否相互垂直[目 16-20a)1 太 图620判断两平面是否垂直 .49

分新:任取属于平面的点以.过V点联第二个年面的套线,再检壶金线是香马4 面△LMN。 作图[图6-20b)]: I)作属于平面ABx DC的正平钱DC(已有)和水平线AB(已有): (2)作垂线ME(me Lab,m'e'1d'c')。 显然ME不在平面4MN上,故两平而不垂直 .50