
常用中规模组合逻辑电路 信息学院实验中心
常用中规模组合逻辑电路 信息学院实验中心

MSI ·集成电路由SS发展到MSI、LSIVLS后,单个芯片的功能 大大增强。一般地,在SS中仅是基本器件(如逻辑门或触发 器)的集成,在MS中已是逻辑部件(如译码器、寄存器等)的 集成,而在LS和VLSI中则是一个数字子系统或整个数字系统 (如微处理器)的集成。因此,采用中、大规模集成电路组成数 字系统具有体积小、功耗低、可靠性高等优点,且易于设计、 调试和维护。 ·各种中规模通用集成电路本身就是一种完美的逻辑设计作品, 使用时只需适当地进行连接,就能实现预定的逻辑功能。另 外,由于它们所具有的通用性、灵活性及多功能性,使之除 完成基本功能之外,还能以它们为基本部件组成电路,有效 地实现各种逻辑功能。因此,必须熟悉其功能、特点和使用 方法,这样才能恰当地、灵活地、充分地利用它们完成各种 逻辑电路的设计。 ·本章主要讨论最常用的几种中规模通用集成电路及其应用
MSI ▪ 集成电路由SSI发展到MSI、LSI和VLSI后,单个芯片的功能 大大增强。一般地,在SSI中仅是基本器件(如逻辑门或触发 器)的集成,在MSI中已是逻辑部件(如译码器、寄存器等)的 集成,而在LSI和VLSI中则是一个数字子系统或整个数字系统 (如微处理器)的集成。因此,采用中、大规模集成电路组成数 字系统具有体积小、功耗低、可靠性高等优点,且易于设计、 调试和维护。 ▪ 各种中规模通用集成电路本身就是一种完美的逻辑设计作品, 使用时只需适当地进行连接,就能实现预定的逻辑功能。另 外,由于它们所具有的通用性、灵活性及多功能性,使之除 完成基本功能之外,还能以它们为基本部件组成电路,有效 地实现各种逻辑功能。因此,必须熟悉其功能、特点和使用 方法,这样才能恰当地、灵活地、充分地利用它们完成各种 逻辑电路的设计。 ▪ 本章主要讨论最常用的几种中规模通用集成电路及其应用

常用中规模组合逻辑电路 Ucc B3 A3 F3 A B F FC ·使用最广泛的中规模组合逻辑集成电路 16 有二进制并行加法器、译码器、编码器、 T693(T692) 多路选择器和多路分配器等。 ·二进制并行加法器 -二进制并行加法器是一种能并行产生 F2B2A2F1A1BCo地 两个二进制数算术和的逻辑部件,按其 进位方式的不同可分为串行进位和超前 进位二进制并行加法器。 F F3 F2 F1 -目前常用的串行进位4位二进制并行加 法器有T692,超前进位4位二进制并行 FC T693(T692) 加法器有T693。其芯片的管脚排列图 A A3 A2 A B Ba B2 B 和逻辑符号分别如右上图和右下图。图 中,A4、A3、A2、A1是二进制被加数; B4、B3、B2、B1是二进制加数;C0 工。h2Hh△) ■AA白白H
常用中规模组合逻辑电路 ▪使用最广泛的中规模组合逻辑集成电路 有二进制并行加法器、译码器、编码器、 多路选择器和多路分配器等。 ▪二进制并行加法器 –二进制并行加法器是一种能并行产生 两个二进制数算术和的逻辑部件,按其 进位方式的不同可分为串行进位和超前 进位二进制并行加法器。 –目前常用的串行进位4位二进制并行加 法器有T692,超前进位4位二进制并行 加法器有T693。其芯片的管脚排列图 和逻辑符号分别如右上图和右下图。图 中,A4、A3、A2、A1是二进制被加数; B4、B3、B2、B1是二进制加数;C0 为低位的进位输入;FC4为高位的进位 输出; 、 、 、 为相加的和数

二 进制并行加法器 ·串行进位三进制并行加法器是由全 加器级联而成的。其特点是:被加 数和加数的各位能同时并行到达各 位的输入端,而各位全加器的进位 输入则是按照由低位向高位逐级串 行传递的,各进位形成一个进位链 由于每一位相加的和都与本位进位 输入有关,所以,最高位必须等到 各低位全部相加完成并送来进位信 号之后才能产生运算结果。显然, 这种加法器运算速度较慢,而且位 数越多,速度就越低
二进制并行加法器Ⅰ ▪串行进位二进制并行加法器是由全 加器级联而成的。其特点是:被加 数和加数的各位能同时并行到达各 位的输入端,而各位全加器的进位 输入则是按照由低位向高位逐级串 行传递的,各进位形成一个进位链。 由于每一位相加的和都与本位进位 输入有关,所以,最高位必须等到 各低位全部相加完成并送来进位信 号之后才能产生运算结果。显然, 这种加法器运算速度较慢,而且位 数越多,速度就越低

进制并行加法器▣ ·为了提高加法器的运算速度,必须设法减小或去除由于进位 信号逐级传送所花的时间,使各位的进位直接由加数和被加数 来决定,而不需依赖低位进位。根据这一思想设计的加法器称 为超前进位(又称先行进位)二进制并行加法器。 ■根据全加器的“进位”输出表达式 Ci=AiBi+(Ai+Bi)Ci-1 可知:当第i位的被加数Ai和加数B均为1时,有AB1,不论 低位运算结果如何,本位必然产生进位输出,即C=1,所以, 定义Gi=AiBi为进位产生函数;当Ai和Bi中只有一个为1时,即 AiBi=0,Ai+Bi=1时,可使得Ci=Ci-1,即当Ai+B=1时,来自 低位的进位输入能传送到本位的进位输出。所以,定义 Pi=Ai+Bi为进位传递函数,将P和Gi代人全加器的“和”及 “进位”输出表达式,可得到 Fi=Ai⊕Bi⊕Ci-1=PiGi⊕Ci-1 Ci=AiBi+(Ai+B)Ci-1=Gi+PiCi-1
二进制并行加法器Ⅱ ▪为了提高加法器的运算速度,必须设法减小或去除由于进位 信号逐级传送所花的时间,使各位的进位直接由加数和被加数 来决定,而不需依赖低位进位。根据这一思想设计的加法器称 为超前进位(又称先行进位)二进制并行加法器。 ▪根据全加器的“进位”输出表达式 Ci=AiBi+(Ai+Bi)Ci-1 可知:当第i位的被加数Ai和加数Bi均为1时,有AiBi=1,不论 低位运算结果如何,本位必然产生进位输出,即Ci=1,所以, 定义Gi=AiBi为进位产生函数;当Ai和Bi中只有一个为1时,即 AiBi=0,Ai+Bi=1时,可使得Ci=Ci-1,即当Ai+Bi=1时,来自 低位的进位输入能传送到本位的进位输出。所以,定义 Pi=Ai+Bi为进位传递函数,将Pi和Gi代人全加器的“和”及 “进位”输出表达式,可得到 Fi=Ai⊕Bi⊕Ci-1=PiGi’ ⊕Ci-1 Ci=AiBi+(Ai+B)Ci-1=Gi+PiCi-1
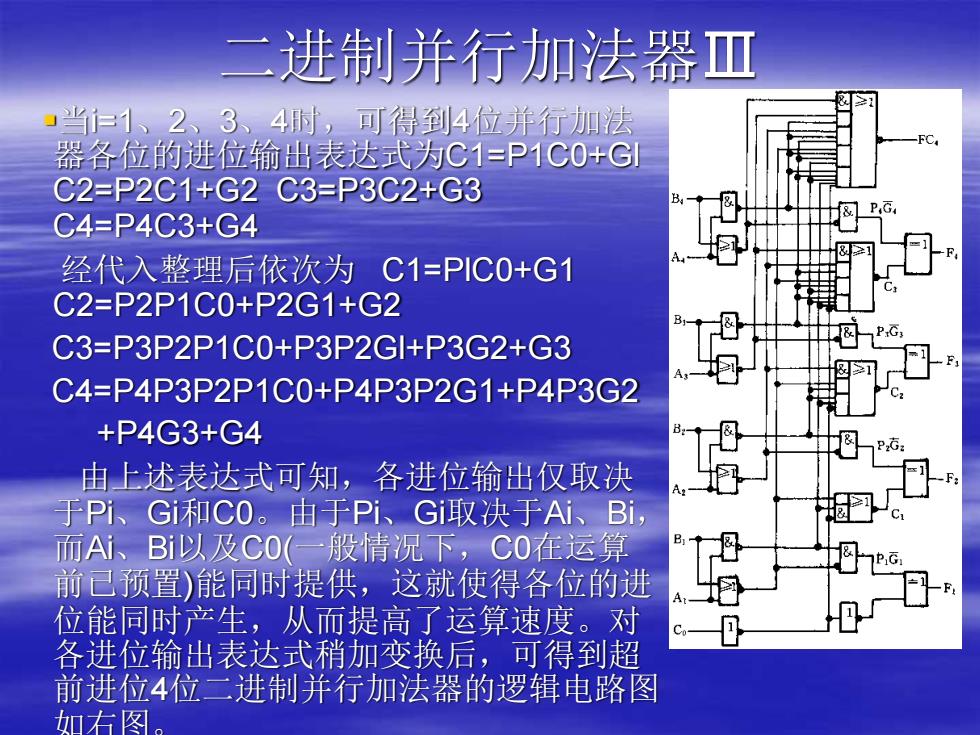
二进制并行加法器Ⅲ ·当仁1、2、3、4时,可得到4位并行加法 器各位的进位输出表达式为C1=P1C0+G C2=P2C1+G2C3=P3C2+G3 C4=P4C3+G4 经代入整理后依次为C1=PIC0+G1 C2=P2P1C0+P2G1+G2 C3=P3P2P1C0+P3P2GI+P3G2+G3 C4=P4P3P2P1C0+P4P3P2G1+P4P3G2 +P4G3+G4 由上述表达式可知,各进位输出仅取决 于Pi、Gi和C0。由于Pi、Gi取决于Ai、Bi, 而Ai、Bi以及C0(一般情况下,C0在运算 前己预置)能同时提供,这就使得各位的进 位能同时产生,从而提高了运算速度。对 各进位输出表达式稍加变换后,可得到超 前进位4位二进制并行加法器的逻辑电路图 如右图
二进制并行加法器Ⅲ ▪当i=1、2、3、4时,可得到4位并行加法 器各位的进位输出表达式为C1=P1C0+Gl C2=P2C1+G2 C3=P3C2+G3 C4=P4C3+G4 经代入整理后依次为 C1=PlC0+G1 C2=P2P1C0+P2G1+G2 C3=P3P2P1C0+P3P2Gl+P3G2+G3 C4=P4P3P2P1C0+P4P3P2G1+P4P3G2 +P4G3+G4 由上述表达式可知,各进位输出仅取决 于Pi、Gi和C0。由于Pi、Gi取决于Ai、Bi, 而Ai、Bi以及C0(一般情况下,C0在运算 前已预置)能同时提供,这就使得各位的进 位能同时产生,从而提高了运算速度。对 各进位输出表达式稍加变换后,可得到超 前进位4位二进制并行加法器的逻辑电路图 如右图
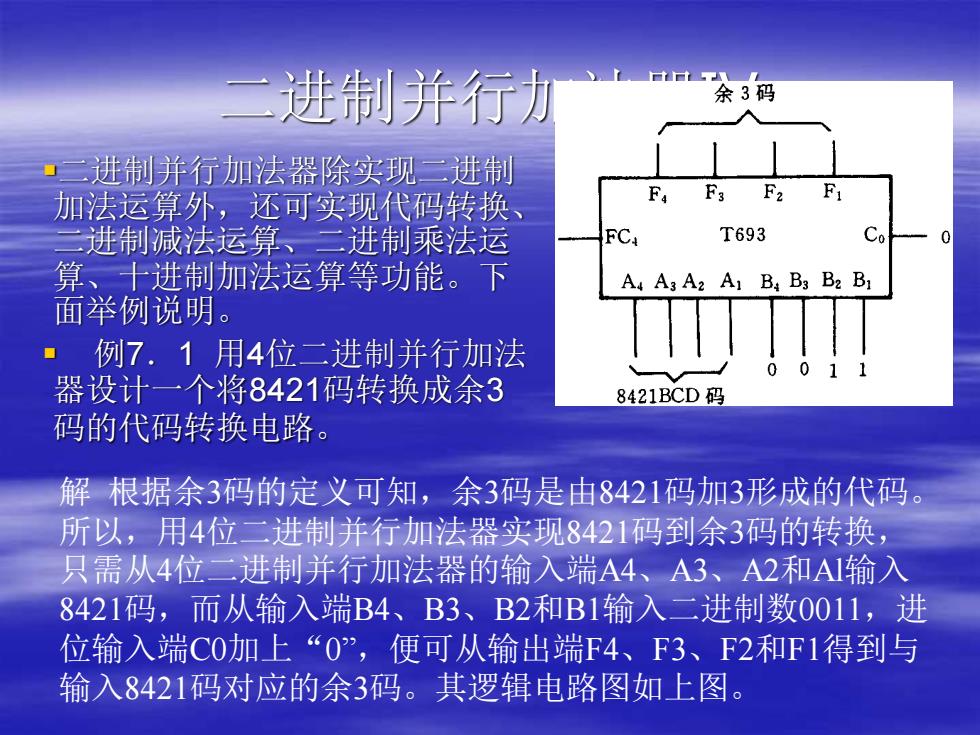
进制并行力 余3码 ·三进制并行加法器除实现二进制 加法运算外,还可实现代码转换 F F3 F2 F 二进制减法运算、二进制乘法运 FC T693 Co 算、十进制加法运算等功能。下 A A3 A2 A1 B B3 B2 B1 面举例说明。 例7.1用4位二进制并行加法 001 器设计一个将8421码转换成余3 8421BCD码 码的代码转换电路。 解根据余3码的定义可知,余3码是由8421码加3形成的代码 所以,用4位二进制并行加法器实现8421码到余3码的转换, 只需从4位二进制并行加法器的输入端A4、A3、A2和A1输入 8421码,而从输入端B4、B3、B2和B1输入二进制数0011,进 位输入端C0加上“0”,便可从输出端F4、F3、F2和F1得到与 输入8421码对应的余3码。其逻辑电路图如上图
二进制并行加法器Ⅳ ▪二进制并行加法器除实现二进制 加法运算外,还可实现代码转换、 二进制减法运算、二进制乘法运 算、十进制加法运算等功能。下 面举例说明。 ▪ 例7.1 用4位二进制并行加法 器设计一个将8421码转换成余3 码的代码转换电路。 解 根据余3码的定义可知,余3码是由8421码加3形成的代码。 所以,用4位二进制并行加法器实现8421码到余3码的转换, 只需从4位二进制并行加法器的输入端A4、A3、A2和Al输入 8421码,而从输入端B4、B3、B2和B1输入二进制数0011,进 位输入端C0加上“0”,便可从输出端F4、F3、F2和F1得到与 输入8421码对应的余3码。其逻辑电路图如上图
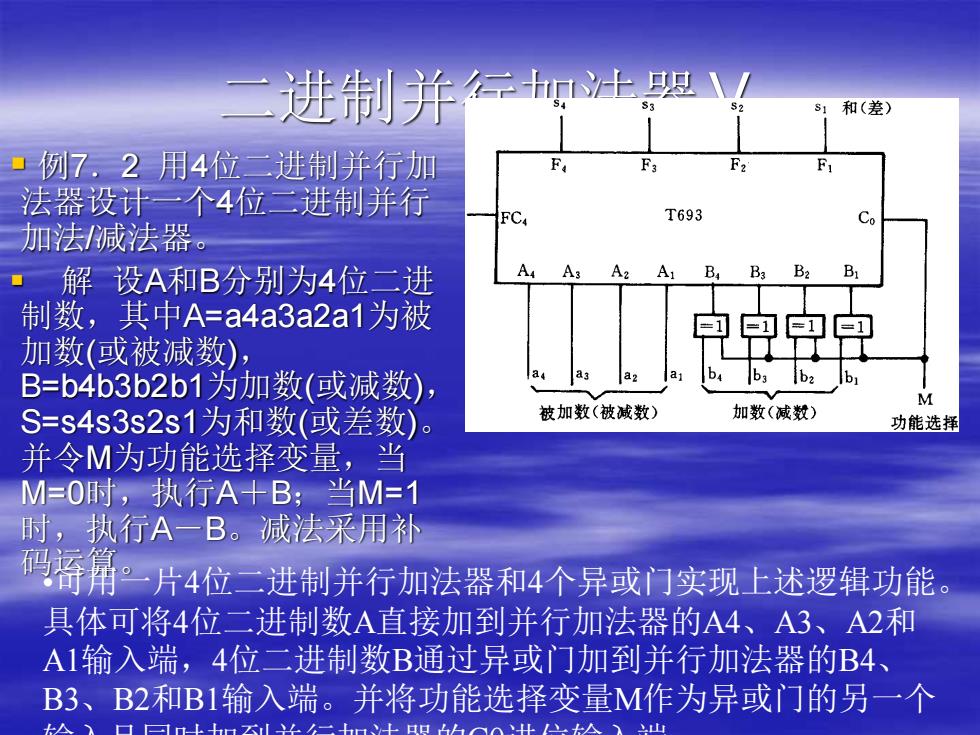
二进制并 云土盟☑ 和(差) ·例7,2用4位二进制并行加 法器设计一个4位二进制并行 FCA T693 加法/减法器。 ·解设A和B分别为4位二进 A A3 A2 A1 B Ba B2 B1 制数,其中A=a4a3a2a1为被 加数(或被减数), 电电中电 B=b4b3b2b1为加数(或减数) S=S4s3s2s1为和数(或差数)。 被加数(被减数) 加数(减数) 功能选择 并令M为功能选择变量,当 =0时,执行A+B;当M=1 时,执行A一B。减法采用补 码语第片4位二进制并行加法器和4个异或门实现上述逻辑功能 具体可将4位二进制数A直接加到并行加法器的A4、A3、A2和 A1输入端,4位二进制数B通过异或门加到并行加法器的B4、 B3、B2和B1输入端。并将功能选择变量M作为异或门的另一个 人日可m上hm云l4二hm4g4。nH八人)山
二进制并行加法器Ⅴ ▪ 例7.2 用4位二进制并行加 法器设计一个4位二进制并行 加法/减法器。 ▪ 解 设A和B分别为4位二进 制数,其中A=a4a3a2a1为被 加数(或被减数), B=b4b3b2b1为加数(或减数), S=s4s3s2s1为和数(或差数)。 并令M为功能选择变量,当 M=0时,执行A+B;当M=1 时,执行A-B。减法采用补 码运算。 •可用一片4位二进制并行加法器和4个异或门实现上述逻辑功能。 具体可将4位二进制数A直接加到并行加法器的A4、A3、A2和 A1输入端,4位二进制数B通过异或门加到并行加法器的B4、 B3、B2和B1输入端。并将功能选择变量M作为异或门的另一个 输入且同时加到并行加法器的C0进位输入端
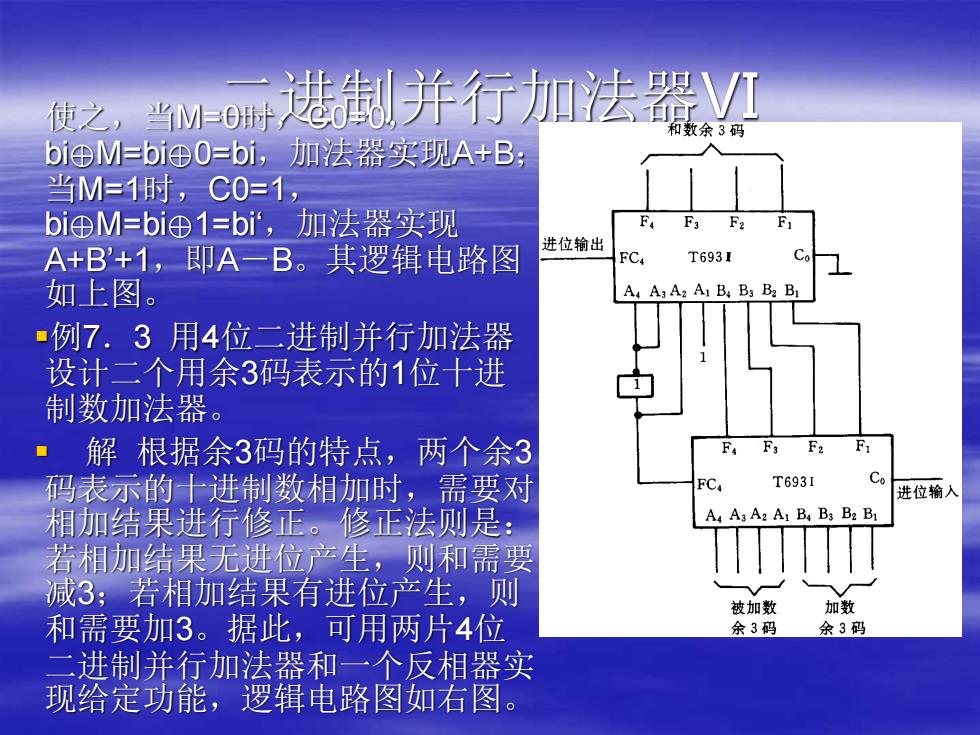
使之, 当w港制并行加法器 和数余3码 oi⊕M=bi⊕0=bi,加法器实现A+B, 当M=1时,C0=1 bi⊕M=bi⊕1=bi,加法器实现 F F3 F2 F 进位输出 A+B+1,即A一B。其逻辑电路图 FC T693I 如上图。 A A3 A2 A B B3 B2 B1 ·例7.3用4位二进制并行加法器 设计二个用余3码表示的1位十进 制数加法器。 ·解根据余3码的特点,两个余3 码表示的十进制数相加时,需要对 T693I 进位输入 相加结果进行修正。修正法则是: A A3 A2 A:BB:B2 B 若相加结果无进位产生,则和需要 减3;若相加结果有进位产生,则 被加数 加数 和需要加3。据此,可用两片4位 余3码 余3码 二进制并行加法器和一个反相器实 现给定功能,逻辑电路图如右图
使之,当M=0二进制并行加法器 时,C0=0, Ⅵ bi⊕M=bi⊕0=bi,加法器实现A+B; 当M=1时,C0=1, bi⊕M=bi⊕1=bi‘,加法器实现 A+B’+1,即A-B。其逻辑电路图 如上图。 ▪例7.3 用4位二进制并行加法器 设计二个用余3码表示的1位十进 制数加法器。 ▪ 解 根据余3码的特点,两个余3 码表示的十进制数相加时,需要对 相加结果进行修正。修正法则是: 若相加结果无进位产生,则和需要 减3;若相加结果有进位产生,则 和需要加3。据此,可用两片4位 二进制并行加法器和一个反相器实 现给定功能,逻辑电路图如右图

二进制并行加法器Ⅶ ·其中,片工用来对两个1位十进制数的余3码进行相加,片Ⅱ 用来对相加结果进行修正。修正控制函数为片I的进位输出 FC4,当FC4=0时,将片I的和输出送至片Ⅱ,并将其加上 二进制数1101(即采用补码实现运算结果减二进制数0011): 当FC4=1时,将片I的和输出送至片Ⅱ,并将其加上二进制 数0011,片Ⅱ的和输出即为两余3码相加的和数。 例7.4用4位二进制并行加法器实现4位二进制数乘法器的 逻辑功能。 ◆ 解设两个无符号4位二进制数X和Y,X=x3x2x1x0, Y=y3y2y小y0,则X和Y的乘积Z为一个8位二进制数, 可可令 Z=Z7Z6Z5Z4Z3Z2ZZ0。两数相乘求积的过程如下:因为两 个1位二进制数相乘的法则和逻辑“与”运算法则相同,所 以“积”项xyi0,j=0,1,2,3)可用两输入与门实现。而 对部分积求和则可用并行加法器实现。由此可知,实现4位 二进制数乘法运算的逻辑电路可由16个两输入与门和3个4位 二进制并行加法器构成。逻辑电路图如下图
二进制并行加法器Ⅶ ▪ 其中,片Ⅰ用来对两个1位十进制数的余3码进行相加,片Ⅱ 用来对相加结果进行修正。修正控制函数为片Ⅰ的进位输出 FC4,当FC4=0时,将片Ⅰ的和输出送至片Ⅱ,并将其加上 二进制数1101(即采用补码实现运算结果减二进制数0011); 当FC4=1时,将片Ⅰ的和输出送至片Ⅱ,并将其加上二进制 数0011,片Ⅱ的和输出即为两余3码相加的和数。 ▪ 例7.4 用4位二进制并行加法器实现4位二进制数乘法器的 逻辑功能。 ▪ 解 设两个无符号4位二进制数X和Y,X=x3x2x1x0, Y=y3y2yly0,则X和Y的乘积Z为一个8位二进制数,可令 Z=Z7Z6Z5Z4Z3Z2ZlZ0。两数相乘求积的过程如下:因为两 个1位二进制数相乘的法则和逻辑“与”运算法则相同,所 以“积”项xiyi(i,j=0,1,2,3)可用两输入与门实现。而 对部分积求和则可用并行加法器实现。由此可知,实现4位 二进制数乘法运算的逻辑电路可由16个两输入与门和3个4位 二进制并行加法器构成。逻辑电路图如下图