
第五章时序逻辑电路 。5.1概述☑ 。5.2时序逻辑电路的分析方法D 。5.3若干常用的时序逻辑电路 。5.4时序逻辑电路的设计方法) 。5.5时序逻辑电路中的竞争一冒险现象> 2006年 新疆大学信息科学与工程学院
2006年 新疆大学信息科学与工程学院 第五章 时序逻辑电路 ⚫ 5.1 概述 ⚫ 5.2 时序逻辑电路的分析方法 ⚫ 5.3 若干常用的时序逻辑电路 ⚫ 5.4 时序逻辑电路的设计方法 ⚫ 5.5 时序逻辑电路中的竞争-冒险现象

5.1概述 定义:时序逻辑电路在任一时刻的输出不仅取决 于当时的输入信号,而且还取决于电路的原来 状态(或者说,还与以前的输入有关 》 电路构成: 存储电路(主要是触发器,必不可少 组合逻辑电路(可选)。 时序逻辑电路的状态是由存储电路来记☑ 和表示的。 2006年 新疆大学信息科学与工程学院 返回目禄
2006年 新疆大学信息科学与工程学院 定义:时序逻辑电路在任一时刻的输出不仅取决 于当时的输入信号,而且还取决于电路的原来 状态(或者说,还与以前的输入有关)。 电路构成: ⚫ 存储电路(主要是触发器,必不可少) ⚫ 组合逻辑电路(可选)。 ⚫ 时序逻辑电路的状态是由存储电路来记忆 和表示的。 5.1概述
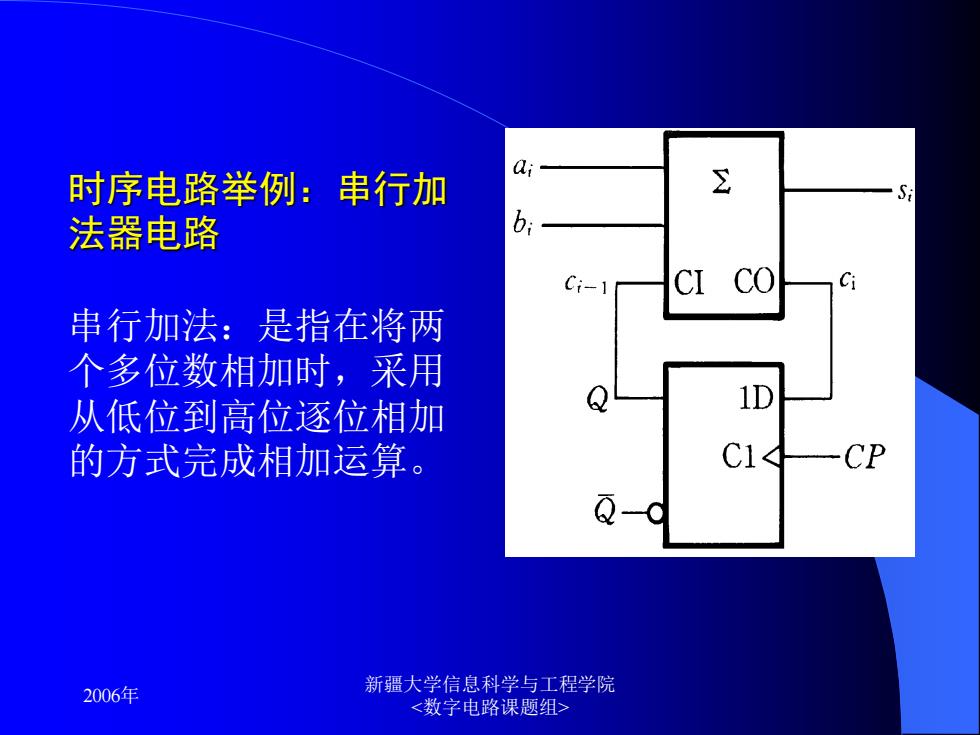
a 时序电路举例:串行加 Σ S 法器电路 Ci-1 co 串行加法:是指在将两 个多位数相加时,采用 从低位到高位逐位相加 的方式完成相加运算。 C1
2006年 新疆大学信息科学与工程学院 时序电路举例:串行加 法器电路 串行加法:是指在将两 个多位数相加时,采用 从低位到高位逐位相加 的方式完成相加运算
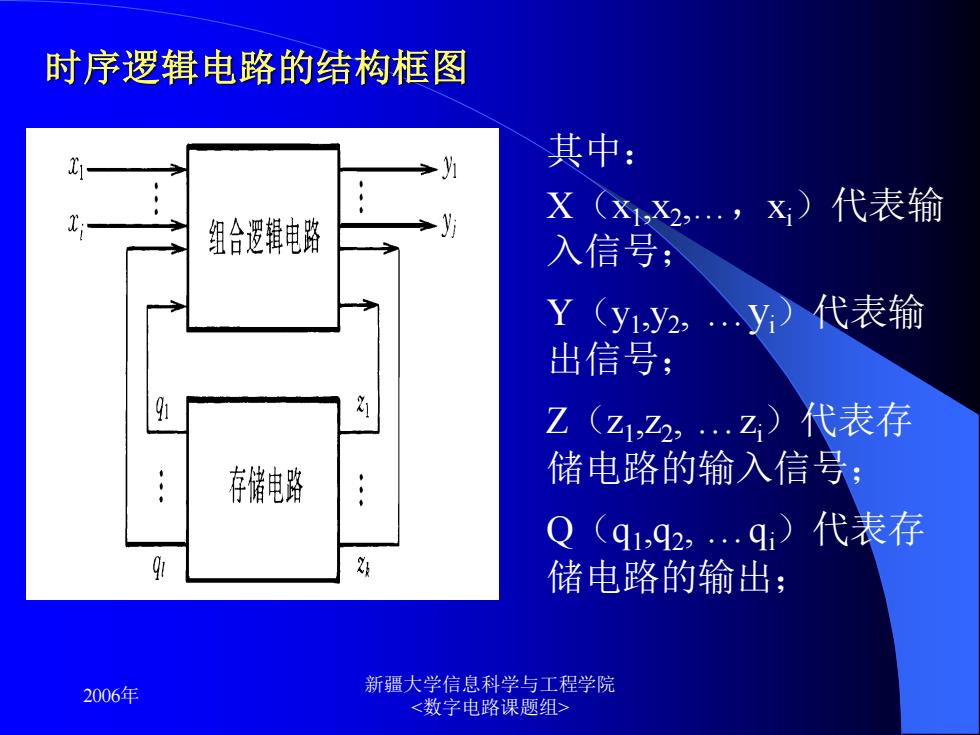
时序逻辑电路的结构框图 其中: 组合逻辑电路 XX1,2.,X)代表输 入信号; Y(y1y2,y)代表输 出信号: 21 Z(Z1乙2,.乙)代表存 存储电路 储电路的输入信号: Q(q1,92,.q)代表存 储电路的输出; 2006年 新疆大学信息科学与工程学院
2006年 新疆大学信息科学与工程学院 时序逻辑电路的结构框图 其中: X(x1 ,x2 ,.,xi)代表输 入信号; Y(y1 ,y2 , .yi)代表输 出信号; Z(z1 ,z2 , .zi)代表存 储电路的输入信号; Q(q1 ,q2 , .qi)代表存 储电路的输出;

y1=f1(x1,x2,.,x,q1,q2,.,q) y2=f2(x1,x2,.,x,q1,q2,.,91) (5.1.1) 输出方程 y,=f(x1,x2,.,x,q1,q2,.,q1) 之1=81(x1,x2,.,x;,q1,92,q1) z2=g2(x1,x2,.,x;,91,q2,.,91) (5.1.2) 驱动方程 之k=gk(x1,x2,.,x,q1,92,.,91) q1*1=h(之1,之2,.,之4,qi,q2,.,q) g2*1=h2(之1,x2,.,2,q1,92,.,9) (5.1.3) 状态方程 q”+1=,(1之2,.,之,q1,q2,.,9i) 写成向量函数形式,有: Y=F[X,Q] Z=G[X,Q] Q+1=H[Z,Q] 2006年 新疆大学信息科学与工程学院
2006年 新疆大学信息科学与工程学院 写成向量函数形式,有: Y=F[X,Q] Z=G[X,Q] Qn+1=H[Z,Qn]

5.2时序逻辑电路的分析方法 时序逻辑电路可分为:同步时序电路和异步时序电路。 5.2.1同步时序逻辑电路分析方法 1)从给定的逻辑图中写出每个触发器的驱动方程. 2)把得到的驱动方程代入响应触发器的特性方程, 得状态方程,从而得到整个电路的状态方程组· 3)根据逻辑图写出电路的输出方程. 2006年 新疆大学信息科学与工程学院 返圆目录
2006年 新疆大学信息科学与工程学院 时序逻辑电路可分为:同步时序电路和异步时序电路。 5.2.1 同步时序逻辑电路分析方法 1)从给定的逻辑图中写出每个触发器的驱动方程. 2)把得到的驱动方程代入响应触发器的特性方程, 得状态方程,从而得到整个电路的状态方程组. 3)根据逻辑图写出电路的输出方程. 5.2时序逻辑电路的分析方法
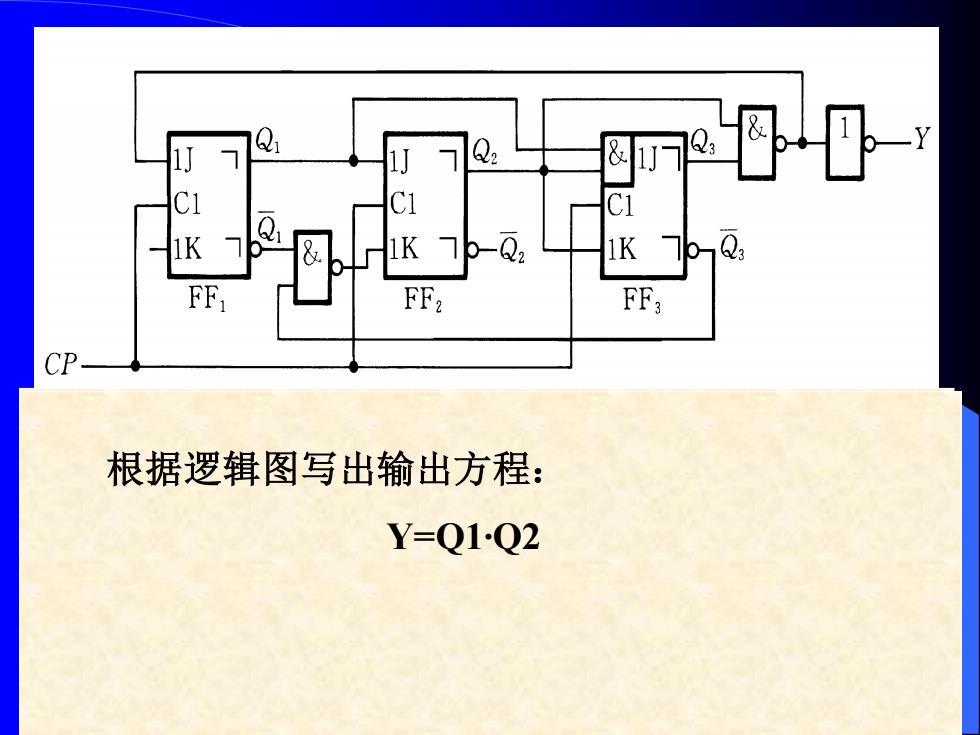
K FF FF FF: CP 根据逻辑图写出输出方程: Y=0102
2006年 新疆大学信息科学与工程学院 【例5.2.1 】 试分析下图时序逻辑电路的逻 辑功能,写出它的驱动方程,状态方程和输出方 程。 FF1 、FF2 和FF3 是三个主从结构的TTL触发 器,下降沿动作,输入端悬空时和逻辑1状态等效。 将驱动方程代入 由给定的逻辑图可写出驱动方程: JK触发器的特性方程,得到状态方程: 根据逻辑图写出输出方程: Y=Q1∙Q2

5.2.2时序逻辑电路的状态转换表,状 态转换图和时序图 一、状态转换表 →若将任何一组输入变量及电路初态的取值代入状态 方程和输出方程,即可算出电路的次态和现态下的 输出值; →以得到的次态做为新的初态,和这时的输入变量取 值一起再代入状态方程和输出方程进行计算,又得 到一组新的次态和输出值; 如此继续下去,把全部的计算结果列成真值表的形 式,就得到状态转换表. 2006年 新疆大学信息科学与工程学院
2006年 新疆大学信息科学与工程学院 5.2.2时序逻辑电路的状态转换表,状 态转换图和时序图 一、状态转换表 →若将任何一组输入变量及电路初态的取值代入状态 方程和输出方程,即可算出电路的次态和现态下的 输出值; →以得到的次态做为新的初态,和这时的输入变量取 值一起再代入状态方程和输出方程进行计算,又得 到一组新的次态和输出值; →如此继续下去,把全部的计算结果列成真值表的形 式,就得到状态转换表.
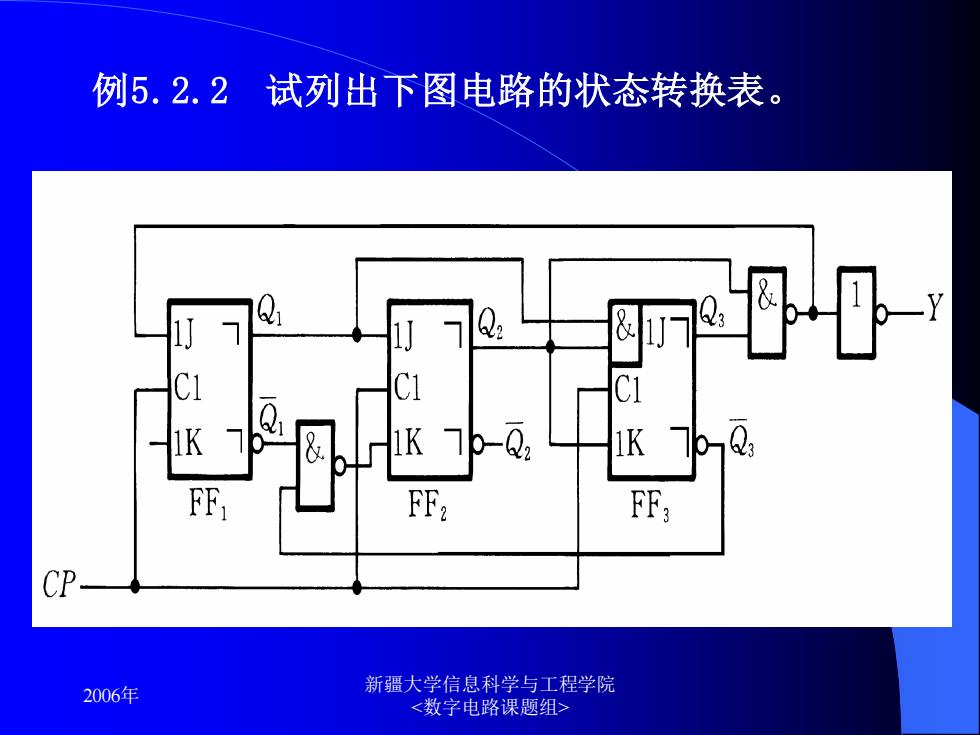
例5.2.2试列出下图电路的状态转换表。 Ci 风 ik 7-2 FF, FF: D 2006年 新疆大学信息科学与工程学院
2006年 新疆大学信息科学与工程学院 例5.2.2 试列出下图电路的状态转换表
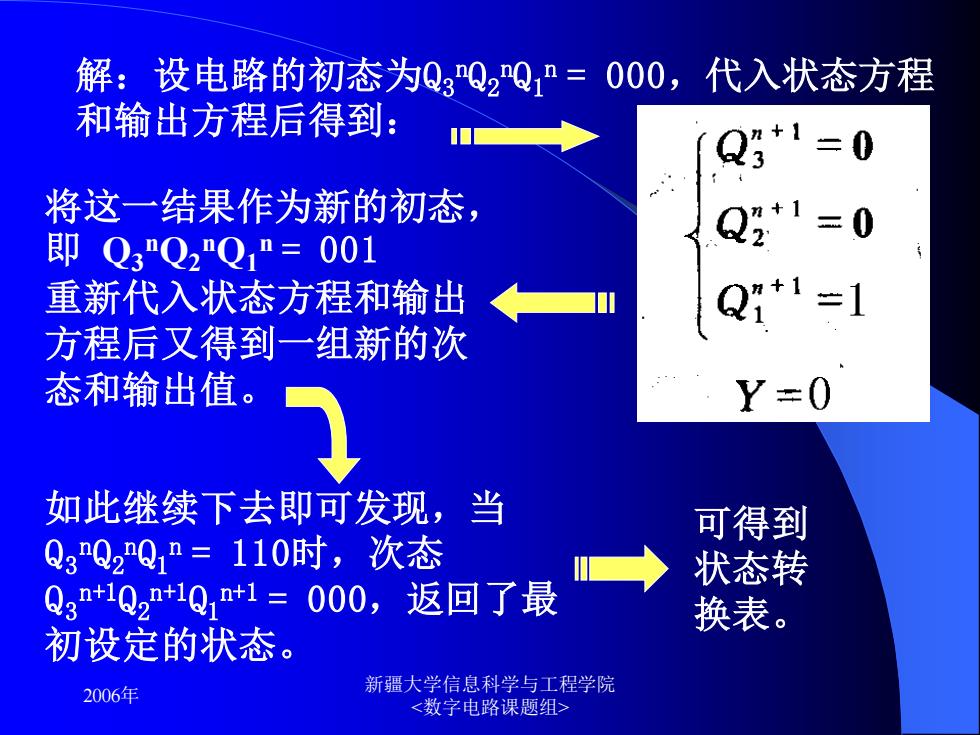
解:设电路的初态为QgQ2Qn=000,代入状态方程 和输出方程后得到: Qg*1=0 将这一结果作为新的初态, 即Q3Q2Q1"=001 Q经*1=0 重新代入状态方程和输出 Q1*1=1 方程后又得到一组新的次 态和输出值。 Y=0 如此继续下去即可发现,当 可得到 QgQ2Q1n=110时,次态 状态转 Qg+1Q2n+1Q1n+1=000,返回了最 换表。 初设定的状态。 2006年 新疆大学信息科学与工程学院 <数字电路课题组
2006年 新疆大学信息科学与工程学院 解:设电路的初态为Q3 nQ2 nQ1 n = 000,代入状态方程 和输出方程后得到: 将这一结果作为新的初态, 即 Q3 nQ2 nQ1 n = 001 重新代入状态方程和输出 方程后又得到一组新的次 态和输出值。 如此继续下去即可发现,当 Q3 nQ2 nQ1 n = 110时,次态 Q3 n+1Q2 n+1Q1 n+1 = 000,返回了最 初设定的状态。 可得到 状态转 换表