
第四章角动量理论
第四章 角动量理论

§4.1角动量算符的一般性质
§4.1 角动量算符的一般性质

角动量算符满足如下的对易关系 [,]=访,[,=hi,[,]= 我们定义总角动量算符 2三梁+记+2. 同时,我们还可以定义升和降算符为 J=Jr+ijy:1=Jr-iju
角动量算符满足如下的对易关系 我们定义总角动量算符 同时,我们还可以定义升和降算符为

不难验证,他们满足如下的对易关系 [J,J±]=±J生 JJ-JJ.=2hJ, J±J年=J2-J±h JJ+JJ+=2(J2-J2) 例如,我们有 [,j4]=[i,j+动=[i,+i[, =流jg+(-ihj)=h.jg+ijn=五j+. 以及 [,刘=,=[,刘=0
不难验证,他们满足如下的对易关系 以及 例如,我们有 2 2 , z z z J J J J J J J J = = − 2 2 2 2( ) z z J J J J J J J J J J J + − − + + − − + − = + = −

例如: [2,刘=[2++,]=[+,] 201+14,=5八1,+号1, 八,1+1,月+0,1+2,可 1+2,1+i1-机 0. 又由于在总角动量算符卫中,j2与方和是对称的,故 [户,=,=0 也必成立
例如:

由于卫和j是对易的,它们具有共同的本征态和本征值。即我们可以找 到{入,m)},使得 1入,m)=λh1入,m以,j入,m)=mh入,m) 同时成立。 为了得到本征值入和m的可能取值范围,我们首先考虑恒等式[户,j4]=0 的矩阵元 ,m'[,j4]入,m)=(X,m1pj-j4P入,m)=0

按照定义,我们有 (X,m12j4-j421入,m)=(X-)h(X,m'j+入,m). 因此,当'≠入时,我们有 (X,mJ+入,m〉=0. 也就是说 (,mJ+入,m)=xx(A,mJ+,m》 成立。 把J换成Jx、J会是什么结果?
x y z , , J J J 把 +换成 、 -会是什么结果?
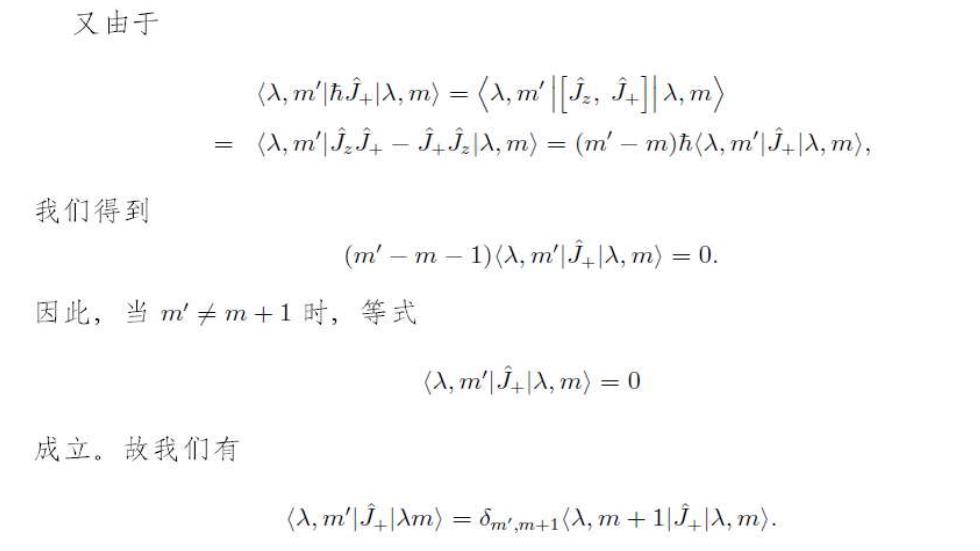
又由于 ,mhj4入,m)=(,ml[i,4]入,m〉 =(,mjj-j4j入,m)=(m'-m)(入,m1j|λ,m, 我们得到 (m'-m-1)(入,m1j入,m)=0. 因此,当m≠m+1时,等式 (,m1j4入,m)=0 成立。故我们有 (入,m'1j+Am)=dm,m+1A,m+1j4入,m)

同理,利用对易关系[,]=-,我们可得 (入,m1j_|Am)=6m,m-1(入,m-1j-|入,m. 为了求得(公,m+1j入,m)和(公,m-1j入,m)的非零值,我们可以利用恒 等式 2山41+14)=2+乃-户-2

由此,我们得到 12 入,m方+j+方_方+入,m》 2 ∑∑,m4X,m)(X,m1IA,m 2 ∑∑入,m)|X,m,m1j+,m) (A.mlj:1A.m-1)4.m-1-.m) 2入,m入,m+1)以,m+1+入,m) 入方2-m2h2=(入-m2)2